はじめに
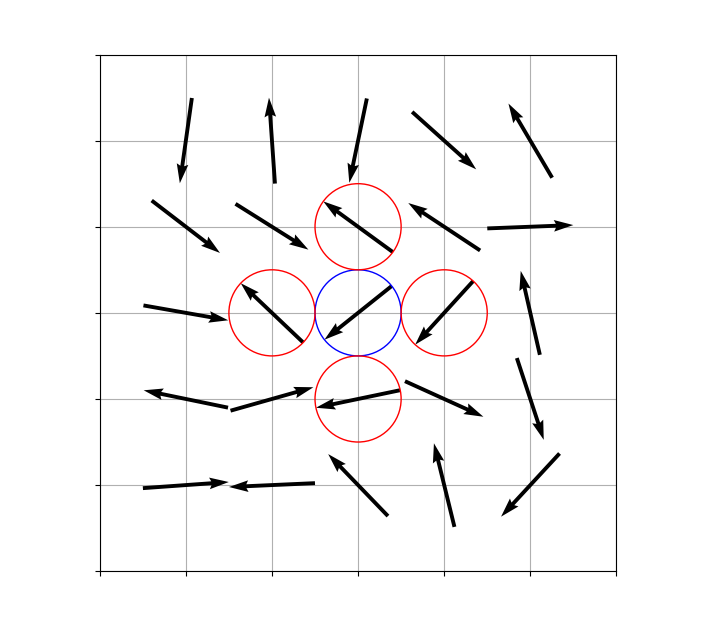
本記事では正方格子上の2次元XYモデルについてメトロポリス法によるモンテカルロシミュレーションを行います。
このモデルはKT転移(コステリッツ=サウレス転移)という特殊な相転移(トポロジカル相転移)を起こすことで有名で、2016年にノーベル物理学賞に選ばれています。
イジングモデルのシミュレーションの記事は豊富にありますが、XYモデルのシミュレーションの記事は殆ど見られなかったので備忘録も兼ねて執筆したいと思います。
2次元XYモデル
2次元XYモデルとは、スピン変数を2成分のベクトルとしたものである。スピンは2次元の単位ベクトルであり、格子点上に配置される。
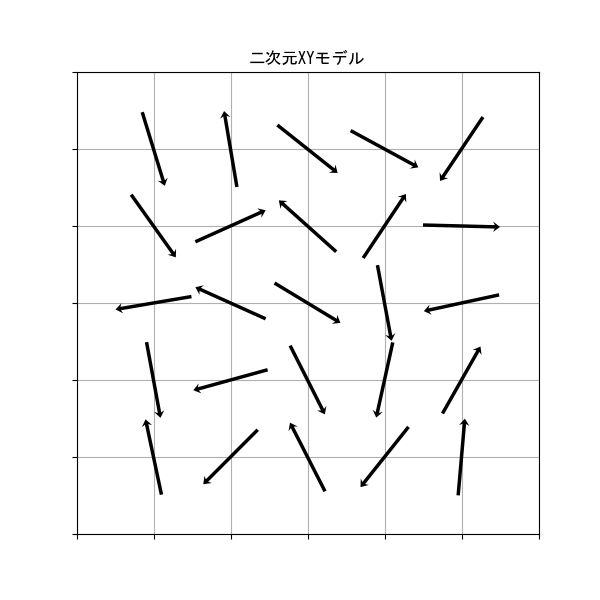
エネルギー
2次元正方格子上のXYモデルのエネルギーは以下で与えられる。
$$H =-J\sum_{<i,j>}\boldsymbol{S_i}・\boldsymbol{S_j}=-J\sum_{<i,j>}\cos(θ_i-θ_j)$$
ここで<i,j>は最近接のスピンを表します。
Jは相互作用結合定数です。
メトロポリス法によるモンテカルロシミュレーション
詳しい理論は参考をご覧ください。ここではアルゴリズムの内容のみ説明します。
1)スピン$\boldsymbol{S_{ij}}$の角度$\boldsymbol{θ_{ij}}$に乱数を足し合わせた場合を考える。
2-1)その際、エネルギー変化が負の場合には角度を変更する。
2-2)エネルギー変化が正の場合には遷移確率に従って角度を変更する。
3)平衡状態に達するまで十分回数繰り返す
$$遷移確率:P_{tr} = exp(ΔE/T)$$
初期条件
・格子数 Nx,Ny = 30,45,60
・相互作用結合定数 J = -1
・ボルツマン定数 Kb = 1
・モンテカルロステップ数 steps
・熱平均の為のサンプル数 avsteps = 0.2×steps
(0.8steps以降にて熱平均を取った)
コーディング
Python3.8.2使用
numbaのjitclassを用いて高速化しています。
(なんらかの高速化なしだと1~2時間かかると思います。。。)
import random
import numpy as np
import matplotlib.pyplot as plt
import numba
from numba import jit, f8, i4
from numba.experimental import jitclass
spec = [
("Nx", i4),
("Ny",i4),
("J",f8),
("steps",i4),
("state",f8[:,:]),
("KBT",f8)
]
@jitclass(spec)
class XYmodelMetropolisSimulation:
#コンストラクタ
def __init__(self,Nx,Ny,J,steps,KBT):
self.KBT = KBT
self.Nx = Nx
self.Ny = Ny
#スピン結合定数 1:強磁性 or -1:反強磁性
self.J = J
#初期状態の作成
self.state = np.random.uniform(0,2*np.pi,(self.Nx,self.Ny))
self.steps = steps
#周期的境界条件の導入
def is_boundary(self,i,j):
i = (i + self.Nx) % self.Nx
j = (j + self.Ny) % self.Ny
return i,j
#エネルギーの計算
def calc_energy(self):
E = 0
for i in range(self.Nx):
for j in range(self.Ny):
E += self.J*( np.cos(self.state[i,j]-self.state[self.is_boundary(i+1,j)])+np.cos(self.state[i,j]-self.state[self.is_boundary(i,j+1)]) + \
np.cos(self.state[i,j]-self.state[self.is_boundary(i-1,j)])+np.cos(self.state[i,j]-self.state[self.is_boundary(i,j-1)]) )
return E
#角度を0~2πにする
##lambda使うとエラー出た→G_list = list(map(lambda x: x/(self.Nx*self.Ny*self.Nx/2),G_list))
def normalize_angle(self):
for i in range(self.Nx):
for j in range(self.Ny):
self.state[i,j] = self.state[i,j] % (2*np.pi)
return self.state
#相関関数の計算
def calc_correlation_func(self,state):
G_list = []
for r in range(1,int(self.Nx/2)):
G = 0
for i in range(self.Nx):
for j in range(self.Ny):
#周期的境界条件含んでいるからN/2までで大丈夫
G += np.cos(state[i,j]-state[self.is_boundary(i+r,j)]) + np.cos(state[i,j]-state[self.is_boundary(i-r,j)]) + \
np.cos(state[i,j]-state[self.is_boundary(i,j+r)]) + np.cos(state[i,j]-state[self.is_boundary(i,j-r)])
G_list.append(G/(self.Nx*self.Ny))
return G_list
#メインコード(メトロポリス法によるモンテカルロシミュレーション)
def montecarlo(self):
state_list = []
E = self.calc_energy()
delta_E = 0
E_total = 0
E2_total = 0
for count in range(self.steps):
for i in range(self.Nx):
for j in range(self.Ny):
alpha = random.uniform(0,2*np.pi)
delta_E = -2*self.J*np.cos(self.state[i,j]-alpha)*(np.cos(alpha-self.state[self.is_boundary(i+1,j)])+ \
np.cos(alpha-self.state[self.is_boundary(i,j+1)])+np.cos(alpha-self.state[self.is_boundary(i-1,j)])+np.cos(alpha-self.state[self.is_boundary(i,j-1)]))
state_trial=self.state.copy()
state_trial[i,j]= np.pi - self.state[i,j] + 2*alpha
E_trial =E + delta_E
#メトロポリス法による状態更新
if E_trial <= E :
self.state = state_trial
E = E_trial
else :
if random.random() < np.exp(-delta_E/self.KBT): #遷移確率にて変更
self.state = state_trial
E = E_trial
#熱平均を取る
if count >= 0.75*self.steps:
#角度を0~2πにする
self.state = self.normalize_angle()
state_list.append(self.state)
E_total += (E/(self.Nx*self.Ny))
E2_total += (E/(self.Nx*self.Ny))**2
E_avg = E_total / (0.25*self.steps) #エネルギーの熱平均
E2_avg = E2_total / (0.25*self.steps) #エネルギーの2乗の熱平均
#比熱は系全体
cv_avg = (self.Nx*self.Ny)*(E2_avg - E_avg**2)/self.KBT**2
return state_list,E_avg,cv_avg
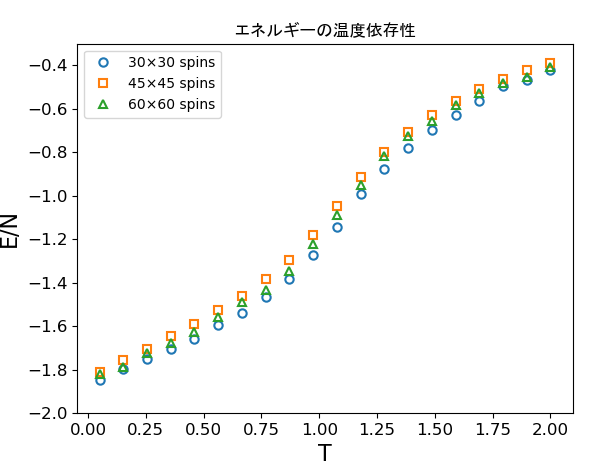
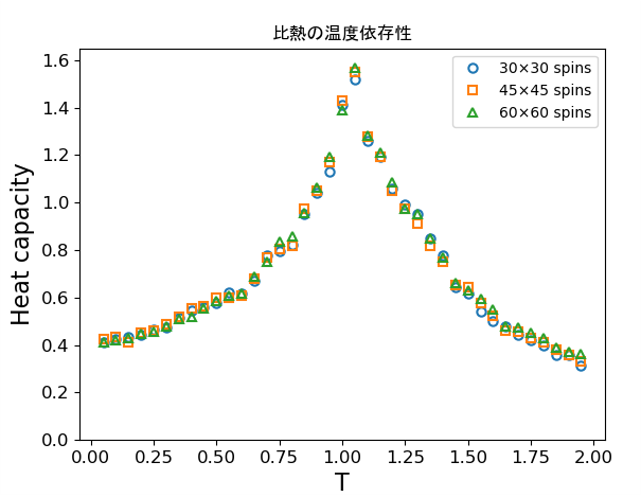
計算結果:エネルギー・比熱の温度依存性
計算結果:相関関数
XYモデルにおいて、スピン${\boldsymbol{S_i},\boldsymbol{S_j}}$についての相関関数は以下で定義される。
$$G(\boldsymbol{{r_i}-{r_j}}) ={<\boldsymbol{S_i}・\boldsymbol{S_j}>}={<\cos({θ_i}-{θ_j})>}$$
以下のグラフは距離r離れたスピンとの相関関数のグラフである。(周期的境界条件を導入しているのでξ/2で対称となっています。)
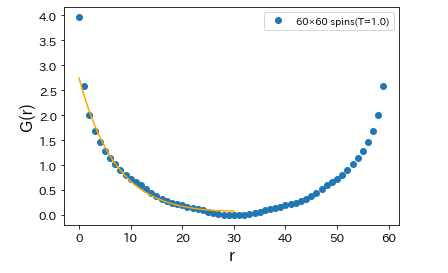
相関関数を高温領域において周期的境界条件を含めると、
$$G(\boldsymbol{{r_i}-{r_j}}) ∝ (e^{-r/ξ} + e^{-(L-r)/ξ}) $$となる。ξは相関長である。
上式より指数フィッティングする事で相関長ξを求める事ができる。
相関関数のフィッティングコード
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
def func1(X,a,b,r,c):
Y = a * (np.exp(-b*X/r) + (np.exp(-(b-c)*X/r))
return Y
# 対称なのでξ/2まででOK
x_data = [i for i in range(30)]
y_data = G60[:30]
popt, pcov = curve_fit(func1,x_data,y_data)
print(popt)
r_list = [i for i in range(60)]
plt.plot(r_list,G60[:60],marker='o',linestyle='none',label='60×60 spins(T=1.0)')
x = np.linspace(0,30,100)
plt.plot(x,func1(x,popt[0],popt[1],popt[2],popt[3]),color='orange')
plt.legend()
plt.tick_params(labelsize=12)
plt.xlabel("r",fontsize=16)
plt.ylabel("G(r)",fontsize=16)
plt.show()
相関長と温度の関係
フィッティングによって得られた各温度での相関長のグラフが以下になる。
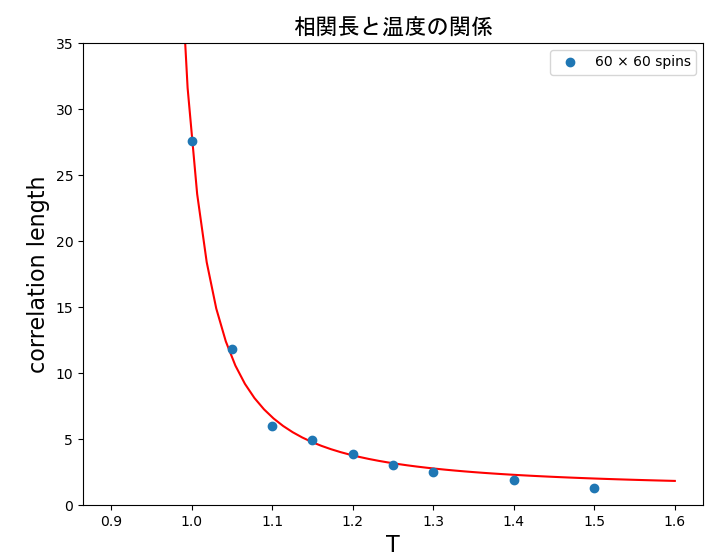
ここでは、exp(a/(x-b))の形で指数フィッティングを行った。
これより相関長が発散する温度、つまり転移温度$T_c$=0.87が求まる。
補足1)比熱の計算式
統計力学において比熱は次式で与えられる。
$$C_V = \frac{<E^2> - <E>^2}{K_BT^2}$$
<E^2>はエネルギーの2乗の平均を、<E>^2はエネルギーの平均の2乗を表します。
補足2)周期的境界条件
def is_boundary(self,i,j):
i = (i + self.Nx) % self.Nx
j = (j + self.Ny) % self.Ny
return i,j
周期的境界条件:${\boldsymbol{S_{i+L}}=\boldsymbol{S_i}}$($L$は格子長)
%を用いる事で簡潔に表現できます。
まとめ
比熱のピークと転移温度は一致しなかった。トポロジカルな渦が発生している事が原因だと思われます。
時間ができたら渦のカウント方法や温度依存性も追記しようと思います。
参考文献・サイト
- Jan Tobochnik and G. V. Chester:Monte Carlo study of the planar spin model(1979)
- Qiita記事[Pythonによる科学・技術計算] 2次元イジングスピン系の熱力学量のメトロポリス法によるモンテカルロシミュレーション