はじめに
モンテカルロ法の統計力学への応用としてイジングモデルを用いたスピン磁性のシミュレーションがよく行われている。本稿では2次元イジングモデルのモンテカルロシミュレーションをPythonを用いて行う。
理論・手法の概略は補遺にまとめたので興味がある方は参考にしてください。。
内容
$N_x \times N_y$格子上の2次元系イジングモデルのハミルトニアンは以下で与えられる[1,2]。
$H=-J \ \sum_{i=1,\ldots,N_x} \sum_{j=1,\ldots,N_y} s_{i,j}\ s_{i,i+1} - h \sum_i s_i$ $\tag{1}$
第一項がスピン-スピン相互作用(交換相互作用),第二項が磁場との相互作用(ゼーマン相互作用)をそれぞれ示している。
$J$はスピン-スピン相互作用結合定数であり,系の磁性的性質を特徴付けるうえで重要なパラメータである。$J \gt 0$で強磁性的, $J \lt 0$が反磁性的な相互作用を記述する。
ここで$(i,j)$は二次元格子上の点の指標で,和は最近接対相互作用を考えている。$s_{i,j}$は,$s_{i,j}=1$(アップスピン)または$s_{i,j}=-1$(ダウンスピン)をとる。$h$は外部磁場である。
本稿ではこの2次元イジングスピン系の熱エネルギー・磁化・比熱の温度依存性をメトロポリス法によるモンテカルロシミュレーションによる決定を目的とする。
[計算条件]
シミュレーションでは$20 \times 20$のグリッドを用い,$J=1$および $h=0$とした。
モンテカルロステップの総数を40000, 熱平近値計算のためのサンプリング数をおよそ8000とした(モンテカルロステップが32000くらいから平均をとった)。
また,境界にいるスピンのスピン-スピン相互作用は周期境界条件を用いて評価した。
計算コード
Python3.5.1使用。
Jupyter notebook 5.0.0上で実装・動作確認を行った。
"""
2次元イジングモデルのメトロポリス法によるモンテカルロシミュレーション
"""
from random import random, randrange
import numpy as np
import matplotlib.pyplot as plt
# 与えられたスピン配置alisに対してエネルギーを計算する関数を定義
def Ecalc2(alis2, Nx,Ny):
dum=0
for i in range(-1,Nx):
for j in range(0,Ny):
l=i
m=j
if l==-1:
l=Nx
if l == Nx:
l=0
if m ==-1:
m=Ny
if m== Ny:
m=0
ll=i+1
if ll == Nx:
ll=0
dum+=alis2[l, m]*alis2[ll, m]
for i in range(0,Nx):
for j in range(-1,Ny):
l=i
m=j
if l==-1:
l=Nx
if l == Nx:
l=0
if m ==-1:
m=Ny
if m== Ny:
m=0
mm=j+1
if mm == Ny:
mm=0
dum+=alis2[l, m]*alis2[l, mm]
return dum
# ランダムな初期状態生成: アップスピン数とダウンスピン数は同じ。M=0
def Initial_rand(s, Nx,Ny):
NN=int(Nx*Ny/2)
for k in range(NN):
i=randrange(Nx-1) # 1からNまででランダムな数が選ばれる
j=randrange(Ny-1) # 1からNまででランダムな数が選ばれる
s[i,j]=-1*s[i,j]
return s
Nx= 20 # x方向に100分割
Ny =20 # y方向に100分割
Ntot=Nx*Ny
KBT_lis=np.linspace(0.001,6, 201) # 温度を0.001から6まで(kBT単位で)201刻みで変動させる。
ETplot=[]
MTplot=[]
CTplot=[]
for KBT in KBT_lis:
J = 1 # スピン結合定数
B = 0.0 # 外部磁場
steps =40000 # MC ステップ
avsteps=int(steps/5)
# 初期状態生成: ランダムスピン配置
s= np.ones([Nx,Ny], int) # Nスピン分の, 量子数(Sz = +1 or -1)を全部1としてセット
s=Initial_rand(s, Nx,Ny)
E = -J* Ecalc2(s, Nx,Ny) -B*np.sum(s) #(初期)エネルギーを計算。
E2 = E**2 # E^2を格納
# セットアップ
eplot = [] #各温度kBTの下でエネルギー値を格納するためのリストを定義
Eavplot=[] #エネルギーの熱平均値を格納するためのリストを定義
e2plot = []#各温度kBTの下でエネルギー値の二乗を格納するためのリストを定義。比熱の計算で使う。
eplot.append(E/Ntot)
Eavplot.append(E/Ntot)
e2plot.append((E/Ntot)**2)
Cvplot = [] ##各温度kBTの下で比熱を格納するためのリストを定義
M = np.sum(s) # 磁化の計算
Mplot = []
Mavplot=[]
Mplot.append(M/Ntot) # 磁化の熱平均値
Mavplot.append(M/Ntot) #磁化の熱平均値を格納するためのリストを定義
# メイン
for k in range(steps):
i=randrange(Nx-1) # 0からN-1まででランダムな数が選ばれる
j=randrange(Ny-1) # 0からN-1まででランダムな数が選ばれる
s_trial=s.copy()
s_trial[i,j]= -1*s[i,j]
delta_E=2*s_trial[i,j]*-1*J*(s[i+1,j]+s[i-1,j]+s[i,j+1]+s[i,j-1])-B*(s_trial[i,j]-s[i,j])
E_trial =E+ delta_E
#メトロポリス法による状態更新
if E_trial < E :
s = s_trial
E = E_trial
else :
if random() < np.exp(-(delta_E)/KBT):
s = s_trial
E = E_trial
eplot.append(E/Ntot)
e2plot.append((E/Ntot)**2)
M = np.sum(s)
Mplot.append(M/Ntot)
ETplot.append(np.sum(eplot[-avsteps:])/avsteps)
MTplot.append(np.sum(Mplot[-avsteps:])/avsteps)
CTplot.append((np.sum(e2plot[-avsteps:])/avsteps-((np.sum(eplot[-avsteps:]))/avsteps)**2)/KBT**2) #比熱の計算
plt.plot(KBT_lis,ETplot)
plt.ylabel("Totla energy per spin")
plt.xlabel("kBT")
plt.show()
plt.plot(KBT_lis,MTplot)
plt.ylabel("Total magnetic moment per spin")
plt.hlines([0], 0, KBT_lis[-1], linestyles="-") # y=0に線を描く。
plt.xlabel("kBT")
plt.show()
plt.plot(KBT_lis,CTplot)
plt.ylabel("Heat capacity per spin")
plt.xlabel("kBT")
plt.show()
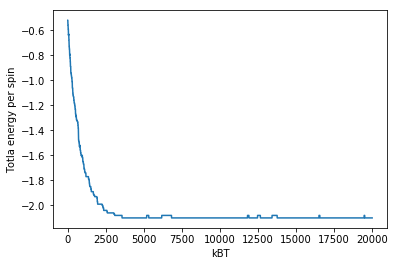
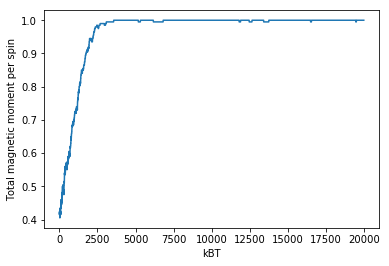
結果(1)エネルギー・磁化の時間発展
等温下のモンテカルロシミュレーション中に物量がモンテカルロステップとともに変化する様子の一例を以下に示す。これは計算コードから直接得られない。表示するには,計算コード中の温度のループ(for KBT in KBT_lis: というところ)をせず以下のプロット文を書けば良い。
plt.plot(eplot)
plt.ylabel("Totla energy per spin")
plt.xlabel("kBT")
plt.show()
plt.plot(Mplot)
plt.ylabel("Total magnetic moment per spin")
# plt.hlines([0], 0, steps, linestyles="-") # y=0に線を描く。
plt.xlabel("kBT")
plt.show()
$k_BT=1$とした。ステップ数の増加に伴い物理が収束していく様子(熱平衡状態に到達していく様子)がみられる。
結果(2) 温度依存性
以下,シミュレーションによって得られた図を示す。さらに高精度の結果を得たいのなら,シミュレーションの格子グリッド数をより増加させると良い。
強磁性から常磁性への相転移温度,$T_c$の理論値は,$T_c=2.2691$[補遺(4-1)式(12)を参照]である。
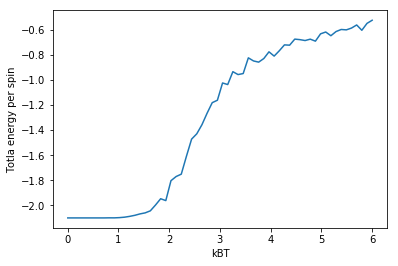
スピンあたりの全エネルギー。高温になるにつれスピンが反対向きのペアが生じるためエネルギーが増加する。
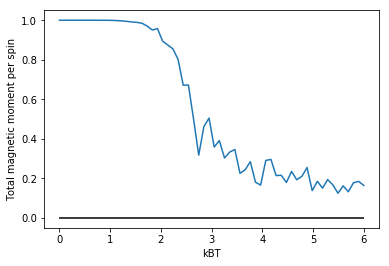
磁化の温度依存性。加温に伴い磁化が消失する(強磁性体から常磁性体への相転移)。図ではわかりにくいが,厳密には,$T=T_c$で不連続に変化する(二次の相転移)である。
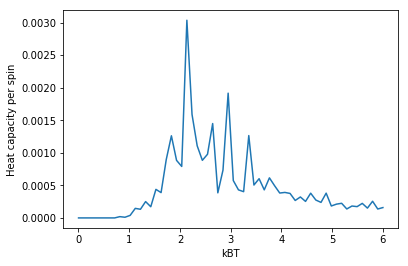
比熱の温度依存性。磁性転移は二次の相転移であり,$T=T_c$で比熱が発散する。この図からもその傾向が見られる。
補遺
補遺(0): スピン状態の時間発展
シミュレーション中にスピン状態の変化を以下にアニメーションで示す。初期スピン状態は全て上向き(アップスピン,$s_{i,j}=1$)とし,$k_BT=30$とした。この温度では常磁性状態が安定となり,上向きと下向きのスピンが同程度になるようにスピン状態が変化していく様子が示される。
100x100グリッドのスピン状態の変化。ピンクがアップスピン($s_{i,j}=1$),水色がダウンスピン($s_{i,j}=-1$)を表す。時間変化によってダウンスピンが増加していく。
補遺(1):理論
量子統計力学によれば温度Tの熱平衡状態において物理量(オブザーバブル演算子)$\hat A$の熱平均値$< A>$は,系のハミルトン演算子を$\hat H$とすると,
$< A> = Tr (\hat ρ \hat A) = e^{-\beta \hat H \hat A} /Z \tag{2}$
で与えられる。ここでTrは対角和,$\beta = 1/(k_B T) $は逆温度などと呼ばれる量である。
$\hat ρ$は密度行列演算子であり,熱平衡状態では
$\hat ρ = e^{-\beta \hat H} /Z \tag{3}$
となることを用いた。
$\hat H$と$\hat A$を同時に対角化する表示を用いると対角和は,
$< A> =\sum_{i=1}^{n} A_i \exp({ -\beta E_{i} }), \ \ \ Z =\sum_{i=1}^{n} \exp({ -\beta E_{i} })\tag{4}$
とかける。$ E_{i}$は$\hat H$の$i$番目のエネルギー固有値で,$Z$は分配関数である。
補遺(2): メトロポリス法によるモンテカルロシミュレーション
補遺(1)により有限温度下における物理量の熱平均値が理論的に記述できることが分かった。この理論体系は理論物理学における金字塔の一つであろう。しかし,実際に計算するという立場からすると,熱平均値の計算を行うことは一般に極めて困難である。理由は,シュレディンガ-方程式の解の数(状態数)が莫大となることがしばしばあり,すべての状態についての和を取れないためである。
そこで,乱数を使って適当な状態を複数サンプリングし,それらの平均として$< A>$を近似的に求めることが行われる(モンテカルロシミュレーション)。
サンプル数をNとすると, そのようにして求まった$< A_N >_{MC}$は, 以下の条件(1)と(2)を満たすとき,Nが無限大になるとともに全ての対角和を厳密に計算した$< A>$へと漸近することが知られている。そのため,十分大きなNをとれば物理量の熱平均値を精度良く求めることが可能である。
$\lim_{N\to\infty} < A_N >_{MC} = < A> \tag{5}$
条件
(1): モンテカルロシミュレーションがエルゴード的であること
(2): 「詳細釣り合いの条件」を満たすこと
(1)は,任意の初期状態から出発し時間発展とともに系の状態が移り変わるが,考えられるすべての状態を経ることができる,というものである(エルゴード条件)。
(2)は,熱平衡状態で状態$i$が実現する確率$\pi(i)$,状態$i$から状態$j$へと移る確率(遷移確率)を$w(i,j)$とするときに,
$\pi(i)\ w(i,j)=\pi(j) \ w(j,i)$
を満たすことである。
$w(i,j)$の選び方は任意性がある。メトロポリス法では状態iから状態jへの遷移確率$w(i,j)$を以下のように設定する。
$w(i,j) =$$ 1 (E_j \le E_i)\ $, $ \ e^{-\beta \ (E_j-E_i)} \ (E_j > E_i) \tag{6}$
これによって種々の状態を次々に作り出し,十分時間が経つと系の取り得る状態は統計力学におけるカノニカル集団に対するボルツマン分布に従うようになることが証明されている[4]。メトロポリス法による$w(i,j)$の選び方はしたがって統計力学と親和性が高く,計算統計物理学で必要不可欠なものとなっている。
補遺(3): イジングモデルのメトロポリス法によるモンテカルロシミュレーションの手順
- 任意のスピン配列$A_k$を作る
- 新しいスピン配置$A_{k+1}$を発生するために,ランダムにi番目のスピンをとりあげる
- 試行配置をつくるためにスピンiのスピン方向を反転させ(スピンフリップ)た状態$A_{trial}をつくり,$エネルギー$E_{tri}$を計算する
- もし$E_i \ \le E_{trial}$ ならその試行配置を受け入れる($A_{k+1}$=$A_{trial})$
5.もし$E_i \ \gt E_{trial}$ なら確率$P_{tr}=exp[-(\beta \ (E_{trial}-E_i))]$で受け入れる($A_{k+1}$=$A_{trial}$)
ここで5は,
5-1. 一様乱数 $r$ $(0\le r \le 1)$を発生する
5-2. $r$ と$P_{tr}$の大小関係を比較し,$P_{tr} \ge r$ならば$A_{k+1}$=$A_{trial}$,そうでない場合は状態変化を棄却する(($A_{k+1}$=$A_k$))
とする。
6. 物理量があまりかわらなくなくなるまで(熱平衡状態に達するまで)上の1-5までを繰り返す。エネルギーE, 磁化M, (等積)比熱Cvはそれぞれ,
$E= -J \ \sum_{i=1}^{n} s_i s_{i+1}\tag{7}$
$M= -J \ \sum_{i=1}^{n} s_i \tag{8}$
$C_v =\frac{E^2-<E>^2}{k_B T^2}\tag{9} $
であたえられる。$n$は粒子数である。
7. 熱平衡状態になってから複数ステップで物理量の平均を計算する。何ステップとるかは温度や粒子数によるが,高温であるほど多めのステップが必要かもしれない(エネルギーゆらぎが大きくなるため)。
補遺(4): その他
補遺(4-1) 2次元イジングモデルの厳密解
磁場無し(h=0)2次元イジングモデルには厳密解がある。
式(1)で与えられる2次元ハミルトニアンに対し,格子点数を大きくしていったときのエネルギーE,比熱Cv,磁化Mの漸近解はそれぞれ以下のようになる[3]。
$\frac{E}{N}=-J\ coth(j)\ [1+\frac{2}{\pi}\kappa'\ K(\kappa)] \tag{10}$
$\frac{Cv}{Nk_B}=\frac{1}{\pi} \frac{j}{sinh(j)}[2K(\kappa)-\frac{2}{\pi}-cosh^2(j) \ E(\kappa)+\kappa' sinh^2(j)\ K(\kappa)]\tag{11}$
磁化Mは $T \lt T_c(=\frac{J}{0.4407 \ k_B})$で,
$M=[\frac{cosh^2(j)}{sinh^4(j)}\ (sinh^2j-1)]^{\frac{1}{8}} \tag{12}$
であり, $T \gt T_c$では$M=0$である。
**この$T_c$こそが強磁性から常磁性への相転移温度であり,2次元イジングモデルが磁性相転移を記述できることを端的に表している。**なお,一次元では$M$は連続関数であり磁性転移は存在しない(同じことだが,$T_c$=0K$と記述されることもある)。
ここでj, $\kappa$, $\kappa'$はそれぞれ
$j=\frac{2J}{k_BT}$, $\kappa=2\frac{sinh(j)}{cosh^2(j)}$, $\kappa'=2\frac{sinh^2(j)-1}{cosh^2(j)}$ $\tag{13}$
で与えられる。
また,$K(\kappa)$と$E(\kappa')$はそれぞれ第一種および第二種完全楕円積分
${K(\kappa)=\int_0^{\pi/2}{\frac{1}{\sqrt{1-k^2\sin^2\theta}}}d\theta}\tag{13}$
${E(k)=\int_0^{\pi/2}{\sqrt{1-k^2\sin^2\theta}}d\theta}\tag{14}$
である(Pythonでの計算は[5]を参照されたい)。
補遺(4-2) 物質の磁性
電子の持つ量子力学的自由度の一つである"スピン"の振る舞いにあり, スピンとスピン同士の競合(スピン-スピン相互作用)の結果生じたものである。したがって磁石の本質を理解するには量子力学が必要である[1]。支配方程式は(非相対論的極限で)シュレディンガー方程式である。したがって, (A) 物質の磁性をシミュレートするには,スピン-スピン相互作用を考慮したシュレディンガー方程式を解く必要がある。
有限温度下における物質の熱力学的性質を扱う学問が統計力学である。それによれば,有限温度下における磁性についての定量的な情報は, (B)多くのスピンが存在する(多体)シュレディンガー方程式の解をすべて知り,ある重みを付けて平均を取ることで得られる。
残念ながら(A)と(B)を行うことは極めて困難である。以下の3点が主な理由である。
(C) スピン-スピン相互作用の実体は電子の統計性に由来した交換相互作用と呼ばれるものであり,このい相互作用のあらわな関数形が知られていない,
(D)たとえ相互作用の関数形が分かっているとしても多体シュレディンガー方程式を解くことが難しい
(E)たとえシュレディンガー方程式が解けたとしても熱統計平均値を得るための計算(分配関数等の計算)が大変難しい
ためである。
そのため,磁性の研究では,(C)と(D)に対しては,モデル相互作用(モデルハミルトニアン)を設定し それを考慮したシュレディンガー方程式を数値計算によって解き(E)に対しては本稿で取り扱ったような効率的なサンプリングを行うことで計算量を減らす,ということが古くからしばしば行われている。
多体相互作用(電子相関)による相転移を記述することは現在でも極めて挑戦的な課題である。イジングモデルおよびそれを量子力学的に取り扱うハイゼンベルグモデル(2次元XYモデル)などは(量子)モンテカルロ法と共に磁性体の熱力学(相転移等)を議論するうえで重要な役割を果たしてきた[2]。
参考文献
-
芳田奎, 「磁性」,岩波出版,1991.
-
宮下精二, 「熱・統計力学」,培風館,1993.
-
森田章・岡部豊,「シミュレーション統計物理」,丸善株式会社,1996.
-
kaityo256氏によるQiitaの記事「モンテカルロ法における詳細釣り合い条件と遷移確率の決め方について」は大変分かりやすく書かれており参考になった。オススメ。
-
Qiita記事「[Pythonによる科学・技術計算]scipy利用による物理学で使われる(特殊)関数の利用法リスト」にPythonによる完全楕円積分の計算について書いている。
追記
2017年8月12日
kaityo256氏から以下の貴重なコメントをいただいた。参考になります。ありがとうございました。
"なお、ご存知かも知れませんが、スピン系のモンテカルロシミュレーションは、Swendsen-WangやWolffアルゴリズムといったクラスターアップデートの方法を使うのが一般的です。シングルスピンフリップに比べて超強力な方法な方法です。Swendsen-Wangについては簡単な記事を書きましたので参考になれば幸いです。