この記事の目的
-
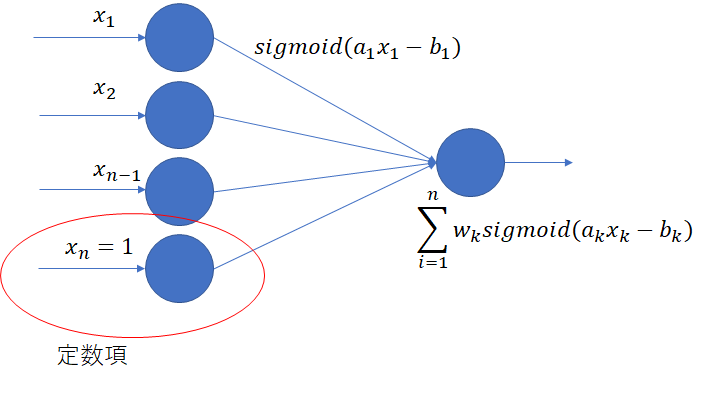
こちらの記事で非線形2層パーセプトロンについて書いた
-
2層パーセプトロンにおいてシグモイド関数のゲインと切片の両方を学習するとどうなるかを実験してみる
- すなわちsigmoid(ax-b)= 1/(1+exp(-ax+b))のaを前回は学習したがbも学習する
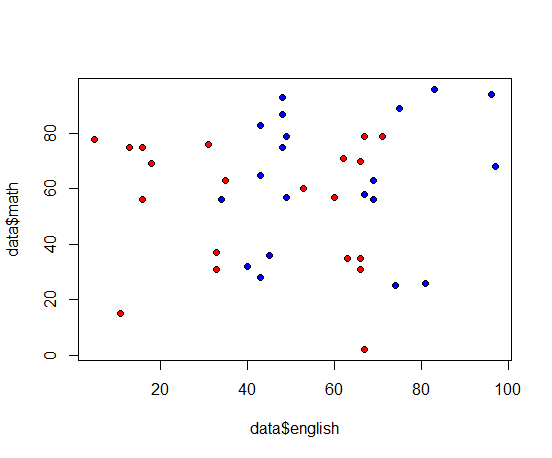
実験データ
- 前回と同じ
- 模試の数学と英語の点数で赤が不合格
学習方法
- 前回同様単純にbで二乗誤差を偏微分した値に小さい定数を掛け算して減算する
- より探索が必要となるため、学習回数は10倍にした
- 今回は定数を出力するニューロンはなくした
実験結果
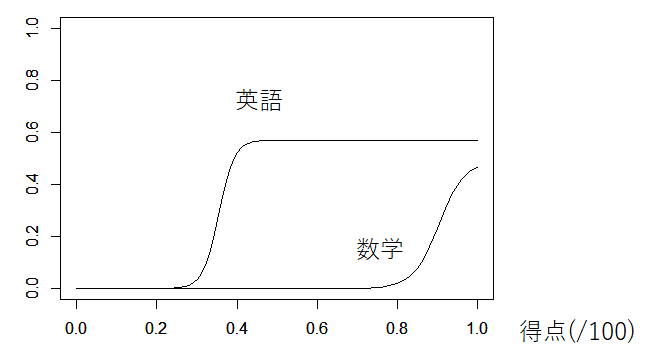
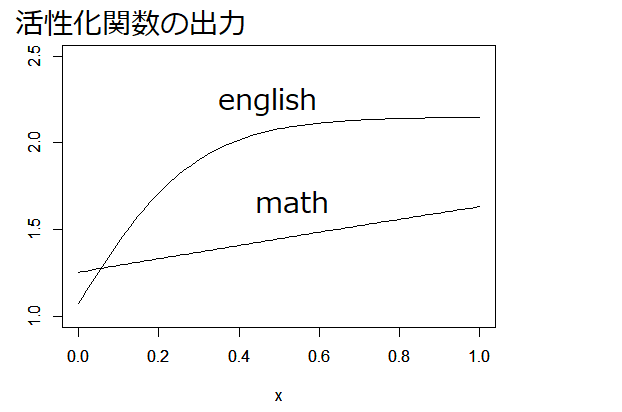
- 英語と数学のシグモイド関数の出力
-
- 数学は80点ぐらいまでは影響なしで、80点から急激に上昇
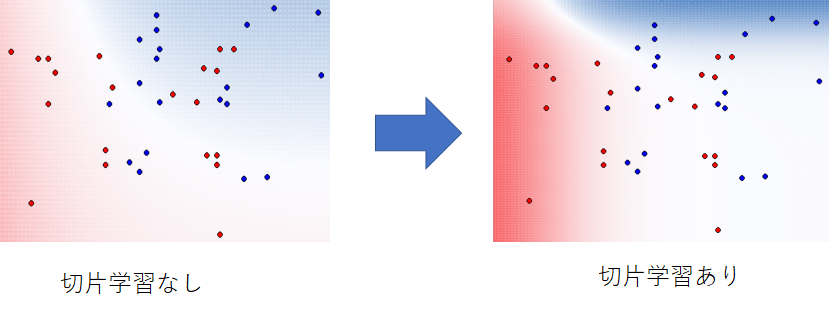
- 二乗誤差7.86 -> 7.16
二乗誤差は減ったが過学習してしまった感
-
確かにデータの感じはよくとらえているが今回の目的（大学の合格可能性を基に示唆を与えるような目的）にはそぐわないか
- 一番下の不合格のサンプルを無視すれば、確かに数学の点が上がっても合格率はそんなに変わらないので、このデータからはこうなるとは思う
- 一方で、事前知識として数学が20点までで合格はしないということが分かっていれば、bを学習しないほうがより、実態に即している。
結論
- bを学習することで二乗誤差が減り、よりデータにフィットした判別が可能
- 問題(データや目的）によってbは学習すべきときとそうでないときがある
Appendix（結果の解釈について）
- 三層と比べて結果を解釈しやすいことが利点だが、どうやって解釈するか。それぞれの特徴量ごとに活性化関数が設定されるので解釈しやすいとはいえ、いくつか注意が必要
- この結果をどう読み解くか
- １．絶対値の大きさは重要ではない。変化量が重要
- 例えば数学は1.3ぐらいから始まっているがそれは数学が0点でも加算されている値であり、判別に影響を及ぼしていない
- ２．シグモイド関数は意外と複雑でグラフを書いてみないと実際よくわからない
- 例えば、重みが負であったとしても負の影響があるとは限らない。ゲインも負ならば正の影響となる
- ３．導関数を書いてみるとよくわかりそうな気がするけど、あんまりよくわからないので、普通に初期値を合わせて書くのが一番わかりやすい
- １．絶対値の大きさは重要ではない。変化量が重要