非線形2層パーセプトロン -DeepLearningはまだ人類には早い-

この記事の目的

• 非線形2層パーセプトロンを作ってみたら意外とよかったので伝えたい
• データサイエンティスト文脈において説明力が必要な局面で使えるのでは
• DeepLearningは全く関係ない
• アドベントカレンダーの穴埋め
• 次回

モチベーション

• データサイエンスでは説明力・ホワイトボックス性・わかりやすさ的なことが重視される場合がある
  • 例1)　認識・予測性能よりも人に知見を与えたい場合
    • 模試の点から大学合格可能性を予測
    • 営業さんに売れそうな訪問先を予測
      • 営業に理由を説明してそこを攻められるようにしたほうが売れる
  • 例2)　なぜそのような判定がされたのか（されるのか）人が見てもわかるほうがいい場合
    • 名刺の名寄せ等、お客さんから理由をよく問われるもの
    • 医療のように失敗が許されにくいもの
  • 例3)　導入初期などで学習データが少ない、あるいはぴったりはまらないものを使っていて、あまり最適化しすぎても仕方がない場合
• このような場合に、わかりやすさ・無駄に最適化しすぎていない点から、特徴量の値に対して結果が単調増加・単調減少になるような判別・予測手法を作りたかった
• さらに、ちょっとライバルに差をつけるために単調増加・減少ではあるが非線形にしたい

提案手法（非線形2層パーセプトロン）の説明

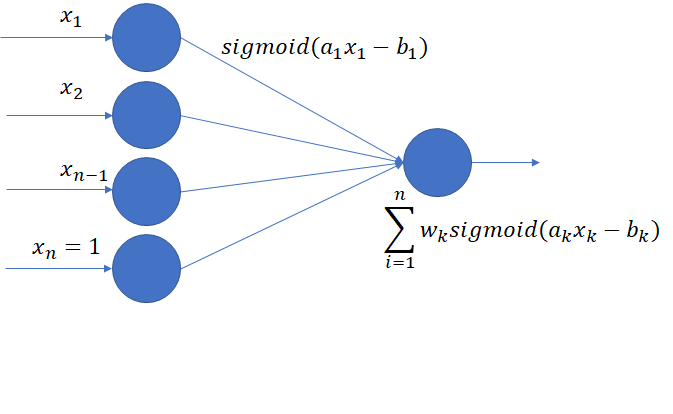
• 図のような2層のパーセプトロンを考える。なお、1層目のニューロンはそれぞれ、活性化関数（シグモイド関数）のゲインa1,a2...,an、初期値b1,b2...,bnを独自に持っていて学習される。一般にゲインの学習はパーセプトロンでは行われないが、これを学習しないともともとの特徴量にシグモイド関数をかけたものの重み付き和でしかなく、線形判別と本質的に違いがなくなる。学習の仕方は特に特別なものはなく、二乗誤差をa,bで偏微分して最急降下方を用いる。

• 

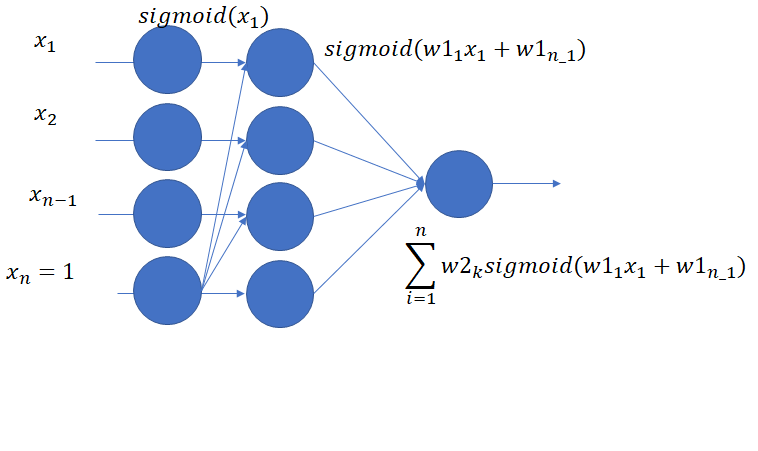
• なお、このモデルは下記のように一般的な3層パーセプトロンに制約を設けたものと等価であり、ニューラルネットワークライブラリを使いこなしている人ならば独自で作るよりも下記のような制約を付けた3層パーセプトロンをライブラリ上で実現するのが良いかもしれない。

• 

実験

実験データ

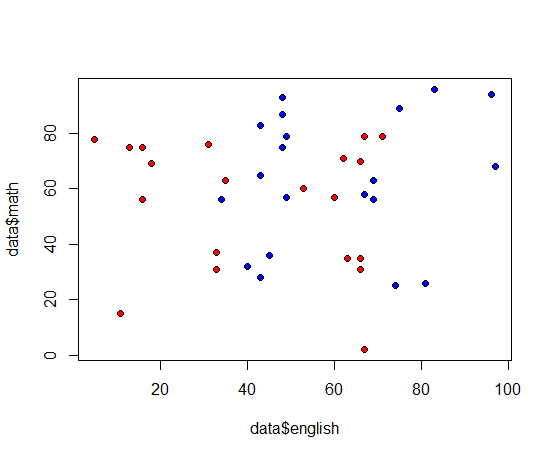
• 模試の結果から大学合格可能性を予測する例として次のようなデータを作成

  • 不合格:英語、数学ともに0~80点までの一様乱数
  • 合格：英語、数学ともに20～100点までの一様乱数を作り、ちょっと非線形要素として英語だけは40点以下だったら＋10する（すなわち合格者だけは、英語は40点台が高密度）
  • 合格、不合格20データずつの40データとする

• 
  赤が不合格（赤点）、青が合格

他の手法との比較

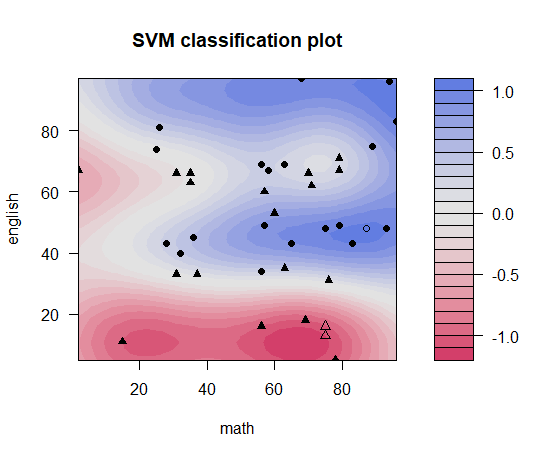
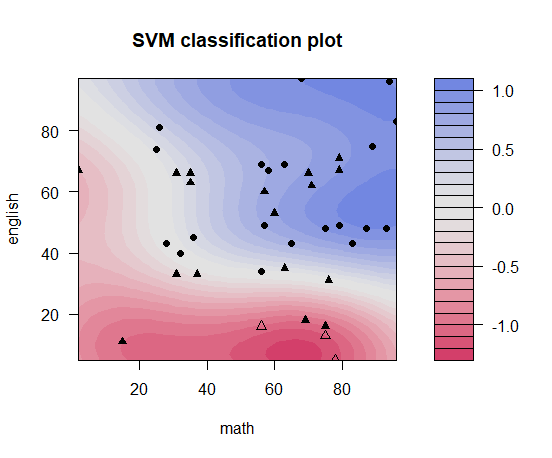
SVM RBFカーネルsigma=0.8

• 

  • たまたま不合格者が多発しているところが不合格ゾーンになってしまう。SVMはモデルがサポートベクトルから作られているため、説明力という意味では、サポートベクトルになったXXさんのデータが君に近かったというような説明しかできないのも欠点。

SVM RBFカーネルsigma=0.5

• 

  • だいぶ良くなった。しかし、このSVMの出力値は2値判別にはいいが、実数地の出力＝合格可能性というふうには使いにくい。得点が上がったのに合格可能性が下がるエリアがあるからである（SVMはそういう使い方をするんじゃないみたいな話もあるが非線形判別（2次判別分析など）は基本的に同様の課題がある)

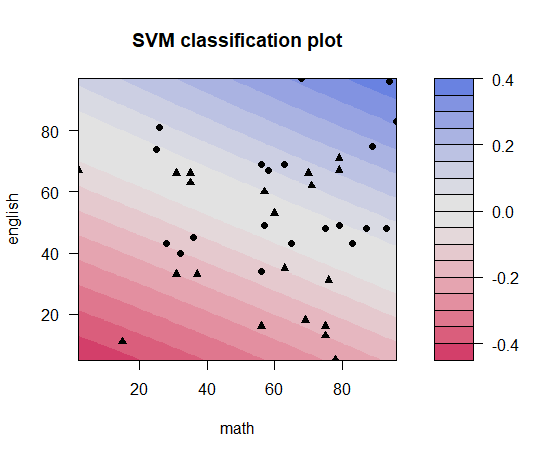
SVM 線形カーネル

• 
• 線形なので単調増加だが数学0点でも合格できるというような判定がされてしまう

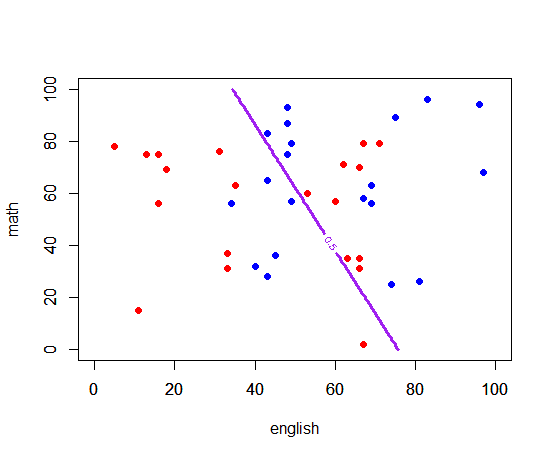
ロジスティック回帰

- 学習結果
    - 英語の係数 0.008214 
    - 数学の係数 0.003397

• 

  • 係数が明に出るので、英語のほうが数学より2倍以上重要そうなことが分かり、説明力が高い。一方、線形なので英語が80点を超えれば数学は0点でもよくなってしまうのは同じ課題である

提案手法

• 2層パーセプトロン学習500000回（今回bは学習せず）

  • 学習結果：
    • 英語のweight = 2.15
    • 数学のweight = 2.51
    • 英語の活性化関数のゲイン=6.8
    • 数学の活性化関数のゲイン=0.62

• 

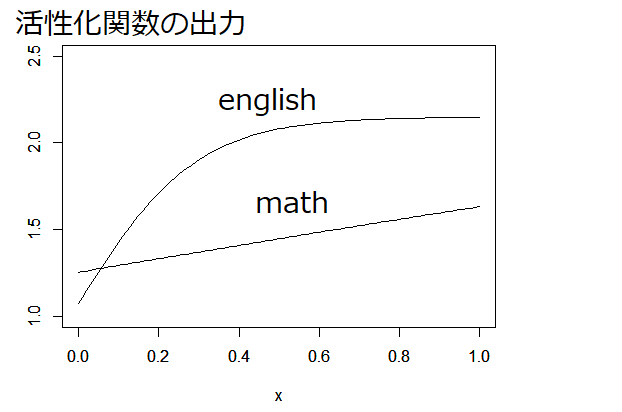
  • ロジスティック回帰の係数にあたる部分が関数になっているので数字だけ見てもどちらがどの程度効果を与えているかがわからないのでグラフを書いてみる。グラフから、ロジスティック回帰と同様、英語のほうが結果に与える影響が高いことが分かる。また英語が急に来るのに対して数学はじわじわ来るというのが分かる。

• 

まとめ

• 非線形2層パーセプトロンでデータに対して単調増加・減少でそこそこわかりやすく、説明力もあるモデルを作ることができた。非線形のため遁減効果を表現することができる。
• 今回はbのほうは動かさなかったがそれも次回やってみたい。また、このモデルでは変数同士の相乗効果的なもの（相関係数）は全く考慮されていないので、そのあたりも次回やりたい