はじめに
前回の記事「将棋の囲いをネットワーク分析で定量化してみた」では,将棋の囲いの駒とひもをノードとエッジに見立てることでネットワークを作成し,ネットワークの特徴量をもとに「囲いの特徴」を定量化してみました.後日この内容について,「囲いの駒の一部を削除してもネットワークの特徴はどれくらい保たれるか」という囲いネットワークの頑健性を調べてみてはどうかという興味深いご意見を頂きました.そこで今回も12種の囲い(矢倉,舟囲い,左美濃,エルモ囲い,雁木,居飛車穴熊,BIG4,美濃,高美濃,銀冠,振り飛車穴熊,中住まい)ネットワークを対象として,この頑健性を調べてみました.
なお,この記事は,@igenki,@splashBob,@karingoの3人で共同執筆しております.
頑健性の定義
囲いのネットワークの頑健性について調べていきます.頑健性とは,「ネットワークからあるノードを削除したときに,ネットワークの強さを表す指標がどの程度変化するか」で表されます.将棋では相手に攻め込まれて駒を取られた際や,他に手がないときにやむを得ず自分から囲いの駒を動かす際など,一局の中で囲いの形が崩れるタイミングがほぼ必ず訪れますが,その時にどの程度強さを維持することができるのかを頑健性を基に調べます.ここでは頑健性を評価するために4つのネットワーク指標に注目し,対象となる囲いの駒(ノード)を一つ削除した場合に,4つの指標が元の状態と比較してどの程度の割合で変化したかを調べました.頑健性評価の4つの指標について,前回も用いた以下の「片美濃ネットワーク」を例に簡単に説明します.
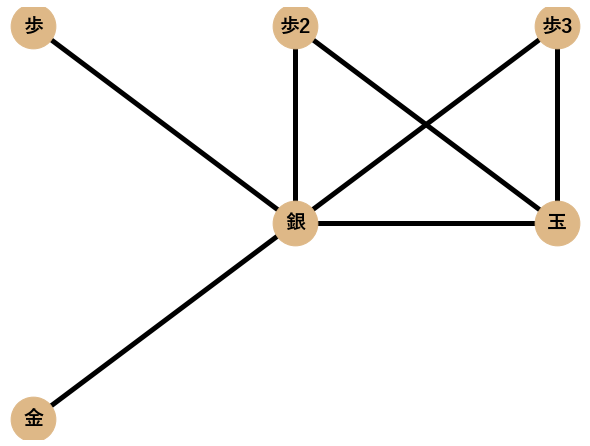
1. 直径
直径とはネットワーク中の全てのノードペアに対する距離の中で最大のもののことです.距離とは,ノードのペア(ノード2つで1ペア)間の最短経路の長さのことであり,例えば,玉から金へは最短で2つの辺で繋がり,銀から歩2へは最短で1つの辺で繋がるので,それらの距離$d$は以下のように表されます.
$$d(玉,金) = 2,d(銀,歩2) = 1$$
例に挙げた片美濃ネットワークでは各駒間の距離$d$は以下のように計算されます.
$d(玉,金) = 2,d(玉,銀) = 1,d(玉,歩) = 2,d(玉,歩2) = 1,d(玉,歩3) = 1,d(金,銀) = 1,d(金,歩) = 2,d(金,歩2) = 2,d(金,歩3) = 2,d(銀,歩) = 1,d(銀,歩2) = 1,d(銀,歩3) = 1,d(歩,歩2) = 2,d(歩,歩3) = 2,d(歩2,歩3) = 2$
よってこの片美濃ネットワークの場合,距離の最大値,つまり直径は2となります.
2. 最大クラスタサイズ
ノードを削除すると,ネットワークが分断されていくつかの小さいネットワークができることがありますが,それらの分かれた部分ネットワークの中で最大のもののサイズが最大クラスタサイズとなります.ノードを削除してもネットワークが分断されない場合は,ネットワークのノードの総数が最大クラスタサイズとなります.元々の片美濃ネットワークの場合は最大クラスタサイズは6であり,そこから以下の図のように銀を削除すると3つの部分ネットワークに分断されます.この中で最大のものは,「玉,歩2,歩3」の部分ネットワークであり,そのサイズである3がここでの最大クラスタサイズとなります.

以下の2つは前回の記事で用いたのと同じ指標になります.
3. 密度
ネットワーク中の全てのノードペアに対する,エッジ数の割合です.無向ネットワークの密度$density$は以下の式で計算されます.
$$ density = \frac{2m}{n(n-1)} $$
ここで$n$はノード数,$m$はエッジ数を表します.片美濃ネットワークでは以下の様に計算されます.
$$density=\frac{2\cdot7}{6(6-1)}=\frac{14}{30}\approx0.47$$
4. 平均次数
次数$k$とは,ノードに結合しているエッジの本数であり,ネットワーク中の全てのノードについて次数の平均が平均次数です.片美濃ネットワークでは以下のように計算されます.例えば,玉は他の3つのノードとつながっているので$k_{玉}=3$となります.
$$k_{玉}=3,k_{金}=1,k_{銀}=5,k_{歩}=1,k_{歩2}=2,k_{歩3}=2$$
よって,平均次数$\langle k \rangle$は,
$$\langle k \rangle=\frac{14}{6}\approx2.33$$
となります.
削除する駒の設定
ネットワークのノードを削除して頑健性を調べるわけですが,各囲いのどの駒を削除すれば良いでしょうか? "次数が一番大きいノードを削除する" ,"ランダムに選んだノードを削除する" といった方法が過去のネットワークの研究では取り扱われています.ただ,将棋の囲いを対象にした場合,次数が一番大きいノードは囲いの中心の駒になりやすいので,一番最初に削除するのは少し変な気がします.
この記事では,"筆者達が考えた,囲いの中で一番取られそうな守り駒" を削除するノードとしました.以下の図で,12種の囲いのそれぞれに対する我々基準の「一番取られやすそうな駒」を赤枠で囲っています1.
1 矢倉

結果:囲いの頑健性の比較
各囲いで上の図の赤枠で囲った1番狙われやすそうな駒が消えた場合に,4つの指標それぞれがどの程度変化するか (=頑健性) を比較します.

直径に関しては変化する囲いとしない囲いの大きく2つに分かれる結果となりました.変化する囲いを見ると美濃囲い系の囲いが多いことが特徴として挙げられるでしょうか.

最大クラスタサイズは高美濃,雁木,美濃の減少率が突出しており,それ以外の囲いはどれも同じくらいの減少率という結果になりました.これらの囲いでは,今回削除した駒が囲い全体の連結の要となっていそうです.


密度と平均次数に関しては,今回選んだ駒が消えることで,多くの囲いでは減少していますが,一部の囲いでは増加しており,両者の変化率の傾向は概ね似ています.密度と平均次数に関しては,駒が消えたことによるエッジの減少数が小さい場合に増加するため,これらがともに増加しているelmo,左美濃は特に,今回選んだ駒が取られた場合でもエッジ(ひも)の数を維持できて被害が少ない囲いと言えそうです.変化率の傾向が似ていることから,将棋の囲いにおいてこれら2つの指標が意味するものは似ていると考えられますが,違いとしては,元々の囲いの密度が高い囲い(BIG4,振り飛車穴熊)は密度の方が増加しやすく,低い囲い(中住まい)は平均次数のほうが増加しやすいという性質があるようです.
まとめ
本記事では,12種の囲いに対して 「一番取られそうな守り駒」 を定義し,「その駒を削除してもネットワークはどの程度保たれるか」という 囲いの頑健性 を分析しました.その結果,バランス重視の囲いは頑健性が低く,固さ重視の囲いは頑健性が高いという傾向がみられました.また,雁木囲い は突出して頑健性が低く,elmo囲い は突出して高いということがわかりました.
NetworkXを用いて特徴量を出力
最後に,頑健性を出力する際に用いたNetworkXのコードを載せておきます.
ネットワークの出力
import networkx as nx
import matplotlib.pyplot as plt
# 9 8 7 6 5 4 3 2 1
# +---------------------------+
# | ・ ・ ・ ・ ・ ・ ・ ・ ・|一
# | ・ ・ ・ ・ ・ ・ ・ ・ ・|二
# | ・ ・ ・ ・ ・ ・ ・ ・ ・|三
# | ・ ・ ・ ・ ・ ・ ・ ・ ・|四
# | ・ ・ ・ ・ ・ ・ ・ ・ ・|五
# | ・ ・ ・ ・ ・ ・ ・ ・ 歩|六
# | ・ ・ ・ ・ 歩 歩 歩 歩 ・|七
# | ・ ・ ・ ・ 金 ・ 銀 玉 ・|八
# | ・ ・ ・ ・ ・ 金 ・ 桂 香|九
# +---------------------------+
# 上の美濃囲いの例を参考に,ノード(駒の種類),エッジ(駒の利き),ポジション(駒の位置)を求める.
nodes = ['歩', '歩2', '歩3', '歩4', '歩5', '金', '銀', '玉', '金2', '桂', '香']
edges = [('香', '歩'), ('金', '歩2'), ('金', '歩3'), ('銀', '歩3'), ('銀', '歩4'), ('玉', '歩4'),
('桂', '歩4'), ('銀', '歩5'), ('玉', '歩5'), ('金2', '金'), ('玉', '銀'), ('金2', '銀'),
('銀', '金2'), ('銀', '桂'), ('玉', '桂'), ('玉', '香')]
pos = {'歩': (9, 4), '歩2': (5, 3), '歩3': (6, 3), '歩4': (7, 3), '歩5': (8, 3), '金': (5, 2),
'銀': (7, 2), '玉': (8, 2), '金2': (6, 1), '桂': (8, 1), '香': (9, 1)}
G1 = nx.Graph() # ネットワークの作成
G1.add_nodes_from(nodes) # ネットワークにノードを追加
G1.add_edges_from(edges) # ネットワークにエッジを追加
# ネットワークの描画
plt.figure(figsize=(8,6))
nx.draw(G1, pos, with_labels=True, node_color = "burlywood", node_size = 2000,
width=5, font_size=20, font_weight="bold", font_family="Yu Gothic")
plt.subplots_adjust(left=0.4, right=0.6, bottom=0.4, top=0.6)
plt.show()
頑健性の出力
- ノードの削除
import copy
G2 = copy.deepcopy(G1) # ネットワークのコピー
target_piece = '金' # 狙われやすい駒の設定
G2.remove_node(target_piece) # ノードの削除
- 直径の変化率
if nx.is_connected(G1) and nx.is_connected(G2): # ネットワークに孤立ノードがあると出力できない
G1_diam = nx.diameter(G1)
G2_diam = nx.diameter(G2)
print('直径の変化率:{}[%]'.format((G2_diam-G1_diam)/G1_diam*100))
- 最大クラスタサイズの変化率
def get_SMC(G):
largest_cc = max(nx.connected_components(G), key=len)
max_cluster = G.subgraph(largest_cc).copy() # 最大クラスタのグラフ
return len(max_cluster) # 最大クラスタのノード数を取得
G1_SMC = get_SMC(G1)
G2_SMC = get_SMC(G2)
print('最大クラスタサイズの変化率:{}[%]'.format((G2_SMC-G1_SMC)/G1_SMC*100))
- 密度の変化率
def get_density(edges,nodes):
return 2*edges/(nodes*(nodes-1))
G1_dens = get_density(G1.number_of_edges(),G1.number_of_nodes())
G2_dens = get_density(G2.number_of_edges(),G2.number_of_nodes())
print('密度の変化率:{}[%]'.format((G2_dens-G1_dens)/G1_dens*100))
- 平均次数の変化率
G1_average_degree = np.average([nx.degree(G1)[node] for node in G1.nodes])
G2_average_degree = np.average([nx.degree(G2)[node] for node in G2.nodes])
print('平均次数の変化率:{}[%]'.format((G2_average_degree-G1_average_degree)/G1_average_degree*100))
ネットワークの描画から特徴量の出力までのコードを,GitHubに載せておきます.
参考文献
-
かなり主観的なのでこの定義は検討の余地がありそうです. ↩










