はじめに

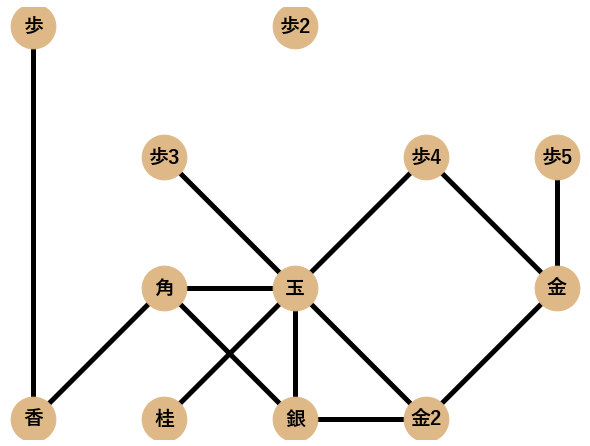
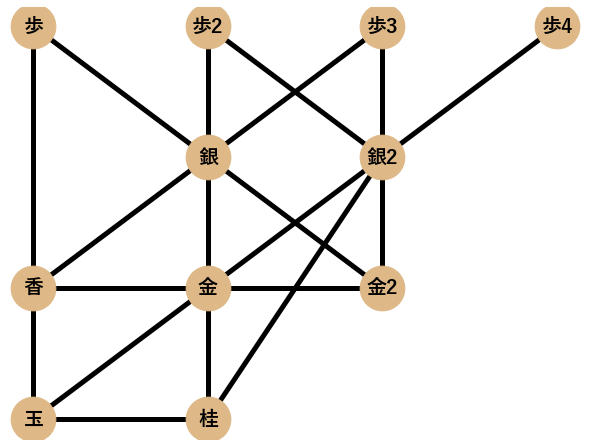
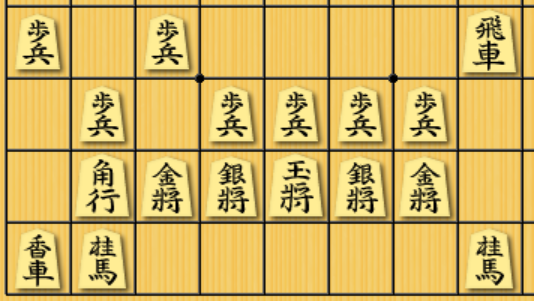
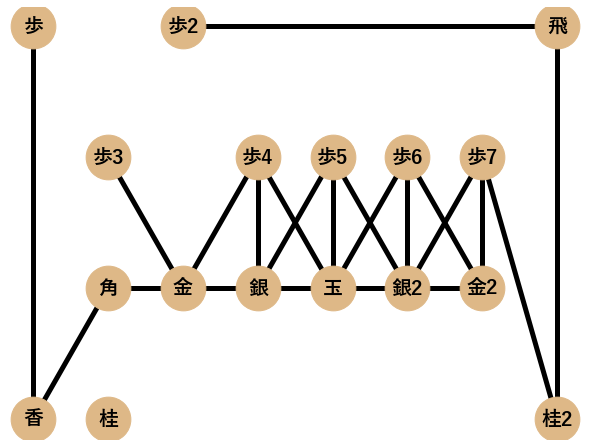
将棋には，囲いと呼ばれる玉を守るための陣形があります．ネットワーク分析を研究している@igenkiには将棋の囲いが以下の右図のようにネットワークに見えてしまいます．

将棋が好きで，ネットワーク分析を研究している私に，ある日，「将棋の囲いをネットワークで表して，ネットワーク分析の指標を使って定量化してみると何か面白いことが分かるのではないか」というアイデアが閃きました（他の人には面白いか分かりませんが…）．そこで，同じく将棋が好きな私の研究室の@splashBobと@karingoと一緒に，これを実際にやってみることにしました．この記事は，@igenki，@splashBob，@karingoの3人で共同執筆しており，以下のネットワークのプログラムは@splashBobと@karingoが作成してくれたものです．

「駒とひも」は「頂点（ノード）と辺（エッジ）」

上でイメージした囲いのネットワークは，将棋用語の「ひも」という考え方に基づいて作られています．将棋では，ある自分の駒Aに他の自分の駒Bが利いている（Bの動けるマスの中にAがいる）状態のことを「（Aに）ひもがついている」と表現します．ひもがついていることによって，Aが相手の駒Cに取られたとしても，BでCを取り返すことができ，駒損を防ぐことができるというメリットがあります．

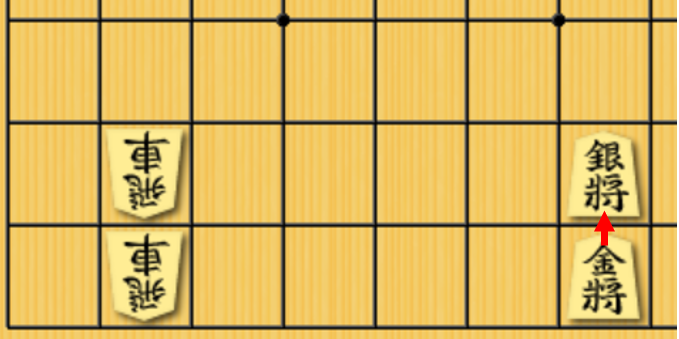
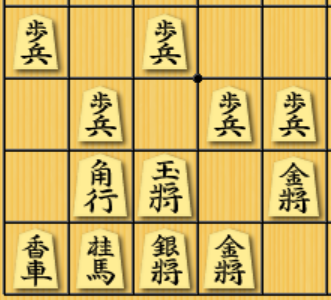
例えば，上のように相手の飛車2枚で自分の金銀が狙われている盤面を考えます．赤い矢印がひもがついていることを示しています．金の方にはひもがついてないので，このまま放置すると飛車で金をただで取られてしまい，大損になります．一方，銀の方には金によりひもがついているため，飛車で銀を取られたとしても，金でその飛車を取り返すことができ，飛車銀交換で駒得することができます．

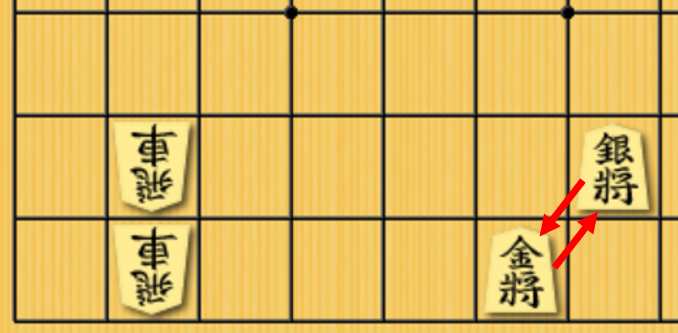
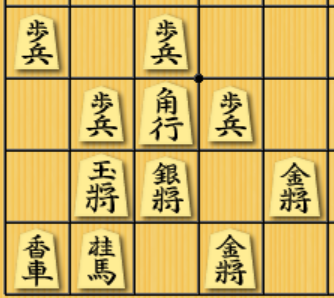
そこから，金を左に動かして上のような形にすると，金と銀どちらにもひもがつき，一方が飛車に取られても，もう一方でその飛車を取り返すことができるようになります．この金銀の配置は，美濃囲いの一部と同じ形であり，駒が相互に連結している非常に良い形とされています．
このように，一般的に将棋では，ひもがついている自分の駒が多いほど，隙がなく良い形であるとされています．今回はこのひもに着目し，囲いを構成する駒を頂点（ノード），駒から駒へのひもを辺（エッジ）としたネットワークを構築し，その特徴を調べることで，囲いの強さの定量化を試みました．

検証

12個の囲いとネットワークによる囲いの可視化

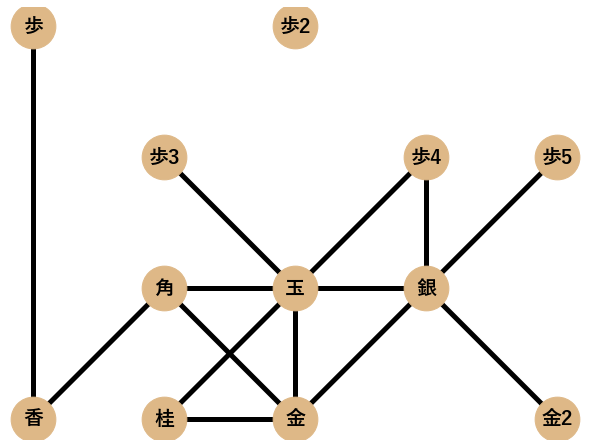
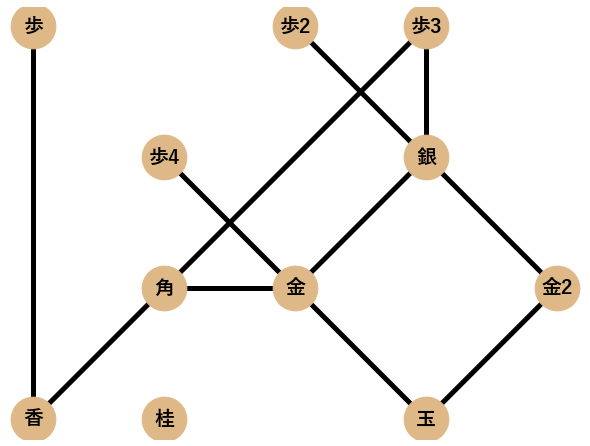
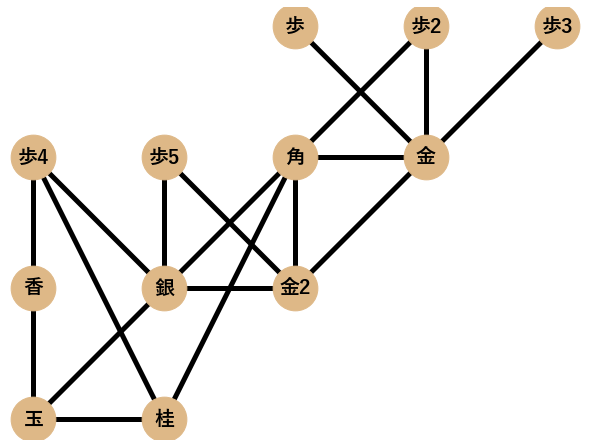
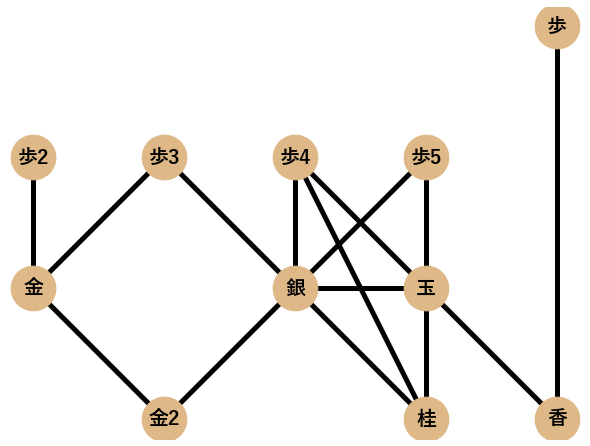
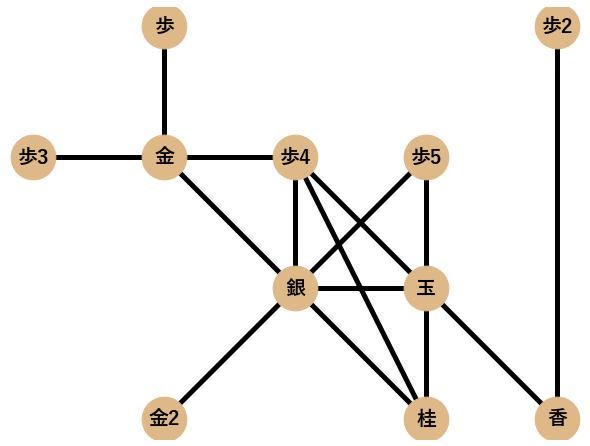
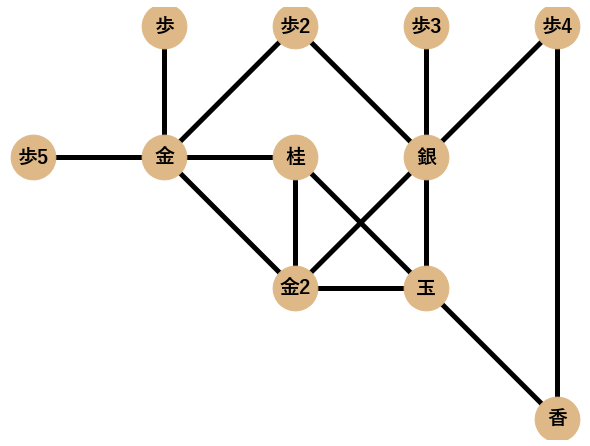
まず，ネットワーク分析によって検証を行う囲い12個（矢倉，舟囲い，左美濃，エルモ囲い，雁木，居飛車穴熊，BIG4，美濃，高美濃，銀冠，振り飛車穴熊，中住まい）を挙げます．各囲いに対してPythonのネットワーク分析ツールであるNetworkXでネットワークとして可視化したものも一緒に載せます．

将棋の囲いは本来，最初に示した美濃囲いのネットワーク図のように，向きと本数（重み）がある重み付きの有向グラフなのですが，今回，ネットワークの特徴量を統一して計算するために無向単純グラフとして可視化・分析することにします¹．

居飛車

居飛車の囲いとして代表的な矢倉，舟囲い，左美濃，エルモ囲い，雁木，居飛車穴熊，BIG4の7個を挙げます．

矢倉
舟囲い
左美濃
エルモ囲い
雁木
居飛車穴熊
BIG 4

振り飛車

振り飛車の囲いとして代表的な美濃，高美濃，銀冠，振り飛車穴熊の４つを挙げます．

美濃
高美濃
銀冠
振り飛車穴熊

その他

中住まい

ネットワークの特徴量

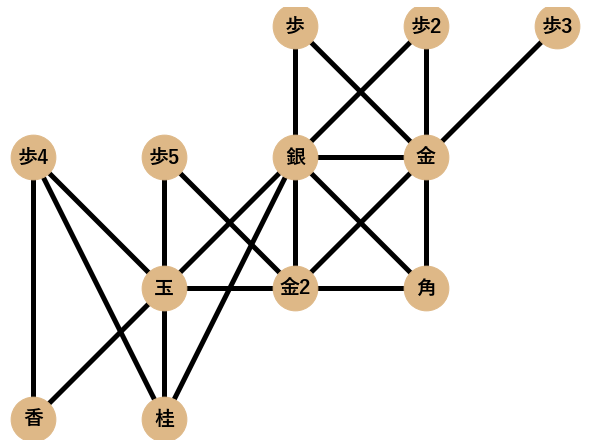
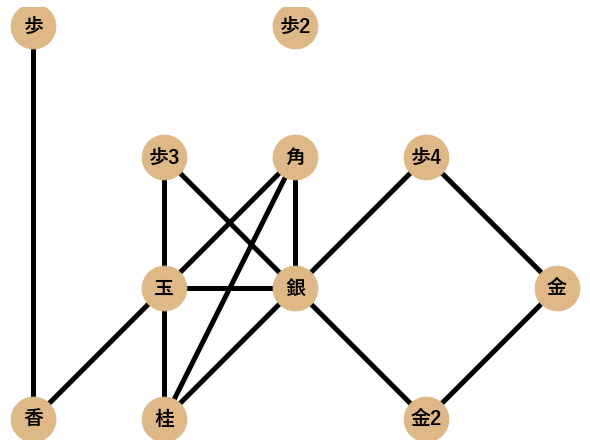
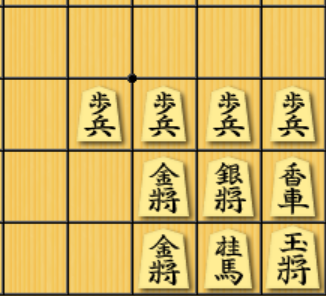
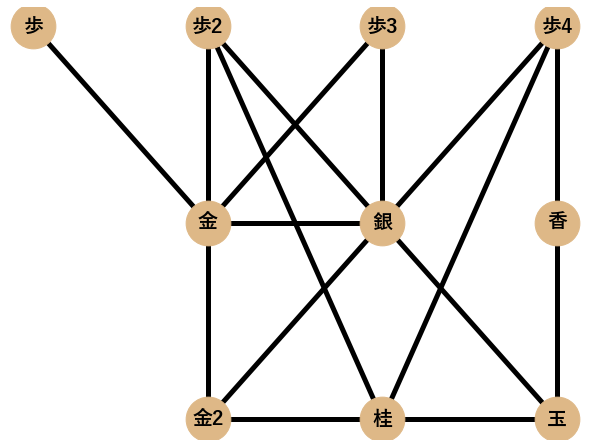
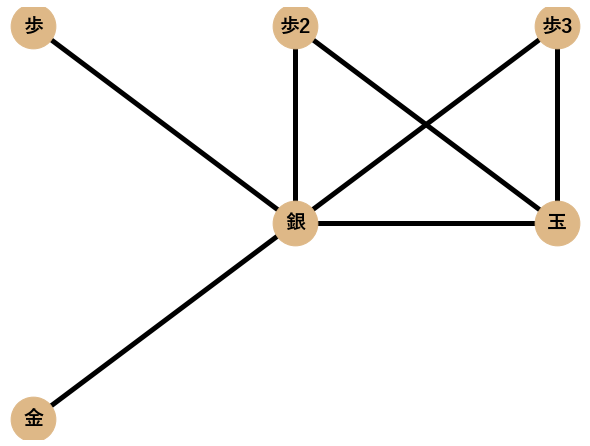
作った囲いのネットワークの特徴量を求めて，それぞれの囲いを比較していきたいと思います．今回は5つの特徴量（平均距離，平均次数，平均クラスタ係数，密度，次数相関）に着目しました．それぞれの特徴量について，以下の片美濃囲いの一部を模したネットワーク「片美濃ネットワーク」を例に挙げて説明します．

平均距離

距離$d$とは，ノードのペア（ノード2つで1ペア）間の最短経路の長さのことであり，例えば，玉から金へは最短で2つの辺で繋がり，銀から歩2へは最短で1つの辺で繋がるので，それらの距離は以下のように表されます．
$$d(玉,金) = 2，d(銀,歩2) = 1$$
平均距離$L$は，ネットワーク中の全てのノードペアについて，距離を求めて平均をとった値であり，例に挙げた片美濃ネットワークでは以下のように計算されます．
$d(玉,金) = 2，d(玉,銀) = 1，d(玉,歩) = 2，d(玉,歩2) = 1，d(玉,歩3) = 1, d(金,銀) = 1，d(金,歩) = 2，d(金,歩2) = 2，d(金,歩3) = 2, d(銀,歩) = 1，d(銀,歩2) = 1，d(銀,歩3) = 1, d(歩,歩2) = 2，d(歩,歩3) = 2, d(歩2,歩3) = 2$
$$L=\frac{23}{15}\approx1.53$$
ただし，今回取り上げる12個の囲いでは他の駒とつながっていない孤立ノードが存在する場合があります（例えば，舟囲いの歩2など）．その場合は，孤立ノードを除いて最短距離の平均値を計算するものとします．

平均次数

次数$k$とは，ノードに結合しているエッジの本数であり，ネットワーク中の全てのノードについて次数の平均が平均次数です．片美濃ネットワークでは以下のように計算されます．例えば，玉は他の3つのノードとつながっているので$k_{玉}=3$となります．
$$k_{玉}=3，k_{金}=1，k_{銀}=5，k_{歩}=1，k_{歩2}=2，k_{歩3}=2$$
よって，平均次数$\langle k \rangle$は，
$$\langle k \rangle=\frac{14}{6}\approx2.33$$
となります．

平均クラスタ係数

クラスタ係数とは，あるノードに着目した時，そのノードとエッジで結ばれているノード同士がエッジで結ばれている割合です．ネットワーク中の全てのノードのクラスタ係数について，平均をとった値が平均クラスタ係数になります．平均クラスタ係数はネットワーク中に三角形がどれくらいあるかということを数値化しています．ノード$i$のクラスタ係数$C_i$は，次数$k_i$を用いて以下のように求めることができます．
$$ C_i=\frac{ノードiを含む三角形の数}{k_i(k_i-1)/2} $$
例えば，ノード[玉]のクラスタ係数は下図を参考にすると，$C_玉=\frac{2}{3 \cdot 2/2}=\frac{2}{3}$となります．

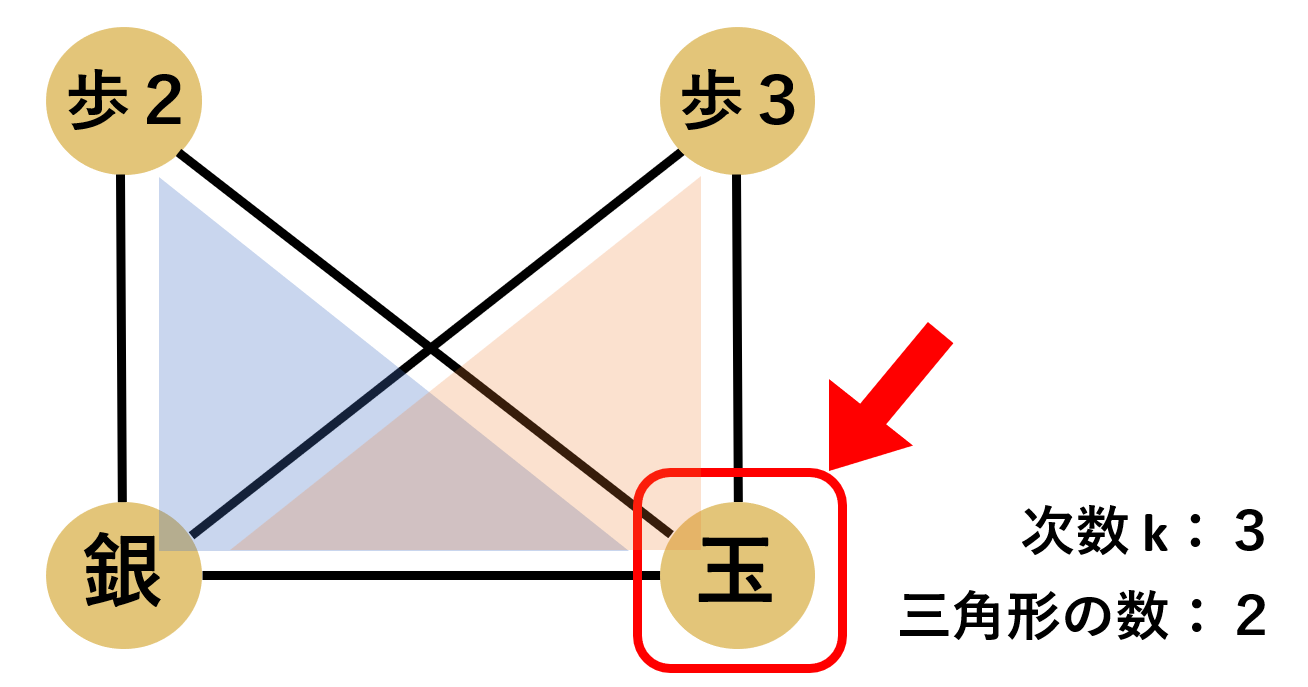
よって，片美濃ネットワークの平均クラスタ係数$C$は以下のようになります．
$C_玉=\frac{2}{3}，C_金=0，C_銀=\frac{1}{5}，C_歩=0，C_{歩2}=1，C_{歩3}=1$
$$ C=\frac{2/3+1/5+1+1}{6}\approx0.478 $$

密度

ネットワーク中の全てのノードペアに対する，エッジ数の割合です．今回のような無向ネットワークの密度$density$は以下の式で計算されます．
$$ density = \frac{2m}{n(n-1)} $$
ここで$n$はノード数，$m$はエッジ数を表します．片美濃ネットワークでは以下の様に計算されます．
$$density=\frac{2\cdot7}{6(6-1)}=\frac{14}{30}\approx0.47$$

次数相関

ネットワーク中で隣接する全てのノードペアについて，ノードペアの次数の類似性を数値化した値です．高次数ノードどうし，低次数ノードどうしが隣接しやすい場合は正の値を，高次数ノードと低次数ノードが隣接しやすい場合は負の値をとります．計算式はここでは割愛しますが，片美濃ネットワークの場合，次数相関は$-0.77$となります．

囲いの特徴量の比較

最後に，12個の囲いにおけるネットワークの特徴量がどのようになったかを見てみます．

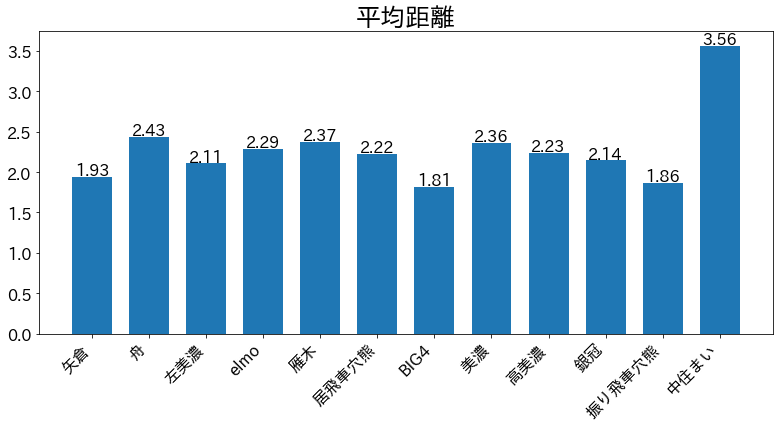
平均距離は，2ノード間を最短で結ぶエッジ本数の平均なので，この値が低いほど駒同士が密集している（=「堅い」）囲いであり，高いほど玉の逃げ道が多い（=「広い」）囲いであると言えそうです．振り飛車穴熊やBIG4，美濃囲いの値が低くなっており，それぞれの囲いのイメージとも一致しています．そのため，囲いの広さや堅さの指標として，平均距離はある程度有効な指標ではないかと思います．それでいくと，唯一違和感を感じるのは矢倉が居飛車穴熊よりも低い値をとっていることでしょうか．

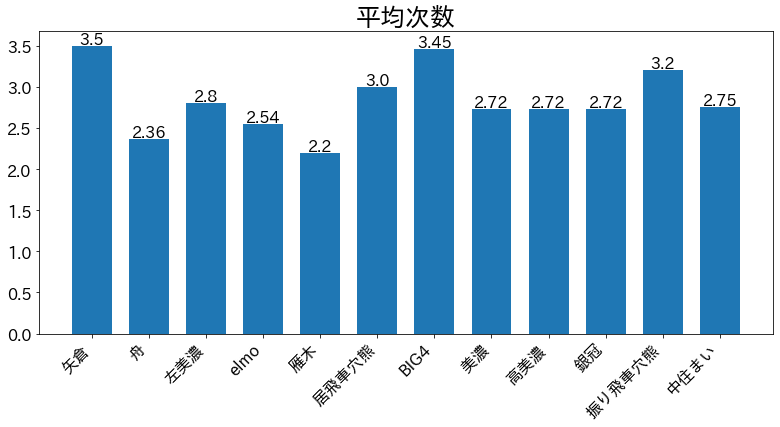
平均次数はノードにつながるエッジの本数の平均なので，この値が高いほどひもがついている駒が多く，連結のよい囲いであると言えそうです．今回の囲いの中だと舟囲いと雁木が低めの値になっています．この2つの囲いには共通して，比較的「薄い」というイメージがあります．囲いが薄いとはどういう状態であるかを考える際には，駒同士の連結が一つの指標になりそうです．また，高い値をとっている囲いを見ると，矢倉，BIG4，振り飛車穴熊が該当します．平均距離でもそうでしたが，矢倉が穴熊系統の囲いと同等以上の値をとっているのは少し意外に思えます．他に気になる点は，美濃，高美濃，銀冠の値が横並びになっていることでしょうか．

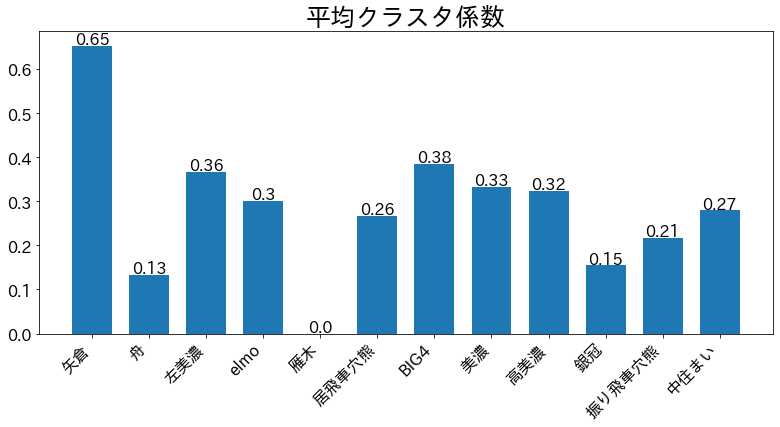
平均クラスタ係数は，任意の3つの駒とエッジからなる三角形が多いほど高い値となります．3つの駒の位置関係によって値が決まるという意味で，コンピュータ将棋の3駒関係に似ているかもしれません．ここでも雁木と舟囲いの値が低く，この値も囲いの薄さと少しは相関があるかもしれません．

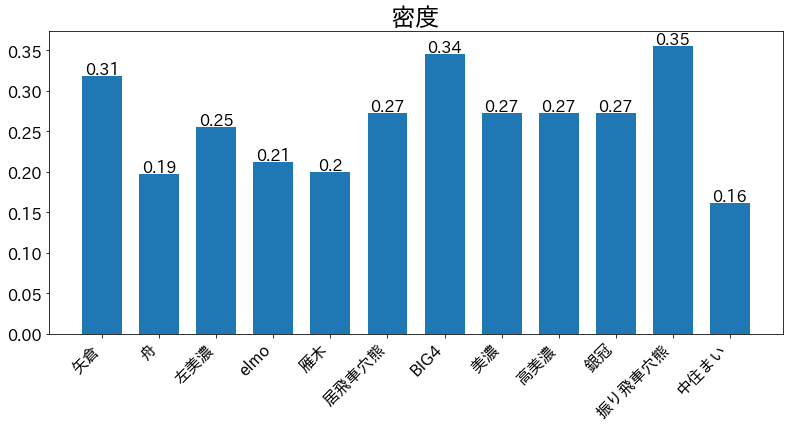
密度はノード数に対するエッジ数の割合なので，この値が高いほど限られた駒数で効率よく連結していると言えそうです．穴熊系統の囲いは密度が大きくなるだろうと予想していましたが，同じ穴熊でも居飛車穴熊と振り飛車穴熊で大きな差が見られます．

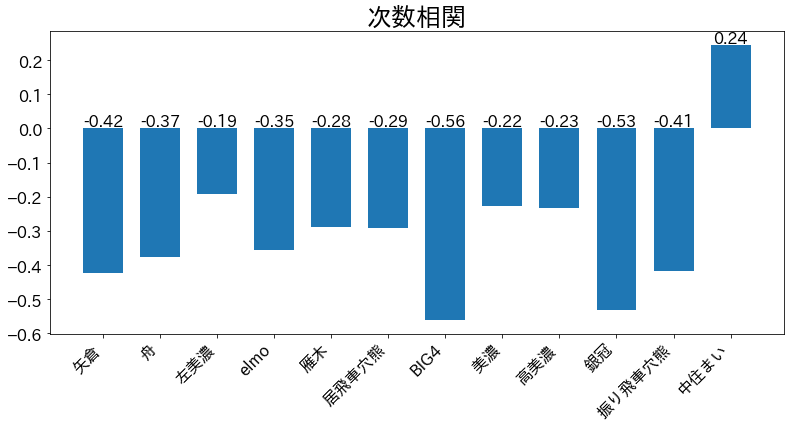
次数相関は連結しているノード同士の次数の類似性を表します．これを将棋の囲いにおいてどのように解釈するかは難しいところですが，基本的に将棋の囲いには強い箇所と弱い箇所が両方存在することから，囲いのネットワークには高次数ノードと低次数ノードがともに含まれると予想されるため，中住まいのように次数相関が高いほど，連結のよい部分と悪い部分が分かれている，弱点の地点がはっきりしている，などのことが言えるでしょうか．

結論：どの特徴量が囲いの特徴をよく表すか？

本記事では，将棋の囲いの 駒とひも を ノードとエッジ に変換してネットワークを作成し，「囲いの特徴」をネットワークの特徴量によって定量化しました．特徴量の中でも，平均距離 と密度が実際の囲いの特徴を表現しているように感じます．BIG4や振り飛車穴熊のような堅い代わりに玉が狭い囲いは，平均距離が小さく，密度が高くなり，その一方で，舟囲いや雁木のように玉が広い代わりに薄い囲いは，平均距離が大きく，密度が低くなるという結果となりました．

おまけ

矢倉は，一般的に最強の囲いとされているBIG4と多くの項目で近い値をとっており，平均クラスタ係数は全囲いの中でダントツになっています．矢倉には私たちのまだ知らない可能性が隠されているのかもしれません．

NetworkXを用いて特徴量を出力

最後に，特徴量を出力する際に用いたNetworkXのコードを載せておきます．

ネットワークの出力

import networkx as nx
import matplotlib.pyplot as plt
#   ９ ８ ７ ６ ５ ４ ３ ２ １
# +---------------------------+
# | ・ ・ ・ ・ ・ ・ ・ ・ ・|一
# | ・ ・ ・ ・ ・ ・ ・ ・ ・|二
# | ・ ・ ・ ・ ・ ・ ・ ・ ・|三
# | ・ ・ ・ ・ ・ ・ ・ ・ ・|四
# | ・ ・ ・ ・ ・ ・ ・ ・ ・|五
# | ・ ・ ・ ・ ・ ・ ・ ・ 歩|六
# | ・ ・ ・ ・ 歩 歩 歩 歩 ・|七
# | ・ ・ ・ ・ 金 ・ 銀 玉 ・|八
# | ・ ・ ・ ・ ・ 金 ・ 桂 香|九
# +---------------------------+
# 上の美濃囲いの例を参考に，ノード（駒の種類），エッジ（駒の利き），ポジション（駒の位置）を求める．
nodes = ['歩', '歩2', '歩3', '歩4', '歩5', '金', '銀', '玉', '金2', '桂', '香']
edges = [('香', '歩'), ('金', '歩2'), ('金', '歩3'), ('銀', '歩3'), ('銀', '歩4'), ('玉', '歩4'), 
        ('桂', '歩4'), ('銀', '歩5'), ('玉', '歩5'), ('金2', '金'), ('玉', '銀'), ('金2', '銀'), 
        ('銀', '金2'), ('銀', '桂'), ('玉', '桂'), ('玉', '香')]
pos = {'歩': (9, 4), '歩2': (5, 3), '歩3': (6, 3), '歩4': (7, 3), '歩5': (8, 3), '金': (5, 2),
       '銀': (7, 2), '玉': (8, 2), '金2': (6, 1), '桂': (8, 1), '香': (9, 1)}
       
G = nx.Graph()  # ネットワークの作成
G.add_nodes_from(nodes)  # ネットワークにノードを追加
G.add_edges_from(edges)  # ネットワークにエッジを追加

# ネットワークの描画
plt.figure(figsize=(8,6))
nx.draw(G, pos, with_labels=True, node_color = "burlywood", node_size = 2000, 
        width=5, font_size=20, font_weight="bold", font_family="Yu Gothic")
plt.subplots_adjust(left=0.4, right=0.6, bottom=0.4, top=0.6)
plt.show()

特徴量の出力

平均距離
ノードを除く操作をしているので，この特徴量は最後に算出するのが望ましい．

# 次数が0のノード（孤立ノード）を除く という操作を最初に行う．
remove_nodes = [nodes for nodes in G if G.degree(nodes) == 0]
G.remove_nodes_from(remove_nodes)

# 平均距離の算出
nx.average_shortest_path_length(G)

平均次数

import numpy as np

# NetworkXのinfo()という組み込み関数で平均次数の情報も出してくれますが，以下では直接計算する．
# nx.degree(G)[node]でネットワークGにおけるあるnodeの次数を取得できるので，
# 各ノードの次数をリストに格納し その平均を得る．
np.average([nx.degree(G)[node] for node in nodes])

平均クラスタ係数

nx.average_clustering(G)

密度
NetworkXのdensity()という組込み関数で計算できますが，以下では直接計算しています．

E = G.number_of_edges()  #エッジ数を取得
N = G.number_of_nodes()  #ノード数を取得  
degree_density = 2*E/(N*(N-1))

次数相関

nx.degree_assortativity_coefficient(G)

ネットワークの描画から特徴量の出力までのコードを，下のリンクにあるGitHubに載せておきます．
https://github.com/IkeHide/KAKOI_network.git

動画解説

以上の内容を研究者ゲンキの以下の動画で解説しています．

主に動機と結果の解説

特徴量の具体的な計算とプログラムコードの解説

参考文献

謝辞（以下のサイトに感謝いたします）

将棋の盤面は将棋GUIソフト「将棋所」を用いて作成しています．
将棋の駒は素材のプチッチのイラストを用いています．

もちろんこの単純化によって重要な特徴が抜けてしまう可能性はあります． ↩

将棋の囲いをネットワーク分析で定量化してみた