はじめに
Pythonを用いたネットワークの分析・可視化では、NetworkX がよく用いられます。しかし、ノード数1万超えのような大規模なグラフを扱う際には時間がかかるというデメリットがあります。
そこで今回は、NetworkXと同様にPython上で実行できる「igraph」1を用いて、どれくらい高速に実行できるかを検証します。
この記事の対象者
- NetworkXを使ったことがある
- 計算社会科学や大規模ネットワークの可視化に興味がある
実験の前に
igraphとは
igraphはC/C++系の言語で作られたオープンソースライブラリで、RやC言語、Pythonのインターフェースを提供しています。ネットワーク可視化ライブラリには、Networkx 以外にも graph-tool や Gephi 等がありますが、igraphはPython上でpip installだけで簡単に、かつ高速に実行できる点が魅力です (APIも不要)。
しかし日本語のドキュメントや記事が少なく、igraphが本当に高速か分からなかったので、本記事を執筆しました。igraphについては、こちらの記事でも説明されています。
- 【python igraph】pythonでigraphを使う (fz5050さん)
- [Python]インスタ映えする決定木を描く (@nekoumei さん)
実験準備
今回の実行ノートブックはGithub上に公開しています。
まず、ノード数が n_nodes 、平均次数が avg_degree のランダムグラフを作成します。
ノード は頂点、 エッジ は辺のこと2で、次数 は、各ノードが持つ辺の数です。例えば、ノードの数を10、平均次数を2とした時は、以下の図のようにエッジは10本になります(直感的には10×2=20本ですが、各エッジは2つのノードから成るので、10×2/2=10本となります)。
実験1では平均次数を固定し、ノード数を変化させます。
実験2ではノード数を固定し、平均次数を変化させます。
これにより、NetworkXとigraphそれぞれでネットワーク描画の実行時間を計測します。
ネットワーク描画の実装
次に、ネットワーク描画を実装します。なるべく同条件となるように、グラフの準備、nodesとedgesの追加、中心性(pos)の定義3、可視化4の手順で実装します。
NetworkXの実装
def draw_networkx(nodes, edges):
# prepare
G_nx = nx.Graph()
G_nx.add_nodes_from(nodes)
G_nx.add_edges_from(edges)
pos = nx.kamada_kawai_layout(G_nx)
# plot
fig, ax = plt.subplots(figsize=(5, 5))
nx.draw(G_nx, pos, node_size=10, width=0.5, with_labels=False, ax=ax)
plt.axis("off")
plt.show()
graphiの実装
def draw_igraph(nodes, edges):
# prepare
G_ig = ig.Graph()
G_ig.add_vertices(nodes)
G_ig.add_edges(edges)
pos = G_ig.layout("kk")
# plot
fig, ax = plt.subplots(figsize=(5, 5))
ig.plot(G_ig, layout=pos, target=ax, vertex_size=5, edge_width=0.5, vertex_label=None)
plt.axis("off")
plt.show()
上記のように、NetworkXとigraphは同様の形式で実装できることが分かります。
実験結果
次に、各実験の結果を説明します。
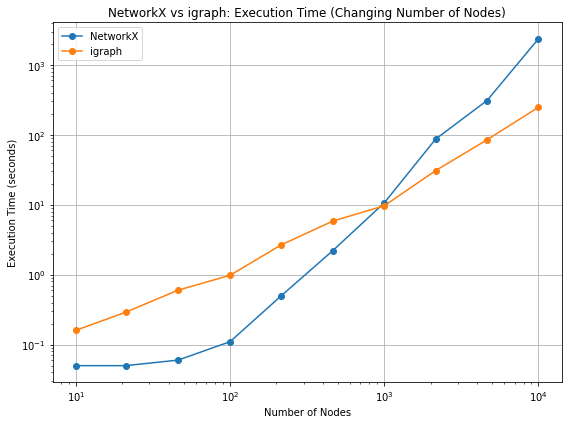
実験1: 平均次数を2に固定し、ノード数を変化させた場合の実行時間の比較
まず平均次数を2に固定し、ノードの数を10から10,000まで、対数で変化させます5。
下記は横軸・縦軸を対数変換した結果の図です。
図より、ノード数が少ない場合はNetworkXのほうが速いですが、1,000($10^3$)で逆転し、それ以降はigraphの方が速いことが分かります。
実験1の結果を以下の表にも示します。
| ノードの数 (number of Nodes) 5 |
エッジの数 (Number of Edges) |
NetworkX Time (s) |
igraph Time (s) |
時間比率 (NetworkX/igraph) |
|---|---|---|---|---|
| 10 | 10 | 0.05 | 0.16 | 0.3 |
| 21 | 21 | 0.05 | 0.29 | 0.17 |
| 46 | 46 | 0.06 | 0.60 | 0.1 |
| 100 | 100 | 0.11 | 0.98 | 0.1 |
| 215 | 215 | 0.50 | 2.67 | 0.2 |
| 464 | 464 | 2.21 | 5.84 | 0.4 |
| 1000 | 1000 | 10.63 | 9.66 | 1.1 |
| 2154 | 2154 | 86.94 | 30.77 | 2.8 |
| 4641 | 4641 | 309.36 | 84.88 | 3.6 |
| 10000 | 10000 | 2364.59 | 247.94 | 9.5 |
「時間比率」は、igraphがNetworkXの何倍高速かを表します。
つまり、ノード数が10,000個の時にはigraphの方が9.5倍高速であることが分かります。時間差としては40分vs4分なのでかなり大きいですね。ノード数が1,000より少ない場合にはNetworkXの方が速いですが、速いといっても3~4秒程度なので、igraphの方が実用性は高そうです。
ちなみに、プロット例は以下のようになりますが、(軽い)集合体の図なので閲覧にはご注意ください。(詳しいプロットはこちら)
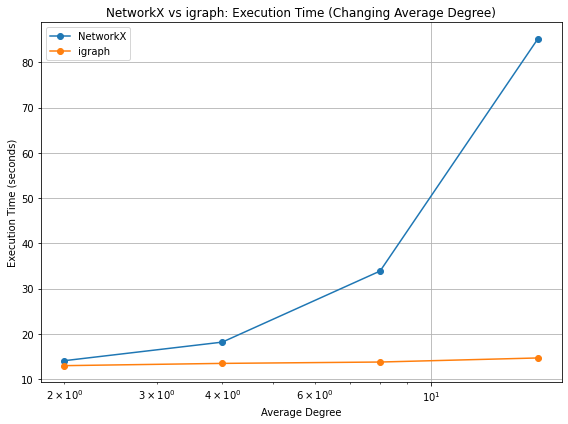
実験2: ノード数を1,000に固定し、平均次数を変化させた場合の実行時間の比較
今度はノード数を1,000に固定し、平均次数を2,4,8,16と変化させてみます。(分かりやすさのため、x軸のみ対数変換)
この場合、平均次数が2(つまりエッジ数が1000*2/2=1000)の時は実行時間はどちらも15秒程度なのに、平均次数が16の時はigraphは14.7秒に対してNetworkXは85.2秒というように、5.8倍高速であることが分かります。
よって、限定的な実験ではありますが、igraphはNetworkXと比べ、平均次数を増やしても処理時間の変化は小さいようです。
まとめ
今回の検証で得られた結論は以下となります。
実験1では、ノード数が1万でも4分程度で実行できたのは嬉しいですね。参考までに、自身の研究で用いるネットワーク (ノード数:1.3万、平均次数:60、エッジ数:81万)のデータでも試しましたが、9分弱で実行できたので実用性も高そうです。
一方で、まだ私自身もigraphを触ってから短く、見落としている点があるかもしれないので、より良い検証方法や不明点ありましたらご連絡いただけると幸いです。6
ここまでお読みいただき、ありがとうございました!
-
ちなみに、igraphは「iGraph」というタグで登録されていますが、公式のドキュメントでは「igraph」と記載されているので本記事はそちらで表記しています。 ↩
-
ネットワークの用語は分野により異なり、ネットワークのことをグラフと読んだり、ノードをバーテックス、エッジをリンクと呼ぶこともあります。(参考書籍:ネットワーク科学入門) ↩
-
igraphのドキュメントのチュートリアルを参考に、中心性にはkamada_kawai(kk)を用いています。 ↩
-
NetworkXでは
plt.subplots()を用いなくてもnx.draw(G)で描画可能ですが、こちらもigraphに合わせています。 ↩ -
np.logspace(1, 4, num=10, dtype=int)により、10~10,000を10個に対数分割 ↩ ↩2 -
今回考慮できてない点として、まずノード数・平均次数の片方を固定しているので、それらを両方変化させた時の実験が含まれていない点があります。また1回の実行結果のみを用いているため、環境等による結果が異なる可能性があります。また、大規模なネットワークへ適用できるか、より次数を高くしたらどうなるか、というigraphの限界まで調査しきれていないため、これらは必要ならば追加で検証しようと思います。 ↩