モチベーション
電子取引が盛んになってから、海外ではアルゴリズム取引が爆発的に人気になりました。
コンピュータによる売買であまりにも流動性が増えたため、フラッシュクラッシュ(株価の急激な変化)が起きた時は、アルゴリズム取引が悪者にされたりしましたよね。
今では市場の出来高の80%~90%はコンピュータによる売買とまで言われています。
そんな時代ですから、マニュアルでトレーディングする方々もアルゴリズム取引を直接やらずとも、アルゴリズム取引がどういうことを行っているのかについて理解することが大事になっていると思います。
この前の記事アルゴリズム取引を始めよう! ~イントロダクション~では学ぶにあたって要求される予備知識及び無料オンライン学習コンテンツを紹介しました。
ここでは、学び始める方や既に学んでいる方々のために、分析するときの注意点について話したいと思います。
金融市場の分析において、往々にしてあるのが、調査結果に何かしら論理的な穴があり、全く意味のない結論を出してしまうことです。
こういったことを完全に避けることは難しいですが、今回はどのような論理的な過ちを犯しやすく、その対処法について紹介したいと思います。
中にはかなり重い内容もあり、キーボード叩き過ぎてキーが弾けました(笑)
アジェンダ
基本的には、こちらの論文(THE 10 REASONS MOST MACHINE LEARNING FUNDS FAIL, Marcos López de Prado [2018])に沿って解説していきますが、せっかくなので、実務家として現在金融業界で働いている身として、一部の解決策に対してコメントもしたいと思います。
流れとしましては、次を想定しております。
- 問題(例え話で問題提起する場合もあります)
- 解決策
- 書評
では、10個の課題を一緒に解決していきましょう!
#1 シーシュポスの模範
※ここでは裁量のポートフォリオを神話に登場する人物で例えています。
裁量のポートフォリオマネジャー達が、特定の理論や理論的根拠に従わないように投資判断をしていたとします(している場合は、システマティックPMですが)。彼らは、ニュースの分析等に時間を費やし、ほとんどの投資の意思決定は、自身の判断や直感に基づいているとします。彼は自身の意思決定をある物語に基づいて合理的に話せますが、全ての決定には常に物語があります。なぜなら、誰も自身の賭けを裏付けするロジックについて完全に理解することは出来ず、投資会社は多様化のためにお互い独立に働くように要求するからです。
それぞれのPMは特定の逸話的な情報に取りつかれており、議論の大きな飛躍は事実ベースや経験的な証拠が無いために作られています。
これは、裁量のポートフォリオマネジャーが成功出来ないとは言っていません。
**要点は、裁量のポートフォリオマネジャーはチームとして働くことが出来ないことです。**50人の裁量のポートフォリオマネジャーがいたら、彼らは貴方が一つの仕事に50人分の給料を支払うまで互いに影響を及ぼし合います。なので、彼らはお互い極力干渉せず、単独で働くことは理にかなっていますということを言いたいのです。
現実的なケースでは、定量的な、またはMLプロジェクト等へ公式を応用するときに、会議室での精神状態は、大体これを裁量ポートフォリオマネジャーと一緒に働いたことのあるクオンツと一緒にやりたいという感じです。50人のPhDを雇用し、彼らに6か月以内に投資戦略を作らせよう等みたいなことです。
こういったアプローチで、PhDの方々は死に物狂いで投資戦略を探そうとしますが、最終的にバックテストがオーバーフィットして、偽陽性(False Positive : 意味 「真の陰性」の検査結果が「間違って陽性」と判定されること)の確率を高めることまたは、少なくとも学術的に支持を得ているような低いシャープレシオと分かっている一般的なファクター投資戦略に行きつく可能性が高い。
どちらの結果も落胆するでしょうし、プロジェクトを中断せざるを得なくなります。
仮に5人の博士が良い発見をしたとしても、利益は50人分の支出を満足に補うのは難しいでしょう。
こういった問題に対する解決策を提案します。
解決策: メタ戦略の模範
もし私たちが機械学習戦略の開発を要求されたら、私たちに期待が積み重なるでしょう。
百個の投資戦略を生み出す努力をして、やっと一つの良い投資戦略が生み出され、そして、とんでもなく複雑になるでしょう(データ整形、高機能計算(HPC: High Performance Computing)インフラ、特徴量分析、執行シミュレーション、バックテスト等)。
例え、ある企業が私たちに似たようなサービスを提供したとしても、BMWの開発向上で一から車を作るワークショップに参加させられているような気分になるでしょう。最初の週で溶接工をマスターし、次の週は電気技師、さらに次の週は機械工学、また別の週はペンキ屋と...
私たちは挑戦し続けては溶接工に戻るというサイクルと繰り返し、はたしてこれに意味があるのでしょうか?
私が見てきた成功している定量分析の会社はメタ戦略の模範を応用しています(López de Prado [2014])。組み立ての流れ作業は、明確に部分的なタスクに分かれています。クオリティは独立に評価され、それぞれのタスクで監視されています。それぞれの役割のクオンツは特定のタスクに専念し、そのタスクに対してベストを尽くす一方で、全体のプロセスを見渡しています。チームワークとしては運任せではなく、予測出来るレベルでの発見を生み出します。誰一人として、その発見に対して責任を持たず、その調査結果はみんなの努力と貢献によります。
もちろん、こういった金融研究所を設立するには時間がかかりますし、経験者も必要です。
しかし、あなたは、このような組織的な協力の模範が成功しやすいのか、それともシーシュポスの模範(全てのクオンツに山を登らせる)が成功しやすいのか、どちらだと思いますか?
書評:これはあらゆるビジネスで大事だと思います。私は実際全ての研究開発工程を自力で行っておりますが、その中で、やはりそれぞれの工程を明確化しております。技術的にこれを行うためには、データベース構築から学んだ方が良いと思います。なぜなら、あらゆる工程の作業を独立にしなければならない一方で、あらゆる工程の作業が最終成果物へ影響するからです。これを技術的に解決できる一番簡単な手段は、データベースを構築して、あらゆる工程で、そのデータベースから情報を参照して研究開発を行うことです。技術の発達のおかげで、今ではdockerというサービスを用いれば、データベースはすぐに立ち上がるので、最初の学習コストはもちろんかかりますが、一回出来ればそこまで大変ではありません。
#2 バックテストによるリサーチ
**問題点:**金融のリサーチにおける最も犯しやすい過ちの一つに、データを取得し、機械学習アルゴリズムを適応し、予測に対してバックテストを行い、この一連の動作をバックテストが良い結果になるまで行うことです。学術的なジャーナルでも、こういった間違えた発見がなされていることが多く、大きいヘッジファンドでさえもこのトラップに陥りやすいです。
これは、アウトオブサンプルにおけるウォークフォワード法によるバックテストでも関係ありません。
問題なのは、同じデータで何度もテストを実行し、誤った発見が見つかる可能性を挙げることなのです。
この方法論的な過ちは、統計学者の間では非常に悪名高く、米統計委員会(American Statistical Association)は倫理的なガイドラインで警告したほどです。(American Statistical Association [2016], #4で議論)
例えば、信頼区間95%では、こういった一連の動作を20回繰り返せば、大体誤った良い結果は見つかるのです。
解決策: 特徴量の重要度分析
例えば、行列の組として$(X,y)$が与えられていたとします。$X$は特定の金融商品による特徴量または説明変数で、$y$は目的変数だとします。
私たちは、分類器を$(X,y)$にフィッティングさせて、交差検証によって一般的な誤差関数を評価することが出来ます。
ここでは、良い結果が得られたとしましょう。
次の問題として、どのような特徴量がパフォーマンスに貢献しているかです。
私たちは新しい特徴量を追加して、分類器の予測力を向上させることが出来るかもしれないし、予測に対してノイズを与えるだけの特徴量を取り除くことも出来るかもしれません。
最も重要なことは、所謂ブラックボックスを開けて、特徴量の重要度を理解することです。
無くてはならない情報が何であるかを理解したときに、私たちは分類器によって発見された規則性について見解を得ることが出来ます。
これは、ブラックボックス神話が機械学習の懐疑性によって誇張されたものである理由の一つでもあります。
アルゴリズムは私たち無しで学習し、ブラックボックス化のプロセスへ直行しますが、だからと言って、私たちはアルゴリズムが何を発見したのかについて見れないということではないのです。
私たちが重要な特徴量を見つけたら、私たちはそれに対してより多くの実験を行うことが出来ます。
ここから調査出来る項目の例を挙げます。
- これらの特徴量は常に重要なのか、それとも特定の場面においてのみなのか。
- 何が重要度の変化の引き金になっているのか、そのようなレジームを予測可能に出来るか。
- これらの重要な特徴量は他の金融商品に対しても関係があるのか。他のアセットクラスとは?
- 全ての金融商品で最も関係のある特徴量は?どういった特徴量の部分集合が投資ユニバースにおいて最も関係を持つのか。
これらを調査することは、誤ったバックテストのサイクルを行うよりも遥かに生産的です。
結論を言います。
特徴量の重要度ことがリサーチツールであって、バックテストはそうではありません。
書評:ランダムフォレスト等のアンサンブルモデルを用いて特徴量の重要度を見るというのは分かるのですが、ただ、この手法も若干危ないと思っておりまして、特徴量の重要度は同じような特徴量があると重要度が落ちるという性質があります。つまり、特徴量同士が互いに独立でない限り、精確な重要度は測れないのです。なので、個人的にはピアソン相関係数やスピアマンの順位相関係数等を用いて一つ一つの特徴量が将来価格変化率へのインパクトを見ることが一番確実かと思います。(これを業界用語で情報係数(Information Coefficient)と呼びます。)
#3 時間サンプリング
整理されていないデータに対して機械学習アルゴリズムを応用する為には、私たちはそのデータを変換し、価値のある情報を抽出し、一般的な形式で保存する必要があります。ほとんどの機械学習アルゴリズムは、抽出されたデータのテーブル形式を仮定しています。金融の実務家は往々にしてこれらのテーブルの行を**バー、足(bars)**と呼びます。
恐らく時間足は実務家や研究者のどちらにとっても最も人気でしょうが、これを避けるべき理由が二つほどあります。
一つ目は、市場は一定の時間間隔で情報を与えていないということです。例えば、市場がオープンした時は、昼間よりかなり活発です。
生物学的に見ても、人が太陽の周期に合わせて一日の活動を行うということは普通です。
しかし、今日における市場は人々があまり干渉しないアルゴリズムによって営業されています。CPUの稼働周期は、太陽よりも時間間隔に影響しています。
つまり、時間バーは、市場があまり活発でないときは、オーバーサンプリングし、活発であるときは、アンダーサンプリングします。
二つ目は、時間サンプリングは往々にして微妙な統計的に性質を示します。例えば、系列相関、分散不均一性、非正規化されたリターンです。((Easley, López de Prado, and O’Hara [2012]))
GARCHモデルは、この誤ったサンプリングによる分散不均一性を対処するために開発されました。
解決策: 出来高時計
問題で話したように、投資活動を時間でサンプリングすると二つの問題が生じます。そして、それらを防ぐことは可能です。
このアプローチは、出来高時計(Volume Clock)とも呼ばれています(Easley, López de Prado, and O’Hara [2013])。
例えば、*ドルバー(dollar bars)*は観測値をある一定額(例えば100万ドル)区切りでサンプリングします。ここでいうドルというのは、法定通貨という意味で、株式を売買するときにおけるクオート・カレンシーです。(TPX/JPYならJPYです)
※円建てでもYen barsとは言わず、dollar barsと呼びます。
ドルバーを用いる理由についていくつか紹介しましょう。
一つ目は、ある期間において、株価の動きを100%理解したいとしましょう。最後の期間に1000ドル分の株を売却したい場合は、その分の株式を最初の期間に購入しないといけません。言い換えると、取引する株数は実際に取引される価値の関数であります。
つまり、1000ドル分のドルバーにすると、常に1000ドル分売り買いしたときの価格になります。
特に価格が十分に変動するときは、ドルバーは、ティックやボリュームバーよりも理にかなっています。
また経験的にもこのポイントを支持出来ます。
例えば私たちがE-mini S&P500のティックバーと出来高バーを計算したとして、バーの本数は年によってバラつきます。
このバラつきは、ドルバーに直せば、本数の変動の範囲やスピードを抑えることが出来ます。
二つ目は、ドルバーをより興味深くしているのは、コーポレートアクションの結果として株の発行済み株式数が何度も変化することです。
分割と株式併合で調整した後でも、新株の発行や購入や既存の株式を取り戻すなど、ティックと出来高の量に影響を与えるアクションがあります(2008年の大不況以来の一般的な慣行となっています)。
ドルバーはこういったアクションに対してはロバストです。更に、期間によってバーのサイズが異なるときにそれでもバーをサンプリングしたいとしましょう。このとき、株式のケースですが、バーのサイズは浮動株の時価総額に応じて動的に調整出来ます。債券であれば、発行済み債務の残高です。
より洗練されたタイプのバーがあり、これらは非対称情報の到着の関数として観測値をサンプリングします。
この内容はこの記事の範囲を超えておりますが、興味がある方は*LópezdePrado[2018]*の第2章を参照してくださいませ。
書評: 時間サンプリングについて悪いように書かれていますが、株式市場や為替市場では、一定時刻に証券会社や銀行のオペレーションによって市場が規則的になることもあるため、一概に時間によるサンプリングが悪いとは言えない気がします。また、時間によるサンプリングですと、マルチアセットを比較するときにも便利です。売買代金によってサンプリングする場合は、アセットクラスによって大幅にバーの数が変わり、正直比較出来ません。つまり、価格変化率を見るにしても、日経225の上位銘柄を一億円でリサンプリングした場合とマザーズの銘柄を一億円でリサンプリングした場合は、意味が全く異なるのです。銘柄に応じてサンプリング手法を変えるというのは難易度が高い上に距離がバラバラなので、単一資産のみを予測する場合のみ有効である気がします。また、インダイレクトモデルのように、一資産の価格を予測する際に、他の資産の価格を入力として使用する際も、将来の情報を含まないように注意する必要があります。
#4 整数次差分(Integer Differentiation)
金融では、非定常時系列を見つけるのが一般的です。これらのシリーズを非定常にしているのは、記憶の存在です。推論分析を実行するために、研究者は、価格のリターン(または対数価格の変化)、利回りの変化、またはボラティリティの変化などの不変の過程を処理する必要があります。これらのデータ変換により、元のシリーズからすべてのメモリが削除されますが、シリーズは静止します(Alexander [2001]、第11章)。定常性は推論の目的に必要なプロパティですが、信号処理では、メモリがモデルの予測力の基礎であるため、すべてのメモリを消去することはめったにありません。たとえば、均衡(定常)モデルでは、予測を生成するために、価格過程が長期の期待値からどれだけ離れているかを評価するためのメモリが必要です。ジレンマは、リターンは定常的であるがメモリがなく、価格にはメモリがあるが非定常的であるということです。ここで疑問が生じます:可能な限り多くのメモリを保持しながら価格系列を定常化させる最小の差別化量はどれくらいですか?
※補足: 価格の変化率を$Y_t = (X_t - X_{t-1})/X_{t-1}$としますと、$Y_t$と$Y_{t-1}$は基本的に独立となってしまいます。かといって、$X_t$と$X_{t-1}$は情報量は全く消えませんが、定常的ではないので予測に用いることは出来ません。ここで、より上手な変換で情報を最大限キープしつつも、お互いが独立となるような変数変換はないのかについて探ることがここでの目標となります。
教師あり学習アルゴリズムは通常、定常的な特徴量を必要とします。その理由は、それまで見えなかった(ラベルのない)観測をラベル付きの例の集まりにマッピングし、それらの情報から新しい観測のラベルを推測する必要があるためです。特徴が定常的でない場合、新しい観測値を多数の既知の例にマッピングすることはできません。しかし、定常性は予測力を保証しません。定常性は、MLアルゴリズムの高性能にとって必要十分条件ではありません。問題は、定常性とメモリの間にトレードオフがあることです。微分によってシリーズを常に静止させることができますが、一部のメモリを消去するという犠牲が伴い、MLアルゴリズムの予測目的が無効になります。
リターンは、他の多くの可能性の中で、価格変換の一種にすぎません(ほとんどの場合、最適ではありません)。共和分法の重要性の一部は、メモリを使用して系列をモデル化する機能です。しかし、なぜ微分がゼロの特定のケースが最良の結果をもたらすのでしょうか?ゼロ微分は、1ステップ微分と同じくらい恣意的です。これらの2つの極値の間には広い領域があります(一方では完全に微分された系列であり、他方ではゼロで微分された系列です)。
解決策: 分数次変換(Fractional Differentiation)
事実上すべての金融時系列の文献は、整数変換によって非定常系列を定常にするという前提に基づいています(例については*Hamilton [1994]*を参照)。しかし、なぜ整数1の微分(対数価格のリターンの計算に使用されるものなど)が最適なのでしょうか?
分数次変換はリターンの非整数$d$次差分の概念を一般化してくれます($d > 0$)。ここで観測値の系列を$\{x_t \}_{t=1,...,T}$が与えられているとしまして、時刻$t$における$d$次分数次変換は
\displaystyle \hat{x_t} = \sum_{k=0}^{\infty} \omega_{k}x_{t-k}
と与えられます。ただし、$\omega_0 = 1$で$\omega_k = - \omega_{k-1}\frac{d-k+1}{k}$です。
上の方程式の導出と意味については、*LópezdePrado [2018]*の第5章を参照してください。
例えば、$d=0$であれば、$\omega_0 = 1$で0以外の$k$で$\omega_k = 0$となります。これは、系列の生値データをそのまま使っている(恒等変換)です。次に$d=1$の場合ですが、これは、$\omega_0 = 1, \omega_1 = -1, \omega_k = 0 (k \neq 0, 1)$となります。これは、対数価格における標準的な一次整数差分となります(要するに価格変化率みたいなことです)ここでは、メモリを保持させつつも、定常性を持たせるための最適な$d \in [0, 1]$を探すことが目標です。
E-mini S&P500の対数価格の系列があるとします。元の系列($d=0$)でのADF検定の統計量は-.3387であり、この値では、95%の信頼度で単位根の帰無仮説を棄却できません(臨界値は-2.8623です)。ただし、$d= .4$のFracDiff系列で計算されたADF統計の値は-3.2733であり、95%を超える信頼水準で帰無仮説を棄却できます。さらに、元の系列と$d= .4$のFracDiff系列の間の相関は非常に高く、約0.995であり、ほとんどのメモリがまだ保持されていることを示しています。図表4は、𝑑のさまざまな値について、ADF統計と元の系列との相関をプロットしています。対照的に、$d = 1$(標準リターン)では、FracDiff系列のADF統計は-46.9114であり、元の系列との相関はわずか0.05です。言い換えると、標準リターンは、定常性を達成するために必要なよりもはるかに多くのメモリを消去するという意味で、系列を過度に差別化します。
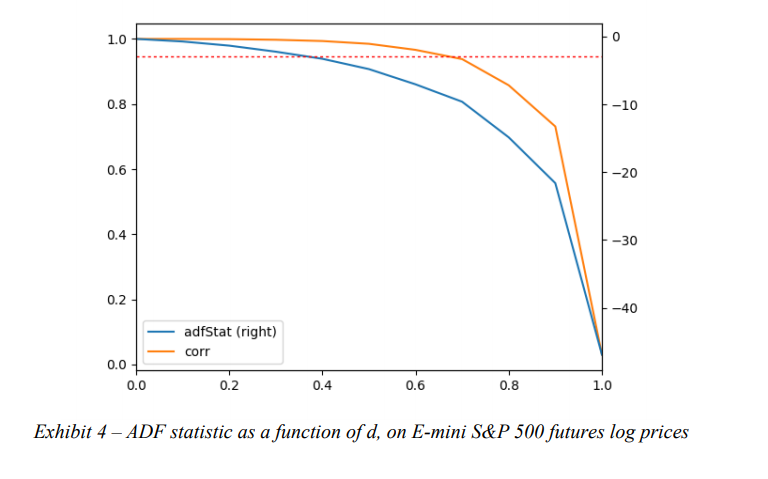
(参照元: THE 10 REASONS MOST MACHINE LEARNING FUNDS FAIL, Marcos López de Prado [2018])
上記の調査結果は、E-mini S&P500の対数価格に固有のものではありません。 *López de Prado[2018]*は、世界中で取引されている87の最も流動性の高い先物契約のうち、すべての対数価格が$d < .6$で定常性を達成し、実際、大多数が$d < .3$で定常性を達成していることを示しています。結論として、何十年もの間、ほとんどの実証研究は、メモリが不必要に消去された系列で機能してきました。これが危険な慣行である理由は、メモリのない系列を適合させると、偽のパターン、誤った発見につながる可能性が高いためです。ちなみに、この時系列の過度の差別化は、効率的市場仮説が依然として学界の間で非常に普及している理由を説明している可能性があります。記憶がなければ、系列は予測できず、研究者は市場が予測できないという誤った結論を引き出す可能性があります。
**書評:**よくある株価データをそのまま用いて株価を予測出来ないかという問題に対して、定常的ではないから出来ないというのが従来の回答だったと思いますが、これは、そういった株価に対して特定の変換を行い、従来の株価との相関係数を高く維持しつつも、定常性を持たせてモデルが学習しやすいようにしています。私も時々こういった変換を行って調査することがあるので、皆さんも是非試してみてください。
#5 固定期間ホライズン法
**問題点:**金融に関しては、事実上すべてのML関連の学術誌は、固定期間ホライズン法を使用して観測値にラベルを付けます。
ここでは簡単に解説します。時刻$t$における観測値を$x_t$としたら、$n$期間後の将来リターン$r_{t+n, t}$は$r_{t+n, t} = x_{t+n}/x_{t}-1$と与えられます。これに閾値$\tau$を設けて、整数ラベル$y_i$を$r < -\tau$なら$y_i = -1$, $|r| \leq \tau$なら$y_i = 0$, $r > \tau$なら$y_i = 1$というようなラベリング手法です。
具体的なラベル付けの方法についてはTHE 10 REASONS MOST MACHINE LEARNING FUNDS FAIL, Marcos López de Prado [2018]のPITFALL #5を参照してください。
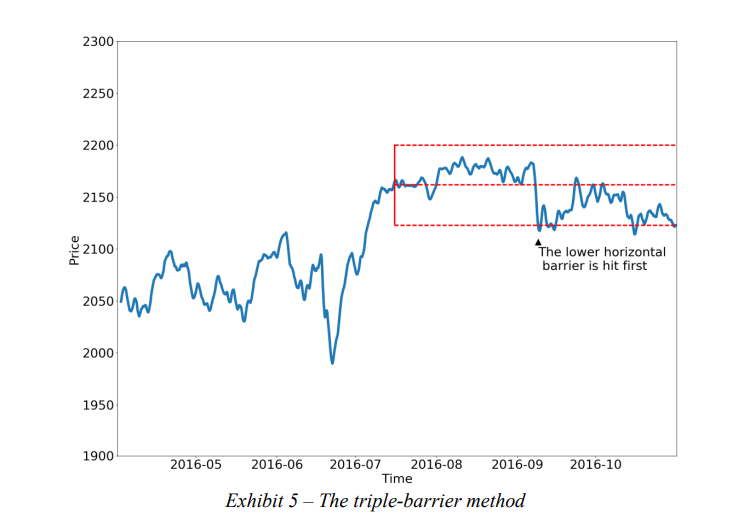
**解決策:**より良いアプローチは、ポジションの終了をトリガーする条件に従って観測にラベルを付けることです。これを達成する1つの方法を見てみましょう。まず、2つの水平バリアと1つの垂直バリアを設定します。 2つの水平方向の障壁は、利益確定とストップロスの制限によって定義されます。これらは、推定ボラティリティ(実現または暗黙的)の動的関数です。 3番目のバリアは、ポジションが取得されてから経過したバーの数で定義されます(アクティビティベースであり、固定時間の有効期限制限ではありません)。上部の水平バリアに最初に触れた場合、観測値に1のラベルを付けます。下部の水平バリアに最初に触れた場合、観測値に-1のラベルを付けます。垂直方向の障壁に最初に触れる場合、2つの選択肢があります。リターンのサインまたは0です。制限内で利益または損失を実現するという点で私は個人的に前者を好みますが、0がより効果的かどうかを調べる必要があります。
バリアをまとめますと次の通りになります。
・水平バリア: 利益確定とストップロス(推定ボラティリティの動的関数、固定でも良い)
・垂直バリア: 最大保有期間
**書評:**究極は1ステップ先のリターンを完全に予測することですが、コスト等もあって、仮に完全に予測できたとしても手数料でマイナスになることはよくあります。なので、マーケットの手数料に応じて、この幅を調整する等すればコスト削減にもなります。また、ストップロスが定められていることから、リスク管理もしやすいのでそういった意味でもおすすめのラベル付け手法だと言えます。
#6 サイドとサイズを同時に学習
**問題点:**金融MLの一般的な過ちは、ポジションのサイドとサイズを同時に学習する必要がある複雑すぎるモデルを構築することです。これが一般的に間違いである理由を議論させてください。 「サイド」決定(購入するか販売するか)は、特徴量行列によって特徴付けられる、特定の一連の状況下での証券の公正価値に関係する厳密に基本的な決定です。ただし、「サイズ」の決定はリスク管理の決定です。それはあなたのリスク予算、資金調達能力、そして非常に重要なことに、「サイド」の決定に対するあなたの自信と関係があります。これらの2つの異なる決定を1つのモデルに結合する必要はありません。関連する追加の複雑さは保証されていません。
実際には、2つのモデルを作成する方がよい場合が多く、1つはサイドを予測し、もう1つはポジションのサイズを予測します。プライマリモデルの目標は、ポジションのリターンの符号を予測することです。セカンダリモデルの目標は、一次モデルの予測の精度を予測することです。言い換えれば、セカンダリモデルは市場を予測しようとするのではなく、一次モデルの弱点から学ぶことを試みます。また、プライマリモデルは取引の意思決定を行うものと考えることができますが、セカンダリモデルはリスク管理の意思決定を行うものと考えることができます。
解決策:メタラベリング
メタラベリングは、より高いF1スコアを達成したい場合に特に役立ちます。まず、精度が特に高くなくても、高い再現率を実現するプライマリモデルを構築します(たとえば、市場の反発を予測する場合)。次に、結果(ポジティブまたはネガティブ)に応じてプライマリモデルの賭けにラベルを付けることにより、精度の低さを修正します。これらのメタラベルの目標は、誤検知を除外することでF1スコアを上げることです。誤検知は、プライマリモデルによってすでに識別されています。別の言い方をすれば、セカンダリMLアルゴリズムの役割は、プライマリ(サイドデシジョン)モデルからのポジティブが真であるか偽であるかを判断することです。賭けの機会を考え出すことはその目的ではありません。その目的は、提示された機会を実行するか、渡すかを決定することです。
メタラベリングは、4つの追加の理由から、兵器庫にある非常に強力なツールとなります。
- まず、MLアルゴリズムはブラックボックスとして批判されることがよくあります。メタラベリングを使用すると、ホワイトボックスの上にMLシステムを構築できます(経済理論に基づいた基本モデルのように)。基本モデルをMLモデルに変換するこの機能により、メタラベリングは「クオンタメンタル(quantamental) 最新のヘッジファンドの手法は「クオンタメンタル」, Bloomberg News」企業にとって特に有用になるはずです。
- 第2に、メタラベリングを適用する場合、MLは賭けのサイドを決定せず、サイズのみを決定するため、過剰適合の影響は制限されます。全体的な戦略行動を制御する単一のモデルまたはパラメーターの組み合わせはありません。
- 第三に、サイド予測をサイズ予測から切り離すことにより、メタラベリングは洗練された戦略構造を可能にします。たとえば、ラリーを推進する機能は、売り切りを推進する機能とは異なる場合があることを考慮してください。その場合、プライマリモデルの買い推奨に基づいてロングポジション専用のML戦略を開発し、まったく異なるプライマリモデルの売り推奨に基づいてショートポジション専用のML戦略を開発することができます。
- 第四に、小さな賭けで高い精度を達成し、大きな賭けで低い精度を達成することはあなたを台無しにするでしょう。良い機会を特定することと同じくらい重要なのは、それらを適切にサイズ設定することです。したがって、その重要な決定(サイズ設定)を正しく行うことに専念するMLアルゴリズムを開発することは理にかなっています。私の経験では、メタラベリングMLモデルは、標準のラベリングモデルよりも堅牢で信頼性の高い結果を提供できます。
#7 非iid標本の重み付け
**問題点:**ほとんどの非金融ML研究者は、観察結果がIID過程から引き出されていると想定できます。たとえば、多数の患者から血液サンプルを取得し、そのコレステロールを測定することができます。もちろん、さまざまな根本的な共通の要因により、コレステロール分布の平均と標準偏差がシフトしますが、サンプルは依然として独立しています。被験者ごとに1つの観測値があります。
あなたがそれらの血液サンプルを採取し、あなたの研究室の誰かが各チューブからその右側の次の9本のチューブに血液をこぼしたとします。つまり、チューブ10には、患者10の血液だけでなく、患者1〜9の血液も含まれます。チューブ11には、患者11の血液だけでなく、患者2〜10の血液も含まれます。次に、各患者のコレステロール値を確実に知ることなく、高コレステロールを予測する機能(食事、運動、年齢など)を決定する必要があります。
この「こぼれたサンプル」の問題は、金融MLで直面する課題と同等です。ここで、(1)ラベルは結果によって決定されます。 (2)結果は複数の観察にわたって決定されます。 (3)ラベルは時間的に重複しているため、観察された特徴がどのような影響を及ぼしたかを特定することはできません。
解決策: 独自の重み付けと順次ブートストラップ
二つのラベル$y_i$と$y_j$が両方が少なくとも1つの共通リターンの関数$r_{t-1, t} = p_t/p_{t-1}-1$である場合、観測点$t$で同時発生的であるとします。
私たちは観測値の独自性の次数を次の表のように評価することが出来ます。
$1_{t,i}$を$1_{t, i} = I(r_{t_{i, 1}, t_{i, 0}} = r_{t, t-1})$とします。
-
- それぞれの観測点$t=1,...,T$で二値の配列$\{1_{t,i} \}_{i=1,...,l} \in \{0, 1\}^l$があるとします。
- 2.条件を満たしたラベルの数$c_t = \sum_{i=1}^l 1_{t,i}$を計算します。
- 3.ラベル$i$の独自性を$u_{t, i} = 1_{t,i}c_t^{-1}$とします。
- 4.ラベル$i$の平均的な独自性は、ラベルの存続期間中の平均$t_{t,i}$で、$\overline{u_i} = (\sum_{t=1}^T u_{t,i})/c_t$。
- 5.標本の重みはイベントの存続期間$[t_{i, 0}, t_{i, 1}]$上でのリターンの和として定義します。
\displaystyle \tilde{w_i} = |\sum_{t=t_{i,0}}^{t_{i,1}} \frac{r_{t-1, t}}{c_t}|
\displaystyle w_i = \tilde{w_i}I(\sum_{t=t_{i,0}}^{t_{i,1}} \tilde{w}_j)^{-1}
この方法の理論的根拠は、観測値に一意に帰することができる絶対対数リターンの関数として観測値に重みを付けることです。 López de Prado[2018]の第4章では、この重み付けスキームを使用して、一意性の低いサンプルをブートストラップする方法を示しています。一般的な概念は、すべてのサンプルを同時に描画するのではなく、サンプルを順番に描画することです。各ステップで、一意性の高い観測値を描画する確率を高め、一意性の低い観測値を描画する確率を減らします。モンテカルロ実験は、順次ブートストラップがサンプルの平均一意性を大幅に向上させ、モデルにより多くの情報を注入し、「こぼれたサンプル」効果を低減できることを示しています。
#8 交差検証の将来情報漏洩
**問題点:**k-fold交差検証が金融で失敗する理由の1つは、観測値がIID過程から引き出されると想定できないためです。リークは、トレーニングセットにテストセットにも表示される情報が含まれている場合に発生します。重複するデータ上に形成されるラベル$Y$に関連付けられている系列相関のある特徴量$X$について考えてみます。(1)系列相関のため、$X_t \approx X_{t+1}$; (2)ラベルは重複するデータポイントから派生しているため、$Y_t \approx Y_{t+1}$。次に、$t$と$t + 1$を異なるセットに配置すると、情報がリークします。分類器が最初に$(X_t、Y_t)$でトレーニングされ、次に観測された$X_{t+1}$に基づいて$E[Y_t+1]$を予測するように求められた場合、この分類器は$Y_{t+ 1} =E[Y_t+1]$を達成する可能性が高くなります。 たとえ、$X$が無関係な特徴量であっても。無関係な特徴量が存在する場合、リークは誤った発見につながります。
解決策:パージングとエンバーゴ
細かく説明すると長くなるので、大分端折りますが、テストデータのデータの最初の部分と最後の部分を取り除けば良いです。どれくらい取り除くかと言いますと、最初の部分に関しましては、予測ホライズン分(一週間後予測なら、一週間分取り除く)、最後の部分に関しましては、特徴量として移動平均線等ある程度計算期間を要する場合、最長の計算期間(例えば1か月移動平均線の場合1か月)分取り除く必要があります。
特に本論文の著者は、ウォークフォワード法に反対しているので、テストデータの前後には細心の注意を払う必要があります。
#9 ウォークフォワード・バックテスト
問題点: 文献で最も一般的なバックテスト方法は、ウォークフォワード(WF)アプローチです。 WFは、戦略が過去にどのように実行されたかのヒストリカルシミュレーションです。各戦略の決定は、その決定より前の観察に基づいています。 WFには2つの重要な利点があります。(1)WFには明確な歴史的解釈があります。そのパフォーマンスは、ペーパートレーディングと調和させることができます。 (2)歴史はフィルトレーションです。したがって、トレーリングデータを使用すると、パージが適切に実装されている限り、テストセットがアウトオブサンプル(リークなし)であることが保証されます。
WFには、3つの大きな欠点があります。
- 最初に、単一のシナリオがテストされ(ヒストリカル・パス)、簡単に過学習する可能性があります(Bailey et al. [2014])。
- 第2に、結果はデータポイントの特定の配列によってバイアスされる可能性があるため、WFは必ずしも将来のパフォーマンスを表すとは限りません。 WF法の支持者は通常、過去を予測すると過度に楽観的なパフォーマンスの見積もりにつながると主張します。それでも、観測の配列を逆にしてアウトパフォームしたモデルを当てはめると、WFバックテストのパフォーマンスが低下することがよくあります。実際に、ウォークフォワードバックテストをオーバーフィットするのはウォークバックバックバックテストをオーバーフィットするのと同じくらい簡単であり、観測の順序を変更すると一貫性のない結果が得られるという事実は、そのオーバーフィットの証拠です。 WFの支持者が正しければ、ウォークバックバックテストがウォークフォワードのバックテストよりも体系的に優れていることを確認する必要があります。そうではないので、WFを支持する主な議論はかなり弱いです。この2番目の不利な点を明確にするために、2007年1月1日からS&P 500データのWFでバックテストされた株式戦略を想定します。2009年3月15日まで、ラリーとセルオフの組み合わせにより、マーケットニュートラルになるように戦略がトレーニングされます。すべてのポジションの信頼度が低い。その後、ロングラリーがデータセットを支配し、2017年1月1日までに、買いの予測が売りの予測よりも優先されます。 2017年1月1日から2007年1月1日まで、情報を逆方向に再生した場合、パフォーマンスは大きく異なります(長いラリーとそれに続く急激な売り切り)。特定の配列を悪用することにより、WFによって選択された戦略は、私たちに大失敗をもたらす可能性があります。
- WFの3番目の欠点は、最初の決定がサンプル全体のより小さな部分で行われることです。ウォームアップ期間が設定されている場合でも、ほとんどの情報は決定のごく一部でのみ使用されます。
解決策: 組み合わせ交差検証(COMBINATORIAL PURGED CROSS-VALIDATION)
これは私が嚙み砕いて説明しますが、まずデータを均一に$n$個のバスケットを作ります。そして、その中から$k$個を選びテスト期間、残りの$n-k$個を訓練期間とします。
テスト期間と訓練期間の組み合わせの個数は当然$n \choose k$になります。
ここで、テスト期間の前後では情報漏洩のリスクがあったので、一部のデータを取り除きます。これをパージングと呼びます。
それぞれのテスト期間と訓練期間に対して、訓練とテストを繰り返すアプローチになります。
#10 バックテストの過学習
問題点: 私たちが投資戦略を選ぶときは基本的に良いバックテストを持つ戦略を選びます。この結果、何度もバックテストを行い、良い結果が出た戦略を使用しようとします。問題なのは、こういった手法で選んだ投資戦略を本当に信用できるかどうかです。
解決策:デフレシャープレシオ(Deflated Sharpe Ratio)
私の記事でも解説していたので、詳しくはこちらをご覧ください。
そろそろシャープレシオに蹴りをつけようか。
全体の感想
問題点は非常に分かりやすいものも多かったと思いますが、解決策が非常に難解であるものもあり、私が自分でより簡潔に説明できる部分は私の言葉で補足させていただきましたが、簡潔に説明できない部分は私自身もちゃんと理解出来ていない可能性があります。ファインマンさんも言っていた「簡単な言葉で説明できないならあなたは理解していない」という言葉は今回身に染みて感じた次第です。ここまで長文になるとは思っておりませんでした。
個人的に一番難解に感じたのは#6,#7でここら辺は私ももう少し力を入れて勉強しようかと思いました。また、本論文を読んでいて、ファイナンス機械学習と同じようなストーリーも多かったので、ファイナンス機械学習を見直しましたら、やはり本論文が起源でした。ファイナンス機械学習は400ページ近く書かれてありますが、そういった意味では、この記事の内容は大分短いのかもしれません。
感想も長くなりましたが、興味ある部分だけでも読んで、少しでもお役に立てれば幸いです。
参考文献
- Alexander, C. (2001): Market Models. 1st edition, John Wiley & Sons.
- American Statistical Association (2016): “Ethical guidelines for statistical practice.” Committee
on Professional Ethics of the American Statistical Association (April). Available at
http://www.amstat.org/asa/files/pdfs/EthicalGuidelines.pdf - Bailey, D., J. Borwein, M. López de Prado, and J. Zhu (2014): “Pseudo-mathematics and
financial charlatanism: The effects of backtest overfitting on out-of-sample performance.”
Notices of the American Mathematical Society, Vol. 61, No. 5, pp. 458–471. Available at
http://ssrn.com/abstract=2308659 - Bailey, D. and M. López de Prado (2012): “The Sharpe ratio efficient frontier.” Journal of Risk,
Vol. 15, No. 2, pp. 3–44. - Bailey, D. and M. López de Prado (2014): “The deflated Sharpe ratio: Correcting for selection
bias, backtest overfitting and non-normality.” Journal of Portfolio Management, Vol. 40, No. 5,
pp. 94-107.* - Calkin, N. and M. López de Prado (2014a): “Stochastic flow diagrams.” Algorithmic Finance,
Vol. 3, No. 1, pp. 21–42. - Calkin, N. and M. López de Prado (2014b): “The topology of macro financial flows: An
application of stochastic flow diagrams.” Algorithmic Finance, Vol. 3, No. 1, pp. 43–85. - Easley, D., M. López de Prado, and M. O’Hara (2011): “The volume clock: Insights into the high
frequency paradigm.” Journal of Portfolio Management, Vol. 37, No. 2, pp. 118–128. - Easley, D., M. López de Prado, and M. O’Hara (2012): “Flow toxicity and liquidity in a high
frequency world.” Review of Financial Studies, Vol. 25, No. 5, pp. 1457–1493. - Easley, D., M. López de Prado, and M. O’Hara (2013): High Frequency Trading: New Realities
for Traders, Markets and Regulators. 1st edition, Risk Books. - Hamilton, J. (1994): Time Series Analysis, 1st edition. Princeton University Press.
- López de Prado, M. (2014): “Quantitative meta-strategies.” Practical Applications, Institutional
Investor Journals, Vol. 2, No. 3, pp. 1–3. - López de Prado, M. (2018): Advances in Financial Machine Learning. 1st edition, Wiley.
https://www.amazon.com/dp/1119482089 - Stigler, Stephen M. (1981): “Gauss and the invention of least squares.” Annals of Statistics, Vol.
9, No. 3, pp. 465–474. - López de Prado, M. (2019): 金融市場分析を変える機械学習アルゴリズムの理論と実践