モチベーション
この記事では、価格系列がトレンドないし平均回帰性の発見に役立つ統計的手法について紹介します。
これを発見する目的は、そういった振る舞いに対して、モメンタムないし平均回帰の投資戦略を取ることが出来るからです。
ここでは、実際にコーディングも含めて解説していこうと思います。
イントロダクション
定量投資における重要なコンセプトの一つは平均回帰です。これは、時系列データがヒストリカルの平均値に回帰する傾向を示すということです。
平均回帰戦略は統計的裁定取引を行うクオンツ系ヘッジファンドにとっても非常に大事です。
時系列が平均回帰するかどうかを見つける基本的なアイデアは、統計的な検定を用いて、時系列データの振る舞いがランダムウォークであるかどうかを判別することにあります。
時系列データがランダムウォークであるとは、次の時点における株価の方向がそれまでの動きに対して完全に独立であることです。
コイントスに関するよくある問題で、10回連続で表だったときに、次も表である確率は?という問いは、コイントスの表の確率が50%であれば次も50%です。
つまり、過去の出来事に対して記憶していないということです。
しかし、平均回帰性を持つ時系列データは違います。次の時刻における価格変化率は今の株価に比例するのです。
正確に言うと、ヒストリカルの平均値と現在の価格の差と比例するのです。
数学的には、こういった時系列データはOrnstein-Uhlenbeck過程(以下OU過程)と呼びます。
時系列データが統計的にOU過程であるような振る舞いとすれば私たちはそれからそれに対して投資戦略を考えることが出来ます。
この記事のゴールは平均回帰性を検定するために必要な統計的アプローチとPythonのstatsmodelsを使用してこれら検定を実装することです。
特に、定常性のコンセプトについて学び、それに対して検定出来ることです。
上で述べたように、連続的な平均回帰性を持つ時系列データは以下のようなOU確率微分方程式で表すことが出来ます。
dx_t = \theta(\mu - x_t)dt + \sigma dW_t
ただし、$\theta$は平均への回帰率、$\mu$は確率過程の平均値、$\sigma$は確率過程の標準偏差、$W_t$はウィーナー過程またはブラウン運動とします。
この方程式は、価格の変化が平均値と現在価格の差に比例することを示しています。
ここから、この方程式を使って Augumented Dickey-Fuller検定(以下、ADF検定)を定義します。
Augumented Dickey-Fuler (ADF) 検定
ADF検定は価格系列が平均回帰性を持つかどうかに対して行われる統計的検定手法です。特に、イントロダクションで述べたOU過程に従うかどうかを検定します。
数学的には、ADF検定は、自己回帰する時系列データに対する単位根の存在を検定するためにあります。
では、時系列データをモデリングしましょう。
\Delta{y_t} = \alpha + \beta t + \gamma y_{t-1} + \delta_1 \Delta{y_{t-1}} + ... + \delta_{p-1}\Delta{y_{t-p+1}}+\epsilon_t
ただし、$\alpha$は定数、$\beta$は一時的なトレンドの係数、$Delta{y_t} = y(t) - y(t-1)$とします。
この時系列データを$p$次線形ラグモデル(linear lag model of order p)と呼びます。
このモデルは、価格変化が定数と時刻と$p$個前までの価格変化に比例することを示します。
ADFの仮説検定は、$\gamma = 0$であるかどうかを確認し、これは$\alpha = \beta = 0$のときにこの系列がランダムウォークであることを示唆しています。
つまり、帰無仮説$\gamma = 0$であることを検定します。
もし、$\gamma = 0$という仮説が棄却されれば、次の株価の動きは現在価格に対して比例することを意味し、ランダムウォークではない可能性が高いという結論が得られます。
では、どのようにしてADF検定を行うのでしょうか?
- 検定統計量$DF_{\tau}$を計算します。これは、帰無仮説を棄却する決定を行うために用います。
- DickeyとFullerから計算された統計検定量の分布を用いて、棄却限界値を求め、帰無仮説の棄却の決定を行います。
さて、統計検定量($DF_{\tau}$)から計算を始めましょう。これは、標本の比例定数$\hat{\gamma}$を標本の比例定数の標準偏差で割ったものです。
DF_{\tau} = \frac{\hat{\gamma}}{SE(\hat{\gamma})}
検定統計量が計算出来たので、次はDickeyとFullerから計算された統計検定量の分布を用いて、任意の百分位に対して棄却限界値を求めます。
因みに統計検定量は負の値なので、棄却限界値に対して十分であるためには、統計検定量はより小さくないといけません。
トレーダーにとっての実務上における重要な問題は、価格系列から計算した任意の長期ドリフトは短期ドリフトに対してかなり小さくなるため、ドリフトを0と仮定($\beta = 0$)することが多いです。
今回は$p$次ラグモデルを仮定しているため、$p$を特定の値で定義しなければならない。投資の調査においては、$p=1$で十分帰無仮説を棄却出来ることが多いです。
しかし、技術的には、これはADFに基づいたトレーディングモデルにパラメーターを代入するときに限った話なので、一般的な話ではなく、注意が必要です。
では、計算していきましょう。
今回は、pandasとstatsmodelsのライブラリを用いて、ADF検定を行います。
from __future__ import print_function
import statsmodels.tsa.stattools as ts
from datetime import datetime
from pandas_datareader import DataReader
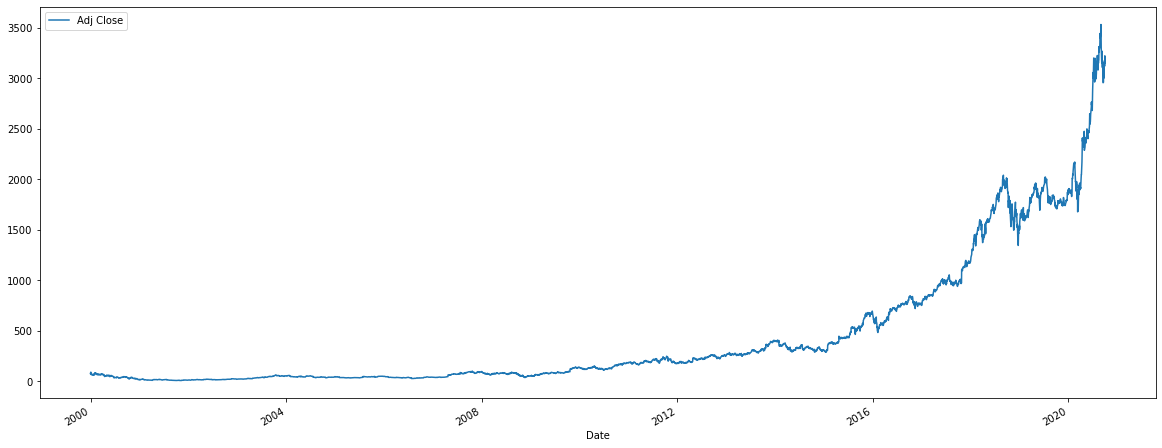
amzn = DataReader("AMZN", "yahoo", datetime(2000, 1, 1), datetime(2020, 10, 4))
ts.adfuller(amzn["Adj Close"], 1)
'''output
(4.179160350494452,
1.0,
1,
5221,
{'1%': -3.4316031158795095,
'5%': -2.862093746873135,
'10%': -2.5670647592452664},
43914.24940744905)
'''
(図:Amazonの株価:調整済み終値)
※注意: pandas.io.dataは既に使用できないため、pandas_datareaderを用いてYahoo FinanceからOHLCVデータを取得しています。
本コードで、Amazon株に対するADF検定の出力を計算出来ました。
出力について説明します(詳細はstatsmodels.tsa.stattools.adfuller)
- 一番目:検定統計量
- 二番目:$p$値
- 三番目:使用したラグの数
- 四番目:サンプル数
- 五番目:検定統計量の棄却限界値
この系列では、検定統計量が正の値で、棄却限界値に全く到達出来ていないため、帰無仮説を棄却出来ませんでした。つまり、Amazon株は平均回帰するとは言えないということです。これは株価が幾何ブラウン運動ないしランダムウォークに従っているということです。
ADF検定に関する説明はここまでですが、平均回帰性を検定するその他手法についても紹介できればと思います。
定常性の検定
時系列データが 強力に定常的(strongly stationary)であるとは、同時確率分布が時刻または空間による変換に対して不変であることです。特に、トレーダーにとって重要なことは、確率過程の平均と分散が時間ないし空間方向で変わらない、すなわちトレンドがないということです。
定常性を持つ時系列データの重要な特徴は、価格が幾何ブラウン運動よりも初期値から拡散する速度が遅いということです。この拡散的な振る舞い率を測るためは、時系列データが平均回帰するかどうかを検定すれば良いです。
ここで、時系列の定常性を特徴づけるためにHurst Exponentを導入します。
Hurst Exponent
Hurst Exponentは系列が平均回帰するのか、それともランダムウォークなのか、それともトレンドがあるのかを見極めるのに役立つスカラー値を提供してくれます。
Hurst Exponentの計算の裏にあるアイデアは、対数価格の分散を用いて拡散的な振る舞い率を評価できることです。
任意の時刻のラグ$\tau$に対して、$\tau$の分散は以下のように与えられます。
\mbox{Var}(\tau) = \bigl<|\log(t+\tau) - \log(t)|^2 \bigl>
ただし、バスケット($\bigl<・ \bigl>$)は$t$に関する平均値とします。
幾何ブラウン運動と比較する為なので、幾何ブラウン運動のケースも考えます。幾何ブラウン運動の場合は、$\tau$が大きいとき、$\tau$の分散は$\tau$に比例します。
\bigl<|\log(t+\tau) - \log(t)|^2 \bigl> \sim \tau
もし、これに従わない系列を見つけた場合は、トレンドか平均回帰性を持つとします。重要な考え方は、自己相関を持つ確率過程に対しては、上の関係を満たさないからです。
ここで上の式を修正して、べき乗に$2H$を含ませますと、この$H$をHurst Exponent値を呼びます。
\bigl<|\log(t+\tau) - \log(t)|^2 \bigl> \sim \tau^{2H}
よって、$H=0.5$の場合は幾何ブラウン運動、$H \neq 0.5$ではトレンドか平均回帰性を持つとします。
特に、
- $H < 0.5$ : 時系列データが平均回帰性を持つ
- $H = 0.5$ : 時系列データが幾何ブラウン運動である
- $H > 0.5$ : 時系列データがトレンドを持つ
と考えます。
更に、Hurst Exponentの値の大きさはトレンド性や平均回帰性の程度をも表します。$H$が0付近なら、かなり平均回帰します。逆に$H$が1付近なら、かなりトレンドがあります。
上のADF検定で示したAmazonの系列に対して、Hurst Exponentを行ってみましょう。
from numpy import cumsum, log, polyfit, sqrt, std, subtract
from numpy.random import randn
import numpy as np
def hurst(ts):
lags = range(2, 100)
tau = [sqrt(std(subtract(np.array(ts[lag:]), np.array(ts[:-lag])))) for lag in lags]
poly = polyfit(log(lags), log(tau), 1)
return poly[0] * 2
N = 100000
INIT = 1000
gbm = log(cumsum(randn(N)) + INIT)
mr = log(randn(N) + INIT)
tr = log(cumsum(randn(N) + 1) + 1000)
print("Hurst(GBM) : %s" % hurst(gbm))
print("Hurst(MR) : %s" % hurst(mr))
print("Hurst(TR) : %s" % hurst(tr))
print("Hurst(AMZN): %s" % hurst(amzn["Adj Close"]))
"""output
Hurst(GBM) : 0.5009895191155147
Hurst(MR) : -0.00011676275965904795
Hurst(TR) : 0.9531094098903697
Hurst(AMZN): 0.5397101554176691
"""
ここでMRは平均回帰性を持つ系列、TRはトレンドを持つ系列、GBMは幾何ブラウン運動となります。
ここでAmazonはほとんど0.5付近で、GBMと似ているということになります。(ただし、少なくともサンプルでは。)
共和分
現実では、平均回帰性を持つ取引可能な資産を見つけることは非常に難しいです。株価はほとんどは幾何ブラウン運動と同じような動きをするため、平均回帰する戦略は相対的に機能しにくいです。
しかし、例えばペアトレーディングのように、資産を組み合わせることによって、平均回帰性を見つけることは可能です。
最も単純なのは、ペアトレーディングですが、それは、同一の法定通貨を基軸とした資産をロングショートするというものです。
感覚的には、同じセクターの二つの企業同士は同じようなマーケットファクターで、同じようにビジネスに影響する為、似た動きになります。
特定のイベントで相対価格は大きく動くこともありますが、長い目で見て平均回帰する可能性が高いです。(ただし、倒産等極端なイベントはもちろん別です(笑))
ここでは、二つの株を例に見ていきます。エネルギーセクターのApproach Resources Inc(以下AREX)とWhiting Petroleum Corp(以下WLL)を見ていきましょう。と言いたい所ですが、AREXがまさかの倒産しておりました(笑)
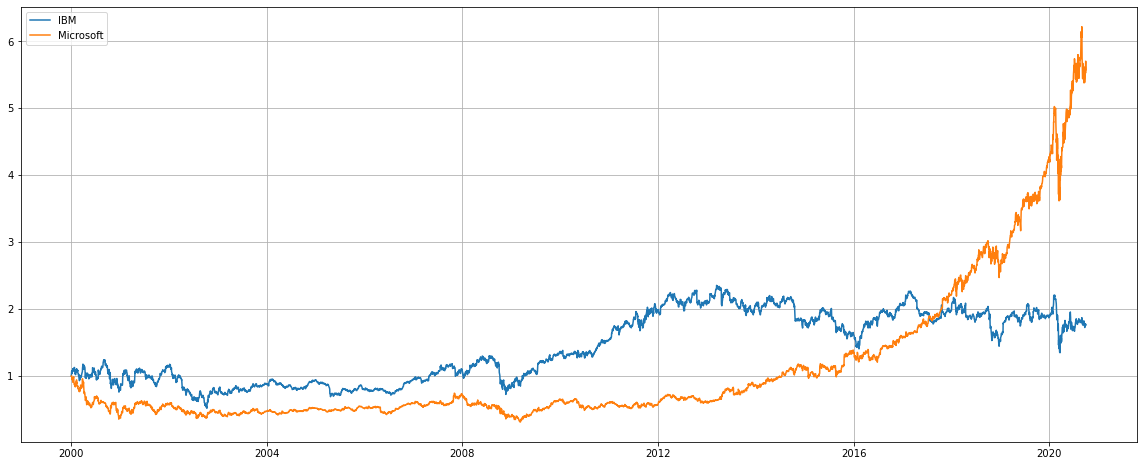
普通に、IBMとMicrosoftについて見ていきましょう(笑)
期間は2000年1月1日から2020年10月4日までで、基準点を2000年1月1日の株価で1としております。
ペアトレーディングのモデルは以下のようにモデリングします。
y(t) = \beta x(t) + \epsilon(t)
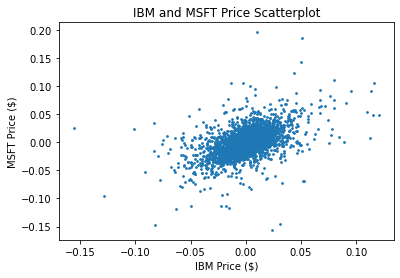
ここで、お互いの価格変化率の散布図を見てみましょう。ピアソンの相関係数は0.5133です。
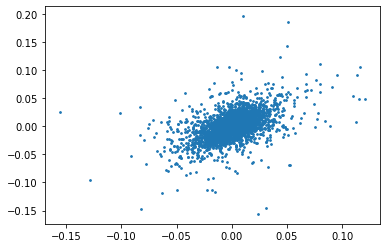
大分同じ動きをしていることが分かりますね。
共和分ADF検定
これは要するに、二つの資産があって、それの差分に対して、ADF検定をするだけです。
コードは以下の通りになります。(原文が古いこともあって大分書き換えてあります。)
インポート
from datetime import datetime
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import pandas as pd
from pandas_datareader import DataReader
import pprint
import statsmodels.tsa.stattools as ts
from sklearn.linear_model import LinearRegression
メソッド定義
def plot_price_series(df, ts1, ts2):
months = mdates.MonthLocator()
fig, ax = plt.subplots(figsize=(20, 8))
ax.plot(df.index, df[ts1], label=ts1)
ax.plot(df.index, df[ts2], label=ts2)
ax.grid(True)
plt.xlabel("Month/Year")
plt.ylabel("Price ($)")
plt.title("%s and %s Daily Prices" % (ts1, ts2))
plt.legend()
plt.show()
def plot_scatter_series(df, ts1, ts2):
plt.xlabel("%s Price ($)" % ts1)
plt.ylabel("%s Price ($)" % ts2)
plt.title("%s and %s Price Scatterplot" % (ts1, ts2))
plt.scatter(df[ts1], df[ts2], s=3)
plt.show()
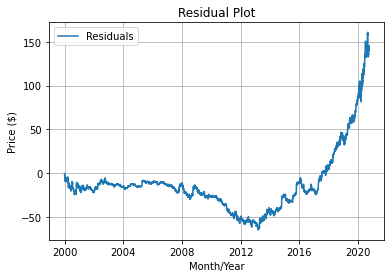
def plot_residuals(df):
months = mdates.MonthLocator()
fig, ax = plt.subplots()
ax.plot(df.index, df["res"], label="Residuals")
ax.grid(True)
plt.xlabel("Month/Year")
plt.ylabel("Price ($)")
plt.title("Residual Plot")
plt.legend()
plt.show()
共和分ADF検定実装
symbol_1 = "IBM"
symbol_2 = "MSFT"
ts1 = DataReader(symbol_1, "yahoo", datetime(2000, 1, 1), datetime(2020, 10, 4))
ts2 = DataReader(symbol_2, "yahoo", datetime(2000, 1, 1), datetime(2020, 10, 4))
df = pd.DataFrame(index=ts1.index)
df[symbol_1] = ts1["Adj Close"]
df[symbol_2] = ts2["Adj Close"]
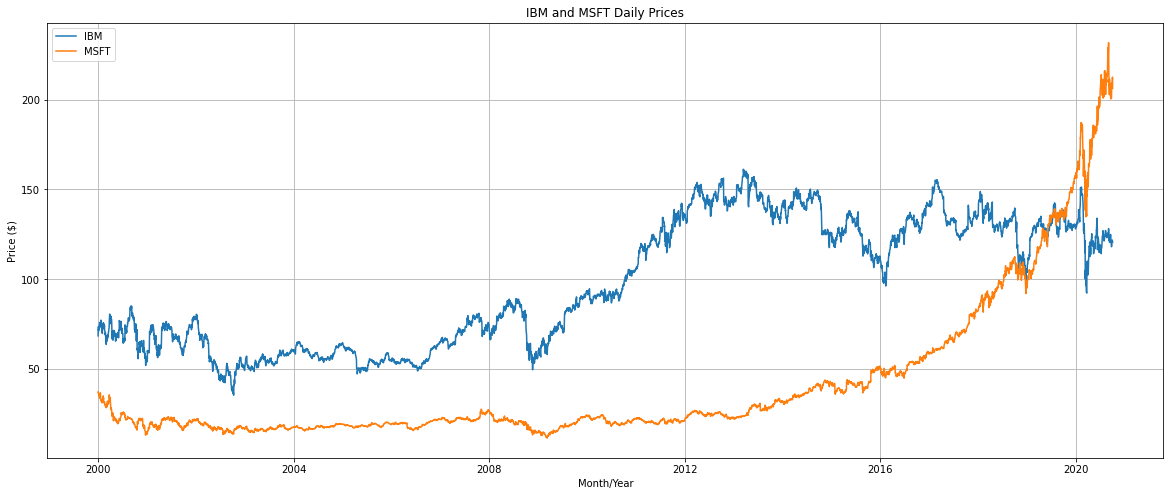
plot_price_series(df, symbol_1, symbol_2)
plot_scatter_series(df.pct_change(), symbol_1, symbol_2)
lr = LinearRegression().fit(df[symbol_1].values.reshape(-1, 1), df[symbol_2],)
beta_hr = lr.coef_[0]
df["res"] = df[symbol_2] - beta_hr * df[symbol_1]
df.dropna(inplace=True)
plot_residuals(df)
cadf = ts.adfuller(df["res"])
pprint.pprint(cadf)
結果
(4.942027424891391,
1.0,
33,
5189,
{'1%': -3.431610847537117,
'10%': -2.567066577632963,
'5%': -2.862097162737307},
15579.126832712373)
統計的に有意ではないため、こちらのペアは平均回帰性を持ちません。ただし、これは長い期間に限った話ですので、1か月等の比較的短期的な期間においては、平均回帰性を示す可能性はあります。
そちらの調査方法は、30日価格変化率を見て、それに対してローリングしながら単回帰して傾き($\beta$)を求める必要があります。
参考文献
- SUCCESSFUL ALGORITHMIC TRADING, Michael L. Halls-Moore
感想
今回の読書感想文は、共和分検定を行うための方法論についてお話しました。
実運用上では、回帰するとき等は将来情報を含まないように注意する必要があります。
また、対象資産が$n$通りあれば$n \choose 2$通りのペアトレーディングの組み合わせが取れる為、回帰性を持つペアを見つけることは比較的容易です。
参考になれば幸いです🙇