文字列辞書のいろんな実装方法

いつもお世話になっております。@kampersandaです。

なんか最終日になって急に空きができたそうなので書こうと思います。急いで書きましたので荒い部分もありますが、書いたことが何より偉いです。おかしい部分や書き残した部分は後々少しずつ修正します。

文字列辞書とは

文字列集合を保存したり検索したりするデータ構造のことを文字列辞書やキーワード辞書、または単に辞書と呼んだりします。連想配列やマップと呼んだりもしますよね。用途に応じてその定義はさまざまですが、身近な例ではC++のstd::map<std::string, int> のようなデータ構造です。

こういうデータ構造を使おうとする時、ありがたいことにプログラミング言語が提供する標準ライブラリで十分だったりします。ですが少しリッチな操作や高速性を要求する場合、適切な技法を選択する必要があります。たとえば集合 {showa, heisei, reiwa} から ei を部分文字列として含む文字列を検索したいとき、std::map でそれを実現するのは難しいですよね。

本記事では、いろいろな文字列辞書の実装技法を知っといて損はない程度に簡単にさらっと紹介します。何らかの目的で文字列辞書を実装しなくてはならなくなった人や、数ある辞書ライブラリのうち何を使ったらいいのかわからない人の参考になれば幸いです。ちなみに、この世にある全ての実装技法を紹介する訳ではないですのでご容赦ください。

定義

まずは本記事で考える文字列辞書を定義します。

$n$ 個の文字列の集合 $S = \{s_1, s_2, \dots, s_n\}$ を保存し、各 $s_i$ にユニークな整数値（id）を割り当てるデータ構造を文字列辞書と呼びます。割り当てる id に厳密な規則はなく、辞書式順に１から割り当てたり、辞書に登録される順に任意のものを割り当てたり、それは実装技法によるものとします。とりあえず $s_i$ にユニークな値を割り当てられることが大切であり、これが実現できれば整数に限らず任意の型の値を $s_i$ に連想づけることができるはずです。

文字列辞書が提供する操作としては、クエリ文字列 $q$ について以下のものを考えます。

• 検索
  • Search：$q \in S$ なら、その id を返す。
  • PrefixSearch：$q$ を接頭辞として含む全ての文字列 $s_i$ の集合を返す。
  • SubstrSearch：$q$ を部分文字列として含む全ての文字列 $s_i$ の集合を返す。
• 更新
  • Insert：$S$ に $q$ を追加し新しい id を割り当てる。
  • Delete：$S$ から $q$ を削除する。

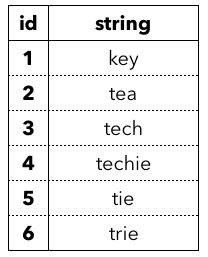
例えば、$S$ を {key, tea, tech, techie, tie, trie} として辞書式順に１から id が割り振られてるとすると、Search(tea) = 2 です。また、PrefixSearch(te) = {tea, tech, techie}、SubstrSearch(ie) = {techie, tie, trie} です。

どの操作を提供するかは実装技法によりますが、少なくとも Search は提供するものを考えます。Insert と Delete を提供しない辞書を更新不可能な辞書と呼び、こうした辞書は $S$ から一度構築されるとそれ以降は内容が更新されないものとします。

技法まとめ

忙しい人のために、これから紹介する技法を表でまとめておきます。$k$ はクエリ文字列の長さです。

技法	Search	Insert	Delete	PrefixSearch	SubstrSearch
整列済み配列	$O(k \log n)$	–	–	✔︎	–
連結リスト	$O(kn)$	$O(k)$	$O(kn)$	–	–
二分探索木	$O(k \log n)$	$O(k \log n)$	$O(k \log n)$	✔︎	–
ハッシュ表	$O(k)$	$O(k)$	$O(k)$	–	–
Trie	$O(k)$	$O(k)$	$O(k)$	✔︎	–
Front-Coding	$O(k \log n)$	–	–	✔︎	–
接尾辞配列	$O(k \log n)$	–	–	✔︎	✔︎

これらはこれから紹介するようにシンプルに実装した場合の性能であり、あくまで目安としてお考えください。今回はメモリ効率などを意識した高度な実装については複雑になるので議論しません。あくまでどのように辞書が実現できるのかに焦点を当てます。

以降の説明では、ハッシュ表の辺りまではすでに教科書などで学んでいる前提で話しますのでご容赦ください。

方法１：整列済み配列

辞書を実装する上で最も単純な技法は、辞書式順に整列された文字列の配列を用いる方法です。例えば、$S=$ {key, tea, tech, techie, tie, trie} に対する整列済み配列は以下のようになります（以降の例でも接尾辞配列を除きこの文字列集合を使います）。

これは $n$ 個の各 $s_i$ へのポインタの配列で実装でき、配列のインデックスがそのまま id になります。C++では以下のようなコンテナで実装できます。

using SortedArray = std::vector<std::string>;

長さ $k$ の文字列に対する Search は、辞書式順に並んでますので配列に対する二分探索で実現できます。その検索時間は $O(k \log n)$ 時間です。PrefixSearch は同じように二分探索し $q$ が接頭辞として含まれる $s_i$ をひとつ見つけると、辞書式順に並んでるおかげで残りの解は $s_i$ と隣り合っているはずなので、$s_i$ の周りを線形に探索することで実現できます。SubstrSearch は難しそうです。

一方で配列は整列されていなければなりませんので、Insert や Delete は配列を作り直す必要があります。ここでは更新不可能とします。

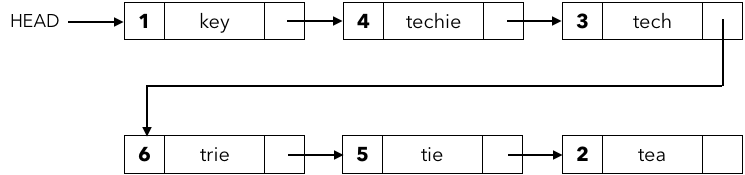
方法２：連結リスト

id と文字列のペアを要素とする連結リストを以下のように組むことで、簡単に更新可能な辞書を実現することができます。

C++では以下のようなコンテナで実装できます。

struct LinkedList {
    int id;
    std::string str;
    LinkedList* next;
};

Insert は連結リストの先頭に文字列を挿入することで $O(k)$ 時間で実現できます。ただし、Search は連結リストの先頭からひとつひとつチェックしていく必要があるので $O(kn)$ 時間とかなり遅いです。Delete も一度検索する必要があるので $O(kn)$ 時間です。

また PrefixSearch のような操作も、文字列が整列されていないので効率的に実現するのは難しそうです。¹

方法３：二分探索木

整列済み配列ではSearchが $O(k \log n)$ 時間の代わりに更新が不可能でした。一方で連結リストは $O(k)$ 時間で Insert できる代わりに Search と Delete が $O(kn)$ 時間も必要でした。我々はこの一得一失を受け入れなくてはならないのでしょうか。もちろんそんなことなくて二分探索木を使いましょう。

二分探索木はバランスされているとき、Search も Insert も Delete も $O(k \log n)$ 時間で実現できます。PrefixSearch も二分探索木内で $s_i$ が辞書式順が保持されているため、探索する部分木を絞り込みながら実現できそうです。

赤黒木などを使えば更新後も二分探索木のバランスを保持することができます。実際、C++の標準ライブラリでは赤黒木で二分探索木を実装しており、以下のようなコンテナを使うことで実装できます。

using BinaryTree = std::map<std::string, int>;

赤黒木については解説しませんが、その本質を知りたい人は16日目の記事を読みましょう。

方法４：ハッシュ表

$n$ が小さい場合は二分探索木で十分高速な文字列辞書が実現できるでしょう。ただ $n$ が大きい場合は $O(\log n)$ 時間がうれしくないので、そういう時はハッシュ表を使いましょう。

ハッシュ表にはいくつか種類がありますが、上の図はチェイン法によるハッシュ表を示しています。チェイン法では、ハッシュ関数を用いて文字列をハッシュ表上のあるインデックスに写像し、衝突を連結リストにより解決します。

ハッシュ表を使えば、Search も Insert も Delete も $O(k)$ 時間で実現できます。$s_i$ をランダムに分散させますので、PrefixSearch などのリッチな操作を実現するのは不可能ですが、こうした操作が必要でない場合は、非常に強力な技法です。

ハッシュ表による文字列辞書は、C++の標準ライブラリを使えば簡単に実装できます。

using HashTable = std::unordered_map<std::string, int>;

ここまでは文字列辞書というよりは汎用的なコンテナの要素を文字列にしただけのものでした。だから非効率だというわけではないですが、文字列に特化した技法を用いることでもっと高性能な辞書を実装することができます。以降ではそんな技法を紹介します。

方法５：Trie

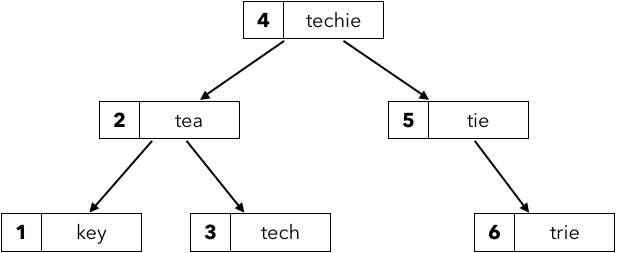
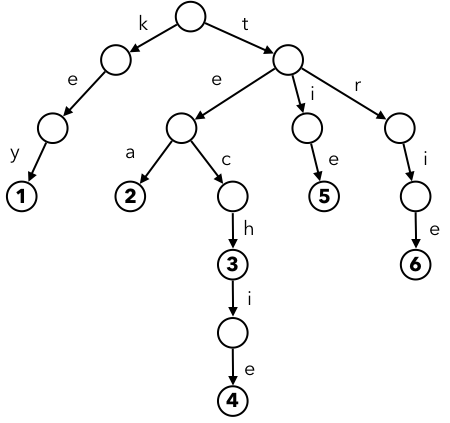
Trieは枝に文字が付随した木構造で、文字列辞書を実現するために広く使われるのデータ構造です。$s_1, s_2, \dots, s_n$ の接頭辞を併合することで、文字を使って子に遷移できるような木構造を構築します。根からある節点まで経路が $s_i$ に対応します。以下の図を見てもらう方が早いですね。

このTrieを使って文字列 tea を検索する場合、根から t、e、a と一文字づつ遷移し、最終的に②の節点にたどり着きます。いずれかの節点が $s_i$ に対応するはずなので、対応する節点にその id を付随しておくことで文字列辞書を実現できす。

このTrieはどうすれば実装できるでしょうか。Trieの実装に関する研究は古くからよくされており、非常に多くの技法が存在しますが、少なくとも各節点が文字によって子を特定することができれば実装できます。すなわち、各節点を文字から子への写像を与える辞書によって実装すればよさそうです。時間計算量的にハッシュ表を使うのがよさそうですね。C++では以下のようなコンテナで実装できます。

struct TrieNode {
    std::unordered_map<char, TrieNode*> children;
    int id;
};

ハッシュ表を使うことによって、子を $O(1)$ 時間で特定できます。すなわち、$O(k)$ 時間で Search が実行できます。Insert も Delete も一度検索し、対応する節点を追加したり削除したりすることで $O(k)$ 時間で実行できます。

さらに Trie は文字列の接頭辞を併合しているため、接頭辞を使った検索との相性もいいです。$q$ で検索し、辿り着いた節点を根とする部分木を走査することで PrefixSearch は実行できます。

方法６：Front-Coding

Front-Coding は整列済み配列を圧縮して保持する技法で、自然言語やURLの接頭辞がよく似ている特徴を利用して圧縮します。Front-Coding は整列済みの文字列に対する圧縮法ですので、ここでは辞書の更新は考えません。

Front-Codingでは整列済み配列の各文字列を（１）その直前の文字列との最長共通接頭辞長と（２）残った接尾辞のペアに符号化します。例えば、以下の例の techie は直前の tech と比較し、その最長共通接頭辞長４と残りの接尾辞 ie のペアに符号化されます。以降、この符号を (lcp, suffix) と表記します。

符号 (lcp, suffix) から元の文字列を復元する場合は、直前の文字列の長さ lcp の接頭辞と suffix を結合することで復元できます。ただし直前の文字列も符号化されてるとすると結局先頭から全て復元しないといけないことになり、Search は $O(nk)$ 時間となってしまいます。

そこで Front-Coding を辞書として使うために、整列済み配列を $b$ 個ごとのブロックに分割し、その各ブロックの先頭のみを符号化せずにそのまま保持しておきます。$i$ 番目の文字列を復元するときには、そのブロックのみを先頭から復元するだけで済みます。例えば、以下の例では $b=4$ 個ごとのブロックに分割し、５番目の tie# がブロックの先頭として符号化されずにそのまま保存されます。

この Front-Coding 辞書の Search は（１）ブロックの先頭文字列に対する二分探索、と（２）該当ブロックの先頭から復元しつつ探索、の２段階で実現できます。例えば Trie を検索する場合、各ブロックの先頭 key と tie に対する二分探索で trie が含まれているかもしれない２番目のブロックを特定し、tie から復元しつつ探索することで６番目に trie が存在することを発見できます。

その時間は、ブロックの数が $n/b$ 個で各ブロックに属する文字列の数が $b$ なので $O(k\log(n/b) + kb)$ 時間です。$b$ を定数と見なせば、$O(k \log n)$ 時間で整列済み配列と同じ検索時間です。PrefixSearch も整列済み配列と同様の方法で実現できます。

Front-Codingの良い点は、$s_i$ の接頭辞がよく似ている場合、多くの接頭辞を整数値に置き換えられ、大幅な辞書の圧縮が期待できます（もちろんその整数値をどう保存するのかによりますけど）。URLとかにすごい強力そうです。

方法７：接尾辞配列

全文索引とはあるテキストが与えられたとき、それに含まれる文字列の位置を高速に報告することができるデータ構造です。全文索引を実現する技法はいくつかありますが、今回は接尾辞配列と呼ばれるデータ構造を考え、接尾辞配列を用いて文字列辞書を実装する方法を紹介します。ここでも辞書の更新は考えず、検索のみを提供する辞書を考えます。ただしリッチです。

接尾辞配列の説明は既存の記事に丸投げします。知らない人は読んできてください。

接尾辞配列を用いた辞書では、文字列集合 $s_1, s_2, ..., s_n$ を特殊文字 # で連結し得られるテキスト $T =$ #$s_1$#$s_2$#$...$#$s_n$# に対し接尾辞配列を構築します。ここで # は $s_i$ には現れないどの文字よりも辞書式順で小さい特殊文字であり、いわゆるNULL文字だと思っていただいて問題ないです。

例えば文字列 tea, tech, techie を連結したテキスト #tea#tech#techie# に対し接尾辞配列を構築した例が以下になります。

$T$ の長さを $N$ とすると、長さ $N$ の接尾辞配列 $SA$ が得られ、この $T$ と $SA$ を用いて検索を行います（図の Suffixes は実際には保持してません）。

その性質として、$T[N] = $# なので、かならず $SA[1] = N$ になり、$SA$ の最初の要素は $T$ の末尾を指し示します。そして、$1 \leq i \leq n$ について、$SA[i+1]$ は接尾辞 #$s_i$#$s_{i+1}$#$...$#$s_n$# を示します。例えば、$SA[1+1]=1$ は $T[1]T[2]...=$#tea#$...$、 $SA[2+1]=5$ は $T[5]T[6]...=$#tech#$...$、$SA[3+1]=10$ は $T[10]T[11]... =$#techie#、というように各 $s_i$ の先頭を指し示しています。すなわち、Search は $SA[2]$ から $SA[n+1]$ の範囲を #$q$# で二分探索することで実現できます。

さて，ここまででは整列済み配列で十分じゃないのかという感じですが，接尾辞配列の利点は PrefixSearch に加え、SubstrSearch が実行できる点です。

まず PrefixSearch は末尾の特殊文字を取り除いた #$q$ で $SA[2]$ から $SA[n+1]$ の範囲を二分探索することで実現できます。これは、整列済み配列による辞書と同じ要領です。

SubstrSearch は先頭と末尾の特殊文字を取り除いた $q$ で $SA[n+2]$ から $SA[N]$ までの範囲を二分探索することで、$T$ 中の $q$ を部分文字列として含む位置を全文検索できます。これは $SA$ の範囲として得られ、例えば ch を部分文字列として含む位置を示す $SA$ の範囲は $SA[6]$ から $SA[7]$ です。その位置で $T$ にアクセスすることで、$q$ を部分文字列として含む文字列 $s_i$ を得ることができます。$s_i$ は # で囲まれてるはずなので、$T$ から復元するのは簡単ですよね。

今回は接尾辞配列を用いたので Insert や Delete は考えませんでしたが、接尾辞木とか使ったら更新できたりするんでしょうか。知りませんけど。

おすすめなライブラリ

書きたい！！

おわりに

12/25 に間に合わなかったのが悔やまれますが、書いたことが何より偉いです。Trie は図を作るのがめんどくさかったので棚上げしました。また元気が出たら書きます。（書きました）

1. もちろん連結リストを整列させながら作ることもできますが、二分探索できない連結リストでそれをする利点もあまりないので（ないとは言ってない）割愛します。あくまでInsertが簡単にできることが大切です。 ↩