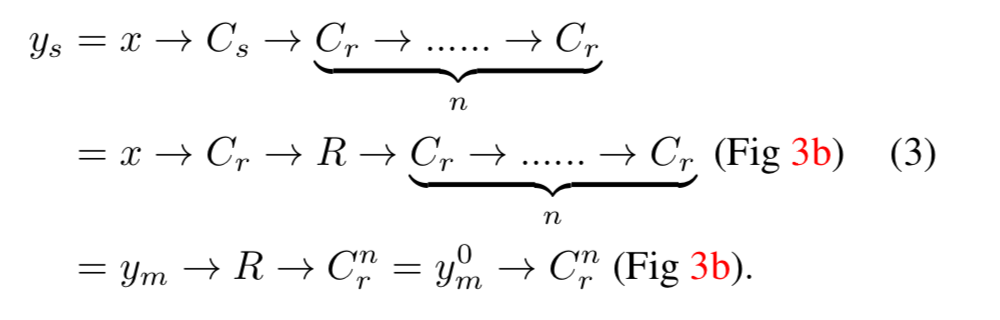DeepLabに代わり現在のSOTAであるFastFCN(JPU)の論文解説

2019/3/28に投稿された、今現在のセグメンテーションのstate-of-the-artです
Joint Pyramid Upsampling (JPU)という手法を用いて、state-of-the-artの精度かつ、DilatedFCNに比べて3倍以上高速なセグメンテーションを可能にした論文です

論文の概要

論文名: FastFCN: Rethinking Dilated Convolution in the Backbone for Semantic
arXiv: https://arxiv.org/abs/1903.11816
Github: https://github.com/wuhuikai/FastFCN

Abstract

• 最近のセグメンテーションのアプローチでは、高解像度の特徴量マップを得るためにDilated Convolutionをbackbornに使っているが、これは計算コストとメモリ消費が激しい
• これを解決するために、Joint Pyramid Upsampling (JPU)というモジュールを導入します これは高解像度の特徴量マップを得る問題を、Joint Upsampleの問題に置き換えるものです。
• JPUによって、精度を落とすことなく、計算コストを３倍以上減らすことができます
• Dilated ConvolutionをJPUモジュールに置き換えることによって、Pascal Context datasetとADE20K datasetにおいて、３倍以上高速に動作しながら、state-of-the-artのスコアを出しました。

1. Introduction

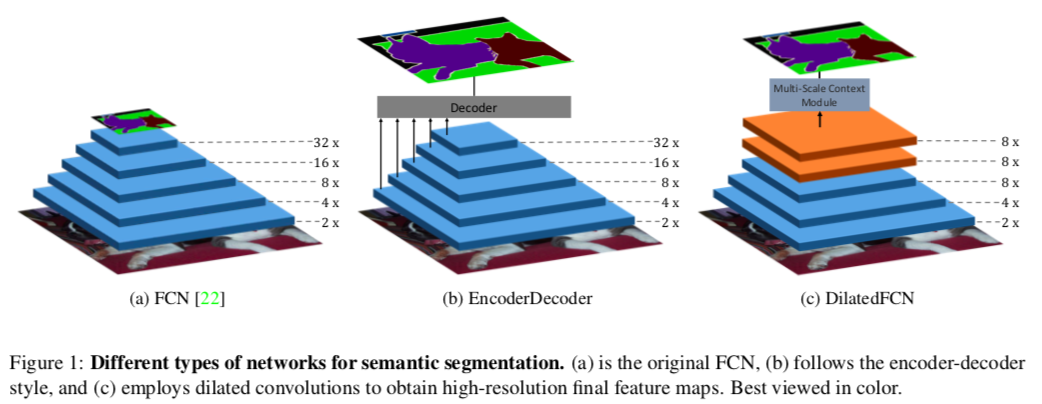
• 最初のFCN(Fully Convolution Network)は、ダウンサンプルによって低解像度の特徴量マップを生み出すため、細かい情報は失われ、境界線付近で間違った予測をすることが多くなります。Fig 1(a)のように、典型的なFCNでは5回ダウンサンプリングをし、特徴量マップは約1/32の解像度になる。

• 高解像度の特徴量マップを得るため、元のFCNをセマンティックな情報を得るためのEncoderとして用いて、DecoderではEncoderの中の特徴量マップを徐々に取り入れていくことで、徐々に空間情報を補填していくEncoderDecoder構造が提案されています（Fig 1(b))

• その後提案されたDeeplabでは、最初のFCNから最後の二つのダウンサンプルを取り除き、代わりにdilated (atrous) convolution を追加して、受容野の大きさが変わらないようにしています。この種の方法はEncoderDecoder構造のモデルを様々なベンチマークで上回っていきました。Fig 1(c)でわかるように、DilatedFCNの最後の特徴量マップは他のものより４倍程度大きく、より多くの空間情報を保持しています。

• dialted convolutionは最後の特徴量マップがより高解像度の空間情報を保持するために重要な役割を果たしていますが、計算コストとメモリ使用量が大きい点が問題になっています。

• この問題を解決するためにJoint Pyramid Upsampling (JPU)を導入します。最初のFCNをbackbornとして用いて、その各層から得られる特徴量マップをJPUに通すことで、最終的にOutput Strideが8（入力画像の1/8の解像度）の高解像度の特徴量マップが得ることができます。さらに、DilatedFCNに比べて精度を落とさないまま、計算コストとメモリ使用量も大幅に減らすことができます。

• 実験をすると、3倍早く動きながらstate-of-the-artの精度を出すことができた

  • Pascal Context datasetでは53.13%(mIoU)でSOTA
  • ADE20K datasetでは42.75%(mIoU)でSOTA

2. Related Work

2.1. Semantic Segmentation

EncoderDecoderとDilatedFCNについてIntroductionとほぼ同じことを説明してるだけなので割愛

2.2. Upsampling

低解像度の特徴量マップをupsampleして高解像度のものを取り出す必要があります

Joint Upsampling

この内容は3.3.1 Backgroundの方で詳しく説明するのでここでは割愛

Data-Dependent Upsampling

ラベル空間の冗長性を利用して低解像度の特徴量マップからpixel-wiseの予測をするDUpsamplingもこの論文の方法と関連していますが、DUpsamplingはラベル空間に大きく依存しており、複雑なラベルには対応できなくなる点がこの論文の優位性

3. Method

3.1. DilatedFCN

これもほぼIntroductionと同じ内容なので割愛。内容がないよう〜
DeepLabではFig 1(c)にあるように最後の２層はDilated Convolutionにして計算量を変えずに受容野を広げますよっていうお話

ちょっとだけ参考として、dilated(atrous) Convolutionというのはこんな感じです。gif画像はDilation rate(畳み込みをする間隔）が2の場合で、1の場合は普通の畳み込みと同じになります。

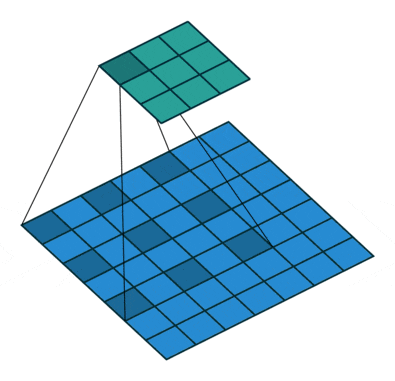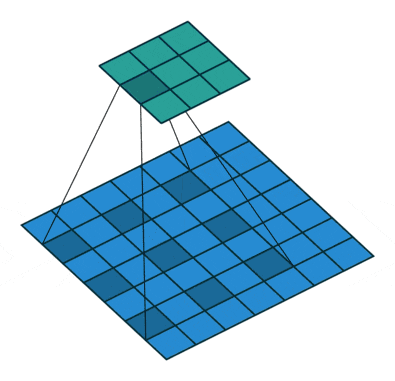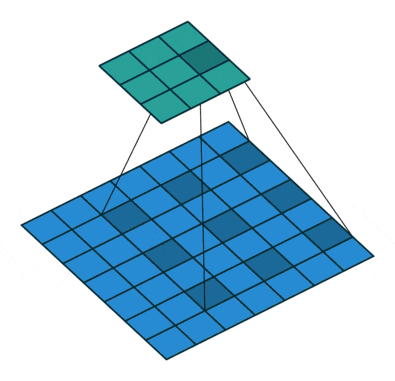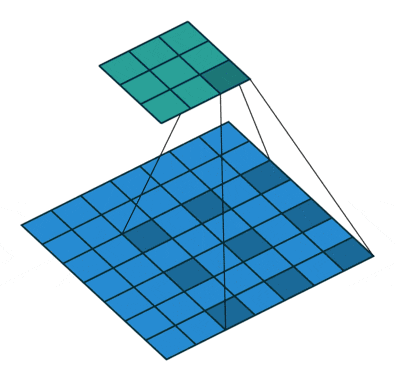
3.2. The Framework of Our Method

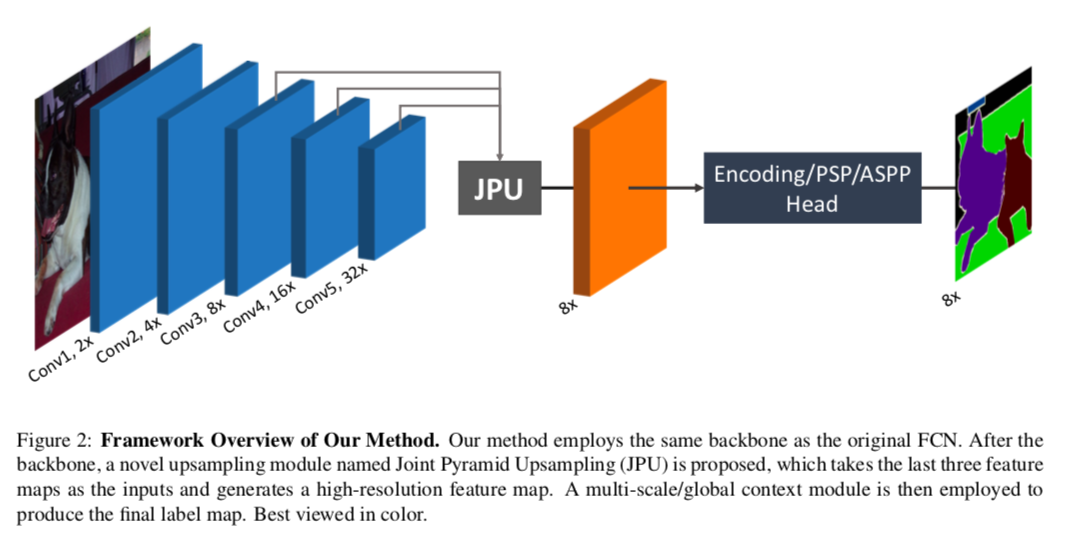
この論文では、計算コストとメモリ使用量を抑えつつ、DilatedFCNの最終層の特徴量マップを近似することが目的

1. そのためにまず、Dilated FCNで無くした最後二つの普通のConvolutionを元に戻します。これによって、Fig 2にあるようにbackbornは元のFCNと同じものになります
2. そして、Dilated FCNと似た特徴量マップを得るため、最後の３つの層の特徴量マップをインプットとするJoint Pyramid Upsampling (JPU)を導入します。
3. そのあとmulti-scale context module（PSPもしくはASPP）かglobal context module(Encoding)に通して、最終的な予測値を出します。

backbornにResnet101を使った場合、Dilated Convolutionに比べて、residual blockが23個の場合は1/4の計算コスト&メモリ使用量、3個の場合は1/16になります

3.3. Joint Pyramid Upsampling

Dilated FCNと同じ特徴量マップを作り出すのは、Joint Upsampleの問題として考えることができる

3.3.1 Background

Joint Upsampling

低解像度のguidance画像$x_l$から、低解像度のtarget画像$y_l$が、

y_l = f(x_l)

という変換で得られるとします。これから考える問題は、この$f(\cdot)$を近似する、$\hat{f}(\cdot)$を求めることです。
一般的に、$\hat{f}(\cdot)$は$f(\cdot)$よりも計算コストが小さくなります。例えば、$f(\cdot)$がもし多層パーセプトロンで形成されたものなら、$\hat{f}(\cdot)$は簡単な線形演算子の形で求められます。
この$\hat{f}(\cdot)$を用いることで、高解像度のguidance画像$x_h$が与えられた時は、

y_h = \hat{f}(x_h)

として、少ない計算量で高解像度のtarget画像を得ることができます。

問題を定式化すると、

y_h = \hat{f}(x_h), \mathrm{where}~ \hat{f}(\cdot) = \mathrm{argmin}_{h(\cdot)\in \bf{H}} \| y_l - h(xl) \| 

ここで$\bf{H}$は考えられる変換、$||\cdot||$は距離関数です

Dilated Convolution

Dilated Convolutionは、Deeplabで提案された、受容野の大きさを変えずに高解像度の特徴量マップを取り出す方法ですが、これは次のように考えることができます。
Fig 3(a)は、一次元でdilation rateが2の場合を示していますが、この操作は以下の３つの操作に分解できます

1. Split : inputの$f_{in}$を、$f_{in}^0$と$f_{in}^1$の二つのグループにわける
2. Conv : それぞれに同じ畳み込みを施し、$f_{out}^0$と$f_{out}^1$を得る
3. Merge : $f_{out}^0$と$f_{out}^1$を互い違いになるように統合して、$f_{out}$を得る

ここでは簡単のために一次元で考えていますが、２次元でも同様の分解ができます。

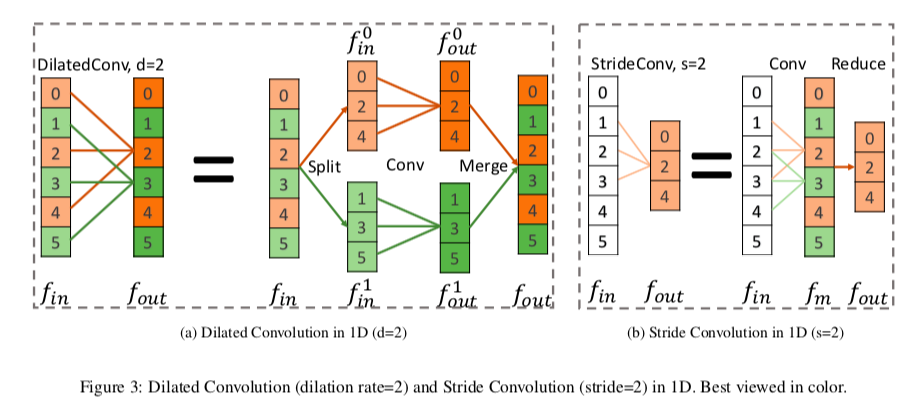
Stride Convolution

Stride Convolutionは、inputの特徴量を、解像度を減らしてoutputの特徴量に変換する方法です。
Fig 3(b)で一次元の場合を示していますが、これも二段階の操作に分解できます

1. Conv : $f_{in}$に普通の畳み込みをして、中間の特徴量$f_m$を取り出す
2. Reduce : $f_m$の奇数番目を取り除いて、$f_{out}$を得る

これも２次元の場合でも同様のことが成り立ちます。

3.3.2 Reformulating into Joint Upsampling

DilatedFCNと、提案手法の違いを見ていきます。
例として、backbornのConv4の特徴量マップ（Fig 2のConv4の出力）をinputとして、そこからoutputの特徴量マップを作る方法で比較します。

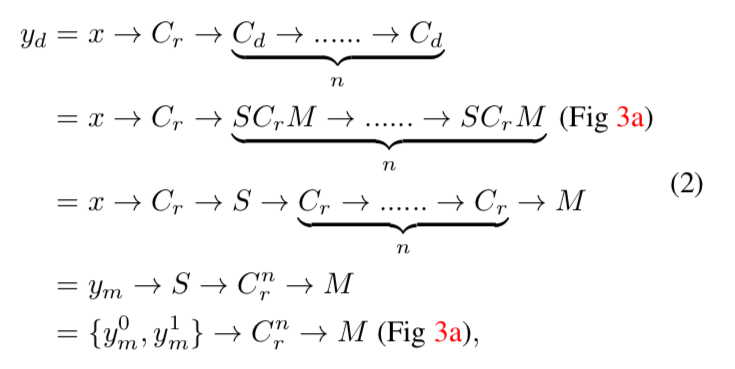
まず、DilatedFCNでは、まず最初にinputの特徴量マップ$x$に普通の畳み込みをしたあと、dilated畳み込みを何度か行なって、outputの特徴量マップ$y_d$を作ります。
これは以下のように定式化できます。

• [記号の説明]
  • $C_r$ : 普通の(regular)畳み込み（$C_r^n$は$C_r$が$n$層あることを示す）
  • $C_d$ : dilated畳み込み
  • $C_s$ : stride畳み込み
  • $S$ : 上で説明したSplitの操作
  • $M$ : 上で説明したMergeの操作
  • $R$ : 上で説明したReduceの操作
  • $\rightarrow$ は操作を施すことを意味します

一行目と二行目の式変形は、先ほど説明したようにdilated畳み込みの分解で、三行目に行くときに、$S$と$M$の操作は相殺されます。
四行目の$y_m$は、$x$に$C_r$を施したものです。
五行目の$y_m^0$と$y_m^1$は、$y_m$を偶数番目と奇数番目で分解したものです

　一方、提案手法ではoutput特徴量マップ$y_s$は以下のようにして得られます。

以上より、$y_d$と$y_s$は、同じ$C_r^n$を$y_m$と$y_m^0$のどちらに施すかという点だけがことなり、$y_m^0$は$y_m$のダウンサンプリングとなっています。
そのため、$x$と$y_s$が与えられたとき、$y_d$を近似する$y$は、以下のようにして求めることができます。

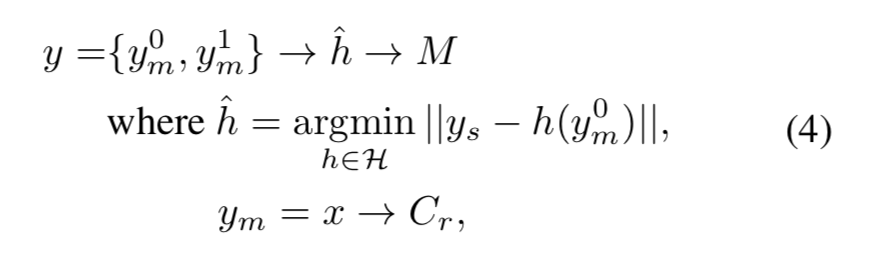
これは先ほど定式化したJoint Upsamplingの問題そのものです。
Conv5をインプットとした場合にも同じ結果が得られます。
これから、この$\hat{h}$を表現する方法を考えていきます。

3.3.3 Solving with CNNs

$\hat{h}$をCNNで表現する方法を考えます。
必要な要素としては、

• $x$に$C_r$を施して、$y_m$を作る
• そして、$y_m^0$からの特徴量マップと、$y_s$を一つに集める

ことが挙げられます。

そのために、以下のようにJPU moduleを定義しました。

具体的には、

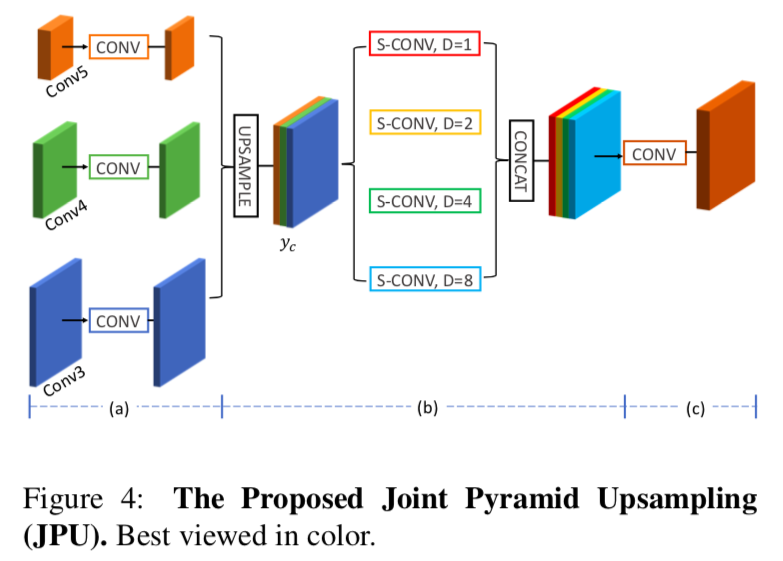
1. まず、Fig 4(a)の部分で、inputの特徴量マップに普通の畳み込みをします。これは$y_m$を作り出すことに対応してます
2. 得られたそれぞれの特徴量マップの次元を減らします。これにより計算コストを抑えることができます。
3. 特徴量マップをupsampleして、cancatして$y_c$をつくります。
4. Fig 4(b)の部分で、$y_c$に、dilation rateが$1,2,4,8$のdilated畳み込みを並行して行います。

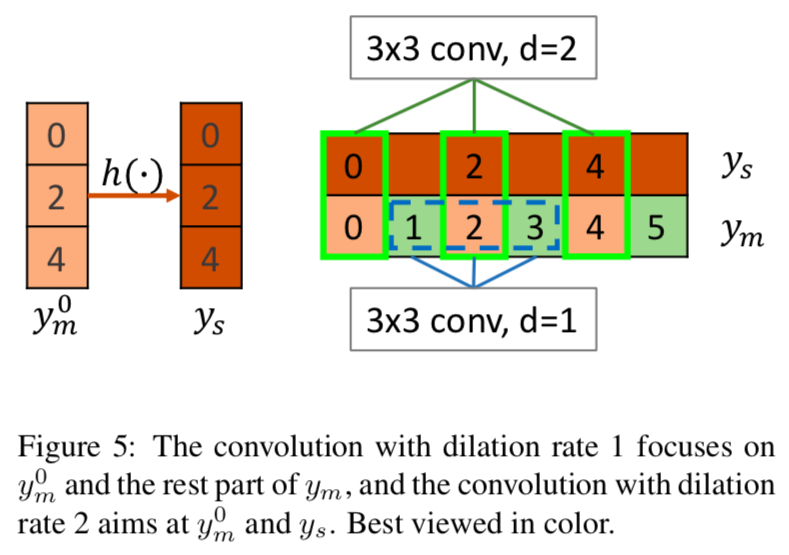
dilation rate=1の操作は、Fig 5の青で囲んだ部分をたたみ込んでいるので、$y_m^0$と$y_m$のそれ以外の部分との関係性を得る働きをします。
dilation rateが2, 4, 8の操作は、Fig 5の緑で囲んだ部分（の一部）をたたみ込むことになるので、求めたい$y_m^0$から$y_s$への写像$\hat{h}(\cdot)$を形成する働きを持ちます。

このようにして、JPUはマルチスケールの特徴量を、マルチレベルで取り込むことが可能です。これは最終層の特徴量しか考慮しないASPP moduleとの大きな違いです。

そして最後に、$y_m^0$と$y_m$のそれ以外の部分をつなぐために、Fig 4(c)の部分でもう一度普通の畳み込みを行います。これの出力が最終的な予測値となります。

4. Experiment

4.1. Experimental Settings

Dataset

Pascal Context datasetの60ラベルを使いましたという話

Implementation Details

• PyTorchで実装
• 前処理はrandom scaleとrandom fliplr
• そのあと480×480にクロップして、batchsize=16で学習
• optimizerはSGDでmomentum=0.9, weight_decay=1e-4、80epoch学習
• 学習率は最初0.001から徐々に減らしていく
• loss funcは、pixel-wise cross-entropy lossを使う
• ResNet-50とResNet-101をbackbornとして使う

ここからは実験の結果だけを簡単に示していきます

Table 1

Headにつかうモジュールと、output stride(OS)を変えたときに精度はどうなるか
JPUが最も良い結果となっている

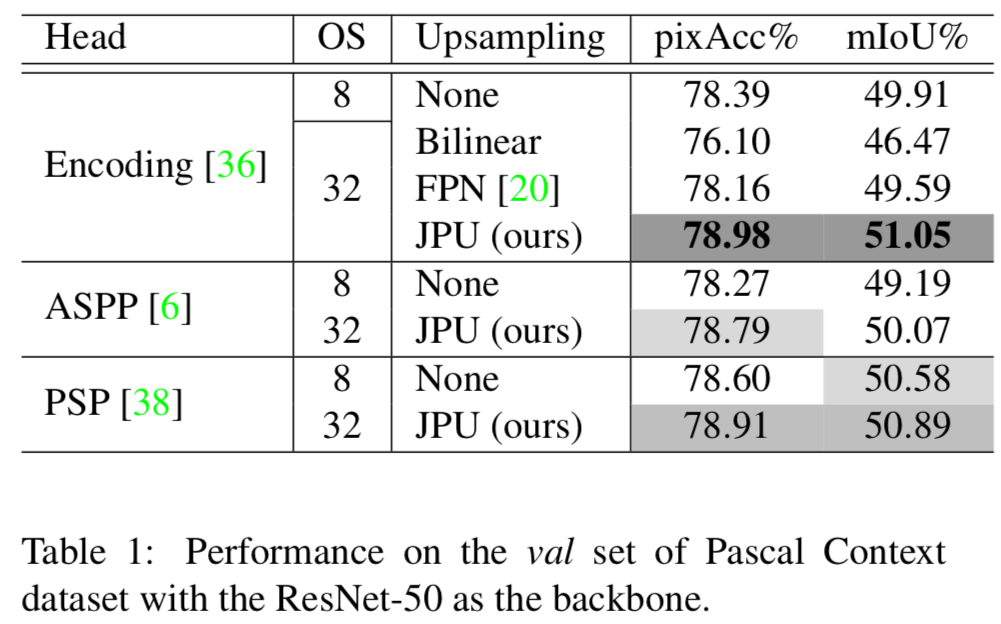
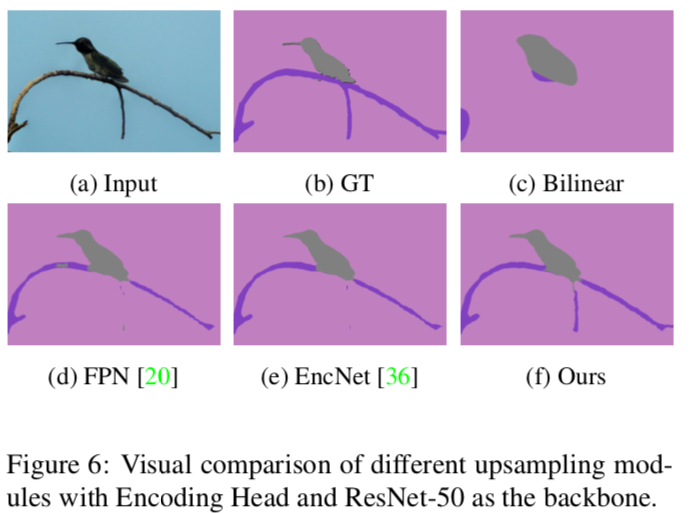
Figure 6

様々なUpsamplingのモジュールを使った場合の予測値

Table 2

計算時間がどれくらいかかるか(FPS)を調べたもの
実行速度はFPNと同じくらいだが、JPUの方が精度は優っている

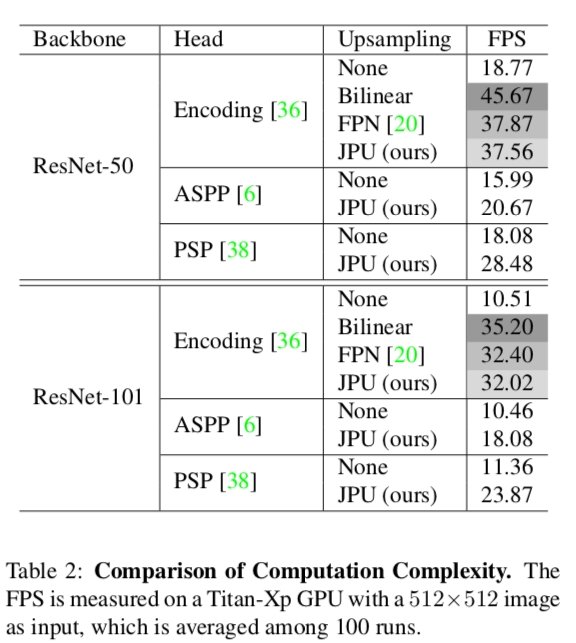
Table 3

Pascal Context dataset(val)で、歴代のSOTA手法に比べたJPUの精度
State of the art‼️

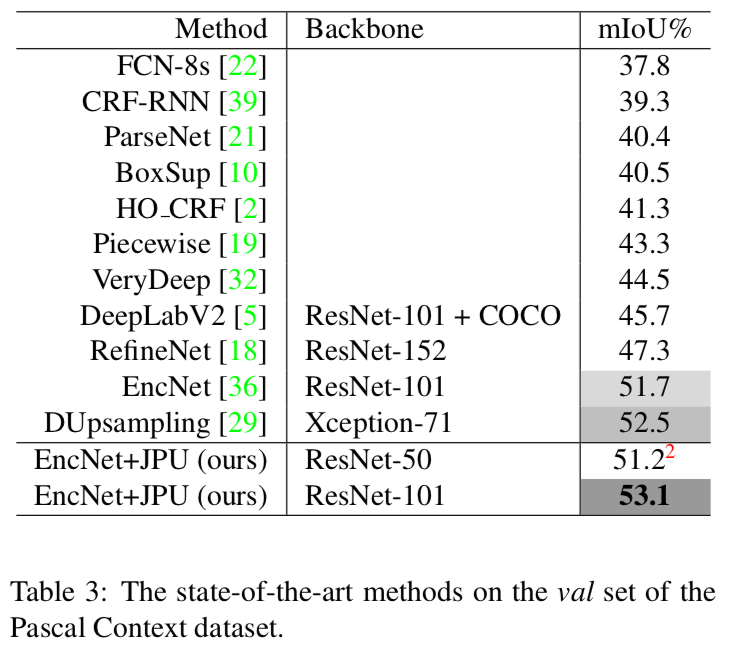
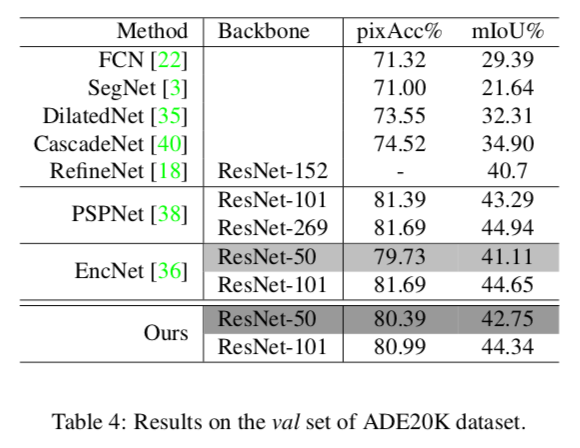
Table 4

ADE20K(val)での精度
これもJPUが一番

Table 5

ADE20K(test)での精度
これもJPUが一番
上の二つはCOCO-Place challenge 2017の一位と二位

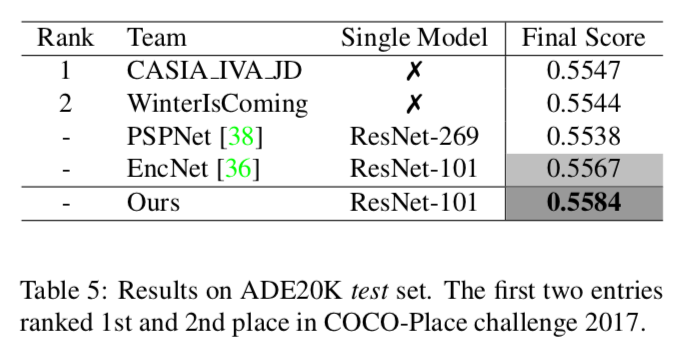
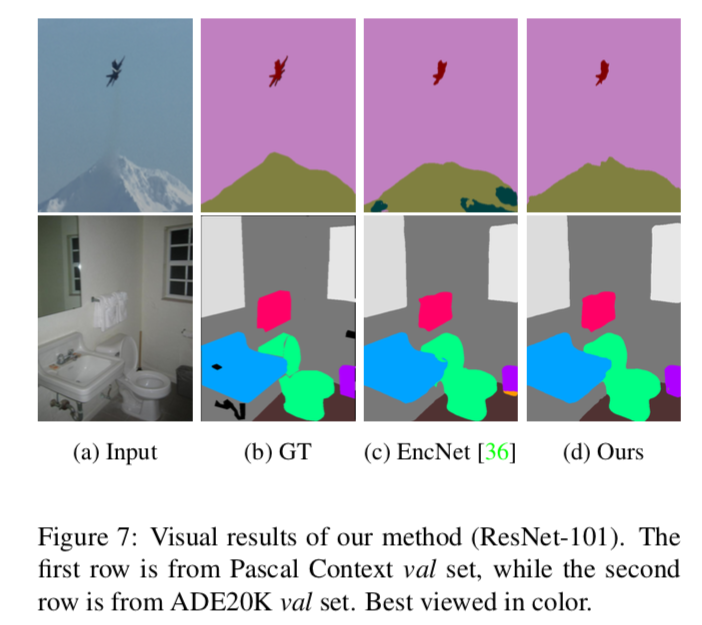
Figure 7

視覚的な結果

5. Conclusion

• dilated convolutionとstride convolutionの違いを解析し、その解析を元に、高解像度の特徴量マップを生成するJPU moduleを提案した。
• dilated convolutionをJPUに変更することにより、精度はそのままで計算コストを３倍以上抑えることができた。
• 実験の結果、JPUは他のupsampleモジュールよりも高精度であることがわかった
• 二つのセグメンテーションのデータセットで、JPUはstate-of-the-artの成績を収めることができた