E-Cell4の簡単な使い方 中級編

準備

インストールについては別記事にありますのでそちらを参考にして下さい.

• Windows 7かMac OS X上でE-Cell4を使ってみる

本記事は中級編です. 初級編を理解していることを前提とします.

• E-Cell4の簡単な使い方 初級編

また本記事ではIPython Notebookの利用を前提とする部分があります.

使い方

E-Cell4における空間

初級編ではE-Cell4における3つの要素Model, World, Simulatorについて説明した. また, 常微分方程式ソルバであるodeと確率論的手法であるgillespieを用いて簡単な計算を試した.

odeやgillespieで計算を行なう際に大きさを与えてWorldを作成したがE-Cell4における空間の取り扱いはどのようなものだろうか?

from ecell4 import *

w1 = ode.ODEWorld(Real3(1, 1, 1))
w2 = gillespie.GillespieWorld(Real3(1, 1, 1))

odeとgillespieでは上の例のように一辺が1の立方体の中で計算を行ったが実際にはその容積しか問題ではない. つまり,

w3 = ode.ODEWorld(Real3(2, 0.5, 1))  # is almost equivalent to 'w1'
w4 = gillespie.GillespieWorld(Real3(2, 2, 0.25))  # is almost equivalent to 'w2'

としても結局容積として1を与えるので同じ計算結果を示すだろう.

これは実際試験管内のように十分に攪拌され, 空間的に均一な系では妥当に思える. しかしながら, 細胞内は明かに空間的に一様とは言えない. こうした分子の局在を考慮するためには空間を考慮した生化学計算が必要である.

E-Cell4では様々な空間表現やそれに対応した計算技法が利用可能である. 以下ではまずその内の1つである空間Gillespie法を例にE-Cell4における空間の取り扱いについて見ていく.

空間Gillespie法

E-Cell4で空間Gillespie法¹は'meso'モジュールに含まれている. まずは何も考えずに初級編で見たように'run_simulation'を用いて計算してみよう.

import numpy
from ecell4 import *

with reaction_rules():
    A + B == C | (0.01, 0.3)

y = run_simulation(numpy.linspace(0, 10, 100), {'C': 60}, solver='meso')

\frac{d\mathrm{C}}{dt}=0.01\frac{\mathrm{A}}{V}\frac{\mathrm{B}}{V}-0.3\frac{\mathrm{C}}{V}=0\\
0.01\left(60-\mathrm{C}\right)^2=0.3\mathrm{C}\times V\\
\mathrm{C}=30

odeやgillespieに比べて幾分時間がかかったかもしれないがほぼ同じ結果が得られるだろう. それもそのはず, mesoモジュールは空間の設定を加えなければgillespieとほとんど等価な計算を行う. では, 'run_simulation'を展開してみよう.

equilibrium3.py

from ecell4 import *

with reaction_rules():
    A + B == C | (0.01, 0.3)

m = get_model()

w = meso.MesoscopicWorld(Real3(1, 1, 1), Integer3(1, 1, 1))  # XXX: Point2
w.bind_to(m)  # XXX: Point1
w.add_molecules(Species('C'), 60)

sim = meso.MesoscopicSimulator(w)  # XXX: Point1
obs = FixedIntervalNumberObserver(0.1, ('A', 'B', 'C'))
sim.run(10, obs)

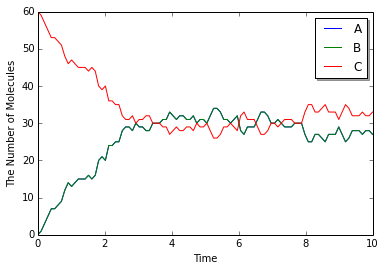
viz.plot_number_observer(obs)

使うものがMesoscopicWorld, MesoscopicSimulatorになった以外はほとんど同じであるが, いくつか新しい要素が出てきたので見ていこう.

まず, 'w.bind_to(m)'ではWorldにModelを関連付けている. 初級編ではこれをせずに済ませたが, 空間的技法ではSpeciesの属性が非常に重要となるので忘れないようにしよう. その代わりにMesoscopicSimulatorにはWorldだけを与えれば十分である.

次に重要な違いとしてMesoscopicWorldを作る際に, 2つ目の引数として'Integer3(1, 1, 1)'を与えている
². これはODEWorldやGillespieWorldではみられなかったものだ. これが何かを説明する前にとりあえず変更してどうなるか試してみる.

w = meso.MesoscopicWorld(Real3(1, 1, 1), Integer3(4, 4, 4))  # <- Integer3(1, 1, 1)

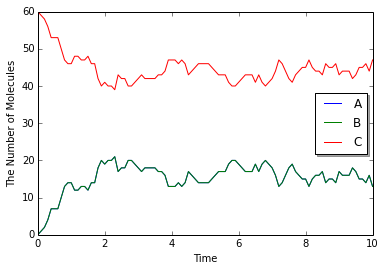
先程とは様子の違う結果が得られたものと思う. 数字をより大きくすれば結果の違いもより顕著になるだろう.

実はこの2つ目の引数は空間の分割数を表している. mesoはgillespieとほぼ同じであるが, gillespieが1つの均一な閉じた空間の中で計算を行っているのに対して, mesoは空間をSubvolumeと呼ばれる小さな直方体に分割し, それぞれのSubvolumeが異なる分子濃度を持つことを許す. 従って上の例では, 一辺が1の立方体を一辺が0.25の立方体64個に分割する.

最初に分子種Cを60個投入しているから, 1つのSubvolume当り高々1個程度のCが含まれることになる. このとき, Cの濃度は最初の場合と同じだが, かい離した後のAの濃度が異なる. かい離したばかりの1つのA分子の濃度は, 元々は$1/1=1$であったが, Subvolumeでは$1/(1/64)=64$となってしまう. 実際にはこの程度の分割数であればここまでの効果は出ないが, 結果とて結合する反応が速くなるため, 上のように結合状態Cの量が多くなる. 別の見方で説明しよう. mesoではかい離直後のAとBは必ず同じSubvolume内にいる. 一方, gillespieでは十分に攪拌された均一な系を仮定しているので, かい離直後のAとB分子は64つのSubvolumeのいずれかに含まれることになる. このときAとBが同じSubvolumeに含まれる確率は$1/64$である. 従ってやはり結合する確率が高くなる.

分子の拡散係数を与える

なぜこのような違いが生じてしまうかと言えば, mesoを使うことで我々は空間を手に入れたが, 一方でまだ分子の拡散運動を考えていないからだ.

これを設定するには, 初級編でやった方法で分子種Speciesの属性値'D'を使う. 前回はadd_species_attributeを使ったが, ReactionRuleでやったのと同様にここでもE-Cell4の特殊記法が利用できる.

with species_attributes():
    A | {'D': '1'}
    B | {'D': '1'}
    C | {'D': '1'}

    # A | B | C | {'D': '1'}  # means the same as above

'species_attributes'を使うことでセパレータ'|'に続いてdict型³で属性を設定できる. ここでは拡散係数を意味する'D'を1に設定した.

さて上記のモデルにこれを加えて再度計算してみよう. 前回よりも計算に時間がかかるとは思うがgillespieのときと似た結果が再び得られたことと思う.

では分子の拡散運動によってなぜ前回の問題が解決されるのだろうか?

拡散係数が$D$の分子の3次元空間における自由な拡散運動について考えよう. 拡散係数の単位は$\mathrm{\mu m}^2/s$や$\mathrm{nm}^2/\mu s$のように長さの二乗を時間で割ったものとなる. このとき, 最初の位置から時間$t$秒後の位置までの距離の二乗は平均すると$6Dt$に等しいことが知られている.

逆に言えば, 長さのスケールが$l$の空間に分子が留まっている平均的な時間のスケールはおよそ$l^2/6D$程度である. 先ほどの例では, Subvolumeの一辺は0.25で拡散係数は1だから, だいたい0.01秒となる. 対して, AとB分子が同じSubvolume内にいても反応するのにかかる時間はだいたい1.5秒であるから, 同じSubvolume内にかい離してもほとんどの場合反応よりも先に拡散して他のSubvolumeへと移ってしまうわけである.　$l$が小さくなればなるほどSubvolumeの容積$l^3$は小さくなり, 従ってかい離後の反応速度は高くなるが, 一方で拡散によってその空間から抜け出すのにかかる時間も小さくなる.

分子の局在

これまでWorldへ分子を加えるのにはodeやgillespieと同じように'add_molecules'関数を用いてきた. これに対してMesoscopicWorldではその空間表現に応じた分子の配置が可能になる.

w = meso.MesoscopicWorld(Real3(1, 1, 1), Integer3(3, 3, 3))
w.add_molecules(Species('A'), 120)
w.add_molecules(Species('B'), 120, Integer3(1, 1, 1))

MesoscopicWorldの'add_molecules'では3つ目の引数としてInteger3を1つだけ与えることでどのSubvolumeにその分子を配置するかを指定することができる.

上の例では分子種Aは空間全体にちらばるが, Bはちょうど中心のSubvolumeだけに配置される⁴. このことを確かめるには'num_molecules'を使えば良い.

print(w.num_molecules(Species('B')))  # will print 120
print(w.num_molecules(Species('B'), Integer3(0, 0, 0)))  # will print 0
print(w.num_molecules(Species('B'), Integer3(1, 1, 1)))  # will print 120

さらに, IPython Notebookを利用している場合はecell4.vizライブラリ⁵を用いることでより直感的に分子の局在を把握することができる.

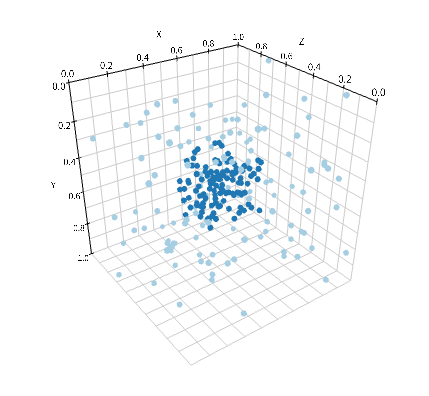
viz.plot_world(w, radius=0.01)

'viz.plot_world'はWorldを与えることでIPython Notebook上で粒子の配置をインタラクティブに表示してくれる⁶. 引数としてradiusを設定して分子の大きさを指定する.

分子の初期配置に局在を与えることができたので, 実際にこれをもとにシミュレーションを行ってみよう. 上の例では拡散係数を1とし, World全体の一辺を1としたので, 十分に攪拌されるには10秒あれば十分であろう. 計算後に再び'viz.plot_world'を呼び出して実際に攪拌されていることを確認しておこう.

分子の初期配置と反応

それでは分子の局在が反応にどのような影響を持つのかを極端な例で確かめる.

from ecell4 import *

with species_attributes():
    A | B | C | {'D': '1'}

with reaction_rules():
    A + B > C | 0.01

m = get_model()
w = meso.MesoscopicWorld(Real3(10, 1, 1), Integer3(10, 1, 1))
w.bind_to(m)

モデルは簡単な結合だけを含む. WorldはX軸方向にだけ長い直方体とした. あとは分子を偏ったかたちで配置する.

w.add_molecules(Species('A'), 1200, Integer3(2, 0, 0))
w.add_molecules(Species('B'), 1200, Integer3(7, 0, 0))
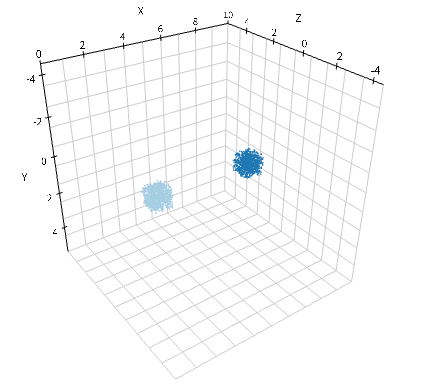
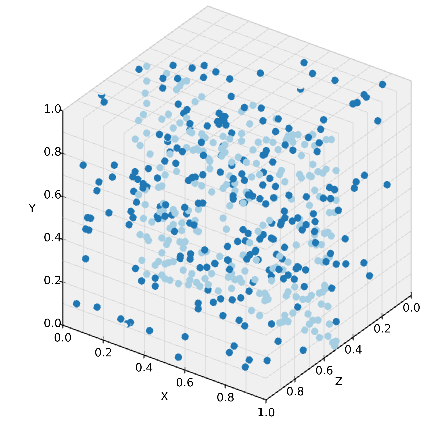
viz.plot_world(w, radius=0.025)

余談だが, ここで'Integer3(0, 0, 0)'と'Integer3(9, 0, 0)'としない理由がある. E-Cell4におけるWorldは基本的にどれも周期境界条件⁷を採用している. 従って, 先の2つのSubvolumeは実は隣あっているからである.

想定した配置が得られていればMesoscopicSimulatorを用いて計算してみよう.

sim = meso.MesoscopicSimulator(w)
obs1 = NumberObserver(('A', 'B', 'C'))  # XXX: saves the numbers after every steps
sim.run(5, obs1)
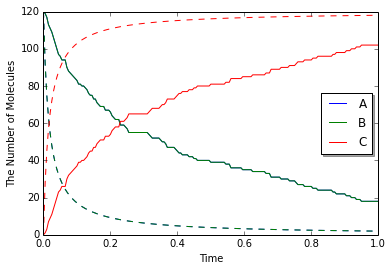
viz.plot_number_observer(obs1)

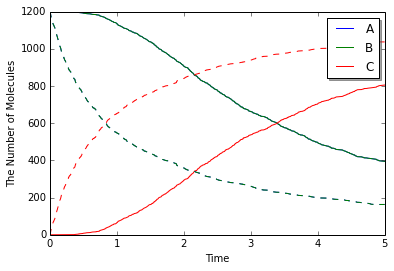
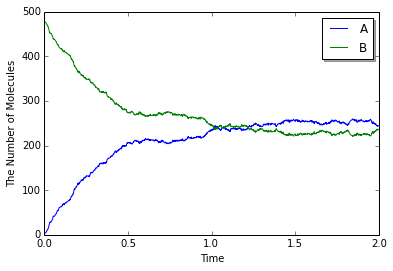
きちんと反応は進んでいただろうか? 結果を確認するために, mesoのままで配置を一様に分布させるようにするか, gillespieモジュールを使って同じモデルを計算させてみる.

実線が偏りがある場合で点線がない場合である. 偏りがある場合は明かに反応に遅れがみられる. さらによく見れば, 時系列の形状も実線と点線では異なっていることに気がつくかもしれない. これはA分子とB分子が拡散によって出会うまでに時間がかかるためだろう. 実際, 初期配置によるA, B間の距離(およそ4)だけ進むのにかかる時間スケールは$4^2/2(D_\mathrm{A}+D_\mathrm{B})=4$秒である.

Spatiocyteによる1分子粒度シミュレーション

空間Gillespie法を用いてE-Cell4における空間表現の一例を説明してきた. 次に, より高解像度な空間表現である'1分子粒度計算'について見ていこう.

微視格子法Spatiocyte

空間Gillespie法では, Gillespie法が通常扱ってきた空間をより小さな空間に分割し, そのSubvolume間での分子の拡散を考えることで空間を取り入れた. しかしながら, そのSubvolumeの中では分子はいまだ数として扱われており, それぞれの分子の位置というのは不確定である. 言いかえれば, この計算手法の空間的解像度はSubvolumeの一辺$l$に等しい. この解像度を高めるには$l$をどんどん小さくしていけば良いが, この手法では$l$は分子の直径$R$に対して十分大きく (少くとも10倍以上)なければならない.

では, 空間解像度を分子の大きさまで高めるにはどうすれば良いだろうか? その答えとして, 分子を何個あるかではなく, 位置をもった各分子の反応拡散運動を直接表現した1分子粒度シミュレーションが挙げられる. E-Cell4では複数の1分子粒度計算技法が利用できるが, ここでは微視格子法Spatiocyteを例にとって説明する^{8 9}.

Spatiocyteは各分子を1個の反応する剛体球とみなして, 六方最密格子¹⁰で表現された空間中を動かす. 空間Gillespie法と違い, 各々の分子には識別番号がふられており, その分子がどこにいるのかを分子の大きさの粒度で知ることができる. 時間スケールで言えば, 拡散による時間スケールは距離の2乗に比例するから, 空間Gillespie法に比べて100倍細かい時間幅となる.

何はともあれ, Spatiocyteを使ってみよう. とはいえ, 基本は今までとまったく同じである.

注意: 以降の例でSpatiocyteにはlatticeという名前が使われているが, 今後の変更でspatiocyteというモジュール名に改められる予定である.

equilibrium4.py

from ecell4 import *

with species_attributes():
    A | B | C | {'D': '1'}

with reaction_rules():
    A + B == C | (0.01, 0.3)

m = get_model()
w = lattice.LatticeWorld(Real3(1, 1, 1), 0.005)  # The second argument is 'voxel_radius'.
w.bind_to(m)
w.add_molecules(Species('C'), 60)
sim = lattice.LatticeSimulator(w)
obs = FixedIntervalNumberObserver(0.1, ('A', 'B', 'C'))
sim.run(10, obs)

違いはLatticeWorldに与えられた2つ目の引数で, これはVoxel半径と呼ばれている. Spatiocyteでは空間を分子大に分割して分子の位置を決めているが, この空間の最小単位をVoxelと呼び, その大きさをVoxel半径で与える. ほとんどの場合, これは分子の大きさとすれば良い. この例では, 一辺が1$\mathrm{\mu m}$の空間中で分子の半径を5$\mathrm{nm}$とした.

計算時間はこれまでより長くかかると思われるが, 結果は言うまでもなくodeやgillespieと一致するだろう.

1分子の拡散運動

では1分子粒度計算を確かめるために実際に1分子を扱ってみよう.

from ecell4 import *

with species_attributes():
    A | {'D': '1'}

m = get_model()
w = lattice.LatticeWorld(Real3(1, 1, 1), 0.005)
w.bind_to(m)

(pid, p), suc = w.new_particle(Species('A'), Real3(0.5, 0.5, 0.5))

'new_particle'関数はLatticeWorldに一つの分子を指定した場所に置く. と同時に, 作った分子の識別番号'pid'と粒子の情報'p'のtupleと無事に配置できたかどうか'suc'を返す. 既にその場所に分子が置かれていれば, 重ねて配置することはできないため, 'suc'はFalseとなって失敗する. 粒子'p'には分子の位置や分子種, 半径, 拡散係数といった情報が含まれている. 今後は識別番号'pid'を使うことで粒子'p'を取り出し, 情報を得ることができる.

実際に確かめてみよう.

pid, p = w.get_particle(pid)
print(p.species().serial())  # will print: A
print(p.radius(), p.D())  # will print: (0.005, 1.0)
print(tuple(p.position()))  # will print: (0.49806291436591293, 0.49652123150307814, 0.5)

'get_particle'関数は識別番号を受け取り, 識別番号と粒子を返す. 当然識別番号は与えたものと同じものである. 粒子からは'position'関数で位置をReal3として取り出せる. そのままでは読みにくいので, tupleに変換してから表示している.

返ってきた位置が指定した場所から少しずれているのはSpatiocyteが分子を格子上にしか配置できないからである. LatticeWorldは与えられた場所から一番近い格子状に分子を置いてくれる. 'viz.plot_world'関数を使えば確かに分子が1個だけ中心に配置されているのがわかる.

この分子の拡散の軌跡を追うためにもObserverが利用できる.

sim = lattice.LatticeSimulator(w)
obs = FixedIntervalTrajectoryObserver(0.002, (pid,))
sim.run(1, obs)
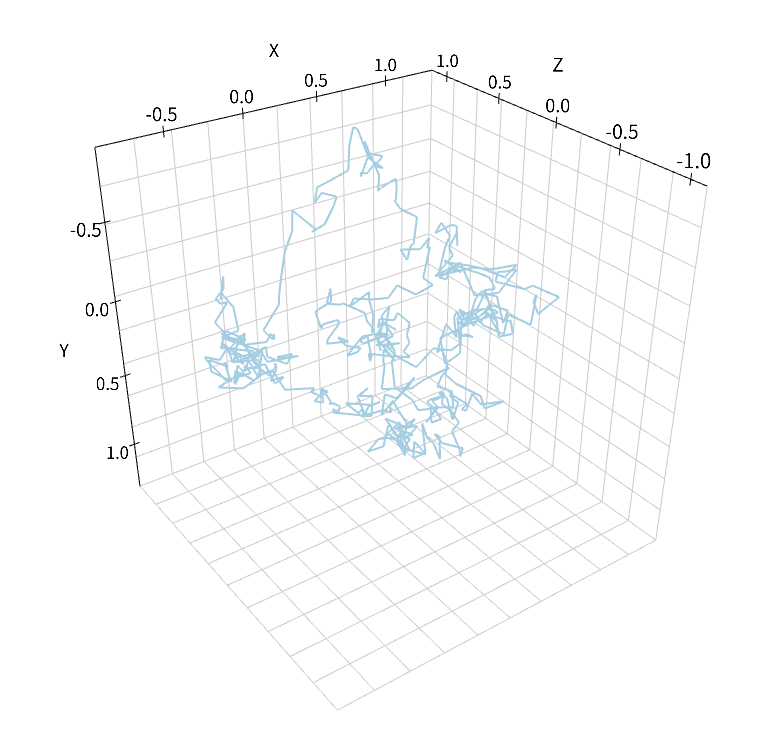
viz.plot_trajectory(obs)

ここでは'viz.plot_trajectory'関数を使って表示させたが, NumberObserverのときと同様に'data'関数によって軌跡をReal3のリストとして取り出すことも可能だ.

print(len(obs.data())) # should return 1
print(len(obs.data()[0])) # should return 501

data関数は入れ子のリストを返す。最初のリストのindexはparticleのindexである。ここでは1つしかparticleを作っていないのでそのindex長は1である。次のリストのindexは最初のリストのparticleに対応するReal3のリストである。ここではsimulationを1秒間runさせ、その軌跡を0.002秒刻みで記録した。そのため 1つのReal3の初期値 と 1/0.002 = 500個のReal3 あわせて501個のReal3が返ってくる。

また, 'add_molecules'関数で追加した分子は識別番号がわからないが, 'list_particles'で分子種から粒子をまとめて引き出すことができる.

w.add_molecules(Species('A'), 5)

particles = w.list_particles(Species('A'))
for pid, p in particles:
    print(p.species().serial(), tuple(p.position()))

'list_particles'関数は, 'add_molecules'関数などと同様に他のWorldでも利用できる¹¹重要な関数なので是非覚えておいてほしい. 余談だが, Spatiocyteでも1分子を扱う正式な関数は本来'list_voxels'であり, 座標はReal3ではなく1つの整数値で表現されている.

拡散係数と二次反応

今まで扱ってきたモデルの結合反応は二次反応とも呼ばれている. Spatiocyteにおいてこの二次反応と拡散係数の関係を見てみよう.

from ecell4 import *

with species_attributes():
    A | B | C | {'D': '1'}

with reaction_rules():
    A + B > C | 1.0

m = get_model()
w = lattice.LatticeWorld(Real3(2, 1, 1), 0.005)
w.bind_to(m)
w.add_molecules(Species('A'), 120)
w.add_molecules(Species('B'), 120)
obs = FixedIntervalNumberObserver(0.005, ('A', 'B', 'C'))
sim = lattice.LatticeSimulator(w)
sim.run(1.0, obs)

%matplotlib inline

odew = ode.ODEWorld(Real3(2, 1, 1))
odew.bind_to(m)
odew.add_molecules(Species('A'), 120)
odew.add_molecules(Species('B'), 120)
odeobs = FixedIntervalNumberObserver(0.005, ('A', 'B', 'C'))
odesim = ode.ODESimulator(odew)
odesim.run(1.0, odeobs)
viz.plot_number_observer(obs, "-", odeobs, "--")

今回はこれまでよりも高い速度定数を使っているがこれまで同様の結果が得られる. しかし, 常微分方程式の結果と詳細に比較してみると異なる結果であることがわかる (下図実線がSpatiocyte, 点線がodeによるもの).

これは何かの誤りだろうか? 実際に速度定数をこれよりもずっと高い値にしたとき, odeでは際限なく反応速度ははやまるが, Spatiocyteではこれ以上ほとんど速くならない.

これはこれまでのソルバと1分子粒度計算技法における反応速度定数の定義の違いから生じている. 前者は巨視的なmacroscopic, もしくは実効的なeffective反応速度定数と呼ばれるものであるのに対し, 後者は微視的なmicroscopic, もしくは内在的なintrinsic反応速度定数と呼ばれるものである.

巨視的な反応速度定数は分子を混ぜ合わせたときに反応の起こる速さを表しているのに対し, 微視的な反応速度定数とは実際に分子が衝突した際にどの程度の反応性があるかを表すものである. 従って, 微視的な見方では反応する前にまず衝突しなければならない. Spatiocyteではこの微視的な速度定数をいくら速くしても拡散によって起こる衝突の速さ以上に速く反応させることはできない. こうした状況を拡散律速と呼ぶ. これは空間的Gillespie法において偏って配置された分子同士が反応するまでに時間を要したことと良く似ている.

この巨視的な速度定数$k_\mathrm{on}$と微視的な速度定数$k_a$の間には三次元空間で以下の関係が知られている¹².

\frac{1}{k_\mathrm{on}}=\frac{1}{k_a}+\frac{1}{4\pi RD_\mathrm{tot}}

ここで$R$は衝突する二つの分子の半径の和であり, $D_\mathrm{tot}$は拡散係数の和である. 上の例では右辺第二項$k_D=4\pi RD_\mathrm{tot}$はおよそ0.25であるから微視的な反応速度定数1.0とあわせて, 巨視的な反応速度定数はおよそ0.2となる¹³.

このように良く攪拌された系を仮定する (すなわち, 拡散係数が無限である)常微分方程式やGillespie法による計算と違い, 1分子粒度計算では分子の拡散と反応がきちんと分離できる. ただし, 上の式でも分かる通り, 微視的速度定数が$k_D$に対して十分小さければ巨視的速度定数とほとんど一致する (反応律速).

Spatiocyteにおける構造体の扱い

最後にSpatiocyteを用いて細胞膜などの構造体を扱う方法について説明する. E-Cell4において, 構造体はまだまだ開発段階だが, Spatiocyteではある程度その機能が利用できる.

現在扱うことのできる形は限られているが, 例としてまず球体をみてみよう. 分子の動きを球状の空間に制限するためにまず球状の構造体を作る.

w = lattice.LatticeWorld(Real3(1, 1, 1), 0.005)
sph = Sphere(Real3(0.5, 0.5, 0.5), 0.45)
print(w.add_structure(Species('C'), sph))  # will print 539805
viz.plot_world(w)

'Sphere'は1つ目の引数を中心として2つ目の引数を半径とする球を意味する. これに'C'というSpeciesを与えてWorldに追加した.

Spatiocyteでは構造体は, 空間内の領域を特殊なVoxelで埋め尽くすことによって表現される. 上の例で言えば指定した球体内のVoxelはすべてCという分子種で占められている. 'viz.plot_world'で表示してみると実際に球状に分布しているのがわかる. ただし, 分子数はおよそ54万個と表示するには多すぎるため, 一部だけをプロットしているが, 実際には完全に埋まっている.

球ができたところで, この球の中だけを動き回る分子を作る. そのためには'location'属性を指定する.

with species_attributes():
    A | {'D': '1', 'location': 'C'}

m = get_model()

あとはいつもと同様に分子を'add_molecules'すれば良い.

w.bind_to(m)
w.add_molecules(Species('A'), 120)
viz.plot_world(w, species_list=('A',))  # visualize A-molecules only

これで分子種Aは分子種Cの構造体の上に存在すると指定したので, 実際に'add_molecules'でも球体内にのみ配置される. 注意点として当然だが, Aを加えるよりも前に構造体を作っておく必要がある.

この分子種Aの運動が本当に球体内に制限されているかを確認してみよう. これにもやはり'FixedIntervalTrajectoryObserver'が使える.

pid_list = [pid for pid, p in w.list_particles(Species('A'))[: 10]]
obs = FixedIntervalTrajectoryObserver(1e-3, pid_list)
sim = lattice.LatticeSimulator(w)
sim.run(1, obs)
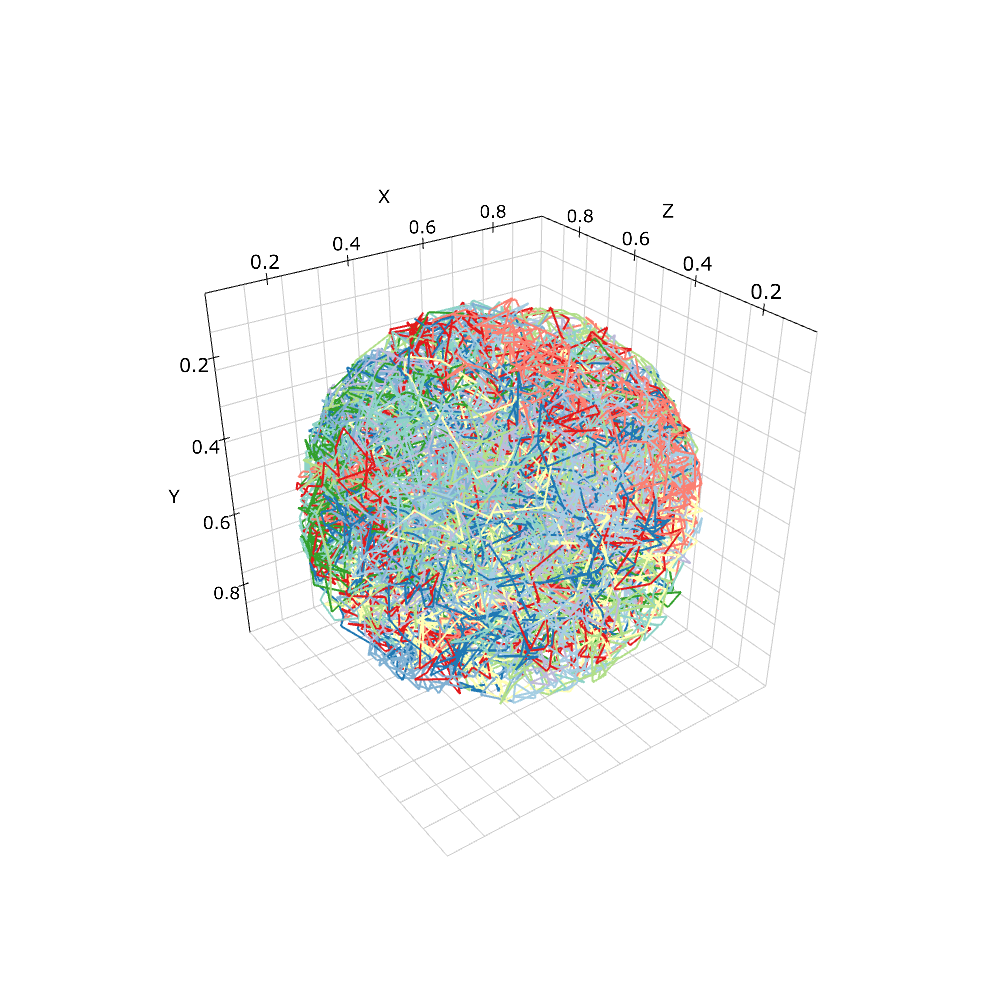
viz.plot_trajectory(obs)

'pid_list'は60個のA分子のうち適当な10個の識別番号のリストである. これら10個の分子の拡散の軌跡に色を付けた. 確かに球体内に運動が制限されていることがわかる.

構造体と反応

最後に構造体間の分子の移行について説明しておこう. まず, 'location'属性が指定されていない分子種はどの構造体にも属さない. 先の例で言えば, 'location'を指定しなければ球の外側に配置される.

では平面を例にとって実際に試してみよう. まず平面を作るには原点 'origin'と二つの軸ベクトル 'unit0', 'unit1'の3つのReal3を用いて以下のようにして作ることができる.

ps = PlanarSurface(origin, unit0, unit1)

これを利用して平面上の分子種Aと通常の分子種Bを想定すると,

from ecell4 import *

with species_attributes():
    A | {'D': '0.1', 'location': 'M'}
    B | {'D': '1'}

m  = get_model()

w = lattice.LatticeWorld(Real3(1, 1, 1))
w.bind_to(m)

origin = Real3(0, 0, 0.5)
unit0 = Real3(1, 0, 0)
unit1 = Real3(0, 1, 0)
w.add_structure(
    Species('M'), PlanarSurface(origin, unit0, unit1))  # Create a structure first

w.add_molecules(Species('B'), 480)  # Throw-in B-molecules
viz.plot_world(w, species_list=('A', 'B'))

少々わかりにくいが, 平面上以外だけにB分子が配置される. では, このB分子が平面Mに吸着してA分子となる反応はどう表現すれば良いか.

with reaction_rules():
    B + M == A | (1e-3, 1.5)

意味するところは見ての通りで, B分子が構造体Mと衝突したときに吸着してA分子となる. 逆にまたA分子はかい離してもとの平面とB分子になる.

ここまでくれば後はいつも通りにSimulatorで計算できる.

sim = lattice.LatticeSimulator(w)
obs = NumberObserver(('A', 'B'))
sim.run(2, obs)

viz.plot_number_observer(obs)
viz.plot_world(w, species_list=('A', 'B'))

ちなみに構造体からのかい離では構造体の分子種は省略できるが, 結合では省略できない. 生成物であるA分子を配置すべきMがまわりに無い状況でBからAを作ろうと思っても不可能だからだ. 逆に今回の場合, A分子は平面M上のどこにあってもB分子を配置できるので問題ないわけだ. さらに言えば, かい離の場合は構造体を省略してもしなくても一次反応であることに変わりないが, 結合では二次反応が一次反応になり, 速度定数の意味も変わってしまう.

with reaction_rules():
    B + M > A | 1e-3
    A > B | 3.0  # means the same as A > B + M

練習問題

1. 空間Gillespie法に関する練習: 空間Gillespie法で一辺が$l$のSubvolumeの場合について拡散の時間スケールを計算した. 一方でかい離直後の分子が再び結合するのにかかる時間スケールについても説明した. この2つの時間スケールの$l$に対する依存性について考え, $l$が満すべき条件について明かにする. ただし, 空間Gillespie法では$l$について下記の条件を満すべきことが知られている.

R^2 \ll l^2 \ll 6D\tau_\mathrm{min}

    ここで, $R$は分子の直径 (より正確には反応半径), $\tau_\mathrm{min}$は分子の各反応に対するもっとも短かい平均寿命 shortest life-timeを表わす[^Elf04].

[^Elf04]: Elf J. and Ehrenberg M., "Spontaneous separation of bi-stable biochemical systems into spatial domains of opposite phases", Syst. Biol., 1(2), 230-236 (2004)

1. 分子の初期配置に関する練習: 上の例を改変して, AB分子の初期配置, 反応速度定数や拡散係数といったパラメータを様々に変えて反応にどのような影響があるか調べる. また, 空間均一なGillespie法を使って上の例のような時系列を再現するモデルを作ることができないだろうか?

1. 分子の拡散に関する練習: 三次元における自由拡散の場合, 拡散係数$D$の分子の$t$秒後の位置までの平均二乗距離 Mean Square Displacementは

    ```math
\left<L^2\right>=6Dt

となることが知られている. 実際Spatiocyteでもそうなっているだろうか?

1. 巨視的と微視的速度定数に関する練習: 巨視的にせよ微視的にせよ速度定数の単位は同じ$\mathrm{nM}^{-1}s^{-1}$や$\mathrm{\mu m}^3s^{-1}$である. 拡散速度が1$\mathrm{\mu m}^2/s$で, 直径が5$\mathrm{nm}$の二つの分子の衝突速度定数$k_D$は何$\mathrm{nM}^{-1}s^{-1}$であるか?

2. 構造体に関する練習: 平面の構造体を使って, 平面上での拡散係数$D$とその平均二乗距離の関係について確かめる.

1. より正しくはthe Next Subvolume Methodに近い. 詳しくは論文を参考のこと. ↩

2. ’Integer3’は’Real3’と同じ3次元ベクトルだが要素が実数Realではなく整数値Integerとなっている. ↩

3. http://docs.python.jp/2/library/stdtypes.html#typesmapping ↩

4. 座標は0はじまりであるため, Integer3(1, 1, 1)は各軸方向に2つ目のSubvolumeとなる. ↩

5. Using Elegans: https://github.com/domitry/elegans ↩

6. 分子が粒子として表示されるが, MesoscopicWorldでは実際にはSubvolume内のどこに存在するのか具体的な位置があるわけではない. そのため, Subvolume内に毎度ランダムに配置される. ↩

7. periodic boundary condition. 簡単に言えばある軸に注目した場合に, 分子が右端を超えたとき左端がら出てくる, かつその逆であるとみなされるということ. ↩

8. Arjunan S.N.V. and Tomita M. "A new multicompartmental reaction-diffusion modeling method links transient membrane attachment of E. coli MinE to E-ring formation", Syst. Synth. Biol., 4(1), 35–53 (2010). ↩

9. http://spatiocyte.org/ ↩

10. http://ja.wikipedia.org/wiki/六方最密充填構造 ↩

11. ただし, ODEWorldでは利用できない. ↩

12. Smoluchowski–Collins–Kimballの式. ↩

13. ただし, Spatiocyteでは特別な設定を行わなければ, 二次の反応速度定数は$3\sqrt{2} RD$よりも遅くなければならず, 衝突速度定数$k_D$も$3\sqrt{2} RD$である. ↩