準備
インストールについては別記事にありますのでそちらを参考にして下さい.
本記事は上級編です. 初・中級編を理解していることを前提とします.
また本記事ではIPython Notebookの利用を前提とする部分があります.
使い方
もはや「簡単な」使い方ではなくなってきている気がするが, 最後により高度な機能について少し説明したい.
ルールベース・モデリング
分子種に構造を持たせる
これまでの分子種の名前は単なる記号であった.
例えば, A > Bという反応を考えたとき, 多くの場合分種種Aがなんらの修飾状態や構造の変化によって分子種Bになるのであって分子としては同じ分子であると考えられる. しかし分子種AやBといった場合その分子種間の関係性は明らかではない. もう一つ例を挙げよう. A + A > Bという反応ではおそらく分子種BはA分子が2分子結合した二量体だろうと予想できるがBという名前からはわからないし, たとえ'B'を'A2'という名前に変えたとしても計算機には判断できない.
こうした問題に対して, 分子種に構造を与えるのがルールベース・モデリングの第一歩である. 以下で実際にE-Cell4を用いてルールベース・モデリングを体験していこう.
with reaction_rules():
X(s=u) > X(s=p) | 1 # corresponding to 'A > B | 1'
E-Cell4では括弧や等号を使って分子種の構造を決めていく. 上の例でX(s=u)とX(s=p)が各々分子種名を表す. ここで分子種X(s=u)は'X'という分子の修飾's'が状態'u'であるものを意味する. 同様に分子種X(s=p)は'X'という分子の修飾's'が状態'p'であるものになる. ようするにこの反応では分子'X'が修飾's'の状態を'u'から'p'に変えることを意味する. これが分子種の構造になる.
このことを確かめるのにWorldを使ってみよう.
from ecell4 import *
w = gillespie.GillespieWorld(Real3(1, 1, 1))
w.add_molecules(Species('X(s=u)'), 60)
w.add_molecules(Species('X(s=p)'), 120)
print(w.num_molecules(Species('X(s=u)'))) # will print 60
print(w.num_molecules(Species('X(s=p)'))) # will print 120
先ほどの分子種を各々60個, 120個追加して数を数えている. 分子種の書き方を変えてもいつもと同じで追加した数が得られる. では以下のようにしたらどうなるだろうか.
print(w.num_molecules(Species('X'))) # will print 180
ここで分子種'X'の数を数えてみたが, 我々は'X'という分子種は1つも追加していない. にもかかわらず180個という数が得られた. これは'X'という名前の分子種ではなく, 'X'という分子を修飾状態に関わらず全て数え上げているためである. 最初に加えた2つの分子種はどちらも'X'という名前であり, 修飾状態だけが異なる. 従って, 'X'を数えた場合どちらも当てはまるのである.
ちなみに, きっちり'X'という名前の分子種だけを数えたい場合はnum_molecules_exactを使おう. 今回はそのような分子種は存在しないので0が得られるはずである.
次に結合を考える. 'X'という分子と'Y'という分子が結合した複合体を表す分子種は以下のように書ける.
with reaction_rules():
X(b1) + Y(b2) > X(b1^1).Y(b2^1) | 1
この反応の右辺を見てもらいたい. 'X'と'Y'がドット'.'で結合されているのがわかると思う. このように複合体は複数の分子種をドットでつないで表現する.
ところでX(b1^1).Y(b2^1)は全体として一つの分子種を表しているが中には'X(b1^1)'と'Y(b2^1)'という二つの要素が含まれているのがわかる. E-Cell4ではこれらを単位分子種 Unit Speciesと呼ぶ. X(b1^1).Y(b2^1)は二つの単位分子種を含む分子種である. もちろん, X(p=u)であれば一つの単位分子種からできている.
話を戻すと, X(b1^1).Y(b2^1)の単位分子種にはそれぞれ'b1', 'b2'という修飾が付与されている. これによって単位分子種間の結合箇所を決めている. 'X'と'Y'はそれぞれの修飾'b1', 'b2'によってつながっている. 記号'^'の後の数字は結合箇所の対応を表す数字である. これは対応さえ取れていれば, 0より大きなどんな数字でも良い. また今回は修飾に'b1', 'b2'と異なる名前をつけたが別に同じでも良い.
左辺のX(b1)で修飾'b1'に等号による状態も'^'による結合も記されていないのは, 結合箇所'b1'が誰とも結合していないことを明らかにするためだ. X(b1)は修飾'b1'を介して誰とも結合していない'X'を意味している.
複合体の表現を説明したところで先ほどと同じように試してみよう.
w.add_molecules(Species('X(b1)'), 10)
w.add_molecules(Species('Y(b2)'), 20)
w.add_molecules(Species('X(b1^1).Y(b2^1)'), 30)
print(w.num_molecules(Species('X'))) # will print 40
print(w.num_molecules(Species('Y'))) # will print 50
print(w.num_molecules(Species('X.Y'))) # will print 30
最後に注意点だが, 結合部位と修飾部位を両方もつ分子種の場合, X(a, b=c)とは書けるがX(b=c, a)とは書けない. 部位が複数ある場合もX(a, b, c, d=e, f=g)のように書く必要がある. ただし, 順番を入れ替えたX(c, a, b, f=g, d=e)は先ほどと同じ意味で使える.
反応則
先の例では分子種に構造を与えることで分子数を数えることができるようになった. 例えば, 数えるときに与えた分子種'X'は具体的な分子種を意味するのではなく, 数えるべき具体的な分子種の条件, つまり単位分子種にXを含むもの, を決めた一種のパターンである. このようなパターンを反応を記述する際にも活かそうというのがルールベース・モデリングの次のステップである.
1つの単位分子種Xからなる簡単な例を考えてみよう.
例えば, 単位分子種Xには3つのリン酸化部位's1', 's2', 's3'があり, 各々'u'か'p'の二状態のいずれかを独立に取り得るものとする. このとき単位分子種Xのとりえる状態数は$2^3=8$状態となる.
さてこのような分子Xのリン酸化反応はどのように書けばよいか. 実は以下のようになる.
with reaction_rules():
X(s1=u, s2=u, s3=u) > X(s1=p, s2=u, s3=u) | 1
X(s1=u, s2=p, s3=u) > X(s1=p, s2=p, s3=u) | 1
X(s1=u, s2=u, s3=p) > X(s1=p, s2=u, s3=p) | 1
X(s1=u, s2=p, s3=p) > X(s1=p, s2=p, s3=p) | 1
X(s1=u, s2=u, s3=u) > X(s1=u, s2=p, s3=u) | 2
X(s1=p, s2=u, s3=u) > X(s1=p, s2=p, s3=u) | 2
X(s1=u, s2=u, s3=p) > X(s1=u, s2=p, s3=p) | 2
X(s1=p, s2=u, s3=p) > X(s1=p, s2=p, s3=p) | 2
X(s1=u, s2=u, s3=u) > X(s1=u, s2=u, s3=p) | 3
X(s1=u, s2=p, s3=u) > X(s1=u, s2=p, s3=p) | 3
X(s1=p, s2=u, s3=u) > X(s1=p, s2=u, s3=p) | 3
X(s1=p, s2=p, s3=u) > X(s1=p, s2=p, s3=p) | 3
これが意味するところをきちんと把握し, 誤り無く書くのは容易ではない. なぜこのように面倒になるかと言えば, 各リン酸化反応が独立であることが活かされず, 1つのリン酸化部位を考えるのに他の全ての状態を数え上げなければならないからである.
そこで分子種のパターンで考えてみよう. リン酸化部位's1'に着目したとき, リン酸化反応とは分子Xの's1'の状態が'u'から'p'から変わることである. すなわち, 's1'の状態が'u'になる分子Xのパターンに当てはまる分子をとってきて, 状態を'p'に変えれば十分である.
with reaction_rules():
X(s1=u) > X(s1=p) | 1
X(s2=u) > X(s2=p) | 2
X(s3=u) > X(s3=p) | 3
これらは個々の具体的な分子種を左右に持った反応ではなく, 分子種のパターンを与えるものであるから反応則 Reaction Ruleと呼ぶ. このモデルを利用するためにはこれまでとは異なり, 反応則によるモデルであることを指示しなければならない.
さらに, 反応則はあくまでもパターンに基づいたルールでしかないため, これだけでは実際にどんな分子種があるのかはわからない. 上の例で言えば左辺に'X(s1=u)'という分子種が現れたからといってそれが実在するとは限らない. 最初に想定したのは'X(s1=u, s2=u, s3=u)'といった3つの修飾をもった分子種であったことを思い出してほしい.
ルールベース・モデルでは種 seedとなる分子種を与えることでそこから繰り返し反応則を適用して出来うるすべての分子種を芋づる的に生成する. ここで種となる分子種とは, 後でWorldに追加する分子種だと思えば良い.
m = get_model(seeds=(Species('X(s1=u, s2=u, s3=u)'),))
print(len(m.species_attributes())) # will print 8
print(len(m.reaction_rules())) # will print 12
ここで与えた'X(s1=u, s2=u, s3=u)'という種から8通りの分子種と12の反応が望み通りに得られることがわかる.
最後にこのモデルを使って計算してみよう.
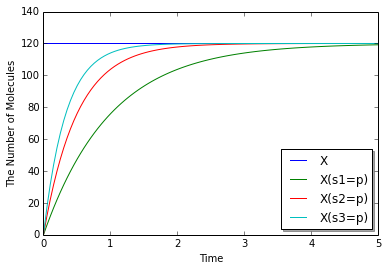
y = run_simulation(
numpy.linspace(0, 5, 100),
{'X(s1=u,s2=u,s3=u)': 120},
model=m,
species_list=('X', 'X(s1=p)', 'X(s2=p)', 'X(s3=p)'))
'species_list'を指定して記録する分子種を決めている. 実際に修飾's1', 's2', 's3'のリン酸化状態だけを見るとそれぞれ指定した速度定数で増えているのがわかる. 当然'X'分子の総量は一定である.
ワイルド・カード
これで基本的な使い方はわかったと思うが, もうひとつだけ覚えるべきことがある. それがワイルド・カードで, E-Cell4では記号'_'で表される.
まず最も重要な使い方は結合に関するものである. 例えば分子種'A'に結合部位'b'があったとき, 誰とも結合していないAの数が知りたければ, A(b)とすれば良い. では, 誰かしらと結合しているAはどのように表現すればよいのだろうか?
with reaction_rules():
A(b) + B(b) > A(b^1).B(b^1) | 1
A(b^_, s=u) > A(b^_, s=p) | 2
m = get_model(seeds=(Species('A(b, s=u)'),))
2つ目の反応則に注目してもらいたい. A(b^_, s=u)と書かれているのがそれである. '_'がワイルド・カード, すなわちどんなものとも合致する記号である. 2つ目の反応則は修飾's'を'u'から'p'に変えるが, この反応がAが誰かと結合しているときにしか起こらないことを意味している.
単に誰かしらと結合しているAであればA(b^_)と書けば良い.
このワイルドカードは結合だけでなく, 修飾にももちろん使える. 簡単な例はA(s=_)で, 修飾's'の状態が何であっても良いことを意味する. 何であっても良いならば書く必要ない気もするが, Aに's'という修飾があることを保証する.
もうひとつ重要なのは単位分子種名に使う場合である. _(s=u)と書けば修飾's'を持ち, それが状態'u'にある分子ならば何でもということになる. ちょっと試してみよう.
from ecell4 import *
with reaction_rules():
_(s=u) > _(s=p) | 1
m = get_model(seeds=(
Species('A(s=u)'), Species('B(s=u)'), Species('C(b^1,s=u).C(b^1,s=u)')))
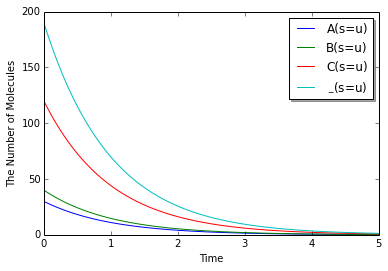
y = run_simulation(
numpy.linspace(0, 5, 100),
{'A(s=u)': 30, 'B(s=u)': 40, 'C(b^1,s=u).C(b^1,s=u)': 60},
model=m,
species_list=('A(s=u)', 'B(s=u)', 'C(s=u)', '_(s=u)'))
単位分子種名が'A'でも'B'でも'C'でも適用されることがわかる. 複合体を形成している場合はその各々にも適応される. もちろん, Observerやnum_moleculesでも利用できる.
分子種の属性を決める場合にもワイルドカードが使える.
with species_attributes():
_ | {'D': '1', 'radius': '0.005'}
分子種いちいちについて同じ属性を指定しなくてもワイルドカードを利用することで全ての分子種の属性を指定できる. 例外を追加する場合はこれより先に指定しておけばよい.
動画を作成する
Worldの状態を簡単に可視化するのにはviz.plot_worldが使えました. ここでは動画を作成する方法を説明する. 動画を作成する方法にはいくつかあるが, 今回はParaViewを利用しよう.
まずは上記のサイトからParaViewをダウンロードし, インストールする. 以下ではParaView-4.3.1-Windows-32bit.exeを使っています.
粒子の位置を記録する
まずは可視化するためのデータを記録する. これにもやはりObserverが使える.
今回は以下のようなモデルを使うことにしよう.
from ecell4 import *
with species_attributes():
A | {'D': '1', 'location': 'C'}
B | {'D': '1', 'location': 'N'}
N | {'location': 'C'}
with reaction_rules():
A + N > B | 1e-4
B + C > A | 1e-4
m = get_model()
w = lattice.LatticeWorld(Real3(1, 1, 1), 0.005)
w.bind_to(m)
w.add_structure(Species('C'), Sphere(Real3(0.5, 0.5, 0.5), 0.441))
w.add_structure(Species('N'), Sphere(Real3(0.5, 0.5, 0.5), 0.350))
w.add_molecules(Species('A'), 720)
入れ子の球を構造体として作り, 外側から内側へ流れ込むようなモデルを考えている. 内側の球であるNは外側の球Cの上に重ねるように配置される.
これから1秒間の計算を実行するのに0.01秒毎に分子種'A'と'B'を選んでその位置をCSV形式で記録する. とはいえ, 手順は基本的にこれまでと同じです.
sim = lattice.LatticeSimulator(w)
obs1 = NumberObserver(('A', 'B'))
obs2 = FixedIntervalCSVObserver(0.01, 'sample%03d.csv', ('A', 'B'))
sim.run(1, (obs1, obs2))
今回は二つのObserverを同時に利用しています. このうち, CSV形式での記録にはFixedIntervalCSVObserverを使います. 引数は, 記録する時間幅, ファイル名, 分子種のリストです. ファイル名には%03dにするとファイル番号を含めることができます.
以上を実行すると'sample000.csv'から'sample100.csv'までができるはずです. ファイルはPythonを実行した場所か, IPython Notebookを使っている場合はサーバー側のIPython Notebookを起動したディレクトリ下に保存されるはずです.
ParaViewによる可視化
ParaViewそのものの説明は直接下記のサイトを参考にしてもらうとしてここではE-Cell4の結果の可視化だけを説明しよう.
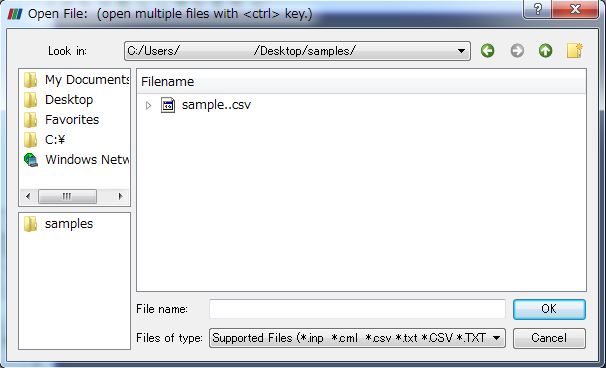
まず, File->Openで保存したCSV形式のデータを選択する. 保存した連番のファイルは下図のようにまとめて表示される. 読み込んだら左下にあるPropertiesでApplyボタンを押すと読み込みが完了する.
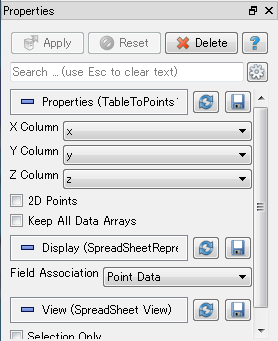
読み込んだ後はPipelineによってデータを可視化していく. 最初にCSVテーブルから座標に変換する. Filters->Alphabetical->Table To Pointsを選択します. 左下からX, Y, Z Columnとしてそれぞれx, y, zを選択した後, Applyボタンを押して下さい.
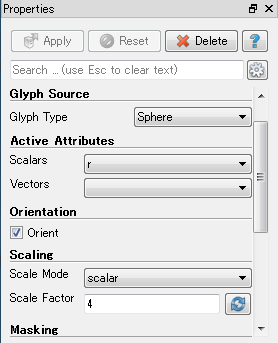
最後にFilters->Common->Glyphを選択します. 先ほどと同様に左下のPropertiesからGlyph TypeをSphereに, Scale Modeをscalarにして下のScale Factor横のReset using current data valuesとヒントの出るボタンを押す. 何か数値が設定されると思うが無視して今回は4を入力したらApplyボタンを押そう.
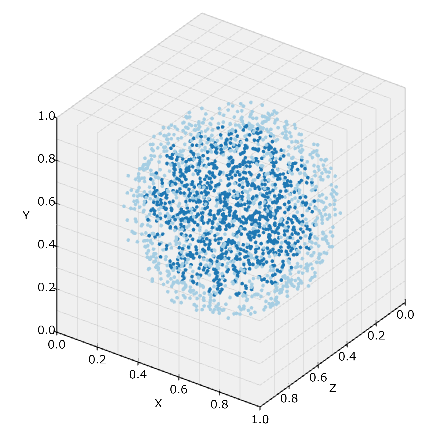
すると先ほどのPropertiesにColoringという項目が増えるので, sidを選んでおく. これで下のような可視化が出来ているはずだ. 何も見えなければ左上のPipeline BrowserでGlyph1の左の目玉がアクティブになっていることを確認しよう.
ここまでできたら後は上のPlayボタンを押す. きちんと赤色が増える様子が確認できたら完成だ. File->Save Animation...から動画が保存できるはずです.
その他のヒント
Factoryの利用
E-Cell4のモジュール切り替えをより容易に行うための書き方について説明する. プログラミングが苦手な方は飛ばしてくれても構わない.
ode, gillespie, meso, latticeのモジュールを使いわけるときの違いはほとんどWorldを作るときだけ表われることに気がつかれたかもしれない. しかしながら, 実際にはSimulatorの名称も違い, Worldを作る際に2つ目の引数があるときとないときがある. こうした問題を解消するため, 各モジュールはFactoryと呼ばれる便利クラスを用意している.
f = ode.ODEFactory()
# f = gillespie.GillespieFactory()
# f = meso.MesoscopicFactory(Integer3(4, 4, 4))
# f = lattice.LatticeFactory(0.005)
w = f.create_world(Real3(1, 1, 1)) # XXX: Factory
w.bind_to(m)
w.add_molecules(Species('C'), 60)
sim = f.create_simulator(w) # XXX: Factory
obs = FixedIntervalNumberObserver(0.1, ('A', 'B', 'C'))
sim.run(10, obs)
こうすることでFactoryを切り替えることでモジュールが切り替えられるようになった. さらに, これを関数化することで簡単に比較できるようにしよう.
from ecell4 import *
def run(m, f):
w = f.create_world(Real3(1, 1, 1)) # XXX: Factory
w.bind_to(m)
w.add_molecules(Species('C'), 60)
sim = f.create_simulator(w) # XXX: Factory
obs = FixedIntervalNumberObserver(0.1, ('A', 'B', 'C'))
sim.run(10, obs)
return obs
with species_attributes():
A | B | C | {'D': '1'}
with reaction_rules():
A + B == C | (0.01, 0.3)
m = get_model()
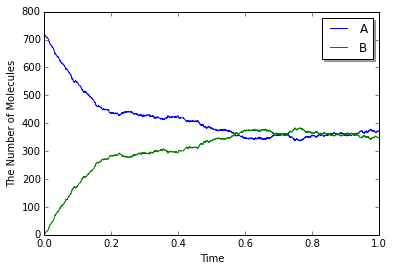
obs1 = run(m, lattice.LatticeFactory(0.005))
obs2 = run(m, ode.ODEFactory())
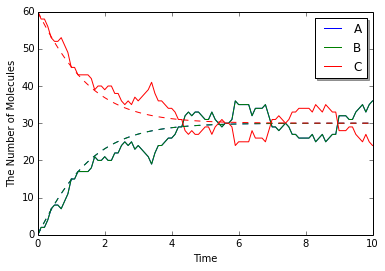
viz.plot_number_observer(obs1, '-', obs2, '--')
もちろんWorldの持つすべての関数が共通に利用できるわけではないが, Factoryを利用することでよりアルゴリズムを問題から分離しやすくなる.
練習問題
-
ルールベース・モデリングにおける分子種の練習. 2つのX分子からなる二量体はどのように表現すればよいか. また, Xの数を数えるときの扱いに関して試す.
-
ルールベース・モデリングにおける反応則の練習. 二種類の単位分子種'X'と'Y'があり, 以下の反応が独立に成立するとき, 何通りの分子種が存在するか?
- X同士は二量体を形成する.
- XとYは結合する.
- Yには1つ修飾部位があり, 2種類の状態のいずれかをとる.
ただし, 対称性に注意せよ.
-
分子の位置の記録に関する練習. 今回,
FixedIntervalCSVObserverでCSV形式のファイルに記録したが, テキストエディタや表計算ソフトなどで開いてみて実際にどのようなことが書き込まれているのか確認しよう. -
ParaViewによる可視化に関する練習. ParaViewは設定によって色々と見栄えが変えられるので自分好みの動画を作ってみる.