LoginSignup
7
6

More than 5 years have passed since last update.

@kaityo256(ロボ太)

Runge–Kutta法を関数オブジェクトで

Last updated at Posted at 2017-02-21

はじめに

いくつかの微分方程式系を、何種類かの数値積分手法で解きたい、というニーズがあった。関数ポインタや仮想関数使うと速度ペナルティがありそう。というわけで関数オブジェクトでなんとかしてみる。Boostにはodeintというそのものズバリのライブラリがあるらしいんだけど、まぁあそこまで実装を隠蔽されてしまうとアレなので自分で組んでみよう。ここでは数値積分手法としては普通の4次のRunge-Kuttaと1次のEuler法を、系としてはロトカ・ヴォルテラ系と調和振動子系を考える。

理想としては、変数をまとめたクラスVars、微分を与える関数diffがあるとして、Runge-Kutta法の1ステップが

  Vars k1 = diff(v);
  Vars k2 = diff(v + k1 * hdt);
  Vars k3 = diff(v + k2 * hdt);
  Vars k4 = diff(v + k3 * dt);
  v = v + (k1 + k2 * 2.0 + k3 * 2.0 + k4) * (dt / 6.0);

みたいに書けて、しかも数値積分のループが、数値積分手法をfとして

  for (int i = 0; i < 200; i++) {
    t += dt;
    v = f(v);
    ofs << t << " ";
    ofs << v.x << " ";
    ofs << v.y << " ";
    ofs << h(v) << std::endl;
  }

みたいに書けて、しかもループ内に(IO以外の)いかなる関数呼び出しもVarsのコンストラクタも呼ばれないようになって欲しい。

で、そういうのを書いた。コードは

においてある。

ロトカ・ヴォルテラ系

ロトカ・ヴォルテラ系について必要なことはWikipediaに書いてある。とりあえず微分方程式は以下のような形になっている。

\frac{dx}{dt} = ax - bxy

\frac{dy}{dt} = cxy - dy

この方程式は$dy/dx$を計算してみるとすぐにわかるように変数分離型になっており、したがって保存量(第一積分)がある。保存量は以下の形をしている。

H = cx + by - d \log x - a \log y

保存量の存在は数値積分の精度を確認するのに便利である。

調和振動子系

調和振動子系は簡単なので説明不要だろう。

\frac{dx}{dt} = - y 

\frac{dy}{dt} = x

で表される系で、以下が保存量になる。

H = x^2/2 + y^2/2

系の定義

まず変数だが、とりあえず今回は$(x,y)$の二変数決め打ちにしてしまう。必要な演算だけオーバーロードしておく。

struct Vars {
  double x;
  double y;
  Vars (double nx, double ny) {
    x = nx;
    y = ny;
  }
  Vars () {
    x = 0.0;
    y = 0.0;
  }
  Vars operator+(const Vars &v) {
    return Vars(x + v.x, y + v.y);
  }
  Vars operator*(const double f) {
    return Vars(x * f, y * f);
  }
};

次は系の定義。系の定義には、状態を与えられた時、その状態での微分係数と保存量を返す関数オブジェクトがあればいいだろう。例えば調和振動子ならこういう形になるかと思う。

class HarmonicOscillator {
public:
  class Diff {
  public:
    Vars operator()(Vars s) {
      Vars dx;
      dx.x = - s.y;
      dx.y = s.x;
      return dx;
    }
  };
  class H {
  public:
    double operator()(Vars v) {
      return v.x * v.x + v.y * v.y;
    }
  };
};

ロトカ・ヴォルテラ系はDiffとHの中身を書き換えるだけなので簡単。

数値積分手法

数値積分手法の関数オブジェクトを作る。数値積分手法にはタイムステップや微分係数を得る手段が必要なので、それを渡す。例えばRunge-Kuttaならこうなる。

template <class DIFF>
class RungeKutta {
private:
  const double dt;
  const double hdt;
  DIFF diff;
public:
  RungeKutta(double _dt) : dt(_dt), hdt(_dt * 0.5) {};
  Vars operator()(Vars v) {
    Vars k1 = diff(v);
    Vars k2 = diff(v + k1 * hdt);
    Vars k3 = diff(v + k2 * hdt);
    Vars k4 = diff(v + k3 * dt);
    v = v + (k1 + k2 * 2.0 + k3 * 2.0 + k4) * (dt / 6.0);
    return v;
  }
};

コンストラクタでタイムステップを渡しており、微分係数はテンプレートとして定義されている。1

例えば

RungeKutta<LotkaVolterra::Diff> rk(dt);

などとすれば、時間刻みdtで、ロトカ・ヴォルテラ系を解くためのRunge-Kuttaスキームが実体化される。

数値積分

ついでに、数値積分のループも抽象化しよう。適当に初期化して、受け取った手法で時間発展させ、時間と変数と保存量を出力するルーチンを作る。手法と保存量を受け取るテンプレートにしてみる。こんな感じ？

template <class Method, class H>
void integrate(Method f, H h, const char * filename) {
  Vars v(1.0, 1.0);
  double t = 0;
  std::ofstream ofs(filename);
  std::cout << filename << std::endl;
  for (int i = 0; i < 200; i++) {
    t += dt;
    v = f(v);
    ofs << t << " ";
    ofs << v.x << " ";
    ofs << v.y << " ";
    ofs << h(v) << std::endl;
  }
}

手法Method fと、保存量H hを受け取って、それを呼んで出力するだけのルーチン。本格的に使うには初期条件や時間刻み、ループ回転数を渡せるようにするべきだが、ここではこれでいいことにする。やろうと思えばすぐできるし。

ついでにファイル名を受け取って、出力をそのファイルに保存するようにしてある。

結果

以上で全ての構成要素がそろった。メイン関数から以下のように呼び出せば良い。

  integrate(RungeKutta<LotkaVolterra::Diff>(dt), LotkaVolterra::H(), "lv_rk.dat");
  integrate(Euler<LotkaVolterra::Diff>(dt), LotkaVolterra::H(), "lv_euler.dat");
  integrate(RungeKutta<HarmonicOscillator::Diff>(dt), HarmonicOscillator::H(), "ho_rk.dat");
  integrate(Euler<HarmonicOscillator::Diff>(dt), HarmonicOscillator::H(), "ho_euler.dat");

いまいち美しくない気がするが、気にしないことにしよう。以下、時間刻みは$dt = 0.05$とし、初期条件$(x,y) = (1,1)$から200ステップの計算を行う。

調和振動子

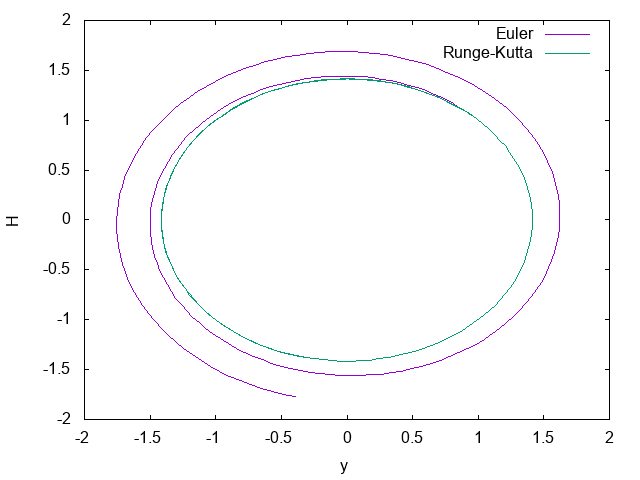
調和振動子の位相空間はこんな感じ。

harmonic-oscillator.png

Runge-Kuttaはちゃんと円になっているが、1次のEulerはどんどん半径が大きくなっている。

エネルギーの時間発展はこんな感じ。
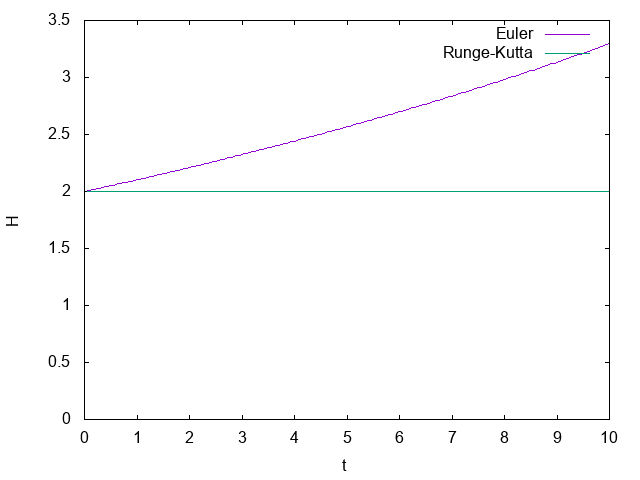
harmonic-oscillator-h.png

Runge-Kuttaではエネルギーがきちんと保存しているが、1次のEulerではどんどん増加してしまっている。

ロトカ・ヴォルテラ系

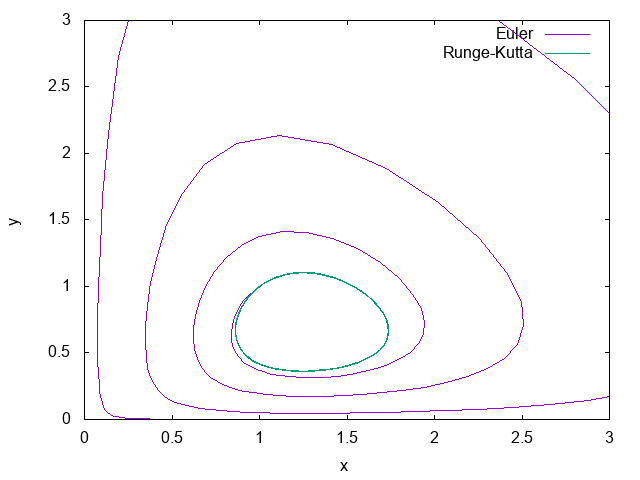
パラメータは$a = 2, b = 3, c= 4, d = 5$とした。位相空間はこんな感じ。

lotka-volterra.png

Runge-Kuttaでは保存量に対応した閉曲線を描いているが、1次のEulerではどんどん解が発散している。

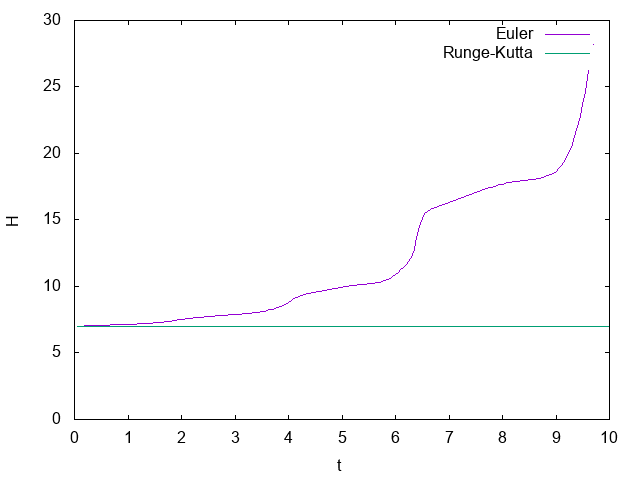
保存量の時間発展はこんな感じ。

lotka-volterra-h.png

Runge-Kuttaはちゃんと保存しているけど、1次のEulerはダメダメですね。

まとめ

微分方程式系と数値積分手法を自由に与えられるように関数オブジェクトで書いてみた。アセンブリ見てみたが、時間積分のループ内は全てインライン展開され、抽象化したことによる速度ペナルティは全く発生していない。例えばインテルコンパイラでは

$ icpc -O3 -S rk.cpp
$ c++filt < rk.s | grep call rk_f.s | grep -v std
        call      __intel_new_feature_proc_init                 #114.12
        call      log                                           #115.3
        call      log                                           #115.3
        call      log                                           #116.3
        call      log                                           #116.3
        call      _Unwind_Resume                                #118.3
        call      _Unwind_Resume                                #118.3
        call      _Unwind_Resume                                #118.3
        call      _Unwind_Resume                                #117.3
        call      _Unwind_Resume                                #117.3
        call      _Unwind_Resume                                #116.3
        call      _Unwind_Resume                                #116.3
        call      _Unwind_Resume                                #115.3
        call      _Unwind_Resume                                #115.3
        call      __intel_sse2_strlen                           #259.16

という感じで、余計な関数呼び出しがないことがわかる。過去の履歴が必要な多段法も同様に組めると思うけど、ベタ書きした場合に比べて速度ペナルティが無いように組めるかどうかまでは試してない。

  1. テンプレート慣れてないのでこういう書き方が一般的なのかは知らないが、最終的に全部インライン展開されたからいいんじゃない？ ↩

7
6
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
7
6