概要

シミュレーションなどではよく、微分方程式に従った時間発展を計算することがあります。そういった計算には、オイラー法やルンゲ・クッタ法と呼ばれるアルゴリズムを用いるのですが、自分でそうしたコードを記述するのは面倒だしバグの元でもあります。
boostには、そういった常微分方程式の数値解析用ライブラリ、boost::odeint が含まれています。できることを列記してみると、

用途に応じた幅広い常微分方程式計算用アルゴリズムが用意されており、簡単に切り替えも可能
自動で一定時間動かしたり、一ステップごとの処理を自分で書いたりと、目的に応じて幅広く使える
エラーに応じた最適なステップ幅の自動計算ができる（controlled_stepper）
ステップごとではなく、任意の位置における積分値の取得も可能（dense output stepper）
速度と位置を両方おいかけるような、ハミルトン力学系にも対応
単純な微分近似（陽解法）では解けない、繊細な系に対する解法（陰解法）も対応

本記事では、そんな優れもので便利な定微分方程式ソルバー boost::odeint の使い方について解説します。

まずは使い方

簡単な使用例

まず、簡単な例で使い方を見てみます。例えば、以下のような常微分方程式系を考えてみましょう。二つの変数、$x$, $y$ が互いに影響を及ぼしながら時間発展していきます。元ネタは、ロトカ＝ヴォルテラの方程式と呼ばれるものです。

\frac{dx}{dt} = x (\alpha -\beta y)

\frac{dy}{dt} = - y (\gamma - \delta x)

適当なパラメーターの元では、この系では$x$, $y$ が時間に対して振動することが知られています。これを、odeintを使って再現してみましょう。

odeintでこの常微分方程式を解かせるためには、state と system を定義してやる必要があります。

state は、変数 $x$, $y$ に当たる型です。自作クラスを使うこともできるのですが、ここでは簡単に標準コンテナstd::array<double,2>を使ってみます。

system は、微分方程式 $dx/dt$, $dy/dt$に相当する部分です。odeintでは、メンバ関数
void operator()(const state& x, state& dx, double t)
を持つ関数オブジェクトとして定義します。状態x、時間tを与えた時の微分値をdxに書き込んで戻してやります。

上記の微分系は以下のように書き表せられます。

struct lv_system {
public:
   using state = std::array<double, 2>;
public:
   double alpha;
   double beta;
   double gamma;
   double delta;
public:
   lv_system(double alpha_,double beta_,double gamma_,double delta_)
      :alpha(alpha_),beta(beta_),gamma(gamma_),delta(delta_){}

   void operator()(const state& x, state& dx, double t){
      dx[0] = x[0] * (alpha - beta* x[1]);
      dx[1] = - x[1] * (gamma - delta * x[0]);
   }
};

次に odeint に用意されている stepper とintegrate関数を選択します。

stepper とは、時間発展時に使用する常微分方程式計算用アルゴリズムが定義されたクラスのことです。odeintでは、state を引数に取るtemplateクラスとしてすでにいくつか用意されています。ここでは、オイラー法boost::odeint::euler<state>を使ってみましょう。

integrate関数とは、開始時間と終了時間を基に、stepperを使って実際に積分値を計算する関数です。observer(後述)と呼ばれる機能を使わない限り、integrate関数の違いはあまり意味がないので、とりあえずintegrate_const関数を使います。Stepper、Systemと、Stateの初期値、開始時間と終了時間、およびステップ幅を引数としてintegrate_const関数に入れれば、時間発展させた結果がState引数に書き込まれます。

int main(){
    lv_system System(2.0, 3.0, 4.0, 5.0);
    lv_system::state State = {1.0,0.5};

    std::cout << "time=0 " << "x=" << State[0] << " " << "y=" << State[1] << std::endl;

    //オイラー法を使ってみる
    boost::numeric::odeint::euler<lv_system::state> Stepper;

    //time = 0 -> 5まで、時間発展を計算してみる
    boost::numeric::odeint::integrate_const(
           Stepper, System, State, 0.0, 5.0, 0.05
        );

    std::cout << "time=5 " << "x=" << State[0] << " " << "y=" << State[1] << std::endl;
}

time=0 x=1 y=0.5
time=5 x=1.59949 y=0.780597

これで、$t$=5における$x$, $y$の値を計算することができました。

observerの使い方

ところで、多くの場合は時間発展した結果だけでなく、途中の軌道もほしいでしょう。そういった場合は、途中の時間$t$と状態$x$を記録するためのクラス、observerを用意してやります。メンバ関数として
void operator()(const state& x, double t);
を持っていること関数オブジェクトであれば、 observer として使うことができます。ここでは、時間と場所をcsvファイルに出力するobserverを用意してみます。

//csv形式で軌道を記録するobserver
struct csv_observer{
    using state = lv_system::state;
    std::ofstream fout;
    csv_observer(const std::string& FileName) :fout(FileName){};
    //ここで記録方法を定義する
    void operator()(const state& x, double t){
        fout << t << "," << x[0] << "," << x[1] << std::endl;
    }
};

observerを利用する際には、integrate_const関数の引数の末尾に追加してやるだけです。ただし、そのままだと値渡しになってしまいます。csvへの書き出しに使っているofstreamはコピーできないので、ここではstd::refを使って参照渡しにします。

int main(){
    lv_system System(2.0, 3.0, 4.0, 5.0);
    lv_system::state State = {1.0,0.5};

    std::cout << "time=0 " << "x=" << State[0] << " " << "y=" << State[1] << std::endl;

    //オイラー法を使ってみる
    boost::numeric::odeint::euler<lv_system::state> Stepper;

    //observerを用意する
    csv_observer Observer("result1.csv");

    //time = 0 -> 5まで、時間発展を計算してみる
    boost::numeric::odeint::integrate_const(
           Stepper, System, State, 0.0, 5.0, 0.05, std::ref(Observer)
        );

    std::cout << "time=10 " << "x=" << State[0] << " " << "y=" << State[1] << std::endl;
}

出力されたcsvファイルから結果を図示すると以下のようになりました。

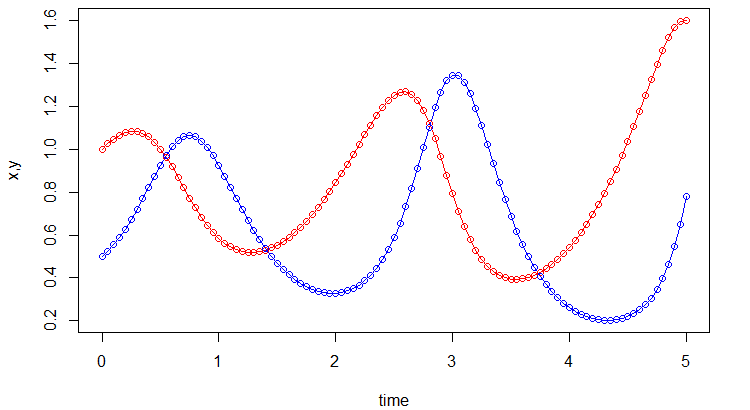
きちんと振動の軌跡が取れています。しかし、本来この系では振幅が一定のまま振動を続けるはずですが、計算結果では徐々に振幅が大きくなっています。これは、オイラー法の欠点で、特に振動するような系では推定精度が悪いことが知られています。

stepperを、より精度の良い4次のルンゲ・クッタ法に変えてみましょう。変え方は、Stepperを宣言している行を以下のように書き替えるだけです。

//オイラー法を使ってみる
//boost::numeric::odeint::euler<lv_system::state> Stepper;

//4次のルンゲクッタ法を使ってみる
boost::numeric::odeint::runge_kutta_4<lv_system::state> Stepper;

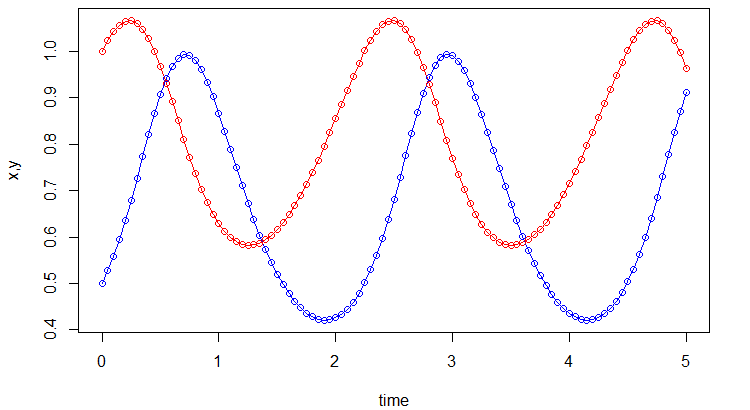
同じように出力されたcsvファイルから結果を見てみると、以下のようなきれいなグラフになり、正しく推定できていることが分かります。このように、必要に応じてアルゴリズムを簡単に切り替えられるのが、boost::odeintの特徴です。

controlled stepperを使う

odeintには、エラーに応じてステップ幅を自動的に調節してくれるstepper、controlled stepperがあります。利用する場合は、make_controlled関数にエラー推定可能なStepper（詳細は後述、Dormand-Prince 5法を使用）をtemplate引数に指定します。関数の第一、第二引数は、それぞれ絶対値、相対値の許容誤差です。

//オイラー法を使ってみる
//boost::numeric::odeint::euler<lv_system::state> Stepper;

//4次のルンゲクッタ法を使ってみる
//boost::numeric::odeint::runge_kutta_4<lv_system::state> Stepper;

//Dormand-Prince 5法による、Controlled Stepperを利用する
auto Stepper = boost::numeric::odeint::make_controlled<
   boost::numeric::odeint::runge_kutta_dopri5<lv_system::state>
>(0.0001,0.0001);

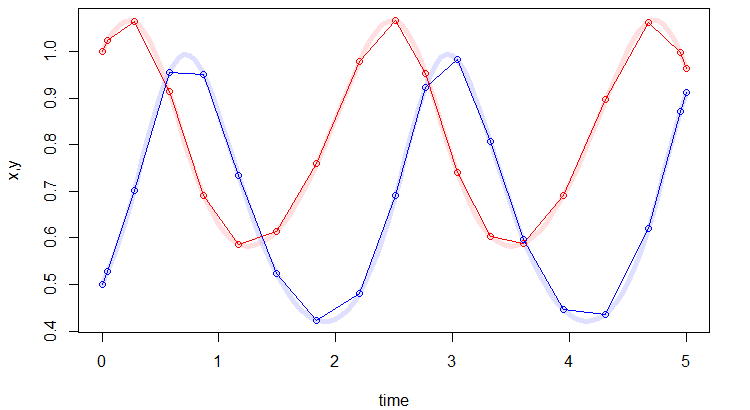
動かしてみると、以下のようなグラフになりました。上のグラフに比べるとステップ数（丸の数）が少なくなっているのが分かります。これは、指定されたエラー値を超えない範囲で、ステップ幅をステップごとに最適化しているためです。実際、ルンゲクッタ法の場合（薄青・薄赤線）と比べても推定値自体は見た目の上ではまったくずれていません。

さて、上記グラフを得るためには、Stepper以外にもう一か所、integrate関数を以下のように書き替える必要があります。

//boost::numeric::odeint::integrate_const(
//   Stepper, System, State, 0.0, 5.0, 0.05, std::ref(Observer)
//);

boost::numeric::odeint::integrate_adaptive(
   Stepper, System, State, 0.0, 5.0, 0.05, std::ref(Observer)
);

integrate_constがintegrate_adaptiveに変わっています。実は、integrate関数には複数の種類があり、それぞれobserverを呼び出すタイミングが違います。例えば、integarete_constは指定されたステップ幅で指定の時間幅ごとにobserverを呼び出すのに対し、integrate_adaptiveは毎ステップごとにobserverを呼び出します。このように、integrate関数をうまく使い分けることで、observerを呼び出すタイミングを自由に変えられるのです。

odeintの構造

ここまで、簡単にodeintの基本的な使い方を見てきました。見てのとおり、ユーザーは

系の変数を定義する "State"
微分方程式を定義する "System"
途中経過の記録方法を定義する "Observer"

の三つを用意してやるだけです。あとは、

ステップアルゴリズムを決める "Stepper"
observer呼び出し間隔を決める "integrate関数"

の二つをodeintから選ぶだけで、常微分方程式を解くことができる、素晴らしいライブラリとなっています。

以下では、これらodeintの機能や仕様について、もう少し詳しくみていきます。

stepperの選び方

odeintには、標準で多くのstepperが用意されています。どれを使うべきか迷ってしまいますが、以下の項目について考えることで、使うべきstepperを絞り込むことができます。

A. 利用したいstepperの機能。エラーに応じたステップ幅の自動調整や、任意の時間における状態取得が必要かどうか。

B. 対象とするsystem。odeintでは、通常の微分系Systemに加えて、ハミルトン力学系や陰解法と呼ばれる手法を使うために3つの特殊な系が定義されています。

C. その他、計算次数（いわゆるアルゴリズムの持つ精度）や内部情報の有無など。

A. stepperの機能からの分類

まず、stepperの機能についてみてみます。stepperには、持っている機能から大きく下記の3つのタイプに分けることができます。

指定されたステップ幅でstateを動かすStepper
エラーに応じてステップ幅を自動調整するControlled Stepper
ステップ幅の自動調整に加えてステップ間の任意のstateを計算できるDense Output Stepper

以下、各タイプのStepperが持つメンバ関数と、その使い方についてみていきます。

A.１通常のStepper

指定されたステップ幅でstateを動かす、最もシンプルなStepperです。メンバ関数として、
　　void do_step( const system& sys, state& x0, time& t0 ,time dt )
を持っており、$t$ = t0の時、$x$ = x0だったとしたときの、$t$ = t0 + dtの$x$の推定位置をx0に書き込んで返します。

A.2 Controlled Stepper

エラーに応じてステップ幅を自動調整するStepperです。メンバ関数として
　　boost::odeint::controlled_step_result try_step( system sys, state& x0,time& t0 ,time& dt)
を持っています。引数はdo_step関数と同じですが、この関数は以下の点が違います。

指定されたエラー値を超えた場合は、odeint::controlled_step_result::failを戻り値として返し、x0は変化させません。
次回推奨されるステップ幅をdtに書き込んで返します（戻り値がfailなら小さく、successなら（可能であれば）大きくなります）。
x0だけでなく、t0も書き変わります。

一部のStepperはそのままでControlled Stepperとして使えますが、多くの場合 make_controlled関数に基底のstepperを指定して作成することになります。第一、第二引数がそれぞれ絶対、相対許容誤差。第三引数が基底に指定するstepperです。

using base_stepper_type = boost::odeint::runge_kutta_dopri5<state>;
auto Stepper = make_controlled( 1.0e-10 , 1.0e-6 , base_stepper_type());

A.3 Dense Output Stepper

エラーに応じてステップ幅を自動調整するとともに、ステップ間の任意の時間$t$における状態$x$を取得可能なStepperです。メンバ関数として、
　　std::pair<double,double> do_step(system sys)
を持っています。戻り値のfirstが今回のステップの始まりの時間 $t_0$、secondが終わりの時間 $t_1$です。ユーザーは、境界を含む[$t0$,$t1$]の間の任意の位置のstateを、メンバ関数
　　void calc_state(double t, state& x)
を使って受け取ることができます（結果は第二引数に書き込まれます）。

現在の時間 $t_1$、状態 $x_1$、ステップ幅 $dt$は、それぞれ以下の関数で取得できます。
　　double current_time()
　　const state& current_state()
　　double current_time_step()

Controlled Stepper同様、多くの場合 make_dense_output関数に基底のstepperを指定して作成することになります。引数はmake_controlled関数と同じく、第一、第二引数がそれぞれ絶対、相対許容誤差、第三引数が基底に指定するstepperです。

using base_stepper_type = boost::odeint::runge_kutta_dopri5<state>;
auto Stepper = make_dense_output( 1.0e-10 , 1.0e-6 , base_stepper_type());

B. 対象とするsystem

odeintでは通常の微分系に加えて、3つの特殊な微分系をあわせた、計4種類のsystemがあります。

通常の微分系であるSystem
「位置と速度で加速度が決まる」ような二階微分が入っている系を扱うSecond Order System
いわゆるハミルトン力学系を扱うためのSimplectic System
陰解法を扱うためのImplicit System

stepperごとに対応しているsystemは決まっているので、利用したい微分系に対応したstepperを選ぶ必要があります。

以下では、それぞれのsystemの定義と、各systemにおいて利用できるStepperを順に見ていきます。

B.1 通常のSystem

以下のような微分系を持つ、一般的なシステムです。

\frac{dx}{dt} = f(x,t)

関数オブジェクトをsystemとして利用するためには、
　　void operator()(const state& x, state& dxdt, double t);
をメンバ関数に持っている必要があります。

odeintでは、通常のSystem用の多くの標準Stepperが用意されています。迷ったら、とりあえず以下の基準で決めるとよいでしょう。

どれにすべきか迷ったら、とりあえずControlled StepperにもDense Output Stepperにも使えるrunge_kutta_dopri5
固定長ステップでよければ、runge_kutta4
精度が必要なら次元の高いrunge_kutta_fehlberg78、特に高精度が必要なら任意の次元を指定できるbulirsch_stoer
system関数の計算量が大きい場合には、内部情報を持ちsystemの演算回数を最少にできるadams_bashforth_moulton

Algorithm	型名	次数	Controlled	Dense Output	内部情報
Explicit Euler	euler	1	☓	○	No
Modified Midpoint	modified_midpoint	configurable (2)	☓	☓	No
Runge-Kutta 4	runge_kutta4	4	☓	☓	No
Cash-Karp	runge_kutta_cash_karp54	5	△	☓	No
Dormand-Prince 5	runge_kutta_dopri5	5	△	△	Yes
Fehlberg 78	runge_kutta_fehlberg78	8	△	☓	No
Adams Bashforth	adams_bashforth	configurable	☓	☓	Yes
Adams Moulton	adams_moulton	configurable	☓	☓	Yes
Adams Bashforth Moulton	adams_bashforth_moulton	configurable	☓	☓	Yes
Bulirsch-Stoer	bulirsch_stoer	variable（high）	◯	☓	No
Bulirsch-Stoer Dense Output	bulirsch_stoer_dense_out	variable（high）	◯	◯	No

△：make_controlled関数やmake_dense_output関数を介して作成したクラスで利用可能
◯：クラスのメンバ関数としてtry_step関数やcalc_state関数を利用可能

B.2 速度・加速度を扱うSecond Order System

位置$x$と速度$v$で加速度$dv/dt$が決まるような系、つまり下記のような微分系の場合には、Second Order Systemを用います。

\frac{dv}{dt} = f(x,v,t)

関数オブジェクトをsecond order systemとして利用するためには、
　　void operator()(const state& x, const state& v, state& dadt, double t);
をメンバ関数に持っている必要があります。

なお、stepperやintegrate関数に利用する際には、stateをstd::pairとして渡す必要があります。

using state = std::array<double,3>;
struct second_order_system{
    void operator()(const state& x, const state& v, state& dadt, double t);
}
using second_order_state = std::pair<state,state>;

second_order_system System;
second_order_state State;
integrate_const(Stepper, System, State, 0.,10., 0.1);

上記例では、second_order_stateのfirstが位置$x$、secondが速度$v$となります。

Second Order System用に既定で用意されているアルゴリズムは、Velocity Verletのみです。内部情報を持っているため、利用する際は注意が必要です。

Algorithm	型名	次数	Controlled	Dense Output	内部情報
Velocity Verlet	velocity_verlet	1	☓	☓	Yes

B.3 ハミルトン力学系を扱うSymplectic System

Symplectic Systemは、以下のような微分系を持つ、いわゆるハミルトン力学系を扱うためのシステムです。

\frac{dx}{dt} = f(y)

\frac{dy}{dt} = g(x)

このような場合、systemは
　　void operator()(const state& x, state& dydt);
をメンバ関数に持っているオブジェクトのstd::pairとして定義します。なお、stateもstepperやintegrate関数に渡す場合には、std::pairにします。例えば、以下のような感じです。

using state = std::array<double,3>;
struct system_dx{
    void operator()(const state& y, state& dxdt);
}
struct system_dy{
    void operator()(const state& x, state& dydt);
};
using symplectic_state = std::pair<state,state>;
using symplectic_system = std::pair<system_dx,system_dy>;

symplectic_system System;
symplectic_state State;
integrate_const(Stepper, System, State, 0.,10., 0.1);

上記の例の場合、symplectic_stateのfirstとsecondがそれぞれ$x$と$y$、symplicit_systemのfirstとsecondがそれぞれ$dx/dt$と$dy/dt$となります。

なお、ハミルトン力学の特殊な場合として、微分系が以下のように書けることがあります。

\frac{dx}{dt} = f(y)

\frac{dy}{dt} = x

このような場合を特別にSimple Symplectic Systemと呼び、$dx/dt$に相当する関数オブジェクト/ポインタをstd::pairにすることなく直接stepperやintegrate関数に渡すことができます（stateは、std::pairにする必要があります）。

using state = std::array<double,3>;
struct system_dx{
    void operator()(const state& y, state& dxdt);
}
using simple_symplectic_state = system_dx;
using simple_symplectic_system = std::pair<system_dx,system_dy>;

simple_symplectic_system System;
simple_symplectic_state State;
integrate_const(Stepper, System, State, 0.,10., 0.1);

Symplectic System および Simple Symplectic System用のstepperは、下記の3つが用意されています。残念ながら、どのstepperもControlled StepperやDense Output Stepperには対応していません。

Algorithm	型名	次数	Controlled	Dense Output	内部情報
Symplectic Euler	symplectic_euler	1	☓	☓	No
Symplectic RKN McLachlan	symplectic_rkn_sb3a_mclachlan	4	☓	☓	No
Symplectic RKN McLachlan	symplectic_rkn_sb3a_m4_mclachlan	4	☓	☓	No

B.4 複雑系を扱うImplicit System

微分系が複雑な場合には、現在の状態のみから1ステップ先の状態を推定する陽解法ではなく、現在の状態と1ステップ先の状態の両方を同時に考慮する陰解法を用いた方が良い場合があります。陰解法を利用するためには、Systemを

状態$x$、時間$t$における微分係数を求めるvoid operator()(const state& x, state& dxdt, double t)をfirst
状態$x$、時間$t$におけるヤコビアンを求めるvoid operator()(const state& x, matrix& jacobi, double t)をsecond

とするような、std::pairの形で定義してやる必要があります。また、stateはboost::ublas::vectorを、ヤコビアンは、boost::ublas::matrixを、それぞれ利用する必要があります。

using state = boost::numeric::ublas::vector< double >;
using matrix = boost::numeric::ublas::matrix< double >;

struct system_state{
    void operator()( const state &x, state &dxdt, double t);
};
struct system_jacobi{
    void operator()( const state &x , matrix &J , const double &t );
};
using implicit_system = std::pair<system_state,system_jacobi>;
using implicit_state = state;

implicit_system System;
implicit_state State;
integrate_const(Stepper, System, State, 0.,10., 0.1);

当然ですが、stateが二つあるわけではないので、Symplectic Systemの場合と違ってstateをstd::pairにして利用する必要はありません。

Implicit Systemには、下記の二つのStepperがodeintには用意されています。精度が必要な場合は、必然的にrosenbrock4を使うことになります。rosenbrock4は、make_controlled関数やmake_dense_output関数を用いることで、Controlled StepperやDense Output Stepperとして利用可能です。

Algorithm	型名	次数	Controlled	Dense Output	内部情報
Implicit Euler	implicit_euler	1	☓	☓	No
Rosenbrock 4	rosenbrock4	4	△	△	No

△：make_controlled関数やmake_dense_output関数を介して作成したクラスで利用可能

C. 計算次数や内部情報の有無

上記の表で示した通り、Stepperの定義の違いとして、計算次数とともに内部情報の有無があります。

計算次数は大きいほど計算精度も当然上がりますが、一般にステップごとの計算量も増加します。オイラー法などの一次の次数しか持たないStepperは、「例示のためにのみ使用すべきである」として公式ドキュメントでも実用は避けるべき、との扱いとなっています。

内部情報を持つタイプのstepperは、内部で前回の計算結果を保持することで必要な計算量を節約しています。ただし、こうしたstepperは、下記のように複数のstateを一つのstepperで使いまわそうとしたときに問題になります。

boost::odeint::adams_bashforth_moulton<state> Stepper;
state State1;
state State2;

Stepper.do_step(System, State1, 0, 0.1);
//...Stepperを使った、State1を時間発展させる処理いろいろ

Stepper.do_step(System, State2, 0, 0.1);
//Error! StepperはすでにState1に基づいた内部情報を保持している

前回の呼び出し時と異なる値を持つStateに対してStepperを再利用するためには、initialize関数を呼び出す必要があります。

boost::odeint::adams_bashforth_moulton<state> Stepper;
state State1;
state State2;

Stepper.do_step(System, State1, 0, 0.1);

//Stepperに新たにState2に基づく内部情報を保持させる
Stepper.initialize(System, State2, 0, 0.1);

Stepper.do_step(System, State2, 0, 0.1);
//OK! 内部情報はState2に基づくものなので正しく動く

ただし、頻繁なinitializeは計算量の節約という利点を大きく減らすことになるので、同時並行で複数のstateを動かしたいときには、複数のstepperを使うか、内部情報を持たないstepperを使うようにすべきです。

stateとして使える型

odeintを使うためには、stateをユーザーが定義する必要があります。標準ではstd::array<double, N>やstd::vector<double>がstateとして利用可能です。また、boost::ublasが提供するベクトルクラスにも対応しています。

一方で、自分定義がしたクラスをstateとして扱いたい、という場合には、やや面倒ですがいくつかの定義を行うことで自作クラスも利用することもできます。詳しくは、記事末尾の付録を参照してください。

その他、C言語で作られたコンテナ様構造体等を、ラッパークラスを介して利用する方法などもありますが、詳細は省きます。詳しくは、boostの公式ドキュメントのState Typeに関する項目をご覧ください。

integrate関数とObserver

StepperとState、Systemさえあれば、時間発展を計算することはできますが、ある特定の時間までStepperで時間発展させる、といった処理を書くのはなかなか面倒です。odeintでは、時間発展させるためのヘルパー関数としてintegrate関数が用意されています。

integrate関数にはたくさん種類がありますが、基本的な違いはobserverを呼び出すタイミングです。

size_t integrate_const( stepper, system, x0, t0, t1, dt, [observer])

一定の時間間隔 dt でobserverを呼び出す。
t1を超えない限り、stepを回し続ける（t1になる保証はない）。
戻り値でstep数を返す。

Time integrate_n_steps( stepper, system, x0, t0, dt, n, [observer])

一定の時間間隔 dt でobserverを呼び出す。
t0 + dt*n となるまで、stepを回し続ける。
戻り値で終了時間を返す。

size_t integrate_adaptive( stepper, system, x0, t0, t1, dt, [observer])

毎ステップごとにobserverを呼び出す。
t1となるまで、stepを回し続ける（必ずt1で終わる）。
戻り値でstep数を返す。

size_t integrate_times( stepper, system, x0, t_begin, t_end, dt, observer)

時間配列のiteratorのペアを与えることで、任意の時間間隔でobserverを呼び出す。
戻り値でstep数を返す。

size_t integrate( system, x0, t0, t1, dt, [observer])

runge_kutta_dopri5を使うintergrate_adaptive。
戻り値でstep数を返す。

observer

integrate関数で時間発展の軌道を取得するには、observerクラスを利用します。odeintでは、下記要件を満たすクラスは、observerとして使用することができます。

void operator()(const state& x, double t);をメンバ関数に持つ

なお、integrate関数へは、すべてコピー渡しになります。内部に自前のコンテナやstreamクラスを持つ場合には、std::refを使って参照渡しを明示的に指定する必要があります。

Stepperによる違い

Stepper、Controlled Stepper、Dense Output Stepperのいずれもintegrate関数を利用することができますが、stepperのタイプによってやや動作に差があります。下記の点に注意して利用する必要があります。

Stepperの場合：integrate関数に指定されたdtが、ステップ幅になる。
Controlled Stepperの場合：dtは初期値として利用されるが、ステップ幅は最適化が行われる。ただし、observerの呼び出し時間間隔を超えないようにステップ幅は調整されるため、極端に短いobserverの呼び出し時間間隔を指定すると、Controlled Stepperのメリットが生かせない。
Dense Output Stepperの場合：dtは初期値として利用されるが、ステップ幅は最適化が行われる。Dense Output Stepperは任意の時間点のstateを取得可能なため、Controlled Stepperのようにobserverの呼び出し時間間隔によってステップ幅が影響を受けることはない。

おわりに

以上のように、boost::odeintは常微分方程式ソルバーとしては非常に汎用性に優れたライブラリです。常微分方程式という性質上、使いどころは非常に限られますが、シミュレーションなどのお供として一度使ってみてはどうでしょうか。

付録：自作クラスをstateにする

標準では、std::array<double, N>やstd::vector<double>は利用可能です。また、boost::ublasが提供するベクトルクラスにも対応しています。これらの標準で提供されているクラスをstateとして使いたくない場合、やや面倒ですが自作することもできます。自作する場合は、大きく二つの方法があります。

１．コンテナタイプのstateの自作

一つは、コンテナタイプのstateクラスを作成する場合です。要求されている要件は、

引数無しのデフォルトコンストラクタが用意されている。
iteratorを返すbegin/end関数が用意されている。
コンテナサイズに関する処理で、以下のどちらかが満たされている。
1. begin/endがランダムアクセスイテレータを提供しており、かつvoid resize(size_type)をメンバ関数として持っている。（正確にはコンテナクラスがboost::size(X)に対応し、かつX.resize(boost::size(X))が実行可能）
2. boost::numeric::odeint::same_size_imp<T,T>とboost::numeric::odeint::resize_imp<T,T>を特殊化している。
boost::numeric::odeint::is_resizeable<T>を特殊化している。

is_resizeableは、odeintが内部でresize処理を行うべきかどうか判定するためのものです。例えば、std::arrayのように、デフォルトコンストラクタで作成された時点ですでに要素が用意されている場合は、is_resizeableはfalseで特殊化します。一方、std::vectorのように要素が用意されておらず使用前にresizeによってメモリ確保が必要な場合は、is_resizeableはtrueで特殊化する必要があります。

ざっくりとまとめると、コンテナタイプの場合、下記のようなインターフェース & 定義をしてやる必要があります。

struct container_state{
    container_state();
    iterator begin();
    const_iterator begin() const;
    iterator end();
    const_iterator end() const;
    void resize( const size_t n ); //resize不要なタイプなら、処理は空でよい
};

namespace boost { namespace numeric { namespace odeint {
//iteratorがランダムアクセスイテレータの場合は不要
template< >
struct same_size_impl< state_type , state_type >{
    //v1とv2が同じsizeならtrueを返す
    static bool same_size( const state_type &v1, const state_type &v2 );
};

//iteratorがランダムアクセスイテレータ以外の場合は不要
template< >
struct resize_impl< state_type , state_type >{
    //v2と同じサイズにv1をresizeする
    static void resize( state_type &v1, const state_type &v2 );
};

//常に必要 resizeが必要かどうかに応じて定義
template< >
struct is_resizeable< container_state >{
    //resizeが必要な場合
    typedef boost::true_type type;
    static const bool value = type::value;
    //resizeが不要な場合
    //typedef boost::false_type type;
    //static const bool value = type::value;
};
} } }

２．ポイントタイプのstateの自作

もう一つは、例えばメンバ変数にx,yを持つようなポイントタイプのstateクラスを作成する場合です。

エラーコントロールが不要なStepper（後述）でしか使わない場合は、以下の要件を満たしているクラスなら、stateとして使えます。

state同士の加算 state_type& operator+=(state_type)及びstate_type operator+(state_type)が可能（boost::additive<state>に相当）
stateとdouble型の乗算 state_type& operator*=(double)及びstate_type operator*(double)が可能（boost::multiplicative<state, double>に相当）

エラーコントロールを利用したい場合、上記に加えてさらに以下の要件を満たす必要があります。

stateの要素ごとの除算 state_type operator/(state_type)が可能（boost::dividable1に相当）
stateの要素ごとの絶対値を戻す、state_type abs(const state_type&)が非メンバ関数として利用可能
stateの要素の絶対値の最大値を求めるクラス、boost::numeric::odeint::vector_space_norm_inf<T> を特殊化している。
- 例えば、二つのdouble型の要素 x、yを持つstateクラスの場合、std::max(std::abs(x),std::abs(y))に相当する処理です。

ざっくりとまとめると、下記のようなインターフェース & 定義をしてやる必要があります。

struct point_state{
    point_state();
    point_state& operator+=(const point_state&);
    friend point_state operator+(const point_state& p1, const point_state& p2);
    point_state& operator*=(double);
    friend point_state operator*(const point_state& p, double val);
    //エラーコントロールが必要な場合のみ
    friend point_state operator/(const point_state& p1, const point_state& p2);
};

//エラーコントロールが必要な場合のみ
point_state abs(const point_state&);

//エラーコントロールが必要な場合のみ
template<>
struct vector_space_norm_inf< point_state >{
    typedef double result_type;
    double operator()( const point_state &p ) const;
};

C++で常微分方程式：boost::odeint入門

概要