はじめに

Twitterで見かけた「一見平等に見えるルールが不平等を生む」という話題についてのちょっとした覚書です。

ゲームのルール

こんな「ゲーム」を考えます。

最初、6人がリンゴを一つずつ持っている
6人はそれぞれ1〜6までの番号が振られている
サイコロを二回振り、最初に出た目の人が、次に出た目の人にリンゴを一つあげる。ただし、最初の人がリンゴを持っていない場合はそのまま
以上を繰り返す

この試行を繰り返した時、リンゴを持っている数の分布はどうなるでしょうか？

ウェブで定期的に話題になるためご存知の方も多いでしょうが、十分時間がたつと多くの人がリンゴを一つも持たず、リンゴが一部の人に偏る「富の独占」がおきます。この「ゲーム」は、

公平なルールであっても富の独占は起きる
このゲームにおいて富を独占する人はたまたま運が良かっただけであり、特に他の人よりも優れていたわけではない

といった文脈で語られることが多いようです。

ですが、「なぜ富の独占が起きるのか」という議論はウェブではあまり見かけません(参考文献に挙げた書籍には書いてあるようです)。

というわけで、この「ゲーム」の背後にある数理にちょっとだけ触れてみます。

シミュレーション

まずは「富の独占」を再現してみましょう。Rubyではこんな感じになるでしょうか。

test.rb

S = 6
N = 1000000
a = Array.new(S){1}
d = Array.new(S+1){0}

r = Random.new(1)

N.times do |i|
  k1 = r.rand(S)
  k2 = r.rand(S)
  if a[k1] !=0
    a[k1] = a[k1] - 1
    a[k2] = a[k2] + 1
  end
  a.each do |n|
    d[n] = d[n] + 1
  end
end

d.each_with_index{|v,i|
  puts "#{i} #{v.to_f/N}"
}

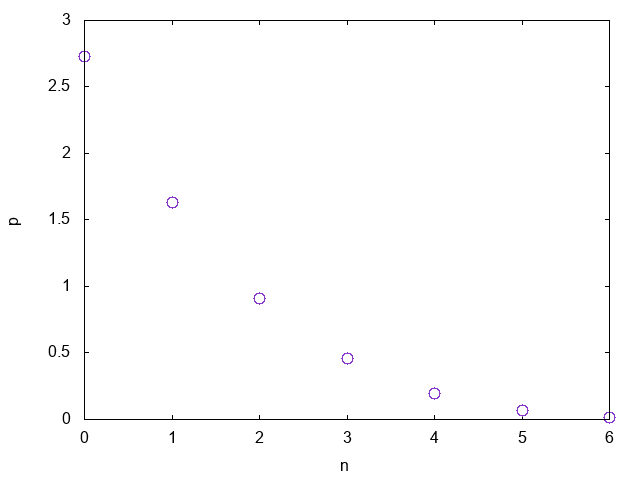
Sが人数、Nが試行回数です。実行結果はこんな感じになります。

$ ruby test.rb
0 2.729575
1 1.634563
2 0.907818
3 0.455346
4 0.193464
5 0.065497
6 0.013737

グラフにするとこんな感じ。

もともと6人が一つずつリンゴを持っていたのに、リンゴを持っていない人が2.7人、一つだけ持っている人が1.6人となりました。つまり、国民の73%が、平均以下の資産を持つことになります。これが「富の独占」とか「貧富の差」とか言われているものです。

数理的な背景

さて、経済学的なプロパガンダはともかくとして、何が起きているか考えてみましょう。この問題は、例えば固定境界のあるランダムウォークとして定式化できますが、私がナイーブに遷移確率を書き下そうとしたら非線形の項が出てきてしまってうまく解けませんでした¹。

そこで、統計力学で出てくる「等重率の仮定」を置きましょう。つまり、全ての微視的状態は全て同じ確率で実現する、というものです。すると、この問題は「リンゴの数」をエネルギーとみなし、お互いにエネルギーを自由にやり取りする多数の粒子の問題と等価になります。

リンゴの数がエネルギーですから、この系のハミルトニアン$H$は、リンゴの数を$n$とすると$H(n) = n$です。全リンゴの数及び全粒子の数を$N$とすると、この系の平衡状態$f_k$は、以下のエントロピー

S = \sum_{k=0}^{N} f_k \log f_k

を、全粒子の数が$N$である条件

N = \sum_{k=0}^{N} f_k

及び、全リンゴの数が$N$である条件

N = \sum_{k=0}^{N} k f_k

のもとで最大化した状態として実現されます。

ここで$n$について連続化して、変数を$x$としましょう。分布関数$f(x)$は、リンゴを$x$個持つ人の数です²。

ラグランジュの未定定数法により、

F = \int( \beta x f - f \ln f + \lambda f) dx

の変分を取ると、求める分布は

f(x) = Z^{-1} \exp(-\beta x)

となります³。ただし、$Z$や$\beta$は全粒子の数や全エネルギーについての条件

\begin{align}
N &= \int f dx \\ 
N &= \int x f dx 
\end{align}

から決まります。本当は積分範囲は0から$N$までですが、どうせ$x$が大きいところでは被積分関数が小さくなるので積分の上限を無限大に近似してしまいましょう。そうすると、$Z=1/N$、$\beta =1$と決まります。以上から、分布関数は

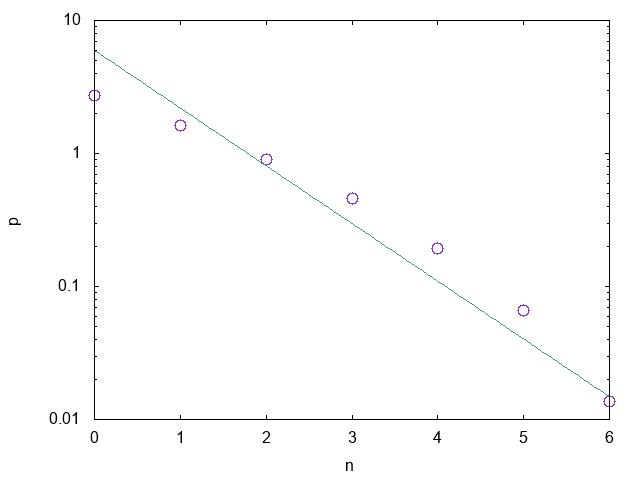
f(x) = N \exp(-x)

と求めることができました。先程得られた結果と比較してみましょう。縦軸を対数スケールにとってあります。

連続近似や、$N$が大きいという近似を入れたのでちょっとずれてしまいますが、まぁまぁ合っていますね。

まとめ

サイコロゲームによる「貧富の差」が出てくる問題を、統計力学の問題として解いてみました。この「富の分布」は、富に比例するハミルトニアンを持つ系におけるボルツマン分布にほかならないことがわかります。

この系における「等重率の仮定」の妥当性の説明を考えたのですが、わかりやすい説明を思いつきませんでした。気になった人は身近にいる熱・統計力学の専門家に聞いてみてください。もし良い説明をお持ちの方はコメント欄等でお知らせいただけると幸いです。

最後まで書いて思いましたが、参加人数とリンゴの数を同じにしたのは、問題設定的にあまりよくなかったかもしれませんね。

この話が面白いと思った人はコーヒー豆の数理も好きかもしれません。

参考文献

[データの見えざる手: ウエアラブルセンサが明かす人間・組織・社会の法則]矢野和男(著)(https://www.amazon.co.jp/dp/4794220685/)

私はまだ読んでいないのですが、上記の本にこのサイコロゲームの結果がボルツマン分布になる説明が記載されているようです。

追記

tsekineさんより、

取りうるのは
6/0x5
5/1/0x4
4/2/0x4, 4/1x2/0x3
3x2/0x4, 3/2/1/0x3, 3/1x3/0x2
2x3/0x3, 2x2/1x2/0x2, 2x1/1x4/0
1x6
の11状態かと。11x11 の行列をあれこれすると、解析的に解ける気がします。 https://t.co/n6iOHMPGpG
— Tatsuo Sekine (@tsekine) 2018年1月11日

という指摘がありました。確かにこれならできそうな気がします。後で試してみます。

追記(2018年1月13日)

上記の状態でマルコフ遷移行列を書いて基底状態を厳密に求めました。詳しくは次の記事続・サイコロゲームと貧富の差をどうぞ。

この問題をマルコフ過程として解析的に解く方法をご存知の方がいたらお知らせください。 ↩
連続化しているので、もうちょっと厳密に言えば持っているリンゴの数が$x$から$x+dx$の間にある人の数が$f(x)dx$ということです。 ↩
ここで$Z = \exp(-1 -\lambda)$で、これは分配関数と呼ばれるものです。 ↩