はじめに
だいぶ前だが、職場でコーヒーミルが話題になった。コーヒー豆を挽いた時、粒が揃っているほうが良い、というのはよく聞く話だが、実際の豆のサイズ分布はどうなってるんだろう?ちゃんとある平均サイズの周りにガウス分布しているんだろうか? プロペラ式はよくないと言われるが、実際にどうなんだろう?
というわけで、理想的な条件で考えてみる。
近似
プロペラ式のコーヒーミルを理想化して考える。簡単のため、以下のような理想的な条件を考える。
- 豆を一次元とする
- 豆の大きさ(長さ)に比例してカッターがぶつかる豆が選ばれる
- カッターが豆にあたったら、その場所でスパッと二つに切れる
- カッターが豆にあたる場所は一様分布とする
相当、荒っぽい近似だが、この作業を続けていった時に、豆はどのようなサイズ分布になるか、という問題である。ここまで見た瞬間に答えが分かった人は、この先を読む必要は全くない。それ以上の情報は今後出てこないから。
数値計算
問題を見た瞬間に分布が思い浮かばなかった人(俺)は、数値計算することにしよう。ナイーブに実装するなら、
- (0,1)の線分を用意する
- 乱数により、線分の一箇所をランダムに選ぶ
- その場所を二つに切る
- 乱数で切る線分を長さに比例して選び、選ばれた線分の位置をランダムに選ぶ
- その場所を二つに切る
という処理を繰り返せばよろしい。しかし、この方法は無駄である。線分を長さに比例して選び、そこを切る、というプロセスは、わざわざ線分を選ぶ必要は無い。ただ(0,1)の乱数を発生させて、その場所をぶった切れば、長さに比例して線分を選んでさらにその線分を切ることと等価である。
従って、
- (0,1)の線分を用意する
- ひたすら乱数を発生させて線分をぶった切る
- 線分の長さ分布が求める分布
と問題が簡略化された。ここまで見た瞬間に答えが分かった人は、この先を読む必要は全くない。それ以上の(略
スクリプト
というわけでスクリプトを書いてみよう。分布を見る時には生分布ではなく累積分布関数を使うのが便利である。結局、上記の分布はソート二回で求めることができる。
a = Array.new(1000) do
rand
end
a.sort!
b = Array.new(a.size-1) do |i|
a[i+1] - a[i]
end
b.sort!
s = b.size
s.times do |i|
puts "#{b[i]} #{i.to_f/s}"
end
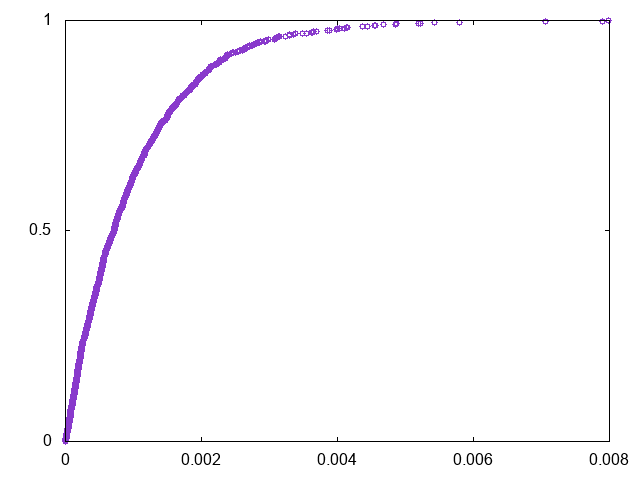
この実行結果、すなわちコーヒー豆のサイズの累積分布関数はこうなる。
さすがにこれみて気がついた。ランダムにイベントを発生させた時のイベント間の時間の分布だから、これは指数分布ですね。
まとめ
カッターが豆のサイズに比例してランダムにぶちあたり、あたった豆はスパっと二つに切れる理想的なプロペラ式のコーヒーミルを考えた。その結果、非常に細かい豆多数と、大きな豆が少数という、コーヒーをいれるには最悪のサイズ分布となった1。すなわち、理想的なプロペラ式コーヒーミルでは理想的なコーヒーをいれることはできない(ドヤ)。
-
もともと計算の動機は、職場の人が「プロペラ式だとうまく粒径が揃わない気がする」と言ったのを確認するためだったので、この人の直感は正しかったことがわかった。 ↩