はじめに
前回、三目並べの全探索をやってみました。今回は得られた評価関数を特異値分解という手法で圧縮、近似してみる話です。
コードはここに置いてあります。
評価関数について
そもそもゲームのAIにおける評価関数とはなんでしょうか?とりあえずここでは囲碁や三目並べのようなゲームのAIに話を限定し、「現在の状態が与えられた時、盤面のどこに置いたらどれだけ有利かを与える関数」と定義してみましょう。
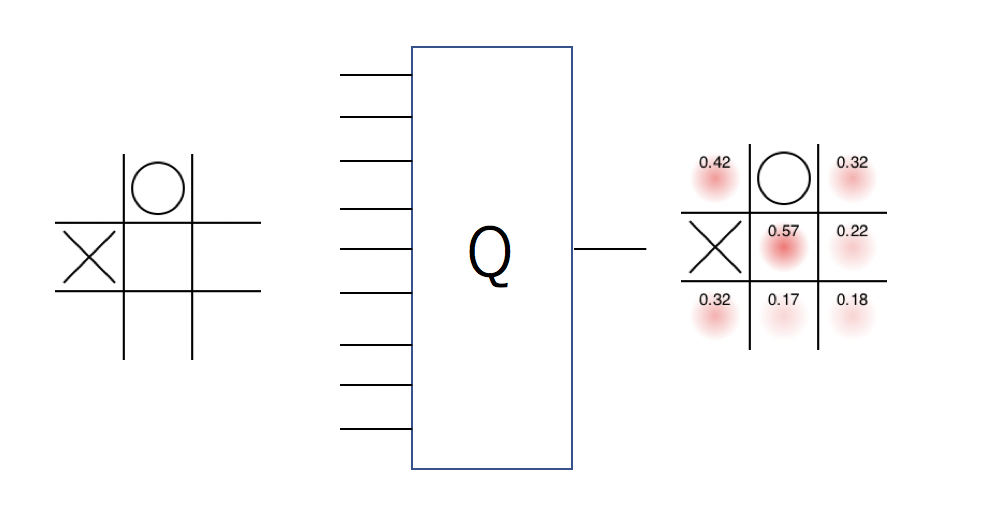
例えば三目並べなら、左の局面を与えられたら、右図のような「それぞれの手における勝利確率」が返ってくるような関数が欲しくなります。

さて、この評価関数の入力は盤面の状態です。三目並べなら、各マスが三通りの状態を取ることができ、それが9マスあるため、対称性その他を考えなければ$3^9 = 19683$通りの入力があります。出力は、「9マスのうちどこに置くとどれだけ有利か」のため、9次元のベクトルで表現できます。
従って、この評価関数は、以下のような10次元配列で表現されることがわかります。
double Q[3][3][3][3][3][3][3][3][3][9];
この配列の最初の9次元は状態の入力、最後の1次元は出力を表します。何もないところを0、先手(○)を1、後手(X)を2とすると、先程の図なら入力は(0,1,0,2,0,0,0,0,0)です。この状態において、例えば一番左上に置いた時の評価値は
Q[0][1][0][2][0][0][0][0][0] = 0.42;
ということになります。
つまり、「すべての状態を尽くすことができるならば」評価値とは単なる配列であり、ゲームAIは単に状態と評価値を丸暗記すれば良いことになります。もちろん、実際にはこんな配列は作ることができないため、「ゲームの取り得る状態」よりも極めて少ない情報量で、ゲームの評価値を表現しなければなりません。そのためにニューラルネットワークなりなんなりを用意し、それを「鍛える」ことで思考ルーチンを作ろうとするわけです。
しかし、せっかく三目並べにおいては、普通は求まることがない「評価関数の配列表現」が得られているので、逆に厳密な評価関数の配列表現を近似することで思考ルーチンを作ってみましょう。
つまり、通常とは逆に、まずは神様のような脳みそを作っておき、それを「容量の少ないHDD」に収めるために情報を圧縮します。この圧縮具合によって、どれだけ「アホになるか」を見てみましょう、というのが本稿の目的です.

テンソルと特異値分解について
注:テンソルについてよく知っている人はこの節は飛ばして構いません。
みなさんの「テンソル」との出会いはいつでしょうか?大学の電磁気学か、力学などで出てくる応力テンソルあたりが「テンソルとの出会い」なんじゃないかと思います。その時、「あぁ、行列の素直な拡張だな」と思ってすぐに飲み込めた人は幸運というか、(少なくとも僕より)センスがある方だと思います。残念ながら僕は当時テンソルがまったく理解できず、非常に苦労しました。
ここではテンソルと、テンソルの特異値分解について簡単におさらいしてみます。
テンソルの図形表現
そもそもベクトルや行列とはなんだったでしょうか?いまのカリキュラムは知りませんが、おそらくベクトルが出てくるのは空間図形などで、行列は連立方程式を解くためか、回転を表す表現であるみたいに習ったことかと思います。
ここではそれをまるっと忘れて、プログラマ的に考えてみます1。
ベクトルとは、一次元の配列のことです。
double vector[D];
ここでDはベクトルの次元です。ベクトルは「0からD-1までの数字をいれると、一つ値を返してくれる離散的な関数」だと思うことができます。単なるデータベースだと思っても構いません。
同様に、行列は二次元配列のことです。
double matrix[M][N];
これもベクトルと同様に、二組の数字を入力したら、一つ値が返ってくるデータベースだと思えばいいです。次元はそれぞれMとNです。対応するカッコを「足」と呼びましょう。ベクトルは一本足、行列は二本足です。次元は「足の太さ」を表します。
後のために、図で表現します。

人や状況によって丸や三角、四角で表したりしますが、とりあえずなんか二次元図形はベクトルや行列、線が「足」です。一本足ならベクトル、二本足なら行列です。
さて、全く同様にしてテンソルを考えることができます。
double tensor[D1][D2][D3];
例えば、三次元配列で三階のテンソルを表現できます。テンソルの「足」の数を「階」と表現します。ベクトルは一階のテンソル、行列は二階のテンソルです。配列では「次元」は足の数を表現していますが、ここでは「次元」を足の太さの意味で使うので注意してください。上記の例では、tensorは「三階のテンソルで、それぞれの足の次元がD1、D2、D3」となります。
ただ、本稿では今後、「三階のテンソル」とは言わずに、単に「三本足のテンソル」と呼ぶことにします。
テンソルの図形表現を導入しました。この図形表現で重要なのは「線を結んだら、その足について和を取る」という約束です。
例えば行列にベクトルをかけるとベクトルになりました。
$$
y_i = \sum_j A_{ij} x_j
$$
これを図で表現するとこうなります。

右で、線がつながったため、「外に出ている足」は一本になったため、全体として足が一本、つまりベクトルになったと思えば良いです。
テンソルも同様です。以下は、4本足のテンソルと3本足のテンソルの、一つの足をつぶして、全体として5本足のテンソルができたところです。

実際には複数本の足を同時につぶすこともできますが、本稿では扱いません。
特異値分解
行列は、特異値分解(Singular Value Decomposition)という分解ができます。
ある行列$M$が$m$行$n$列の行列とする時、この行列は以下のように分解できます。
$$
M = U S V
$$
ただし、$U$は$m$行$m$列の正方行列、$S$は対角行列、$V$は$n$行$n$列の正方行列です。通常$V$は$V^*$のように随伴行列として書きますが、ここでは単に$V$として書くことにします。
この分解の何が嬉しいかですが、まず$S$の要素はかならず実にとれ、この要素を特異値と呼びます。そして特異値を大きい順に並べること約束すると、$U$や$V$が、ベクトルを「重要な順」に並べたものになります。

ここで$U$は列ベクトルが左から順番に、$V$は行ベクトルが上から順番に並びます。ここで「重要度」というのは、途中で打ち切った時に、もとの行列を再現するのにどれだけ重要か、という意味です。
$m$行$n$列の行列と、$n$行$k$列の行列の積は、$m$行$k$列になるのでした。この時、大きさによっては、かける行列の要素数よりもかけた結果出てくる行列の要素数の方が多くなるときがあります。
例えば5行1列の縦ベクトルと1行5列の横ベクトルをかけると、5行5列の行列ができます。もともと10個の要素しかなかったのに、25個の要素の行列を作ることができました。
このように、より小さな行列二つをかけることで、大きな行列を「再現」することができます。その「最適な小さな行列の作り方」を与えるのがSVDです。
さて、行列$M$を二つの行列の積に分解するのですが、真ん中に対角行列$S$がありますね。これをどうするかはいろいろ流儀があるのですが、ここでは$S$の平方根を左右それぞれに分けてかけてあげることにしましょう。

例えば$d$で近似する場合には、$L$の左から$d$個の列ベクトルを、$R$の上から$d$個の行ベクトルを取ったものを使います。
さて、テンソルをSVDしたい時には、足をまとめて行列にして、それからSVDします。下の図は5本足のテンソルをSVDした例です。

この例では、5本足のテンソル$T$を、左に足3本、右に足2本をまとめてSVDしました。SVDをすると、二つにパキっと割れて、真ん中が線で結ばれます。この例では、5本足のテンソル$T$が、4本足のテンソル$L$と、3本足のテンソル$R$に別れました。
新たに現れた真ん中の線は、二つのテンソルの間の「情報」を伝達する役割を果たしています。全部の情報を渡していれば、二つのテンソルの積は$T$に一致しますが、この線を「細く」することで近似を入れます。二つのテンソルが独立していればいるほど、細い線でよく近似できることになりますが、二つのテンソルが強く相関していると線をあまり細くできません。
三目並べの特異値分解
さて、準備が済んだところでいよいよ三目並べの評価関数の特異値分解をしましょう。
冒頭で述べたように、三目並べの評価関数は10次元の配列で表現できます。
double Q[3][3][3][3][3][3][3][3][3][9];
これは、10本足のテンソルだと思うことができます。
各マスにつながった9本の足から状態を入力し、9次元のベクトルを出力するテンソルです2。
このベクトルを、こんな感じに分解してみましょう。

10本足のテンソル$Q$が、4本足のテンソル$L$、5本足のテンソル$C$、4本足のテンソル$R$に分解されました。これは、もとの三目並べでいえば、縦につながっているところでパキっと割ったことに対応します。本当は、三目並べのルールに対応して、縦、横、斜めがつながるような分解をしたかったのですが、それだとループが出てきてしまい、SVDが使えなくなるそうので3、とりあえずただパキっと割ってみました。
以下、この「割り方」を説明します。僕の第一言語はRubyですが、こういうことをやるのはやっぱりPythonが強いので、Pythonでやります。
まず、予めRubyで評価関数Qの配列表現を求めておき、バイナリファイルに落としておきます。
File.binwrite("data.dat", Q.pack("d*"))
これをPythonで読み込みます。
from scipy import linalg
import numpy as np
A = np.fromfile("data.dat", dtype="float64")
これで$A$には、177147次元のベクトルとしてデータが読み込まれました。これを二つにわるために、足二本の行列に変形します。
B = A.reshape((27, 6561))

そしてこれをSVDします。これは、Qの足3本と残りをわけたことに対応します。

次に$CR$を$C$と$R$に割りたいわけですが、出力の足が一番右にあるため、このままではうまく割れません。そこで足の入れ替えをします。
今、$CR$の足は、入力の足を「I」、出力の足を「O」として、「IIIIIIO」と並んでいます。これを「IIIOIII」と並び替えたいわけです。そのためにはreshapeとtransposeを使います4。
CR = CR.reshape((d, 27, 27, 9))
CR = CR.transpose([0, 1, 3, 2])
CR = CR.reshape((d*27*9, 27))
足を入れ替えたので、$CR$をまたSVDします。

これで元のバカでかいテンソル$Q$を、3つのテンソルの和で書くことができました。

新たにあらわれた赤い足が、近似に使うボンドです(よく、virtual bondと呼ばれます)。この足の次元$d$を27にとると、全ての情報を伝えることができるために$Q$に一致します。$d$を27から減らしていくと、$Q$を近似したことになります。
さて、どのくらい近似できるか考えてみましょう。もともと$Q$は足が10本あり、9本の次元が3、1本が9なので、テンソルとしての要素数は177147個です。
対して、$L$と$R$の要素数は$27d$、$C$の要素数は$243 d^2$あります。
例えば$d=13$とすると、要素数は41769、およそ1/4になり、情報が圧縮できたことになります。
結果
というわけで結果を見てみましょう。
もともとSVDは、「もとの行列のフロベニウスノルムの差を最小にするための最良近似」であることが知られています。なので、$d$を27から減らしていって、元のテンソルとの差のフロベニウスノルムがどうなるか見てみましょう。
もとのテンソルを$Q$、近似されたテンソルを$Q' = LCR$として、
$$
r = \frac{|Q-Q'|}{|Q|}
$$
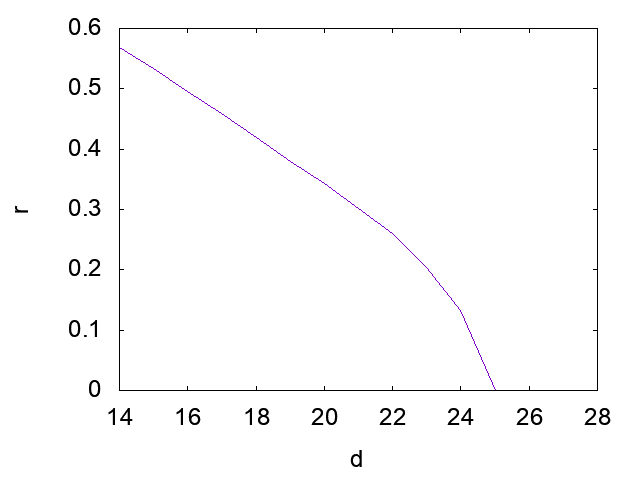
を$d$の関数としてプロットしてみましょう。
$d$が大きいうちは良いですが、$d$を下げていくと急速に近似が悪くなります。フロベニウスノルムの相対誤差を見ているので、誤差は最大でも$1$です。従って、$0.5$というのは非常に近似が悪いことを意味します。
あまり期待できそうにありませんが、$d=14$の時の近似された評価関数を見てみましょう。

かろうじて
- 真ん中を重視する
- 端より角を重視する
という性質は保っていますが、かなり数字がぶれてしまいました。
実は$Q$を$L$と$CR$に分けた時に、特異値がダラダラと下がっていたことから、途中で打ち切ると近似が悪いことはわかっていました。特異値分解による近似がうまくいくのは、特異値が指数関数的に落ちる時で、「だらだらと落ちる」時にはうまくいかないことがわかっています。
まとめ
三目並べの厳密な評価関数をテンソルだと思ってSVDし、その近似してみました。テンソルをSVDでパキっと割ってみた時、両側のテンソルの「情報」を伝える足(virtual bond)が意外に重要で、あまりうまく近似ができませんでした。
実は他の格子模型などでも、相転移点など「面白そうなところ」は特異値がダラダラと落ちて、SVDが良い近似を与えないことが知られています。SVDとは要するに空間を左右に分けた時の「つながり具合」を示すものなので、ゲームでも物理模型でも、「面白いところ」はうまく分けられない、ということを意味しているのかもしれません。
三目並べで言えば、本来は縦、横、斜めにつながっているべき空間を無理やり縦に分けてしまったのが敗因な気がします。例えば

みたいなテンソルネットワークを組めばよさそうな気もするのですが、ループがあるためにSVDが使えません。また、これでは斜め線が入っていませんね。斜め線もいれると次元が大きくなりすぎてあまり圧縮できる気がしません。おそらくテンソルネットワークではなく、他のネットワークの方が良い気がします。ですが、そもそも三目並べは状態数が少ないため、ちょっと複雑なネットワークを持ってくると状態を「丸暗記」できてしまうため、ちゃんと学習できているかの確認が難しそうですね。