はじめに
Step 2では、ペアリストの導入とBookkeeping法を実装した。しかし、ペアリストの作成はO(N^2)だったので、これをメッシュ探索でO(N)に落とす。
今回のコードはgithub/kaityo256/mdstep/step3においてあるので、適宜参照されたい。
- その1 $O(N^2)$のルーチンまで
- その2 ペアリストの構築とBookkeeping法
- その3 メッシュ探索 ← イマココ
- その4 少しだけ高速化
- その5 温度制御法を三種類実装してみる
- その6 圧力測定ルーチンの実装
メッシュ探索
要するに世の中を碁盤の目状(メッシュ)に切って、それぞれに通し番号を振る。そして原子がどの番地にいるかを住所録に登録してから、「12番地にいる人と相互作用する可能性がある人が住んでいるのは11番地、12番地、13番地に限られる(一次元の場合)」という状況を利用して住所から逆引きして相互作用相手を探しにいくスキームである。
言葉にすると簡単だが、意外にコードを組むのは面倒くさい。やるべきことは大きく分けて二つ。
- 住所録の作成
- 住所録にもとづいた探索
以下、それぞれについて説明する。なお、そこそこコード量があるため、メッシュ情報を保持するMeshListクラスを作ることにしよう。ファイルはmeshlist.cppとmeshlist.hppとする。
住所録の作成
まず、どの原子がどの番地にいるか、住所録を作らなければならない。住所録というが、実質的にやることは番地番号による原子インデックスのソートである。まず、区画の大きさを決める。探索の都合から、相互作用相手は隣接番地にのみ存在するようにしたい。つまり、隣の隣の番地には相互作用相手はいない。より正確には、ペアリストに登録すべき相手はいない。そのためには、一つのブロックの大きさが、カットオフ+マージンよりも長くないといけない。特に、「ぴったり同じ」になっている時には低確率でバグるので注意が必要である。
そのためには、まず「一辺のメッシュの数」を、ピッタリサイズより1小さくしておけば良い。
const double SL = CUTOFF+MARGIN;
m = static_cast<int>(L/SL) - 1;
mesh_size = static_cast<double>(L)/m;
SLが探索長さ(カットオフ+マージン)で、それでシステムサイズLを割ればメッシュの数となるが、例えばL=10で、SL=2.5だとちょうど割りきれてしまい、mesh_sizeが探索長さぴったりになってしまう。その場合は「ちょうど領域の端ピッタリ」に原子がいるとバグることがある。そこで、系を覆うメッシュがちょっと系をはみ出すようにするため、1引いておく。
後で気がついたが、一辺のメッシュの数が2よりも小さいとバグる。例えばメッシュの数が2だと右と左のブロックが同じものになってしまう。そこで、
assert(m > 2);
assert(mesh_size > SL);
とassertを入れておこう。
次に、住所録を表現するための領域を作る。具体的には以下の配列を作る。
- std::vector count; // どの番地に何個原子がいるかの数
- std::vector indexes; // 番地番号でソートした際に、番地番号の頭出しのインデックス
- std::vector sorted_buffer; //番地番号でソートした原子インデックス
最終的に作りたいのは番地番号でソートした原子インデックス、sorted_bufferである。そのために2パスソートを行う。
まず最初に、どの番地に何個の原子がいるかをカウントする。これはO(N)の手間でできる。
Atom *atoms = vars->atoms.data();
const int pn = vars->number_of_atoms();
std::vector<int> particle_position(pn);
std::vector<int> pointer(number_of_mesh);
std::fill(particle_position.begin(),particle_position.end(),0);
std::fill(count.begin(),count.end(),0);
std::fill(pointer.begin(),pointer.end(),0);
double im = 1.0/mesh_size;
for(int i=0;i<pn;i++){
int ix = static_cast<int>(atoms[i].qx * im);
int iy = static_cast<int>(atoms[i].qy * im);
int iz = static_cast<int>(atoms[i].qz * im);
// 周期境界条件補正を省略
int index = ix + iy*m + iz *m*m;
assert(index >=0);
assert(index < number_of_mesh);
count[index]++;
particle_position[i] = index;
}
具体的にはMeshList::make_pairのこの部分である。それぞれの原子について、番地番号(index)を計算し、その番地の住人の数(count[index])を増やしている。また、自分の番地番号をparticle_position[i]にキャッシュしている。
次に、原子を番地番号でソートしたときに、ある番地の始まりがどこにくるかのインデックスを作る。これは部分和を取ればよい。
indexes[0] = 0;
int sum = 0;
for(int i=0;i<number_of_mesh-1;i++){
sum += count[i];
indexes[i+1] = sum;
}
以上の準備のもとに住所録を作る。indexesが、「n番地の住人がはいる一番最初の場所」であり、pointerは「これまでに何人が登録されたか」を示すカウンタである(いま考えると名前があまり良くなかった)。原子全体にたいして、
- 番地を調べる (particle_position[i]にキャッシュしてある) → pos番地だったとする
- その番地の住人の最初の場所(indexes[pos])から、これまでにpos番地に登録された人数(pointer[pos])だけずれたところに自分の番号を登録する。
- pos番地に登録された人数を増やしておく(++pointer[pos];)。
という手続きをすれば、最終的にsorterd_bufferに番地番号でソートされた原子インデックスが入る。実際のソースは以下の通り。
for(int i=0;i<pn;i++){
int pos = particle_position[i];
int j = indexes[pos] + pointer[pos];
sorted_buffer[j] = i;
++pointer[pos];
}
住所録から逆引きして探索
住所録ができたら、そこから逆引きして調べる。二つとなりの番地と相互作用が届かないようにブロックサイズを決めたので、一次元であれば、n番地と相互作用する可能性があるのはn-1番地とn+1番地のみである。作用反作用を考慮すれば、n番地とn+1番地だけ調べれば良い。このうち、n番地内を調べる場合と、n番地とn+1番地を調べる場合は別処理になる。
その登録処理をしているのが、MeshList::search(int id, Variables *vars, std::vector &pairs)である。int idは、id番地についての処理で、まず隣接番地の探索ののち、id番地内での相互作用ペア探索を行う。
3次元の場合、ある区画に隣接する区画は26個ある。作用反作用で半分に落とすため、調べるべき区画は13箇所となる。
それが以下の13行に対応する。
search_other(id, ix + 1, iy, iz, vars, pairs);
search_other(id, ix - 1, iy + 1, iz, vars, pairs);
search_other(id, ix , iy + 1, iz, vars, pairs);
search_other(id, ix + 1, iy + 1, iz, vars, pairs);
search_other(id, ix - 1, iy , iz + 1, vars, pairs);
search_other(id, ix , iy , iz + 1, vars, pairs);
search_other(id, ix + 1, iy , iz + 1, vars, pairs);
search_other(id, ix - 1, iy - 1, iz + 1, vars, pairs);
search_other(id, ix , iy - 1, iz + 1, vars, pairs);
search_other(id, ix + 1, iy - 1, iz + 1, vars, pairs);
search_other(id, ix - 1, iy + 1, iz + 1, vars, pairs);
search_other(id, ix , iy + 1, iz + 1, vars, pairs);
search_other(id, ix + 1, iy + 1, iz + 1, vars, pairs);
隣接番地との探索、自身の番地内の探索は、番地内にいる原子数をnとしてO(n^2)の手間がかかる。ただし、このnは、全原子数Nが増えても増えないため、全体の探索の手間はO(N)となる。
以上の処理を全ての番地について行えば良い。それを行っているのがMeshList::make_pairの最後の処理である。
for (int i=0;i<number_of_mesh;i++){
search(i, vars, pairs);
}
結果
さて、これで全ての処理がO(N)となった。まず、これまでのL=10で計算してみる。
$ time ./a.out > energy.dat
./a.out > energy2.dat 5.08s user 0.12s system 99% cpu 5.200 total
Step 2までの計算が 5.730秒とかだったので、たいして高速化されていない。これはもちろんLが小さいからで、大きなシステムサイズではより高速化が顕著となる。
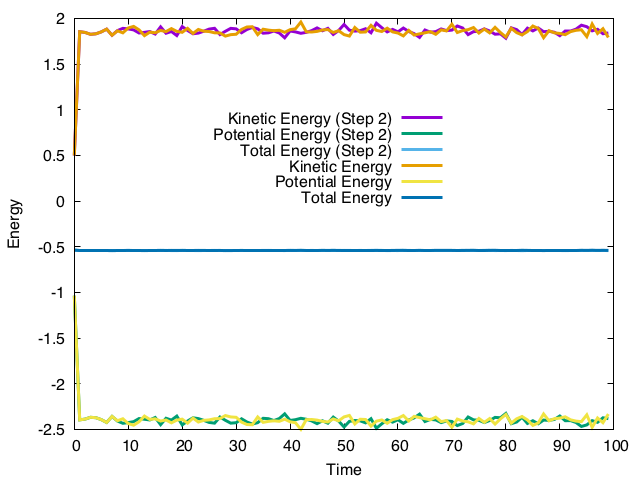
ここで注意しなければならないのは、ペアリストの登録の順番が異なるため、エネルギーなどの結果が変わることである。
Step 2の計算と、最初は一致しているが、徐々にずれていき、t = 10からは完全に別の時間発展をしていることがわかる。これは足し算の順番が変わったことによる誤差が蓄積したもので、MDにつきものの現象である。
システムサイズを倍のL=20 (4000原子)にすると、速度差がはっきりする。
# Step 2
$ time ./a.out
./a.out 237.33s user 1.17s system 99% cpu 3:58.81 total
# Step 3
$ time ./a.out
./a.out 30.91s user 0.87s system 99% cpu 31.805 total
O(N^2)では237秒かかる計算が、32秒で完了する。
まとめ
Step 2でペアリストを導入し、ペアリスト構築以外はO(N)に落とした。Step 3ではメッシュ探索1を実装し、ペアリスト構築の手間をO(N)に落としたため、これで全アルゴリズムがO(N)となった。Bookkeeping法が手軽に導入できるのにたいし、メッシュ探索はわりと面倒だ。Step 2までのコードが384行だったのに、メッシュ探索コード(meshlist.cpp, hpp)だけで156行ある。また、メッシュ探索をすると力の足し上げの順序が変わり、時間発展結果が変わるのもデバッグを面倒にする。しかし、ある程度以上大きな系を計算するにはO(N)のアルゴリズムに落とすのは必須であり、そのためにもメッシュ探索は書かないといけない。
ここまでのコードはgithub/kaityo256/mdstep/step3においてある。
おまけ:デバッグのコツ
メッシュ探索によるペアリスト構築のデバッグには、sort diffデバッグが有効である。初期条件を作った後、もしくはしばらく時間発展した後に、O(N^2)によるペアリスト構築とメッシュ探索による構築をそれぞれやって、ペア情報をダンプする。この際、若い番号を左に表示するようにしておく。同じ条件を与えられれば、同じペアリストを構築するはずであるが、順序が変わるため、ソートする。
例えばO(N^2)で構築したペアリストをダンプする状態で、
$ ./a.out | sort > o2.dat
メッシュ探索で構築したペアリストをダンプする状態で、
$ ./a.out | sort > o1.dat
そして、双方のdiffを取り、違いがなければデバッグ完了である。初期条件だけでなく、しばらく時間発展した後のチェックもしたほうが良い。また、周期的境界条件の扱いも面倒である。ペアリスト構築前に必ず周期的境界条件補正を行い、領域からはみ出した原子はいない状態でペアリスト構築を行うか、ペアリスト構築時にはみ出している原子がいることを想定するかを決める必要がある。今回のコードでは安全側に倒し、ペアリスト構築時にはみ出している原子がいる可能性を考慮して補正を行っている。
-
筆者は便宜的にこう呼んでいるが、一般的な呼び方なのかは知らない。 ↩