分子動力学法ステップ・バイ・ステップ その1

はじめに

古典分子動力学法(Molecular Dynamics Method, MD)は多くの優れた実装があり、もはやゼロから手で書く時代ではないかもしれない。でも、アプリケーションをブラックボックスとして使うのは危険だし、自分が使う手法くらい、一度はフルに自分で書いてみる経験をしておくのも悪くないと思う。

というわけで、MDをゼロから書いてみる。目標は、カットオフのあるLennard-Jones (LJ)ポテンシャルのMDにおいて、アルゴリズムでの高速化を一通り実装すること。具体的には、

• ポテンシャルはLJのみ
• 原子は一種類のみ
• 系は三次元
• シミュレーションボックスは立方体
• 周期的境界条件

といったMDを組む。実装する高速化アルゴリズムは

• メッシュによるO(N)隣接粒子探索
• Bookkeeping法による相互作用粒子リストの使い回し
• 相互作用相手でのソート

程度にとどめ、原則としてチューニングはしない。また、言語としてC++を使う。autoキーワードなど、一部C++11の機能も使うことにする。

コードは逐次github/kaityo256/mdstepで公開する予定。

• その1　 $O(N^2)$のルーチンまで ← イマココ
• その2　 ペアリストの構築とBookkeeping法
• その3　 メッシュ探索
• その4 　少しだけ高速化
• その5 　温度制御法を三種類実装してみる
• その6 　圧力測定ルーチンの実装

Step 1

最初は、大雑把なクラス設計を考える。クラスで管理するほど大きなコードではないが、C++に慣れているプログラマだとクラスわけしたほうが理解がしやすいかもしれないので。今回はO(N^2)のコードを組む。

システムパラメタ (systemparam.*)

系のサイズや、カットオフ距離、時間刻みなどのシステムパラメタはまとめてsystemparam.hppに書いておこう。また、後の便利のために周期的境界条件の補正コードもここに突っ込んでおく。カットオフはとりあえず2.0くらいにしておこう。システムサイズも10にしておく。

変数管理クラス (Variables)

まず、原子の情報として、座標と運動量を保持する必要があるので、そういう構造体を作ろう。

struct Atom {
  double qx, qy, qz;
  double px, py, pz;
};

位置と速度をx,y,z,vx,vy,vzで定義する流儀もあるが、ここはハミルトンの運動方程式を解いていると思うことにして、一般化座標と一般化運動量の気持ちでqx,qy,qz,px,py,pzを使う。これをまとめてstd::vectorで管理する。

std::vector<Atom> atoms;

これは、構造体の配列(Array of Structures, AoS)という方式で、実は逆の配列の構造体(Structure of Arrays, SoA)の方が高速な場合が多いのだが、気にしないことにする。また、伝え聞くところによると、std::vectorを使うと遅いので生配列を使わざるを得ないタコなコンパイラというものがあるそうなのだが、僕はよく知らないので遠慮なくvectorを使う。

その他、系の時刻(time)などをまとめて、Variablesというクラスで管理することにする。

後の便利のために、Variablesにいくつかメソッドを追加しておく。まず必要なのが、原子を追加するインタフェース。これは座標を受け取って単にpush_backするだけ。

void
Variables::add_atoms(double x, double y, double z) {
  Atom a;
  a.qx = x;
  a.qy = y;
  a.qz = z;
  a.px = 0.0;
  a.py = 0.0;
  a.pz = 0.0;
  atoms.push_back(a);
}

運動量はゼロクリアしておこう。

次に、初速を与えるメソッドもあった方が良い。これはset_initial_velocityという名前で作っておく。引数の大きさで、向きを3次元方向にランダムに向ける。ついでに、全体の平均運動量をさっぴいておく。そうしないと原子全体がドリフトしてしまって、温度などが正しい結果を与えない。

もう一つ、あると便利なのが、コンフィグレーションのダンプ、具体的にはcdviewという描画ソフト用のファイルを吐くメソッド。cdviewというのは古石さんが作成した粒子座標の可視化ツールで、多機能であるが、とりあえず「粒子番号、粒子種、座標」をずらずら並べたファイルを連番で吐いて、

$ cdview *.cdv

などとして読み込ませるとアニメーションで表示してくれるため、MDの動作確認に便利。これはexport_cdviewという名前で実装しておこう。呼ぶ度に連番でファイル(confXXX.cdv)というファイルを吐くようにしておく。

原子数を返す関数も用意しておこう。単にstd::vector::sizeのラッパーでよい。

観測クラス (Observer)

次に、エネルギー等の観測を行うクラスを作る。特にクラスに分ける必要は無く、かつインスタンスを作る必要も無いのだが、作者の趣味で分ける。Variablesクラスのインスタンスを受け取って温度やエネルギーを返すメソッドを持つ。例えば運動エネルギーなら、

double
Observer::kinetic_energy(Variables *vars) {  double k = 0;
  for (auto &a : vars->atoms) {
    k += a.px * a.px;
    k += a.py * a.py;
    k += a.pz * a.pz;
  }
  k /= static_cast<double>(vars->number_of_atoms());
  return k * 0.5;
]

のように書ける。無意味にautoを使っているので、コンパイルには-std=c++11が必要となる。2016年にもなってC++11に対応していないコンパイラは無視する。なお、エネルギーは原子数で割って原子あたりの量にしておくと、サイズを変えた時にもあまり値が変わらないのでいろいろ便利である。

ポテンシャルエネルギーは、とりあえずO(N^2)で組む。チューニングは考えないと書いたが、いちいちvars->atoms[i].pxなどと、なんども参照の解決をしなければならない形に書くのは気が引けるので、生配列の形にキャストしてしまう。

  Atom *atoms = vars->atoms.data();

これで、あたかもAtom atoms[N];といった生配列のように扱うことができる。

なお、カットオフを入れている場合、力の計算は変更は無いが、ポテンシャルエネルギーの計算ではカットオフでちょうどゼロとなるように定数を足す必要があることに注意。

MDクラス (MD)

MDクラスを作るかどうかは正直微妙なところだが、VariablesクラスとObserverクラスのインスタンスを管理するクラスとして実装することにしよう。コンストラクタでこれらのクラスのインスタンスを作り、デストラクタで消す。また、初期条件もこいつに作らせよう。

初期条件は、面心立方格子(FCC)で組むことにする。立方格子で組むと、特に高密度の時に原子間距離が近すぎ、緩和に時間がかかる。また、下手な初期配置を組むと、周期的境界条件で左端と右端の原子が近すぎで吹っ飛ぶ、なんてこともあるので注意が必要である(経験者)。FCCは、単位格子に4つ原子がいるので、格子定数を2とすると、密度が0.5になっていろいろちょうど良い。これはmakeconfという関数で用意しておこう。

時間発展は、手軽に二次のシンプレクティック積分を使おう。具体的には

• q ← q + pdt0.5
• p ← p + f*dt
• q ← q + pdt0.5

とする数値積分である。なので、座標を更新する関数をupdate_position、運動量を更新する関数をcalculate_forceという名前にすると、1ステップは

  update_position();
  calculate_force();
  update_position();
  periodic();
  vars->time += dt;

みたいに書ける。periodicというのは、領域からはみ出した原子の位置を調整する関数。
力の計算も、O(N^2)でよければ簡単に書ける。

void
MD::calculate_force(void) {
  const int pn = vars->number_of_atoms();
  Atom *atoms = vars->atoms.data();
  for (int i = 0; i < pn - 1; i++) {
    for (int j = i + 1; j < pn; j++) {
      double dx = atoms[j].qx - atoms[i].qx;
      double dy = atoms[j].qy - atoms[i].qy;
      double dz = atoms[j].qz - atoms[i].qz;
      adjust_periodic(dx, dy, dz);
      double r2 = (dx * dx + dy * dy + dz * dz);
      if (r2 > CL2)continue;
      double r6 = r2 * r2 * r2;
      double df = (24.0 * r6 - 48.0) / (r6 * r6 * r2) * dt;
      atoms[i].px += df * dx;
      atoms[i].py += df * dy;
      atoms[i].pz += df * dz;
      atoms[j].px -= df * dx;
      atoms[j].py -= df * dy;
      atoms[j].pz -= df * dz;
    }
  }
}

adjust_periodicというのは、周期的境界条件の補正をする関数。CL2はsystemparam.hppで定義した、カットオフ距離の平方で、カットオフ距離よりも距離が離れていればそのペアについては力の計算をしない。

あとは、MDを実行するメソッドrunを作って、main関数からはただそれを呼ぶだけにする。

int
main(void) {
  MD *md = new MD();
  md->run();
  delete md;
}

検証

以上でMDは完成である。実行して、エネルギーが保存していることを確認しよう。MD::runとしてこんな関数を書く。

void
MD::run(void) {
  makeconf();
  const int STEPS = 10000;
  const int OBSERVE = 100;
  for (int i = 0; i < STEPS; i++) {
    if ( (i % OBSERVE) == 0) {
      double k = obs->kinetic_energy(vars);
      double v = obs->potential_energy(vars);
      std::cout << vars->time << " ";
      std::cout << k << " ";
      std::cout << v << " ";
      std::cout << k + v << std::endl;
      vars->export_cdview();
    }
    calculate();
  }
}

1万ステップ計算し、100ステップごとに運動エネルギー、ポテンシャルエネルギー、全エネルギーを表示し、cdview用の位置をダンプするコードになっている。

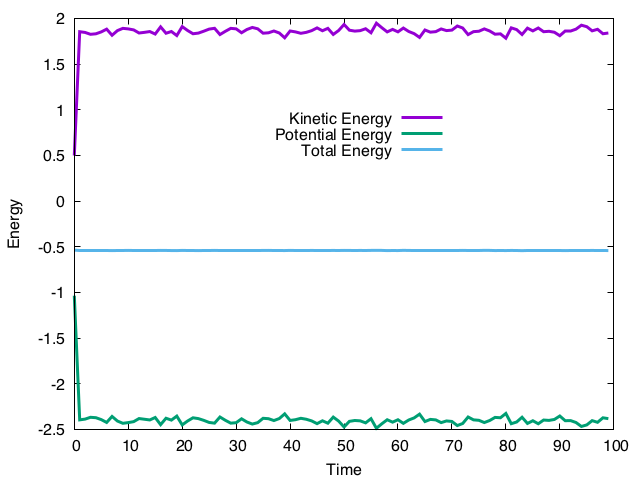
実行結果はこんな感じ。

運動エネルギーとポテンシャルエネルギーは揺らいでいるが、全エネルギーはそれなりに保存しているので、正しく計算できているようだ。

cdviewから連番ビットマップを吐いてconvertでアニメーションgifにすることもできる。

まとめ

O(N^2)のMDコードを組んでみた。クラスに分けたりしたので無駄にコードが増えたが、それでも300行程度でMDを実行し、可視化用のデータも吐けるコードが組める。手元のPCでは、500原子の1万ステップの計算は20秒程度でできる。数千原子程度までならO(N^2)で十分実用的に動く。ただし、1万原子を超えるとO(N^2)ではつらくなるので、O(N)に落とさなければならない。というわけでこれからアルゴリズムレベルの最適化を進めて行くことにする。