みなさん、山に登っていますか?>直喩
僕はまだあまり登れていません。
ARM SVEの組み込み関数の使い方の解説を続けます。
コードを以下に置いておきます。まだ開発中なので、記事を書きながら修正していくと思います。
https://github.com/kaityo256/sve_intrinsic_samples
コンパイル、実行方法については「その1」を見てください。
水平演算について
SIMDによるベクトル演算は、複数のデータを保持するSIMDレジスタの、「要素ごと」の演算を実行します。例えば512ビットのレジスタなら倍精度実数(double)を8個保持できるため、それぞれのレジスタがdouble a[8], b[8]となっており、c=a+bは、
double c[8];
for(int i=0;i<8;i++){
c[i] = a[i]+b[i];
}
という演算を意味します。
さて、数値計算では、リダクション(reduction)と呼ばれる処理が頻出します。典型例が総和です。こんなイメージです。
double sum(double *a, const int n){
double s = 0.0;
for(int i=0;i<n;i++){
s += a[i];
}
return s;
}
このような計算を行うために、SIMDレジスタ内で総和をとったりする演算が用意されており、水平演算 (horizontal operations)と呼ばれます。本稿では、ARM SVEの水平演算をいくつか見てみます。
水平加算
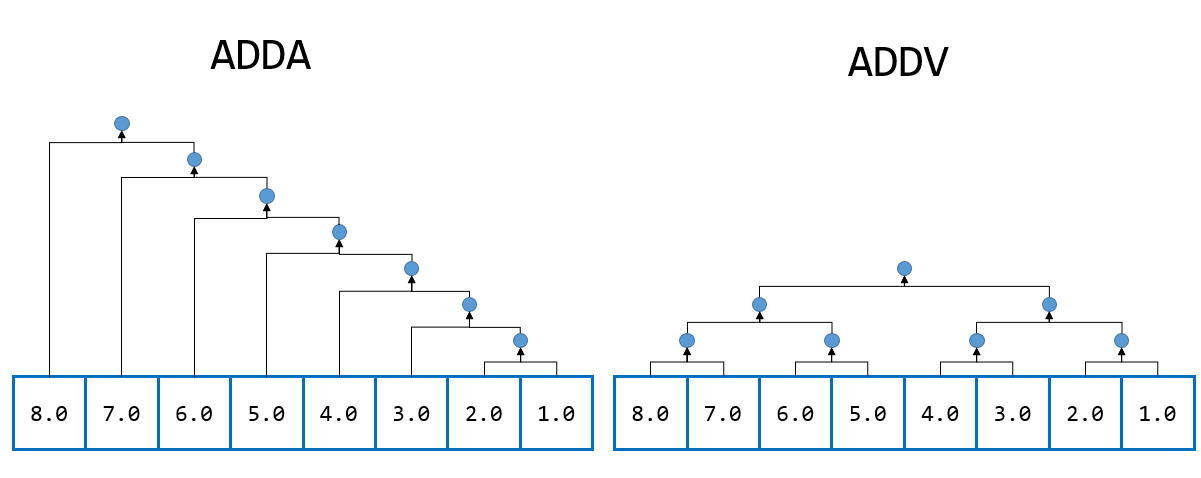
水平加算とは、SIMDレジスタ内の要素の総和を返す演算です。ARM SVEには、水平加算用の命令としてADDAとADDVが用意されています。ADDAは、素直に左から足していくのにたいして、ADDVはペアごとに足していきます。こんな感じです。
なのでADDAに比べてADDVの方が倍近く早いですが、ADDAはスカラーループと同じ結果が得られるのに対して、ADDVは場合によっては異なる結果を与えることがあります。
桁落ちの様子がわかりやすいように、$10^{-8}$と$10^8$が交互にならんだ8個のデータをSIMDレジスタにロードして、水平加算してみましょう。
void add_vector() {
const double a = 1e-8;
const double b = 1e8;
double d[8] = {a, b, a, b, a, b, a, b};
svbool_t tp = svptrue_b64();
svfloat64_t va = svld1_f64(tp, d);
float64_t sum = svadda_f64(tp, 0.0, va);
printf("adda = %.15f\n", sum);
float64_t sum2 = svaddv_f64(tp, va);
printf("addv = %.15f\n", sum2);
}
結果はこうなります。
adda = 400000000.000000000000000
addv = 400000000.000000059604645
両者の結果がずれていることがわかると思います。
ADDAが素直なループ、ADDVがツリー型の和であることを確認するため、等価なスカラーコードを書いてみましょう。
void add_scalar() {
const double a = 1e-8;
const double b = 1e8;
double d[8] = {a, b, a, b, a, b, a, b};
double sum = 0.0;
for (int i = 0; i < 8; i++) {
sum += d[i];
}
printf("adda = %.15f\n", sum);
double s1 = d[0] + d[1];
double s2 = d[2] + d[3];
double s3 = d[4] + d[5];
double s4 = d[6] + d[7];
double s12 = s1 + s2;
double s34 = s3 + s4;
double sum2 = s12 + s34;
printf("addv = %.15f\n", sum2);
}
実行結果はこうなります。
adda = 400000000.000000000000000
addv = 400000000.000000059604645
それぞれ、先ほどのADDA、ADDVを使った場合と同じ結果が得られたのがわかるかと思います。
最大値
リダクション演算で頻出するパターンとして、最大値、最小値を求めるものがあります。ARM SVEでは、最大値を求める命令としてMAXVとMAXNMVの二つがあります。この二つはNaNの扱いが異なります。MAXVは、要素のうち一つでもNaNがあればNaNを返します。しかし、MAXNMVは要素が全てNaNの時にはNaNを返しますが、それ以外の場合はNaNを無視します。
まずはNaNがない場合を試してみましょう。その場合はMAXVとMAXNMVの動作は同じなのでMAXVだけ見てみます。
void maxv() {
const int n = svcntd();
std::vector<double> a(n);
for (int i = 0; i < n; i++) {
a[i] = (i + 1);
}
std::shuffle(a.begin(), a.end(), std::mt19937());
svbool_t tp = svptrue_b64();
svfloat64_t va = svld1_f64(tp, a.data());
std::cout << "va = " << std::endl;
svshow(va);
float64_t max = svmaxv(tp, va);
std::cout << "max(va) = " << max << std::endl;
}
8個の要素をベクトルレジスタにロードして、svmaxvを呼ぶだけなので簡単だと思います。実行結果はこうなります。
va =
+2.0000000 +8.0000000 +7.0000000 +5.0000000 +6.0000000 +1.0000000 +4.0000000 +3.0000000
max(va) = 8
ベクトルレジスタに(2,8,7,5,6,1,4,3)という値が入っており、最大値として8が返ってきたことがわかると思います。
次に、データの一つにNaNを突っ込んで両者の動作を比べてみましょう。
void maxnmv() {
const int n = svcntd();
std::vector<double> a(n);
for (int i = 0; i < n; i++) {
a[i] = (i + 1);
}
std::shuffle(a.begin(), a.end(), std::mt19937());
a[0] = std::numeric_limits<double>::quiet_NaN();
svbool_t tp = svptrue_b64();
svfloat64_t va = svld1_f64(tp, a.data());
std::cout << "va = " << std::endl;
svshow(va);
float64_t max = svmaxv(tp, va);
std::cout << "maxv(va) = " << max << std::endl;
float64_t maxnmv = svmaxnmv(tp, va);
std::cout << "maxnmv(va) = " << maxnmv << std::endl;
}
配列aの最初の要素a[0]にNaNを突っ込んで、レジスタにロードしてからMAXVとMAXNMVに食わせてみました。実行結果はこうなります。
va =
+2.0000000 +8.0000000 +7.0000000 +5.0000000 +6.0000000 +1.0000000 +4.0000000 +nan
maxv(va) = nan
maxnmv(va) = 8
ベクトルレジスタに(NaN,8,7,5,6,1,4,3)という値が入っており、MAXVはNaNを、MAXNMVは8を返したことがわかるかと思います。MINV, MINNMVも同様です。
まとめ
ARM SVEの水平加算を見てみました。僕はx86系ではあまり水平演算を使ったことがありませんが、さすがに倍精度8要素、単精度16要素と要素数が増えてくると、水平加算の重要度が増してくる気がするので、これから使うかもしれません。
参考文献
ほぼ公式マニュアルしかないのつらい。