はじめに
二次元古典Potts模型をSwendsen-Wangアルゴリズムで更新するモンテカルロ法コードのサンプルを書きました。
コードは以下に置いておきます。
https://github.com/kaityo256/mc/tree/master/potts_2d
Potts模型とは
Q状態強磁性Potts模型とは、スピンが$Q$種類の状態を取ることができ、隣り合うスピンが同じ状態の時にエネルギーが下がるような模型です。ハミルトニアンを書くとこんな感じになります。
$$
H = -J \sum_{i<j} \delta_{\sigma_i, \sigma_j}
$$
Potts模型はIsing模型を素直に拡張した模型になっています。Q個の等価な基底状態があり、低温でそのどれかが選ばれる、といった時にQ状態Potts模型と同じ普遍性を持ったりします。
そういう意味でわりと見かける模型で、かつモンテカルロ法も簡単なのですが、実装しようとすると詰まる部分が結構あったりします。本稿では、僕が論文を読んでわかりづらかったところに留意しつつ、正方格子上における古典Potts模型をSwendsen-Wangアルゴリズムで更新するモンテカルロ法コードを説明してみます。
プログラム
Swendsen-Wangアルゴリズム
スピン系の更新にはMetropolis法などが使われますが、Potts模型はSwendsen-Wangアルゴリズムという、非常に効率の良い方法が使えます。これはスピンをクラスターに分けてクラスターごとにまとめてひっくり返す手法で、クラスターアルゴリズムとか、クラスターアップデート等と呼ばれます。
Swendsen-Wangアルゴリズムは、逆温度を$\beta$として、
- 隣接するスピンが同じ状態の時、$p = 1 - \exp(-\beta)$でつなぐ
- お互いにつながっているスピンをクラスターに分ける
- クラスターごとに新しいスピン状態をランダムに与える
という手続きを繰り返すものです。詳細はSwendsen-Wangアルゴリズムのサンプルコードも参照してください。
このうち、クラスターに分けるところと、スピンをクラスターごとにひっくり返すところが以外に詰まりポイントです。
変数のセットアップ
ではプログラムを書いていきましょう。まずは必要なものをインクルードします。
# include <algorithm>
# include <array>
# include <iostream>
# include <random>
# include <vector>
次に、システムサイズ、スピン数、状態数も定義しておきましょう。手抜きでグローバル変数にします。
int L; // System Size
int N; // Number of Spins
int Q; // Number of States
次は変数の定義です。
std::vector<int> spins, newspins;
std::vector<std::array<int, 2>> neighbor;
std::vector<int> parent;
スピンはとりあえずstd::vectorで定義しましょう。スピン状態はspins、後でひっくり返す時に使うのでnewspinsも定義しておきます。
あと、隣接スピン番号をneighborで定義しておきましょう。二次元配列ですが、右と下しか必要ないのでneighbor[N][2]という形にしておきます。
あと、クラスター番号を管理するUnion-Find木のためにparentという配列も定義しておきます。
初期化
次に初期化をしましょう。
int pos2index(int ix, int iy) {
ix = (ix + L) % L;
iy = (iy + L) % L;
return ix + iy * L;
}
void init(int size) {
L = size;
N = L * L;
spins.resize(N);
newspins.resize(N);
neighbor.resize(N);
parent.resize(N);
// Initialize Neighbors
for (int iy = 0; iy < L; iy++) {
for (int ix = 0; ix < L; ix++) {
int i = pos2index(ix, iy);
neighbor[i][0] = pos2index(ix + 1, iy);
neighbor[i][1] = pos2index(ix, iy + 1);
}
}
}
サイズの与えて、std::vectorのresizeをします。ついでに、スピンの「右」と「下」のスピンのインデックスも計算しておきます。周期境界条件もここで取り込んでおきましょう。そのために、場所からスピンインデックスを返す関数pos2indexを書いておきました。
Union-Find
クラスタリングするためにUnion-Findアルゴリズムを使います。そのためにUnionとFindを書いておきましょう。ちなみに、C++ではunionが予約語なので、同僚さんが代わりにuniteを使っていてなるほど、と思いました。
int find(int i) {
while (i != parent[i]) {
i = parent[i];
}
return i;
}
void unite(int i, int j) {
i = find(i);
j = find(j);
parent[j] = i;
}
Union-FindアルゴリズムについてはUnion-Find木のサンプルコードも参考にしてください。
スピンの接続
UnionとFindがあれば、スピンの接続はそれを呼ぶだけなので簡単です。
void connect(int i, int j, double p, std::mt19937 &mt) {
std::uniform_real_distribution<> ud(0.0, 1.0);
if (spins[i] != spins[j]) return;
if (ud(mt) > p) return;
unite(i, j);
}
関数connecは、スピンiとスピンjが同じ状態なら確率pでつなぐものです。
モンテカルロステップ
関数connectを使うと、スピン状態の更新(MCステップ)の実装は簡単です。
- まずスピンをつなぎ、
- 次にスピンをひっくり返す
という手続きを取ります。そのまま実装するとこんな感じになるでしょう。
void one_step(double beta, std::mt19937 &mt) {
std::uniform_int_distribution<> ud(0, Q - 1);
// Initialize Union-Find tree
for (int i = 0; i < N; i++) {
parent[i] = i;
}
// Connect
const double p = 1.0 - exp(-beta);
for (int i = 0; i < N; i++) {
connect(i, neighbor[i][0], p, mt);
connect(i, neighbor[i][1], p, mt);
}
// Flip
for (int i = 0; i < N; i++) {
newspins[i] = ud(mt);
}
for (int i = 0; i < N; i++) {
spins[i] = newspins[find(i)];
}
}
最初に、Union-Find木の初期化をしています。
次に、全てのスピンについて、「右」と「下」のスピンとの接続チェックをします。
こうして、スピンがクラスターに分かれた後、クラスター毎に新しいスピン状態を与える必要があります。
いろいろ方法はあると思いますが、簡単なのはN個ランダムに0からQ-1の状態を用意しておき(newspins)、各スピンのクラスター番号に対応するスピン状態(newspins[find(i)])にすれば、同じクラスターに属すスピンは同じ状態になり、かつ異なるクラスターに属すスピンはランダムになります。
秩序変数
Q状態Potts模型の秩序変数定義はいくつかありますが、単純なのはQ-1次元のベクトルと思って、平均ベクトルの長さを取るものです。
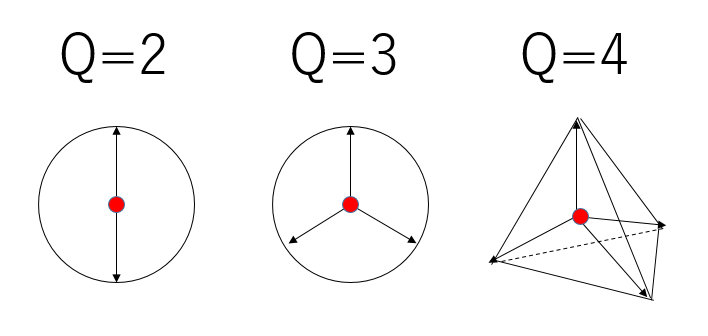
この図の矢印を$\vec{v}_0, \vec{v}_2,\cdots$としましょう。これらはQ=3の時には、正三角形の中心から頂点へ、Q=4の時には正四面体の中心から頂点に向けたベクトルで、長さは1です。
平均ベクトル$\vec{m}$は、
$$
\vec{m} = \sum_{q=0}^{Q-1} m_q \vec{v}_q
$$
で定義されます。$m_q$は、状態$q$を取るスピンの割合です。
$$
m_q = \frac{1}{N} \sum_i \delta_{\sigma_i, q}
$$
ここから$m^2$を計算すると、
m^2 = \sum_{q=0}^{Q-1} m_q^2
+ 2 \sum_{i<j} m_i m_j \vec{v}_i \cdot \vec{v}_j
ここで、異なる向きのベクトルの内積は
$$
\vec{v}_i \cdot \vec{v}_j = \frac{-1}{Q-1}
$$
なので、最終的に、
$$
m^2 = \sum_{q=0}^{Q-1} m_q^2
- \frac{2}{Q-1}\sum_{i<j} n_i n_j
$$
となります。
以上をそのまま実装すると、
double magnetization(void) {
std::vector<double> m(Q, 0.0);
for (int i = 0; i < N; i++) {
m[spins[i]] += 1;
}
for (int i = 0; i < Q; i++) {
m[i] /= static_cast<double>(N);
}
double m2 = 0.0;
for (int i = 0; i < Q; i++) {
m2 += m[i] * m[i];
}
for (int i = 0; i < Q - 1; i++) {
for (int j = i + 1; j < Q; j++) {
m2 -= 2.0 * m[i] * m[j] / (Q - 1);
}
}
return m2;
}
です。これで秩序変数の二次のモーメント$m^2$が計算できます。
ビンダー比
相転移を調べるには、ビンダー比と呼ばれる量を計算すると便利です。ビンダー比は、以下のように定義されます。
U = \frac{\left<m^4\right>}{\left<m^2\right>^2}
ビンダー比は、臨界点直上においてシステムサイズ依存性を持ちません。そこで、この量の温度依存性を調べ、異なるシステムサイズについてプロットすると一点で交わり、それが臨界点になります。
指定の逆温度において、最初に適当に緩和させ、$m^2$ と $m^4$ を測定し、最後にビンダー比を出力するコードはこんな感じになります。
void mc(double beta) {
std::mt19937 mt;
for (int i = 0; i < thermalize_loop; i++) {
one_step(beta, mt);
}
double sm2 = 0.0;
double sm4 = 0.0;
for (int i = 0; i < observe_loop; i++) {
one_step(beta, mt);
double m2 = magnetization();
sm2 += m2;
sm4 += m2 * m2;
}
sm2 /= static_cast<double>(observe_loop);
sm4 /= static_cast<double>(observe_loop);
double u = sm4 / sm2 / sm2;
std::cout << beta << " " << sm2 << " " << u << std::endl;
}
結果
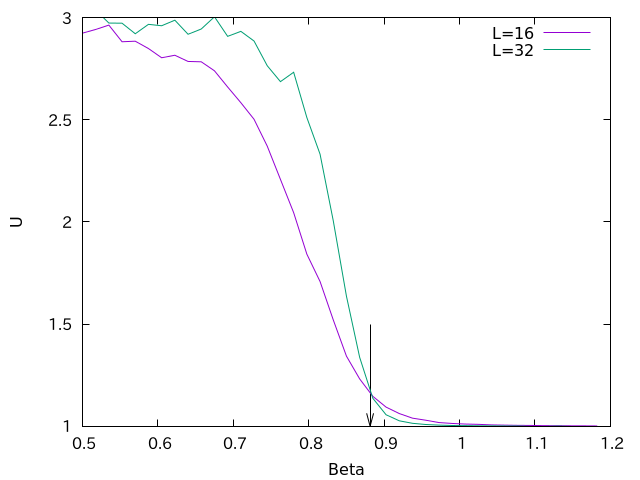
正方格子上におけるQ状態Potts模型の臨界点$\beta_c$は
$$
\beta_c = \log(1+\sqrt{Q})
$$
で定義されます。Q=2、すなわちIsing模型の場合のビンダー比の温度依存性はこんな感じになります。
確かに臨界点上で異なるシステムサイズのビンダー比が交差しています。
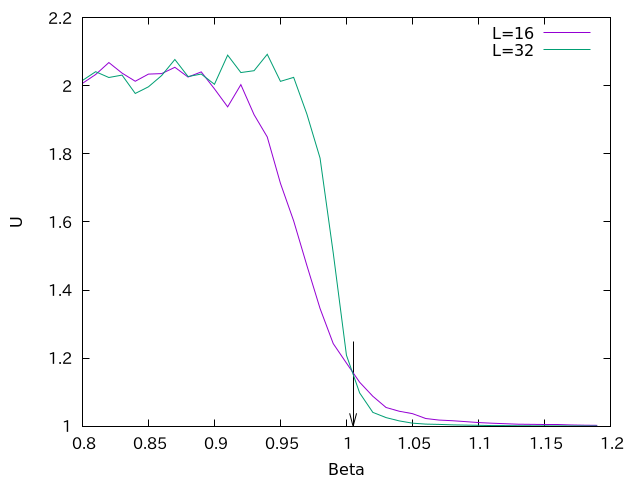
Q=3の時も同様です。
まとめ
正方格子上のPotts模型のモンテカルロシミュレーションコードについて説明してみました。100行ちょっとのコードなので、慣れるとすぐに書けるのですが、論文だけ読んで実装すると戸惑う点が結構あります。個人的には、秩序変数の定義と、スピンをクラスターごとまとめてフリップするところで詰まりました。
本稿が誰かの助けになれば幸いです。