はじめに
スピン系をモンテカルロシミュレーションする時、Swendsen-Wangアルゴリズムという非常に有効な方法があるのですが、これを、例えばIsing modelに適用しようと思って「swendsen wang ising sample code」でググったら自分がすごい昔に適当に書いたコードが最上位に表示されまして。これってあんまり良くないな、と思って解説記事を書こうと思った次第です。
本稿ではSwendsen-Wangアルゴリズムを実装する前に、サイトパーコレーションを例としてUnion-Find木を使ったクラスタリングの説明をします。ソースコードは以下においておきます。
クラスタリング
クラスタリング(clustering)とは、データを適当な基準で分類することです。通常は統計学で「似ているデータ同士をなるべくうまく分類する」といった文脈で使われることが多いのですが、スピン系のモンテカルロをやる人は、「同値関係が与えられた時に、データを同値類に分類すること」という意味で使うことが多いので注意が必要です。
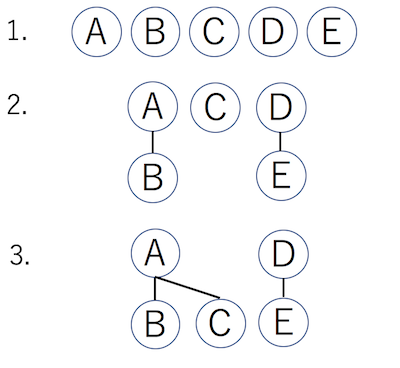
たとえば、A, B, C, D, Eの5人がいて、そこに「AさんとBさんは友達」「DさんとEさんは友達」「BさんとCさんは友達」という情報が与えられたとします。ここで「友達の友達は友達である」という条件を与えると、「A, B, C」「D, E」という二つの友達グループにわけることができます。
このように「A, B, C, D, E」という要素の集合と、「A=B, D=E, B=C」といった同値関係の集合を与えられた時に「任意の要素が同じ同値類に属しているか」という情報が欲しくなります。これを実装するのがUnion-Find木です。
Union-Find
概念
「同値類の分類」を行うのに、便利な操作が二つあります。FindとUnionです。
- Find: ある要素がどの集合に属しているか調べる
- Union: 二つの集合を一つにまとめる
この操作を実装するのに使われるのがUnion-Find木です。
先程の友達の例で説明してみます。
- まずA, B, C, D, Eがそれぞれ単体でノードになっています。
- 「A=B」「D=E」を処理します。この時、どうつないでもいいのですが、とりあえず文字コードが若い方を親にします。
- 「B=C」を処理します。これも、どうつないでもよいのですが、とりあえずCをAの子ノードにします。
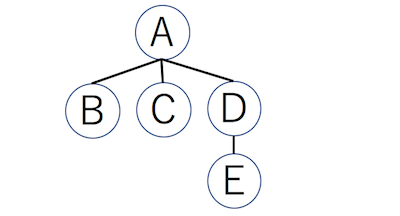
これでクラスタリング終了です。クラスタリング後は、各ノードがなんらかの木に属しています(ノードとして自分自身しか含まない木もありえます)。その木の根ノードを、グループの代表とすることにします。この時、「Aさんグループ」と「Dさんグループ」に別れたことになります。
この構造ができた時、まずFind操作、すなわち任意の要素がどのグループに属すかを調べるには、そこから親を辿っていって、根まで到達した時の代表ノードを調べれば良いことになります。
また、Union操作、すなわちグループ同士を同じグループにまとめる場合、いろんなやり方がありますが、もっとも簡単には、片方の代表ノードをもう片方の代表ノードにまとめてしまいます。
例えば先の例で「A, B, C」「D, E」のグループに別れた後に、さらに「B=E」という情報が与えられた時、Eさんの所属するグループの代表ノードであるDさんを、Bさんの所属するグループの代表ノードであるAさんの下につけます。
これも様々なくっつけ方がありますが、最も単純な方法を採用しました。
実装
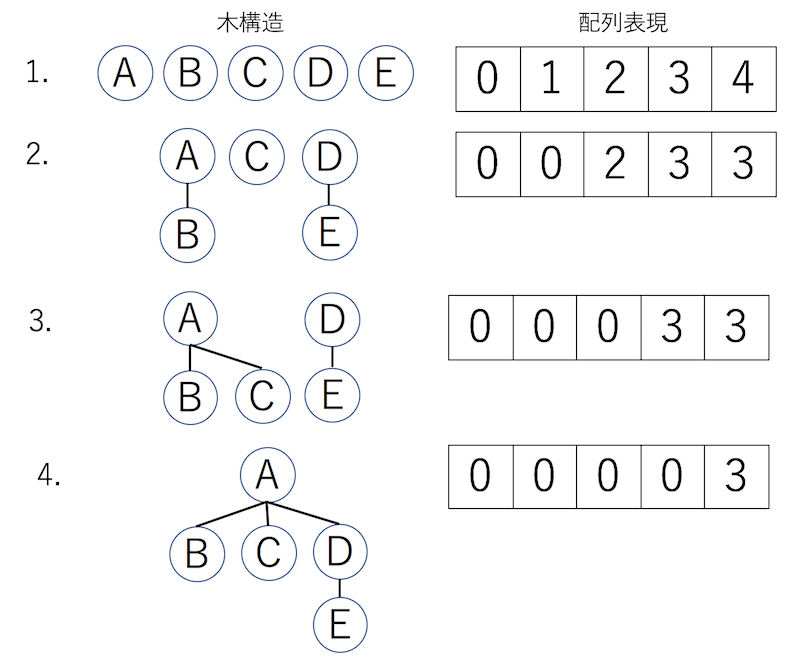
Union-Find木の実装は様々な方法がありますが、実装が簡単な一次元配列を使った方法を紹介します。まず、各ノードに対応したサイズの配列を用意します。
- まず配列の中身はインデックスと一致させておきます。
- 二つをつなぐ場合、それぞれのクラスタ番号(根の番号)のうち、番号が若い方の数字を、そうでない方のインデックスに入れます。この例では、配列の1番に0を代入することでA(クラスタ番号0)とB(クラスタ番号1)をつなぐ処理が実行されたことになります。図は「A=B」「D=E」が処理された後の状態です。
- 「B=C」を処理する際も、Bのクラスタ番号(現在は0番)とCのクラスタ番号(現在は3番)を比較し、インデックス3に0を代入します。
以上でクラスタリング終了です。全てが同じクラスタに属しているのに、配列が全て同じ値になっていないことに注意してください。この配列はそれぞれのインデックスの直接の親を表現しています。
この配列から、任意のノードのクラスタ番号を知ることができます。例えばEさん(番号4)のクラスタ番号を知りたい場合、
- 配列[4]を見ると3と記載されているので、親が3番だということがわかる。
- 配列[3]を見ると0と記載されているので、親が0番だということがわかる。
- 配列[0]を見ると0となり、インデックスと値が一致したので根に到達したことがわかる。
ということでクラスタ番号を得ることができます。配列をtとし、インデックスiのクラスタ番号を知りたい場合、
def get_root(i,t)
while i != t[i]
i = t[i]
end
i
end
とかけます。非常に簡単です。
パーコレーションへの応用
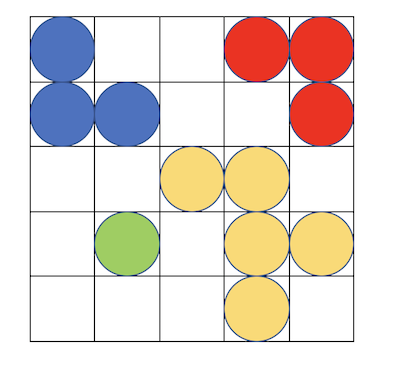
このUnion-Findを利用した例として、サイトパーコレーションを考えてみます。碁盤の目のような格子を考えます。このマスにランダムに石を置いていきます。ここで、「上下左右に隣り合う石は同じグループに属す」と定義します。こんな感じです。
同じグループに属す石を同じ色で塗り分けています。石一つだけが所属する「ぼっちグループ」も存在しています。
さて、この系は石の数が少ない時には多くのクラスタに分かれていますが、石の数を増やしていくと、突然大部分の石がごそっとつながる瞬間が訪れます。これをパーコレーション(浸透)転移といいます。Union-Findを使ってこのパーコレーションをシミュレートしてみましょう。
一辺Lの正方格子を考えます。マスの数はN=L*Lです。このマスに確率0.5で石を置きます。石があるかないかを表現する配列をsにすると、こんな感じになります。
s = Array.new(N){(rand < 0.5)}
また、これらのクラスタ番号を管理する、Union-Find木を表現する配列をtとします。初期化も一緒にやっておきましょう。
t = Array.new(N){|i| i}
さて、クラスタリングは、ある石があるマスを見て、上や右に石があれば、その石の所属するグループをまとめる(Union)することです。クラスタリングはこんな感じに書けるでしょう1。
def clustering(t,s)
L.times do |y|
L.times do |x|
connect(x,y,x+1,y , t, s)
connect(x,y,x ,y+1, t, s)
end
end
end
connect(x1, y1, x2, y2, t, s)は、座標(x1, y1)と座標(x2, y2)の両方に石があったらUnion処理をする関数です。実装するのは難しくないでしょう。
def connect(x1, y1, x2, y2, t, s)
return if x2 == L
return if y2 == L
i1 = x1 + L * y1
i2 = x2 + L * y2
return if !s[i1]
return if !s[i2]
c1 = get_root(i1, t)
c2 = get_root(i2, t)
if c1 < c2
t[c2] = c1
else
t[c1] = c2
end
end
単純に、x2やy2がはみ出していないか、かつ両方に石がある場合に、それぞれの石の所属するグループ番号をget_rootで取得し、その番号の若い方をそうでない方に書き込んでいるだけです。
これを実行した後は、get_root(i,t)を実行すれば、番号iの石の所属するグループ番号が取得できます。それを利用して、石の状態とグループ番号を表示するコードを書いてみましょう。
def show(t,s)
N.times do |i|
puts if (i != 0 && i % L) == 0
if s[i]
printf "%02d ",get_root(i,t)
else
print " "
end
end
puts
end
実行するとこんな感じになります。
$ ruby uf.rb
01 01 01 05 05 05
01 01 05 05
16 01 05 05
25 05 05 05 05
34 05 05
40 05 05 46
05 53 53
56 56 53 53 53
石のあるところだけグループ番号が表示されています。上下左右につながった石は同じ番号になっていることがわかるかと思います(斜めはつながりません)。実行するたびに結果が変わるので何回か実行して正しくクラスタリングできているか確認してください。
まとめ
一次元配列を使ったUnion-Find木を実装し、それを利用してサイトパーコレーションをシミュレートしてみました。なお、上記のようなナイーブな実装では処理が遅くなることが知られています。その高速化については、例えば参考に挙げたスライドを参照してください。
参考
-
明らかに
connectを呼ぶ前に座標x,yに石があるか調べるべきですが、ここはソースの読みやすさを重視してこういう書き方にしています。 ↩