G-Sアルゴリズム
1.はじめに
今回のゼミナールでは、各個人がマッチする対象に関する希望順位を持つマッチング問題において安定マッチング(変化が起こりにくく、全員がそれなりに満足できるマッチング)を効率的に求めるG-Sアルゴリズム(Gale-Shapleyアルゴリズム)を学んだ。本稿ではその内容について解説したいと思う。
2.G-Sアルゴリズム概要
(a)安定マッチング
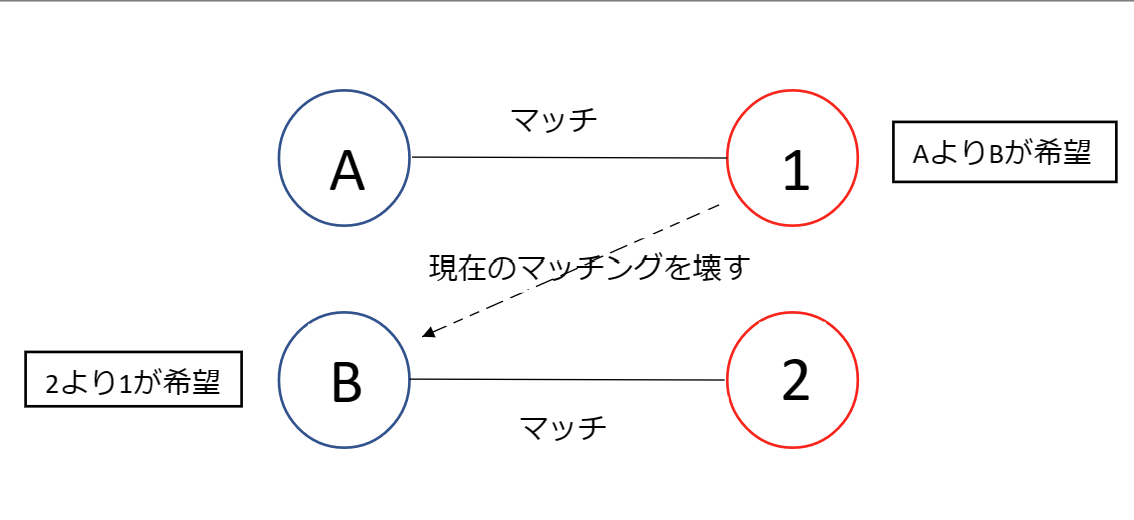
安定マッチングとは不安定性のないマッチングのことである。では、マッチングにおける不安定性とは何だろうか。図1にあるように、1は現在マッチングしているAよりBとマッチングしたいと思い、Bも現在マッチングしている2より1とマッチングしたいと思っている。この時、マッチングしていない者同士の二人組でお互い今の相手よりも希望順位が高いペアが存在し、現在のマッチングを壊す。このようにマッチングを壊しかねない危険なペアをブロッキングペアという。ブロッキングペアが存在することをマッチングにおける不安定性としている。そして、この不安定性がない安定マッチングでは、現在のマッチ相手と離れて違うマッチング可能な人とマッチングしてもメリットがない状況になるので、マッチングに変化が起きにくいのである。
図1(著者が作成)
(b)G-Sアルゴリズムの仕組み
G-Sアルゴリズムは応募側の希望順位リストと受け入れ側の希望順位リストを与えてあげれば安定マッチングを返してくれるアルゴリズムである。よって、必要なのは応募側の希望順位リストと受け入れ側の希望順位リストのみである。これを基に以下の①から④の操作を繰り返すことで安定マッチングを返す。
①応募者は最も希望順位が高い相手に応募する。複数の応募を受けた受け入れ側はその中で希望順位が最も高い応募者を選んで仮マッチングする。他はお断りする。
②断られた応募者は希望順位リストから、その相手を削除して、残りの希望順位リストにいる候補の中で最も希望順位が高い相手に応募する。
③もうすでに仮マッチングしている受け入れ側が、現在仮マッチングしている応募者より希望順位が高い応募者から応募があった場合は、仮マッチングの相手を希望順位が高いほうの応募者に乗り換える。
④どの応募者もすでにマッチングしている、またはもう応募する候補がいない状態になったらアルゴリズムが終了する。その状態になるまでは②③を繰り返す。
応募側と受け入れ側の役割を入れ替えてアルゴリズムを動かしても出力は安定マッチングとなる。しかし、この場合同じマッチングになるとは限らない。いずれにせよ、応募者は自分がマッチングできる相手の中で最適な相手とマッチングすることができる。つまり、G-Sアルゴリズムは応募する側にとって最適な安定マッチングになっているのである。
3.実例
G-Sアルゴリズムは多くのマッチング問題に対して活用されている。例えば、株式会社日経BPの記事「部署と従業員が「選び合う」ベストマッチな配属―マーケットデザインを活用した人材配置」によると、企業内での従業員の配属後に、従業員に配置の目的とプロセスを明確に説明できないため、従業員のパフォーマンスが上がらないケースも多く、さらに早期退職につながりかねないという大きな課題があった。そこで、G-Sアルゴリズムの導入により、人材配置のミスマッチを解消し、全ての従業員が『自分が行けるなかで最高の部署』に配属され、全ての部署が『自部署が採れる最高の従業員』を配属できるようになる。従業員は、その配属によって自分のキャリア形成ができているという意識を強く持てるメリットも発生した。
4.実装
今回は以下のリンクで公開されているG-Sアルゴリズムの実装を行うコードを実行しながら、G-Sアルゴリズムを理解していく。以下にその概要をまとめていく。
参考文献のリンクは以下のものであり、このレポジトリはアルゴリズム実行のスピード検証を目的としている。https://github.com/13tsuyoshi/DA_algorithms/blob/master/DA_Algorithms.ipynb
① ソースコードの構造
このG-SアルゴリズムのPython実装は、主に2つの関数といくつかの補助関数から成り立っている。まずそれぞれの機能に焦点を当てて解説していく。

(a) 関数 gale_shapley
def gale_shapley(applicant_prefers_input, host_prefers_input, **kwargs):
# コードの詳細は省略
return applicant_matchings, host_matchings
この関数はG-Sアルゴリズムを実装し、与えられた応募者とホストの選好表から安定なマッチングを見つける役割を果たしている。主なパラメーターとしては、応募者とホストの選好表、およびオプションのunmatchフラグがある。
(b) 補助関数 random preference table と pseudo random table
def random_preference_table(row, col, **kwargs):
return preference_table
def pseudo_random_preference_table(row, col, n=1000, **kwargs):
return preference_table
これらの関数は、ランダムな選好表を生成するためのものである。random_preference_tableは通常のランダムな選好表を生成し、pseudo_random_preference_tableは複数の選好パターンからランダムに選んで選好表を生成する。
②ソースコードの詳細
(a)必要なライブラリのインポート
from __future__ import division
import math
import functools # for python3
from random import uniform, normalvariate, shuffle
import numpy as np
import time
numpy : 数値計算を高速かつ効率的に行うために使用されている。
math : mathモジュールは、基本的な数学関数や定数を提供する組み込みモジュール。
いくつかの一般的な関数には、sin(正弦)、cos(余弦)、tan(正接)などの三角関数や、sqrt(平方根)、exp(指数関数)、log(自然対数)などがある。
functools : functoolsモジュールは、高階関数(関数を引数として取る関数)やデコレーター(関数を修飾する関数)をサポートする。
random : 似乱数生成に関する機能を提供する。
(b)カスタムエラークラスの定義
class CustomConditionError(Exception):
def __init__(self, message):
self.message = message
このクラスは、独自の条件エラーを発生させるために使用されている。例外が起きた際にエラーメッセージを表示させることができる。
(c)選好表の型チェックと処理:
# コードから抜粋
unmatch = kwargs.get('unmatch', True)
# 選好表の型チェック。listならnumpyへ変換
applicant_preferences = np.asarray(applicant_prefers_input, dtype=int)
host_preferences = np.asarray(host_prefers_input, dtype=int)
# 選好表の行列数をチェック
app_row, app_col = applicant_preferences.shape
host_row, host_col = host_preferences.shape
# unmatchマークが入力されていない時は、選好表の列の最後にunmatch列をつくる
if not unmatch:
dummy_host = np.repeat(app_col+1, app_row)
dummy_applicant = np.repeat(host_col+1, host_row)
applicant_preferences = np.c_[applicant_preferences, dummy_host]
host_preferences = np.c_[host_preferences, dummy_applicant]
app_col += 1
host_col += 1
この部分では、関数に渡された選好表の型を確認し、リストであればNumPy配列に変換している。また、unmatch フラグによって、未マッチング者を示す列を選好表に追加するかどうかを決定している。
(d)選好表の行列数のチェック
# コードから抜粋
if (app_row != host_col-1) or (host_row != app_col-1):
raise CustomConditionError("選好表の行列数が不正です")
applicant_unmatched_mark = app_col-1
host_unmatched_mark = host_col-1
この部分では、未婚考慮済みの選好表の行列数が条件を満たしているかどうかをチェックしている。条件を満たしていない場合には、CustomConditionError を発生させてエラーメッセージを表示するよう定義されている。
またダミー考慮前のapplicantの選好列数(hostの数)を applicant_unmatched_mark、hostの選好列数(applicantの数)を host_unmatched_markとして保存している。
(e)未マッチング者へのダミーの追加
# コードから抜粋
if not unmatch:
dummy_host = np.repeat(app_col+1, app_row)
dummy_applicant = np.repeat(host_col+1, host_row)
applicant_preferences = np.c_[applicant_preferences, dummy_host]
host_preferences = np.c_[host_preferences, dummy_applicant]
app_col += 1
host_col += 1
この部分では、`unmatch`` フラグが False の場合、未マッチング者を示すためのダミーカラムを各選好表に追加している。(未婚を考慮するこのアルゴリズム実行においてダミー追加の追加を行わなければ、マッチングのループが収束しないといった事態が起こるためである)
(f)主要な変数の初期化とソート
# コードから抜粋
applicant_unmatched_mark = app_col-1
host_unmatched_mark = host_col-1
# ソート
host_preferences = np.argsort(host_preferences, axis=-1)
# コードから抜粋
next_start = np.zeros(app_row, dtype=int)
while len(stack) > 0:
# スタックから1人応募者を取り出す
applicant = stack.pop()
# 取り出した応募者の選好表
applicant_preference = applicant_preferences[applicant]
# 選好表の上から順番にプロポーズ
for index, host in enumerate(applicant_preference[next_start[applicant]:]):
# unmatched_markまでapplicantがマッチングできなければ、アンマッチ
if host == applicant_unmatched_mark:
break
# プロポーズする相手の選好表
host_preference = host_preferences[host]
# 相手の選好表で、応募者と現在のマッチング相手のどちらが順位が高いのか比較する
rank_applicant = host_preference[applicant]
matched = host_matchings[host]
rank_matched = host_preference[matched]
# もし受け入れ側が新しい応募者の方を好むなら
if rank_matched > rank_applicant:
applicant_matchings[applicant] = host
host_matchings[host] = applicant
# 既にマッチしていた相手がダミーでなければ、マッチングを解除する
if matched != host_unmatched_mark:
applicant_matchings[matched] = applicant_unmatched_mark
stack.append(matched)
next_start[applicant] = index
break
この部分がG - Sアルゴリズムのメインループである。簡潔にまとめると未マッチング者が存在する限り、各応募者が選好表に基づいて提案を行い、安定なマッチングを構築する仕組みとなっている。まず未マッチング者を格納しているstackが空でない限り対象者を取り出しapplicantおよびhost双方の選好に基づきループを実行する。つまりこの実行により得られるマッチングはapplicantそれぞれの実行結果の集合であるといえる。
(g)random_preference_table 関数
def random_preference_table(row, col, **kwargs):
unmatch = kwargs.get('unmatch', True)
numpy = kwargs.get('numpy', False)
if numpy:
li = np.tile(np.arange(col+1, dtype=int), (row, 1))
stop = None if unmatch else -1
for i in li:
np.random.shuffle(i[:stop])
return li
else:
def __sshuffle(li):
shuffle(li)
return li
if unmatch:
return [__sshuffle(list(range(col+1))) for i in range(row)]
else:
return [__sshuffle(list(range(col))) + [col+1] for i in range(row)]
この関数は、指定された行数と列数に基づいてランダムな選好表を生成するものである。numpy フラグによって、NumPy配列または通常のリストを生成することができる。また、unmatch フラグによって未マッチング者を示す列を含めるかどうかを制御している。
(h) pseudo_random_preference_table 関数
def pseudo_random_preference_table(row, col, n=1000, **kwargs):
unmatch = kwargs.get('unmatch', True)
if n > row:
n = row
size = col+1 if unmatch else col
sample = np.tile(np.arange(size, dtype=int), (n, 1))
for i in sample:
np.random.shuffle(i)
index = np.random.randint(0, n, row)
li = np.empty((row, size))
li += sample[index]
return li
この関数は、巨大な選好表を擬似ランダムに生成するためのものである。n 個の選好のパターンを用意し、その中からランダムに選んで選好表を生成する。unmatch フラグによって未マッチング者を示す列を含めるかどうかを制御している。
以上が G-Sアルゴリズム実装のコードの概要である。
5.例(シミュレーション)
実際にgale_sharpley関数を実行してみる。
選好表を自分で入力した場合
app_table = [[0, 2, 1, 3], [2, 1, 3, 0], [3, 1, 0, 2]]
hos_table = [[3, 0, 2, 1], [2, 0, 1, 3], [2, 0, 3, 1]]
初めに男性女性がそれぞれ3人の場合を想定して、選好順を上のように作成し実行してみた。
実行結果がこちら
申し込み側からみたマッチングは
[2 1 3]
受け入れ側からみたマッチングは
[3 1 0]
申し込み側から見たマッチングは男性側から見た最適なマッチングを表し、受け入れ側から見たマッチングは女性側から見た最適なマッチングを表している。
これを見ると 0番目の男性は2番目の女性と 1番目の男性は1番目の女性とマッチングし 2番目の男性と0番目の女性は未婚のまま終わったことが分かる。
実際に自分で上の選好順に対して安定マッチングを得ようとしても同じ結果が得られるので、このプログラムは正常に作動しているといえる。
巨大な選好表を作成してもらう
app_table = random_preference_table(1000, 1000)
hos_table = random_preference_table(1000, 1000)
続いて、巨大な人数の男女のマッチングを想定してみる。この場合選好表を自身で生成するのは難しいためrandom_preference_table関数を用いて生成した。まず行数と列数を1000に指定してgale_sharpley関数を実行してみた。
その結果は
申し込み側からみたマッチングは
[ 723 592 442 810 873 357 808 731 307 487 805 1000 185 225
63 634 666 859 286 38 560 380 412 793 441 829 330 1000
951 60 211 119 416 198 1000 962 967 687 705 681 109 409
616 229 825 108 1000 949 36 76 946 880 953 351 794 689
532 714 130 254 832 512 602 383 325 843 4 339 956 413
856 451 720 845 352 429 140 598 238 659 960 772 595 308
348 180 188 645 153 633 1000 585 232 376 904 905 735 1000
959 337 365 599 786 745 427 1000 393 507 915 869 162 908
571 168 1000 813 42 930 265 98 706 724 677 774 626 983
624 518 249 105 31 138 466 345 994 397 399 757 884 594
190 822 885 1000 426 149 91 444 803 842 807 282 111 18
433 562 977 750 635 523 333 72 494 568 902 456 1000 876
812 702 17 925 415 450 806 556 195 606 639 486 950 826
273 809 396 373 597 587 176 612 1000 52 358 614 607 1000
646 846 882 557 3 728 1000 1000 114 262 751 420 156 113
565 491 903 71 77 529 295 1000 758 439 350 828 862 93
75 877 921 214 15 344 692 241 335 652 1000 68 289 305
88 435 233 848 852 654 886 544 340 201 778 841 47 1000
...
611 52 818 452 68 574 792 98 80 482 35 284 304 842
326 36 629 383 887 753 919 683 936 840 252 156 1000 855
988 603 484 125 620 595 780 669 830 453 761 552 797 340
134 954 299 577 339 568]
Output is truncated. View as a scrollable element or open in a text editor. Adjust cell output settings...
省略されてはいるものの、巨大な選好リストをランダムに作成し、安定マッチングを得ることができている。
ちなみに下の2行の英文は、表示領域に収まりきらないということを表している。
つまりそれほど巨大な数に対しても正しく動いてくれている。なんと心強い性能だ!
また選好表を作成するのにかかった時間は1.199481725692749 秒で、その選好表をもとにマッチングを得るのにかかった時間は0.47449469566345215 秒だった(どちらも複数回実行すると多少の誤差が生まれる)。始めの男女3人ずつで実行した場合は0.0秒(としか表示されなかった)で結果が得られたことと比較するとかなりの時間がかかっていることが分かる。
ここで行数と列数を2000に指定して実行してみると
選好表生成は 4.650441646575928 秒かかっていて、データが4倍に増えたのに対して時間もほぼ4倍になっている。しかし実行時間は 1.2495336532592773 秒と、選好表生成に比べてかかる時間はあまり増えていない。
このことからPythonにとってはこの程度の複雑さを持つ関数を実行することは、巨大な行列を生成することよりもかなり簡単な作業であるといえる。
上の「4.実装」では、巨大な人数の選好表生成するために選好パターンを複数個生成しその中からランダムに選んで選好表を生成する pseudo_random_preference_table 関数があったことを思い出そう。次はこの関数を用いて巨大な人数分の選好表を用意しgale_sharpley関数を実行してみた。
まずは行列数をそれぞれ1000に指定した。
random_preference_table 関数を用いた時と同じように正常なマッチングが返されたのだが、注目すべきはその実行時間である。選好表生成にかかった時間は0.20723247528076172秒で、マッチングの実行時間は0.14473390579223633秒だった。
どちらも random_preference_table 関数を用いた時と比べ大幅な時間短縮ができた。
続いて、行列数をそれぞれ2000に指定してみた。
選好表生成は0.34415769577026367秒、マッチングの実行時間は0.6246931552886963秒だった。両方を合わせた時間は random_preference_table 関数を用いた時と比較して約6分の1まで短縮することができた!

2つの関数の比較
やはり巨大な人数分の選好表を生成するときは 、pseudo_random_preference_table 関数を用いて選好表を生成した方が時間が短縮されて良い。では、2つの関数で実行した場合、行列の大きさがどれくらいだと時間の差が生まれてくるのだろうか?また行列が小さい場合は pseudo_random_preference_table 関数を使用した方が時間がかかることはあるのだろうか?
2つの関数の行列数を0~999にそれぞれ指定して実行してみた。以下はその処理時間を表にしたものである。x軸は選好表のサイズ、y軸は表の生成時間を表している。
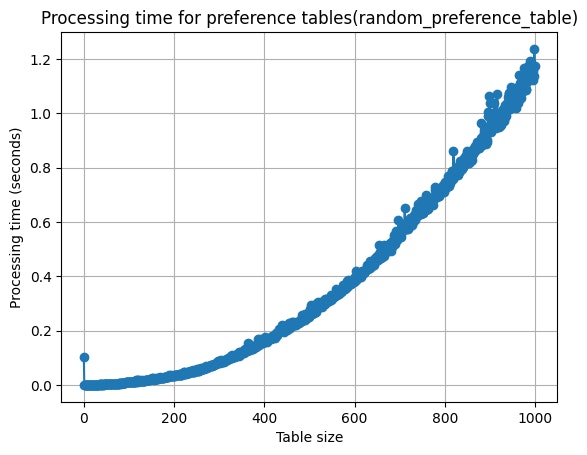
random_preference_table 関数を使用した場合、グラフはきれいな曲線を描いている。気になることは表のサイズが700以上になると曲線から浮いたプロットが目立ち始めることだ。900台ではプロットが離れ離れになっており、ここまでくると選好表の生成処理が難しくなってきていることが分かる。
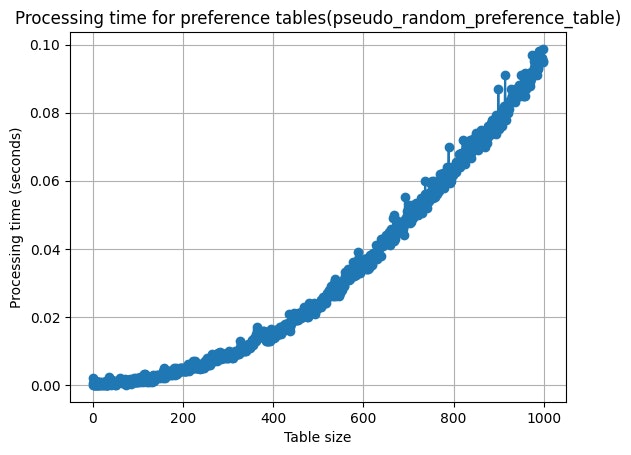
一方 psuedo_random_preference_table 関数を使用した時もグラフの後半になるにつれてプロットが離れ離れになる傾向があるが、先のグラフと比べるとその差は小さいといえる。
また生成時間を2つのグラフで比べてみる。時間が0.10秒に達した表のサイズは random_preference_table 関数では300付近、psuedo_random_preference_table 関数では1000付近と大きな差が出た。どの表のサイズをとっても psuedo_random_preference_table 関数の方が生成時間は短かった。
しかし筆者が実行を繰り返したところ表のサイズが100付近までは、同じサイズの表の生成でっても生成時間にぶれが生まれやすく、その傾向は psuedo_random_preference_table関数を使用した時の方が大きかった。よって100付近までは random_preference_table 関数、それ以降は psuedo_random_preference_table 関数を使用した方がいいかもしれない。
6.課題 応用
ここではG-Sアルゴリズムの応用と課題について説明していく。いままで男性と女性の数が等しい場合でG-Sアルゴリズムについて説明してきたが、これは男女の数が異なる場合でも成り立つ。男性が6人、女性が3人の場合の安定マッチングについて以下の図で説明する。
人数比が異なる場合流れは本質的には同じであるため、成立する。
次に課題について説明していく。まずは計算量的な困難性である。
応募者と受け入れる側がそれぞれn人の場合、安定マッチングが終了するまでに一連のアルゴリズムを最大でn^2回繰り返すことになる。よってnの数が大きいと試行回数が大きすぎて計算が困難になる場合がある。
二つ目の課題は安定結婚問題にG-Sアルゴリズムを用いる場合、男性側がプロポーズする場合は男性側にとっては選好順がある程度適用されるが、女性側にとっては好まない組み合わせになる場合が多い。女性側がプロポーズする場合は逆になる。
(例)男性二人と女性二人のマッチングの簡単な例で説明する。
男X、Yと女A、Bの二人ずつでマッチングをする場合を考える。
選好表がそれぞれXがA>B、YがB>A、AがY>X 、BがX>Yであると仮定。
男性側からアルゴリズムを動かすと(X,A)、(Y,B)のペアが生まれる。これは男性にとってはどちらも最高のパートナーであるため安定マッチングだが、女性にとってはどちらも第二候補のパートナーとなる。逆に女性が申し込む側にすると(A,Y)、(B,X)のペアになり、こちらも安定している。このようにどちら側がプロポーズするかによってマッチングのペアが変わるし、プロポーズする側の選好が反映されやすくなる。
三つ目の課題として、選考基準が複数ある場合である。結婚問題であれば人それぞれ異なる基準があり、どれを優先するかも異なる。そのためどの基準を優先するかが問題となる。
7.まとめ
G-Sアルゴリズムは、マッチング問題において安定なパートナーシップを求める優れた手法である。本ブログでは、その基本概念から実装、シミュレーションまでを詳細に解説した。アルゴリズムは応募者が最適な相手に提案し、断られた場合は順位次に進む仕組みとなっている。これにより、安定かつ効率的なマッチングが可能となり、医療や進学など多岐にわたる分野で活用されている。また、実装例では大規模なデータセットにも対応可能であるが、計算量の増大や異なる基準の取り扱いといった課題もある。