0.結論
pythonでプロ野球投手の年俸に最も影響を及ぼす要因を調べてみた。
結論として影響したのが、投げた回数や年齢。
意外と投手として「流した汗」に直結しているデータが上位を来た。
逆に、投手から見ればカッコ良い奪三振が下位なのにはビックリした。
1.背景・経緯
プロ野球には一般的なレベルで興味がある。何億も稼ぐ選手がいる一方で、金銭的に恵まれない選手もいる。年俸が何で決まるのか、調べてみることにした。
事前の予想では、勝ち星の数や奪三振が年俸に影響を与えそう。何年もやっている年齢が上の選手が稼いでいるのかもしれない。
2.データの準備
何は無くともデータの準備。データは「プロ野球データFreak」さんから、お借りしました。とても良くデータがまとまっていて、大変、助かりました。この場を借りて、御礼を申し上げます。
http://baseball-data.com/
データ分析の前段階が、一番、手間がかかる。今回はexcelを駆使して、データ分析の前作業をした。ここが一番、時間が掛かった。
今回は2017年度の投手の年俸と各種成績(注)等との関係を見た。
(注)防御率、試合、勝利、敗北、セーブ、ホールド、勝率、、打者、投球回、被安打、被本塁打、与四球、与死球、奪三振、失点、自責点、WHIP、DIPS
ちなみに、~~投球回は1/3回、2/3回が正しいけど、元のデータが.1、.2となっているので、そのまま、使用した。~~投球回は1/3回、2/3回を手補正した。
(参考)以下の指標は初めて知った。
WHIP:Walks plus Hits per Inning Pitched、「投球回あたり与四球・被安打数合計」 ⇒1投球回あたり何人の走者を出したかを表す数値
DIPS:Defense Independent Pitching Statistics、守備の影響とは独立に投手の成績を評価するという概念及びその評価手法 ⇒投手のみに責任がある要素である奪三振、与四球、被本塁打から投手を評価
また、プロ野球で何年活躍しているかや、年齢も年俸に影響を与えそうだから、重回帰分析をするときは要因として考えてみた。
なお、年俸は当然のことながら推定値だし、不明な場合は分析の対象外とした。データ分析の際、NA値は平均値などで置き換えることも多いけど、今回は対象外とするのが適当だ。
【重要な修正】
二重共線性ありとの指摘を受け、分析対象とするデータを一部、削除しました。
(修正前)
防御率、試合、勝利、敗北、セーブ、ホールド、勝率、打者、投球回、被安打、被本塁打、与四球、与死球、奪三振、失点、自責点、WHIP、DIPS、年数、年齢、年俸
(修正後)
勝利、敗北、セーブ、ホールド、投球回、被安打(被安打からは被本塁打を除いて計算)、被本塁打、与四死球(与四球と与死球の合計)、奪三振、自責点、年齢、年俸
ご指摘を頂きましたyueno様、ありがとうございました。
この場を借りて、御礼を申し上げます。
3.データ読み込み
pythonはjupyterを使う。まずは、pandasとnumpyをimport。
データ(baseball_pitcher1.csv)は事前に準備しておいた。データはutf-8で保存しておく必要がある。jupyterを起動したのと同じフォルダに格納しておこう。
なお、データ分析手法は「Python でデータサイエンス」さんを参考にさせて頂きました。良質で、大変、良いサイトだと思います。この場を借りて、御礼を申し上げます。
https://pythondatascience.plavox.info/
import pandas as pd
import numpy as np
baseball_pitcher = pd.read_csv("baseball_pitcher3.csv", sep=",")
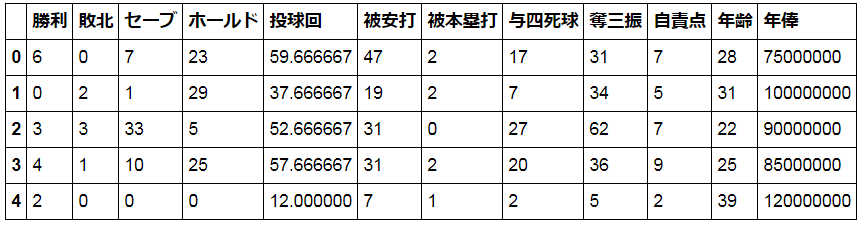
baseball_pitcher.head()# 被安打は被本塁打を含まない
ちなみに、データサイズは以下の通り。
baseball_pitcher.shape
(100, 12)
年俸が分かる投手100名のみを分析対象とした。
4.単回帰分析
まずは、小手調べとして投手の勝ち星と年俸との関係を見てみよう。これは単回帰分析となる。分析にはsklearnを使った。
# sklearn.linear_model.LinearRegression クラスを読み込み
from sklearn import linear_model
clf = linear_model.LinearRegression()
# 説明変数に "勝利" を利用
X = baseball_pitcher.loc[:, ['勝利']].as_matrix()
# 目的変数に "年俸" を利用
Y = baseball_pitcher['年俸'].as_matrix()
# 予測モデルを作成
clf.fit(X, Y)
# 回帰係数
print(clf.coef_)
# 切片 (誤差)
print(clf.intercept_)
# 決定係数
print(clf.score(X, Y))
結果は、
[ 7138804.8723838]
102971004.413
0.0930072283462
これだけだと良く分らないので、グラフ化してみよう。
# matplotlib inline
# matplotlib パッケージを読み込み
import matplotlib.pyplot as plt
# 散布図
plt.scatter(X, Y)
# 回帰直線
plt.plot(X, clf.predict(X))
plt.show()
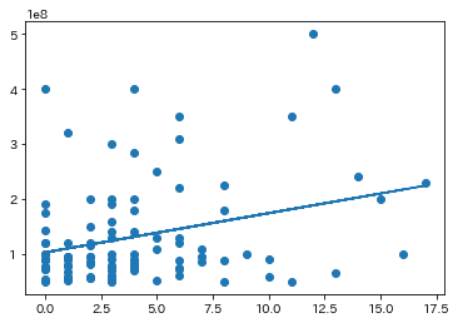
回帰直線は、かろうじて右肩上がり。
まあ、右肩上がりになるのは、当たり前か。
5.重回帰分析
さて、いよいよ、年俸が何で決まるか、見てみよう。
まずは、正規化を実行しよう。
正規化には主に2つの手法がある。
1.最大値を 1、最小値を 0 にする正規化
2.平均を 0、分散を 1 にする正規化
ここでは、後者を使うことにする。
なお、正規化については、以下の記事が大変、参考になります。
https://mathwords.net/dataseikika
この場を借りて、御礼を申し上げます。
from sklearn import linear_model
clf = linear_model.LinearRegression()
# データフレームの各列を正規化
# 不偏標準偏差を使用(yueno様、ありがとうございました)
baseball_pitcher2 = baseball_pitcher.apply(lambda x: (x - np.mean(x)) / np.std(x,ddof=1))
baseball_pitcher2.head()
それでは、分析してみよう。
年俸以外を説明変数とし、年俸を目的変数として、分析してみよう。
# 説明変数に "年俸以外すべて" を利用
baseball_pitcher2_except_money = baseball_pitcher2.drop("年俸", axis=1)
X = baseball_pitcher2_except_money.as_matrix()
# 目的変数に "年俸" を利用
Y = baseball_pitcher2['年俸'].as_matrix()
# 予測モデルを作成
clf.fit(X, Y)
# 偏回帰係数
print(pd.DataFrame({"Name":baseball_pitcher2_except_money.columns,
"Coefficients":np.abs(clf.coef_)}).sort_values(by='Coefficients') )
# 切片 (誤差)
print(clf.intercept_)
結果は、以下の通り。
Coefficients Name
7 0.056618 与四死球
8 0.056725 奪三振
1 0.065737 敗北
2 0.107369 セーブ
3 0.167422 ホールド
9 0.167978 自責点
0 0.197051 勝利
6 0.227691 被本塁打
5 0.437383 被安打
10 0.439686 年齢
4 0.571961 投球回
-1.42532102836e-16
結果から分かるように、年俸に影響があるのは、対戦した打者数や投球回数となる。打者数と投球回数は同じような指標なので、どちらか一方のみを採用しても良いのかもしれない。年齢が、その次なのは、プロで生き残った結果が蓄積されたという解釈しても良いのかな。敗北や自責点が下位にくるのは分かるけど、勝率や防御率が下位なのは意外な感じがする。
結果から分かるように、年俸に影響があるのは、投球回や年齢。投球回は汗の象徴。年齢も過去からの汗の結晶(?)かもしれない。
被安打や被本塁打、自責点は投球回が多くなれば、当然、多くなるということか。
与四死球や敗北が下位に来るのは分かるけど、奪三振が下位なのは意外な感じがする。
データ分析を勉強するのは面白い。いろいろ、分析してみよう。
最後に
バッター編も作ってみました。
もし、良ければ、こちらをご覧ください。