はじめに
本記事は、前回(ピッチャー編)の続きです。![]()
前回は、こちらになります。
0.結論
今回は、pythonで打者の年俸に最も影響を及ぼす要因を調べてみた。
結論としては、最も影響したのが、意外にも打数![]()
それから、当然のように安打や四死球、本塁打が上位になった。
投手同様、まずは使ってもらってナンボの世界だね。
大切なのは信頼を勝ち取るということかな。
1.背景・経緯
前回、ピッチャーの年俸に影響している要因を調べた。
今回は、バッターの年俸に影響している要因を調べてみたい。もっとも、因果関係と言うより、相関関係と言った方が正確かもしれない。
いずれにせよ、個人的にデータ分析してみたら、こんなでしたよ、面白いね、といった安直なレベルで書いているので、寛大に読んで頂ければ有り難い。
もちろん、自分の勉強になるので、突っ込んで頂くのは歓迎です(笑)
事前の予想では、何と言っても、安打数かな?
出塁率を上げる四死球なんていうのも意外と貢献していそう。
2.データの準備
今回も、データは「プロ野球データFreak」さんから、お借りしました。とても良くデータがまとまっていて、大変、助かりました。この場を借りて、御礼を申し上げます。
http://baseball-data.com/
毎度、データ分析の前段階が、一番、手間がかかる。今回もexcelを駆使して、データ分析の前作業をした。
今回は、前回の反省を踏まえ、事前にデータの要・不要を吟味した。
「プロ野球データFreak」さんで提供して頂いているデータは以下の通り。守備に関するデータ(守備機会やエラー数など)が無いのが残念だが、データの種類としては多い。
【使用可能な打者関連データ】
打率、試合、打席数、打数、安打、本塁打、打点、盗塁、四球、死球、三振、犠打、併殺打、長打率、出塁率、OPS、RC27、XR27
この内、以下は知らないので調べてみた。
OPS(On-base plus slugging)は、出塁率+長打率。
RC27(Runs Created per 27 outs)とXR27(eXtrapolated Runs per 27 outs)は、ともに特定の選手1人で構成された打線で試合を行った場合、27アウト(9イニング×3アウト=1試合)で平均何点とれるかを算出した指標だけど、XRは「安打を単打、二塁打、三塁打、本塁打に区別」「四球と故意四球(敬遠)を区別」して計算している。
【使用したデータ】
打数、安打、本塁打、打点、盗塁、四死球、三振、犠打、併殺打、年齢、年俸
使用したデータは上記の通り。
前回の轍を踏まえ、多重共線性(マルチコ)が発生しないようにデータ内容が重ならないように選んだ(つもり)![]()
四死球は四球と死球の合計。
安打は本来、本塁打を含むけど、ダブルカウントになるので、本塁打を引いて計算した。
打者関連のデータではないけど、年齢は前年までの蓄積を表す意味でも入れておいた。
年俸は、当然のことながら、目的変数で、他が説明変数。年俸が不明な選手のデータは分析が出来ないので、対象外とした。
3.データ読み込み
前回同様、pythonはjupyterを使う。まずは、pandasとnumpyをimport。
データ(baseball_batter.csv)は事前に準備しておいた。データはutf-8で保存しておく必要がある。jupyterを起動したのと同じフォルダに格納しておこう。
import pandas as pd
import numpy as np
baseball_batter = pd.read_csv("baseball_batter.csv", sep=",")
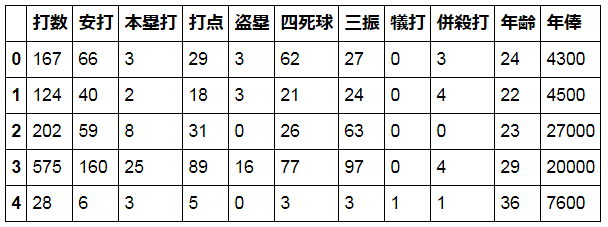
baseball_batter.head()
ちなみに、データサイズは以下の通り。
baseball_batter.shape
(99, 11)
年俸と成績が分かる99名のみを分析対象とした。
ちなみに、当然のことながら、大谷翔平選手も対象に入っています![]()
4.単回帰分析
まずは、小手調べとして安打数と年俸との関係を見てみよう。これは単回帰分析となる。分析にはsklearnを使った。
# sklearn.linear_model.LinearRegression クラスを読み込み
from sklearn import linear_model
clf = linear_model.LinearRegression()
# 説明変数に "安打" を利用
X = baseball_batter.loc[:, ['安打']].as_matrix()
# 目的変数に "年俸" を利用
Y = baseball_batter['年俸'].as_matrix()
# 予測モデルを作成
clf.fit(X, Y)
# 回帰係数
print(clf.coef_)
# 切片 (誤差)
print(clf.intercept_)
# 決定係数
print(clf.score(X, Y))
結果は、
[ 67.70699197]
9656.60146082
0.0822971621313
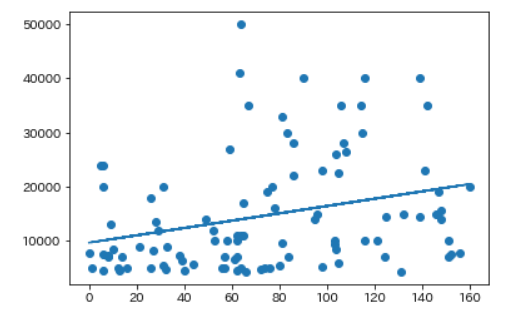
これだけだと良く分らないので、グラフ化してみよう。
# matplotlib inline
# matplotlib パッケージを読み込み
import matplotlib.pyplot as plt
# 散布図
plt.scatter(X, Y)
# 回帰直線
plt.plot(X, clf.predict(X))
plt.show()
回帰直線は、前回同様、かろうじて右肩上がり。
もっと右肩上がりになると思ったのだけど、これは意外![]()
5.重回帰分析
さて、いよいよ、年俸が何で決まるか、見てみよう。
まずは、正規化を実行しよう。
正規化には 、前回同様、「平均を0、分散を 1 にする正規化」を使う。
from sklearn import linear_model
clf = linear_model.LinearRegression()
# データフレームの各列を正規化
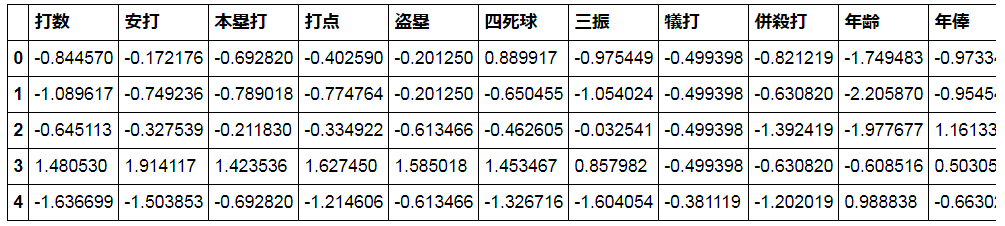
baseball_batter2 = baseball_batter.apply(lambda x: (x - np.mean(x)) / np.std(x,ddof=1))
baseball_batter2.head()
それでは、分析してみよう。
年俸以外を説明変数とし、年俸を目的変数として、分析してみよう。
# 説明変数に "年俸以外すべて" を利用
baseball_batter2_except_money = baseball_batter2.drop("年俸", axis=1)
X = baseball_batter2_except_money.as_matrix()
# 目的変数に "年俸" を利用
Y = baseball_batter2['年俸'].as_matrix()
# 予測モデルを作成
clf.fit(X, Y)
# 偏回帰係数
print(pd.DataFrame({"Name":baseball_batter2_except_money.columns,
"Coefficients":np.abs(clf.coef_)}).sort_values(by='Coefficients') )
# 切片 (誤差)
print(clf.intercept_)
結果は、以下の通り。
Coefficients Name
4 0.022832 盗塁
3 0.026300 打点
8 0.128289 併殺打
7 0.138566 犠打
9 0.161844 年齢
6 0.204712 三振
2 0.216191 本塁打
5 0.247341 四死球
1 0.568593 安打
0 0.698359 打数
2.49232875356e-17
結果から分かるように、年俸に最も影響があるのは、なんと、打数![]()
どれだけ、打席に立つかが、本当に大事なんだね。
安打や四死球、本塁打も、当然のごとく、上位を占めている。
ランナーの有無が影響する打点が下位なのは分かる気もするけど、盗塁が下位なのはビックリ![]()
監督からの指示が出れば、盗塁するけど、このデータを見る限りでは、盗塁王を争うような選手じゃないと、盗塁してもイマイチかな。まあ、俊足を売りにする選手なら、やっても良いね。要は自分のセールスポイントを何にするかかな。
データ分析を使ってみるのは面白い。いろいろ、分析してみよう。