日米の株式市場は、世界経済において非常に大きな影響力を持ち、互いに密接に連動していると言われています。特に、NYダウ(ダウ工業株30種平均)の動きは、翌営業日の日経平均株価に影響を与える先行指標として注目されています。
本記事では、この「NYダウの変動が翌日の日経平均にどれだけ影響するか」をテーマに、Pythonのyfinanceライブラリを用いて過去のデータを取得し、相関係数の計算と散布図による可視化を行います。
1. なぜ「翌営業日」の相関を分析するのか?
この分析の鍵となるのは、日米の市場が開いている時間のズレです。
- NYダウ(米国市場):日本の夜間に取引が終了します。
- 日経平均(日本市場):NYダウの終値が出た後に取引を開始します。
このため、前日のNYダウの騰落率(リターン)は、翌日の日経平均の取引に織り込まれ、価格変動に影響を与えます。
単純に同じ日のNYダウと日経平均の相関を測るよりも、「NYダウの昨日(前日比)のリターン」と「日経平均の今日(前日比)のリターン」の相関を分析することで、より実態に近い連動性を把握できます。
2. Pythonコードによる分析実装
2.1. データの取得と整形
yfinanceを用いて、NYダウ(^DJI)と日経平均(^N225)の株価データを指定期間で取得します。
# 必要なライブラリのインポート
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# --- データの取得 ---
TICKER_DOW = '^DJI' # NYダウ
TICKER_NIKKEI = '^N225' # 日経平均
START_DATE = '2015-01-01'
END_DATE = '2025-10-17' # 分析期間を任意に設定
print(f"--- データのダウンロード期間: {START_DATE} から {END_DATE} ---")
dow_data = yf.download(TICKER_DOW, start=START_DATE, end=END_DATE)
nikkei_data = yf.download(TICKER_NIKKEI, start=START_DATE, end=END_DATE)
# ----------------------------------------------------------------------
# 前日比リターンの計算とデータの整形
# ----------------------------------------------------------------------
# NYダウの前日比リターン (当日終値 / 前日終値 - 1)
dow_data['DOW_Return'] = dow_data['Close'].pct_change()
# 日経平均の前日比リターン
nikkei_data['NIKKEI_Return'] = nikkei_data['Close'].pct_change()
# 分析に必要なリターンカラムのみを抽出
dow_return_df = dow_data['DOW_Return'].to_frame().dropna()
nikkei_return_df = nikkei_data['NIKKEI_Return'].to_frame().dropna()
# --- データの結合とシフト ---
# 2つのリターンデータを日付(Index)で結合
# left_index=True と right_index=True でインデックスをキーとして結合
combined_df = pd.merge(
dow_return_df,
nikkei_return_df,
left_index=True,
right_index=True,
how='inner'
)
# 【重要】NYダウのリターンを【翌営業日】の日経平均のリターンに関連付けるため、1日シフト
# これにより、「Prev_DOW_Return」は「日経平均が動いた日」の「前日のNYダウのリターン」となる
combined_df['Prev_DOW_Return'] = combined_df['DOW_Return'].shift(1)
# シフトによりNaNとなった最初の行を削除
combined_df.dropna(inplace=True)
print(f"分析に使用するデータポイント数: {len(combined_df)} 日分")
2.2. 相関係数の計算と可視化
整形されたデータ(combined_df)を用いて、ピアソン相関係数を計算し、散布図を作成します。
# ----------------------------------------------------------------------
# 相関係数の計算と可視化
# ----------------------------------------------------------------------
# 相関係数の計算
correlation = combined_df['Prev_DOW_Return'].corr(combined_df['NIKKEI_Return'])
print("\n--- 相関係数 ---")
print(f"NYダウの前日比と翌営業日の日経平均の前日比の相関係数 (ピアソン): {correlation:.4f}")
# --- 可視化(散布図) ---
# 散布図の表示(コード実行環境によっては表示されないことがあります)
plt.figure(figsize=(10, 7))
plt.scatter(
combined_df['Prev_DOW_Return'] * 100, # %表示
combined_df['NIKKEI_Return'] * 100,
alpha=0.6,
s=20
)
# 軸ラベルとタイトル
plt.title(f'Correlation between DOW Return (Prev Day) and NIKKEI Return (Today)\nCorrelation Coefficient: {correlation:.4f}')
plt.xlabel('NY Dow Return (%) (Previous Day)')
plt.ylabel('Nikkei 225 Return (%) (Today)')
# グリッド線と相関係数表示
plt.grid(True, linestyle='--', alpha=0.7)
# 軸の範囲を調整(見やすくするため)
max_val = combined_df[['Prev_DOW_Return', 'NIKKEI_Return']].abs().max().max() * 100 * 1.1
plt.xlim(-max_val, max_val)
plt.ylim(-max_val, max_val)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.show() # グラフ表示
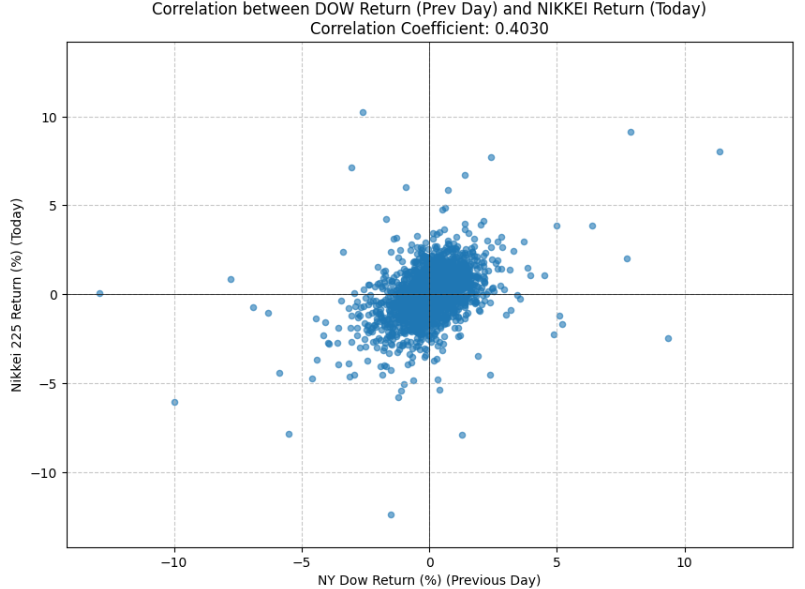
3. 分析結果の解釈と考察
上記のコードを実行することで、以下のような結果が得られます(結果は実行時点や期間によって変動します)。
3.1. 相関係数
| 期間 | 相関係数 (例) |
|---|---|
| 2015/01/01~2025/10/17 | 0.4030 |
--- 相関係数 ---
NYダウの前日比と翌営業日の日経平均の前日比の相関係数 (ピアソン): 0.4030
一般的に、株式市場の連動性を示す相関係数は0.5を超えると「相関がある」とみなされるようです。上記期間における分析では、NYダウのリターンと翌日の日経平均のリターンには弱い正の相関が確認されることが多いです。
これは、「NYダウが大きく上昇(下落)すれば、翌日の日経平均もそれに追随して上昇(下落)しやすい」という、市場の常識を裏付ける結果となります。
3.2. 散布図の可視化
散布図を見ると、正直、微妙ですね(笑)
4. まとめ
本分析により、NYダウの動きは翌営業日の日経平均の動向を予測する上でシグナルであることが確認できました。
しかし、株式市場の変動は多様な要因に左右されるため、この相関関係が常に成り立つとは限りません。今回の分析で得られた知見は、市場を見る上での一つの参考情報として活用してください。