はじめに
AtCoderのコンテストに参加したところ、排他的論理和の問題が出てきました。
基本的なことは知っていましたが、知らない性質もあったので、
今回は排他的論理和について書きたいと思います。
排他的論理和とは
ビット演算などにおいて、2つの入力のどちらかが真でもう片方が偽の時に結果が真になり、
両方とも真、あるいは偽の時に結果が偽になる演算です。演算子は⊻や⊕で表示されます。
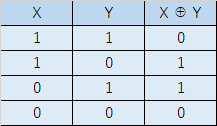
真理値表を見ると分かりやすいのですね。真が1、偽が0です。
pythonでも動かしてみましょう。
pythonでの演算子は"^"です。
test.py
print(1 ^ 1)
print(1 ^ 0)
print(0 ^ 1)
print(0 ^ 0)
実行
$ python test.py
0
1
1
0
排他的論理和の性質
排他的論理和には、いくつか性質があります。
x ^ y == y ^ x
(x ^ y) ^ z == x ^ (y ^ z)
交換則、結合則が成立します。また、
x ^ x == 0
x ^ 0 == x
x ^ y ^ y == x
なども成立します。
自分自身でXORすると0になる法則は、多くのプロセッサでレジスタをゼロクリアするときに使われるそうです。
どうやら直接0を書き込むよりも早いらしい。
同じビットで2回XORすると元に戻る法則は様々な応用があり、単純なものでは、「XOR交換アルゴリズム」や「XOR連結リスト」、ｙを鍵として暗号化などが出来るそうです。
実際に「XOR交換アルゴリズム」をpythonで書いてみると、
test.py
x = 3
y = 7
print(x, y)
x = x ^ y
y = x ^ y
x = x ^ y
print(x, y)
実行
$ python test.py
3 7
7 3
うまく出来ていますね。
まとめ
同じビットで2回XORすると元に戻る法則は重要そうですね。
覚えておきたいです。