C#.NetのMathクラスとComplexクラスの違いまとめ(使用例付き)
普段C#で数値計算をしていると、
「このケースはMathで計算できるのか?」「Complexを使わないといけないのか?」
と迷うことがあるかと思います。
特に平方根や対数に負の値が入ったときに違いがはっきり出ます。
この記事ではMathクラスとComplexクラスの違いを表形式で整理し、使用例もまとめてみました。
1. Math と Complex の基本的な違い
-
Math
- 実数専用(double精度)
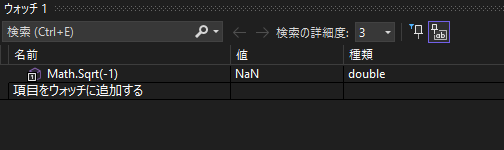
- 負の数の平方根や対数は計算できず
NaNを返す - 高速・軽量
-
Complex
-
System.Numerics.Complex構造体 - 実数だけでなく虚数も扱える
-
Mathでは落ちる計算も正しく複素数として結果を返す
-
2.主なメソッド比較表
| 関数 | Math | Complex |
|---|---|---|
| 平方根 √ |
Math.Sqrt(4) = 2Math.Sqrt(-1) = NaN
|
Complex.Sqrt(4) = (2, 0)Complex.Sqrt(-1) = (0, 1)
|
| 指数 e^x | Math.Exp(1) ≈ 2.718 |
Complex.Exp(iπ) = -1 |
| 自然対数 ln |
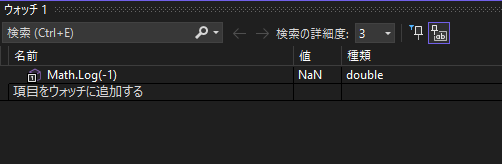
Math.Log(10) ≈ 2.302Math.Log(-1) = NaN
|
Complex.Log(-1) = (0, π) |
| 常用対数 log10 | Math.Log10(100) = 2 |
Complex.Log10(-100) = (2, πi / ln(10)) |
| 三角関数 sin | Math.Sin(π/2) = 1 |
Complex.Sin(i) ≈ (0, 1.175) |
| 三角関数 cos | Math.Cos(0) = 1 |
Complex.Cos(i) ≈ (1.543, 0) |
| tan | Math.Tan(π/4) = 1 |
Complex.Tan(i) ≈ (0, 0.7616) |
3.使用例
使用例で示している画像はVisualStudioのウォッチとなります。
負の数の平方根
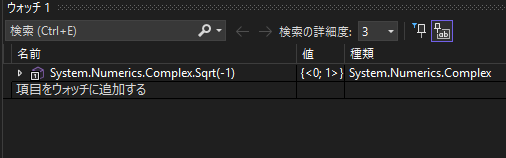
※<>の中の第1引数が実数部、第2引数が虚数部となります。
ですので、√-1 = i という解が得られます。
負の数の対数
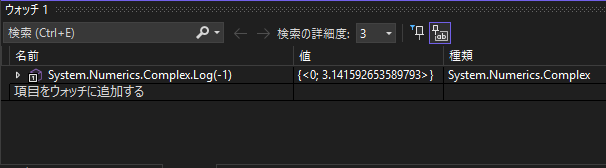
log(-1)=iπになるというのは、オイラーの等式e^iπ+1=0から導くことが出来ます。
とは言ってもやることは、1を右辺に移項して自然対数を取るだけなのですが。
オイラーの等式
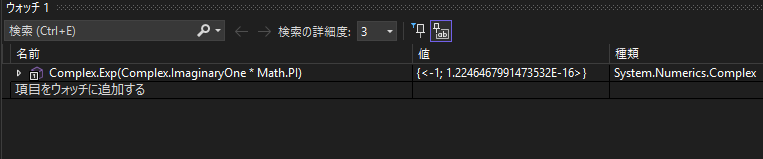
e^iπの解の実部が-1となっています。
虚部に値が出てくるのは、本来無理数で定義されるeとπが言語やライブラリによって有理数に丸め込まれているため誤差としてあらわれます。
ですので、実際に使用するときは丸める必要があるということになります。
4.まとめ
- 実数だけならMathクラスで十分
- 負の数や複素数を含むならComplexクラスが必須
- 使い分けを理解しておくとNaNやエラーを避けられる
5.実用例:S-Calc
この記事で紹介したような
「MathではNaNになるケースをComplexを使って解く」
処理を取り入れた関数電卓ソフトS-Calcを個人開発しています。
-
log(-5)のような複素数対数の計算 - sin,cos,tanなどの度数法/弧度法切替
- arcsin,arccos,arctanなどの解を度数法/弧度法どちらで取得するかの切り替え
- 虚数を含めた計算
など、普通の電卓では扱えない計算にも対応しています。
📺 関連動画
普通の電卓では計算できない log(-5), ln(-1), √(-9) なども解ける
Windows向け関数電卓ソフト「S-Calc」の紹介動画を公開しました。
👉 興味のある方は Microsoft Store からぜひご利用ください。
S-Calc in MicrosoftStore
この記事が役に立ったと思ったら、LGTM 👍 やフォローをしていただけると励みになります!