逆数平方根の収束公式と丸め誤差

はじめに

逆数平方根の計算を近似値から精度改善する公式は以下のようになります．

\begin{aligned}
y_0 \sim& 1 / \sqrt{x} \\
h  = & 1- xy_0^2 \\
y_1 =& y_0 \left(1 + \frac12 h + \frac38 h^2 + \frac5{16} h^3 + \cdots \right)
\end{aligned}

$()$の中は，$(1-h)^{-1/2}$のテイラー展開となっています．
Maximaに係数を計算してもらうには，

(%i1) taylor((1-h)^(-1/2), h, 0, 5);

のように書きます．
これをソースコードに落とし込んで実装するにあたっては，何次の公式を何回適用するのかも大事なのですが，最後の1回に関しては丸め誤差の影響が小さくて済むかたちを考えなくてはなりません．

近似計算

今回は丸め誤差の影響を見ていきたいので，単精度に限って計算することにします（誤差の評価のみを倍精度で行う）．
近似の初期値計算としては，以下
https://en.wikipedia.org/wiki/Fast_inverse_square_root
でよく知られているものを用います．

static inline float rsqrtf_app(float x){
    union{
        float f;
        int   i;
    }m32;
    m32.f = x;
    m32.i = 0x5f3759df - (m32.i >> 1);

    return m32.f;
}

浮動小数点のデータに対して整数演算を行うとは随分と野蛮ですが，これで有効桁数が2進数にして4-bit程度の近似が可能です．通常のNewton法（多項式の$h$の次数までを評価）の場合は有効桁数が倍々になっていくので仮数部が24-bitの単精度までなら3回適用すればよいものと思われます．$\frac38 h^2$の項まで評価した場合，有効桁数は3倍になっていくので2回適用すればいいでしょう．
2倍公式の実装は2種類を作ってみました．

static inline float conv_2nd_A(float x, float y){
    float p = 1.5f - (0.5f*x) * (y * y);
    float ret = y * p;
    return ret;
}

static inline float conv_2nd_B(float x, float y){
    float hh = 0.5f - (0.5f*x) * (y * y);
    float ret =  __builtin_fmaf(y, hh, y);
    return ret;
}

fmaf(x, y, z)はx * y + zを計算します．Fusedな積和になっているかどうかはここではまだあまり問題ではありません¹．ふたつの実装の大きな違いは，前者（A）が

y_1 = \left( 1 + \frac12 h \right) y_0

のように補正多項式を計算して下の方の桁が丸まってしまったものを近似値に対して掛けているのに対して，後者（B）では

y_1 = y_0  + \left( \frac12 h \right) y_0

のようにオリジナルの値に対して小さな補正値を計算してこれを足し込むという実装になっていることです．
同様に3倍公式も2種類作ってみました：

static inline float conv_3rd_A(float x, float y){
    float h = 1.f - x * (y * y);
    float poly = 1.0f + h * (0.5f + h * 0.375f);
    float ret =  y * poly;
    return ret;
}

static inline float conv_3rd_B(float x, float y){
    float h = 1.f - x * (y * y);
    float poly = h * (0.5f + h * 0.375f);
    float ret =  __builtin_fmaf(y, poly, y);
    return ret;
}

#誤差の計測
入力値は，[1.0, 4.0)の区間になるように

    float x = float(pow(4.0, drand48()));

で作ってあります．
倍精度で計算したものとの相対誤差は，

static double err_rsqrt(float xf, float yf){
    double x = xf;
    double err = sqrt(x) * (yf - 1.0/sqrt(x)) ;
    return err;
}

のように計算してあります．

MacでFMAを有効にしてコンパイルするのは少し大変で，OS（筆者の環境はEl Capitan）付属のアセンブラが古く，FMAというかAVXをコンパイルしてくれません．MacPorts等由来のg++の場合，アセンブラにのみclangを使うというオプションが使えたので，

g++ -O2 -Wall -mfma -Wa,-q --std=c++11

としました．GNU方言の酷くないコードなら，clang++を使うのも可能です²．

とりあえずサンプル数を65536個で誤差の分布を見てみたのが，以下の図になります（単にソートしてプロットしているので横軸は割合です）．

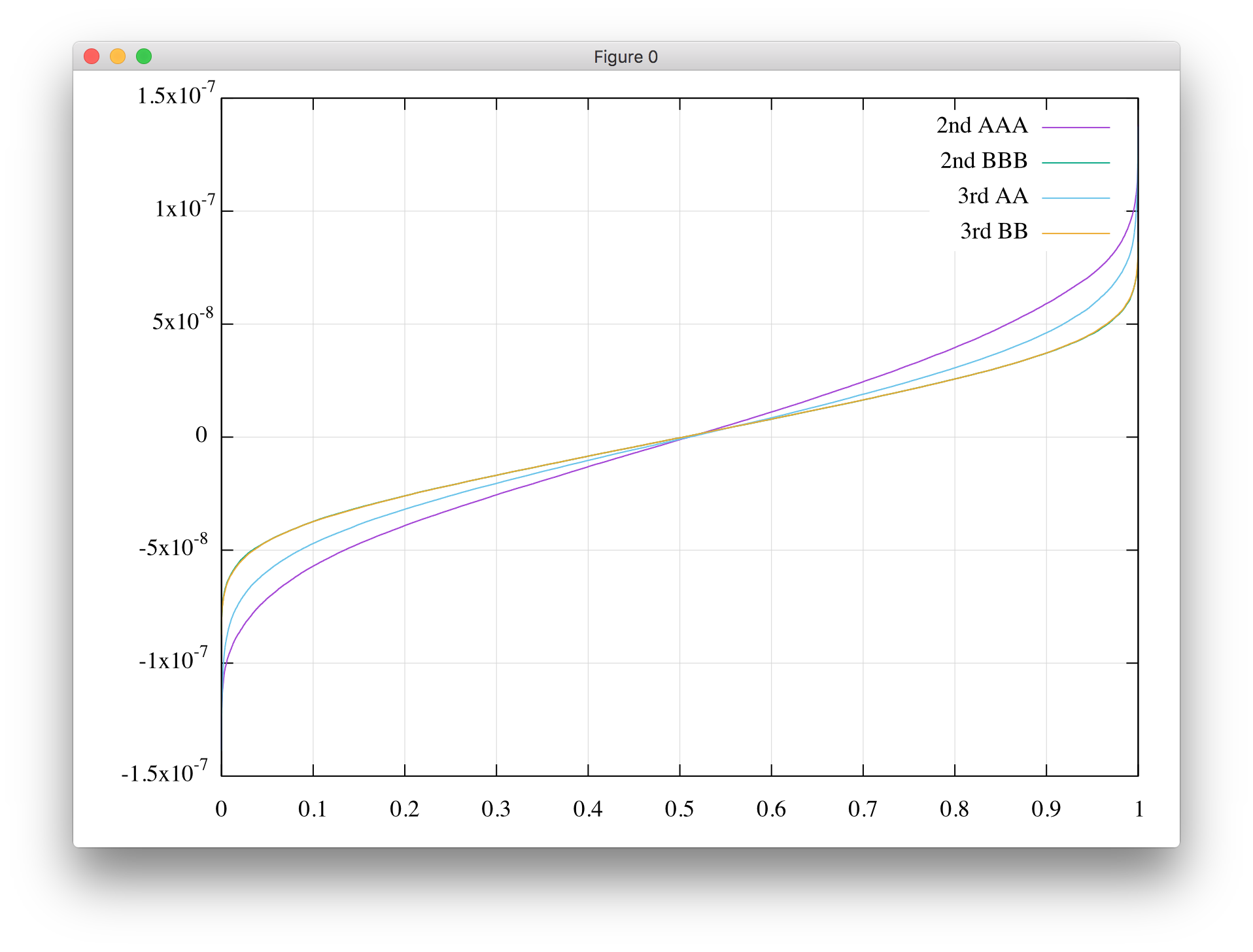
2nd BBB（2倍公式でB方式を3回）と3rd BB（3倍公式でB方式を2回）は殆ど重なってしまっていますが，これは両方ともほぼ同じ値に収束していると考えて良いでしょう（分布ではないく個別の値を見れば一番下のビットは異なります）．単純にBの方式がAの方式よりも丸め誤差が乗りにくいので，少なくとも反復の最後の一回はBの方式を用いるべきでしょう．
また，同じA方式でも，3rd AAの方が2nd AAAより若干良いといという結果となっています．理由については推測の域を出ないのですが，2倍の収束公式では入力の誤差$\epsilon$が正でも負でも改善後の誤差$\epsilon^2$が正になってしまい，一方奇数倍の公式では符号は保存するというのが効いているのかもしれません．
中央付近を拡大してみたものが以下になります．

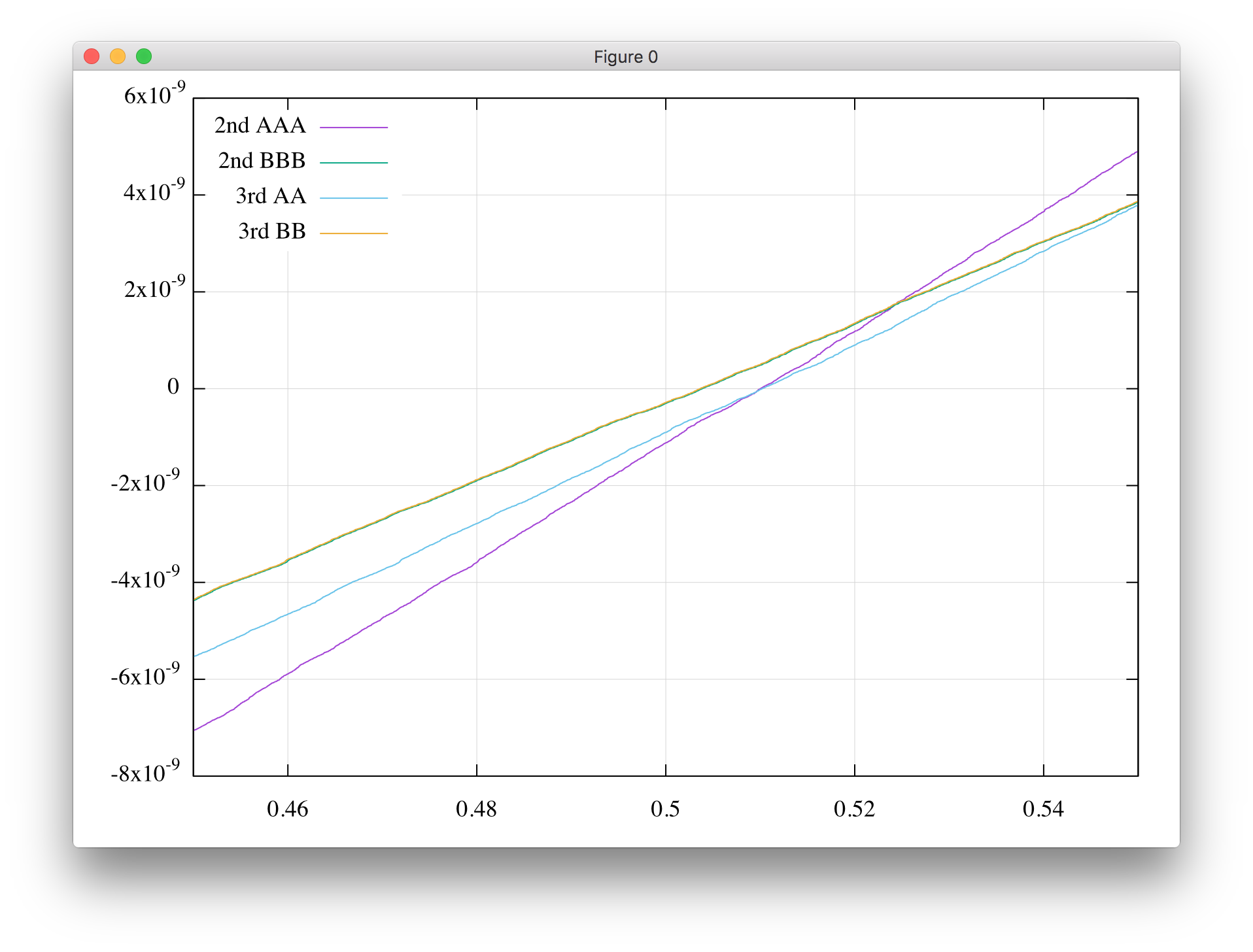
曲線が(0.5, 0)のところで点対称になっているのが誤差に対してバイアスが乗っていない（何度も計算を繰り返したときに結果に誤差が積もりにくい）ということで望ましいのですが，交差点は少しずれています．こちらを比べても，B方式がA方式よりも優れています．

#更に誤差を減らす方法

上のB方式でも，実は誤差はfloat(1.0/sqrt(double(x))と倍精度で計算してから単精度に丸めたものと比べて大きくなってしまっています．24-bitで表された$y_0$（しかもそれなりによく近似できている）に同じく24-bitの補正値（$\Delta y_0$としましょう）が下の方の桁まで正しく計算できていれば，倍精度で計算してから単精度に丸めたものと遜色のない精度が期待できそうなものです．実際，精度のボトルネックとなっている計算は，
$$
h = 1 - x y_0^2
$$
の箇所になります．この計算では，$y_0 \sim 1/\sqrt{x}$という近似にどのぐらいの誤差が入っていたかを評価しています．$x y_0^2$が$1$に近ければ近いほど，それだけ良い近似であったことになります．しかし，1から1に近い値を引くという操作では大きな桁落ちが発生してしまいます（例えば$1-0.997=0.003$では3桁が1桁になってしまいます）．このため，どんなに収束公式を反復しても結果は「正しい値の最近接遇数」に収束してくれるとは限りません（振動するもしくはずれた値に収束する）．どうにかして$h$の有効な桁数を稼ぐ必要があります．

逆数近似の場合には，（先ほどちょこっと出てきた）FMA (fused multiply-add)が有効です．逆数近似では$y_0 \sim 1/x$としてから
$$
h = 1 - x y_0
$$
を評価します．同じじゃないかと思われる方もいるかとは思いますが，FMAの演算機では，$x y_0$の乗算結果の48-bitを24-bitまで丸めること無く，1.0fから引いてくれます．十進数で例えるなら，
$$
1 - 1.01 \times 0.99 = 1 - 0.9999 = 0.00001
$$
という計算，これが途中で$0.9999 \simeq 1.00$と丸められてしまえば桁が残りませんが，FMAなら正しく計算できるんです．

しかし，，，
$x y_0^2$を72-bitとまではいわなくとも48-bitで欲しいなどといってもそのような三重積を高精度に扱ってくれるハードウェアというのは聞いたことがありません（あったら面白いとは思うけど）．一度$x y_0$か$y_0^2$を評価した時点で積が24-bitまで丸められてしまいます．なのでここではFMAを使い丸められてしまった値を復活させるという，主に倍々精度計算ライブラリ³で用いられている技法を試してみます．

\begin{aligned}
y^2 :=& y \times y \\
\Delta y^2 :=& y \times y - y^2 
\end{aligned}

こうやると$y^2 \oplus \Delta y^2$の2語で，48-bitの$y^2$を表現できます（$:=$で左辺に代入されるときにのみ丸められるものと見てください）．今回も十進数で例えるのがわかりやすいでしょう：
$$
0.99 \times 0.99 = 0.9801 = 0.98 + 0.0001
$$
最初の乗算で積が$0.98$まで丸めてしまっても，FMAで最右辺のかたちまで復元できるのです．
$y^2$が誤差なく表現できたので，精度良く$h$を求めて収束させるコードも書いてみます．

static inline float conv_2nd_C(float x, float y){
    float y2 = y * y;
    float yc = __builtin_fmaf(y, y, -y2);
    float  h = __builtin_fmaf(-0.5f*x, y2, 0.5f);
    float hc = __builtin_fmaf(-0.5f*x, yc, h);

    float ret =  __builtin_fmaf(y, hc, y);

    return ret;
}

static inline float conv_3rd_C(float x, float y){
    float y2 = y * y;
    float yc = __builtin_fmaf(y, y, -y2);
    float  h = __builtin_fmaf(-x, y2, 1.0f);
    float hc = __builtin_fmaf(-x, yc, h);

    float ret =  __builtin_fmaf(y, hc*(0.5f + 0.375 * hc), y);

    return ret;
}

こんな感じで$h = (1-xy^2) - x \Delta y^2$を計算しています．追加で2つのFMA命令を必要としますが，収束の最終段にだけこれを使うのがよいでしょう（C方式としておきます）．

誤差はこんな感じになりました（サンプル数を16Mに増やしてあります）．

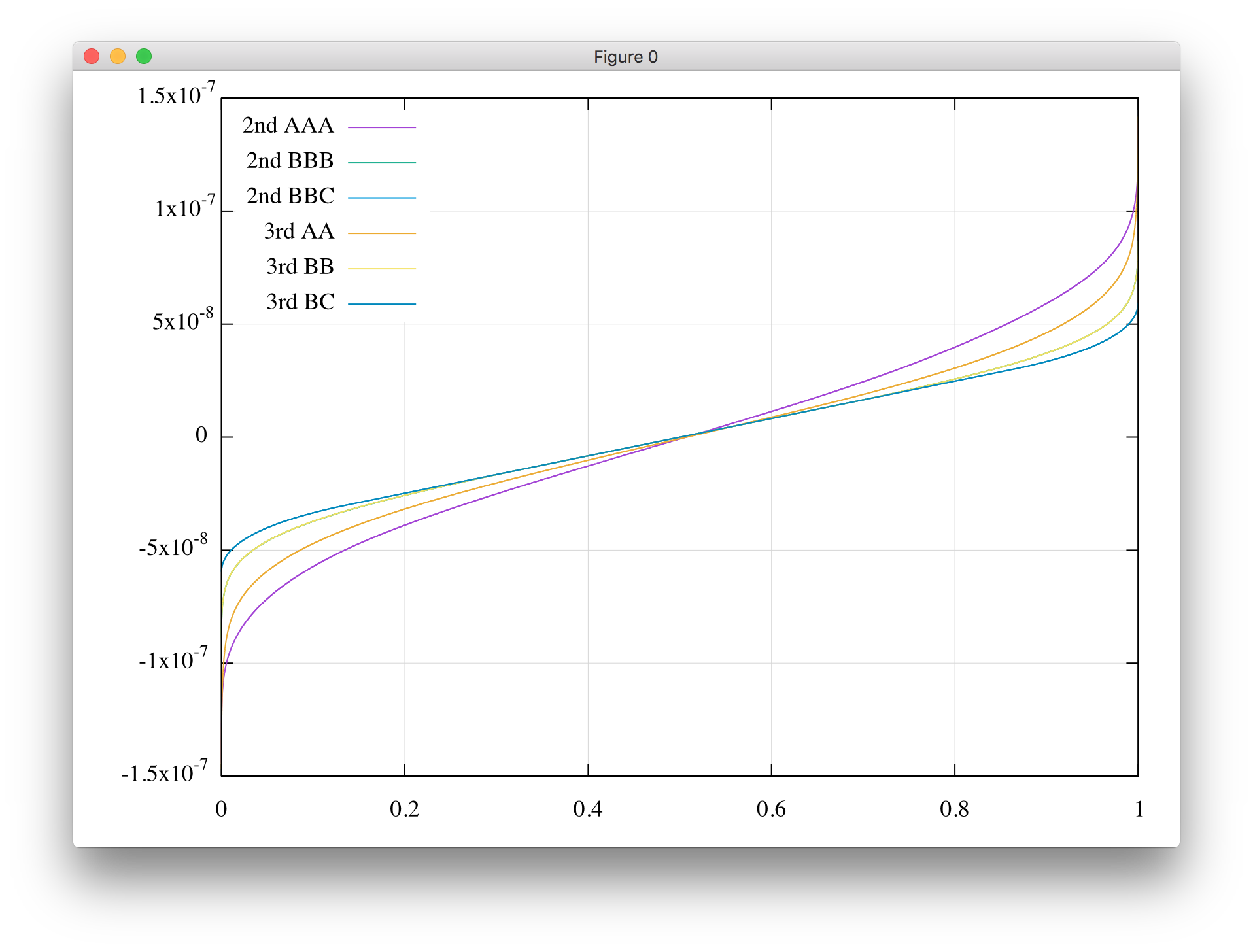
相変わらず2ndと3rdが重なっていてすみません（BBBの上にBBが，BBCの上にBCが重なっています）．確かに精度が改善されています．倍精度で計算してから単精度に丸めたものと比較しても，極稀に最下位ビットが異なってしまうこと（どちらに丸めてもほぼ0.5 ULPとなるような境界ケースです）があるのですが，こうやって分布を目視するレベルでは区別できない程度にまでなりました．
中心部の拡大です．

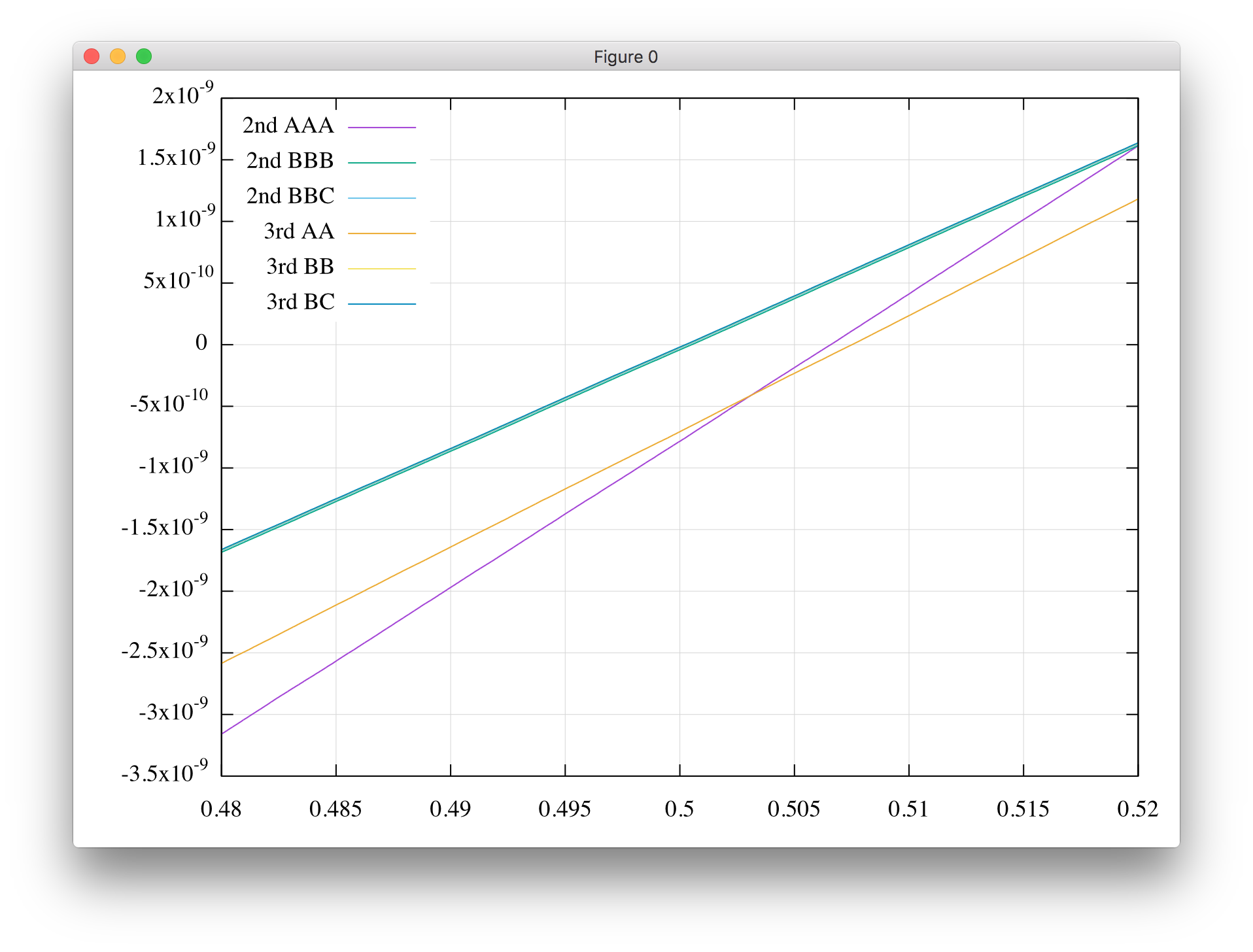
A方式で終わらなければ，バイアスは乗らないようです（上の方のガタガタした図は統計精度が悪かった）．

おわりに

「最後の1-bitにまでこだわって何が楽しいんだ（何の役に立つんだ）」というのはごもっともな指摘で，数値ライブラリの設計を仕事にしているとかでない限りは殆ど趣味の世界です．しかしこうやって突き詰めてみると，言語によってはREALなんて型名で提供されている浮動小数点型の演算というのは，筆算をした後毎回決まった桁で四捨五入をしているようなものだとうことがよく実感できます．また，例外的にFMAは，$d = \pm a \times b \pm c$の計算に対して一度しか丸めが入らないこと，桁落ちの気になる箇所にFMAがキマると爽快ですね，といったところでしょうか．
あと，単精度で切り捨て丸めのモードしかサポートされていないハードウェア（昔あったんですよ本当に）でまともな精度の数値計算をしようとかいった場合（窓から投げ捨てるのが正解），この手の知識やテクニックは重宝するかもしれません．

1. 今回のテストでは*と+で書かれた式をコンパイラ（g++）が勝手にFMAにしていました．環境によっては異なる結果が得られるのでご了承くださいm(_ _)m． ↩

2. 今clang++でコンパイルしたらg++とはFMAの方針が違ったようで結果が変わってしまいました．FMAの有無による精度差は今後調べることにします． ↩

3. QDというライブラリの取説の日本語訳がhttps://na-inet.jp/na/qd_ja.pdfにあります． ↩