楕円軌道
前回は特異点(シンギュラリティ)のある1次元問題という特殊ケースでしたが今回は同様の手法(Mikkola & Tannikawa, 1999; Preto & Tremaine, 1999)でもう少し普通な2次元ケプラー問題をやってみみようと思います。
時間変換後の運動方程式は、
\begin{aligned}
&\frac d{ds}\begin{pmatrix}t \\ x \\ y\end{pmatrix} =
\frac{1}{p_t + \frac12( {v_x}^2 + {v_y}^2) }
\begin{pmatrix} 1 \\ v_x \\ v_y \end{pmatrix}
\\
&\frac d{ds}\begin{pmatrix} p_t \\ v_x \\ v_y\end{pmatrix} =
\frac{-1}{x^2 + y^2}
\begin{pmatrix} 0 \\ x \\ y \end{pmatrix}
\end{aligned}
のようになります。
コードはこんな感じ:
struct Kepler2D{
// Fictitious time
double s;
// Coordinates
double t, rx, ry;
// Momentum
double pt, vx, vy;
Kepler2D(const double e){
s = 0.0;
t = 0.0;
rx = 1.0 + e;
ry = 0.0;
pt = 0.5;
vx = 0.0;
vy = sqrt((1.0 - e)/(1.0 + e));
}
void drift(const double h){
double v2 = vx*vx + vy*vy;
double dtds = h / (pt + 0.5*v2);
t += dtds;
rx += dtds * vx;
ry += dtds * vy;
}
void kick(const double h){
double h_ri2 = h / (rx*rx + ry*ry);
vx -= h_ri2 * rx;
vy -= h_ri2 * ry;
}
void leapfrog_dkd(double h){
drift(0.5 * h);
kick(h);
drift(0.5 * h);
s += h;
}
void dump(FILE *fp = stdout){
double r = sqrt(rx*rx + ry*ry);
double v2 = vx*vx + vy*vy;
double gamma = r * (0.5*v2 - 1/r + pt);
fprintf(fp, "%e %e %e %e %e %e %e\n", s, t, rx, ry, vx, vy, gamma);
}
};
離心率$e$を入力したら遠点から始まるようにしています。
$e=0.99$で回してみました。
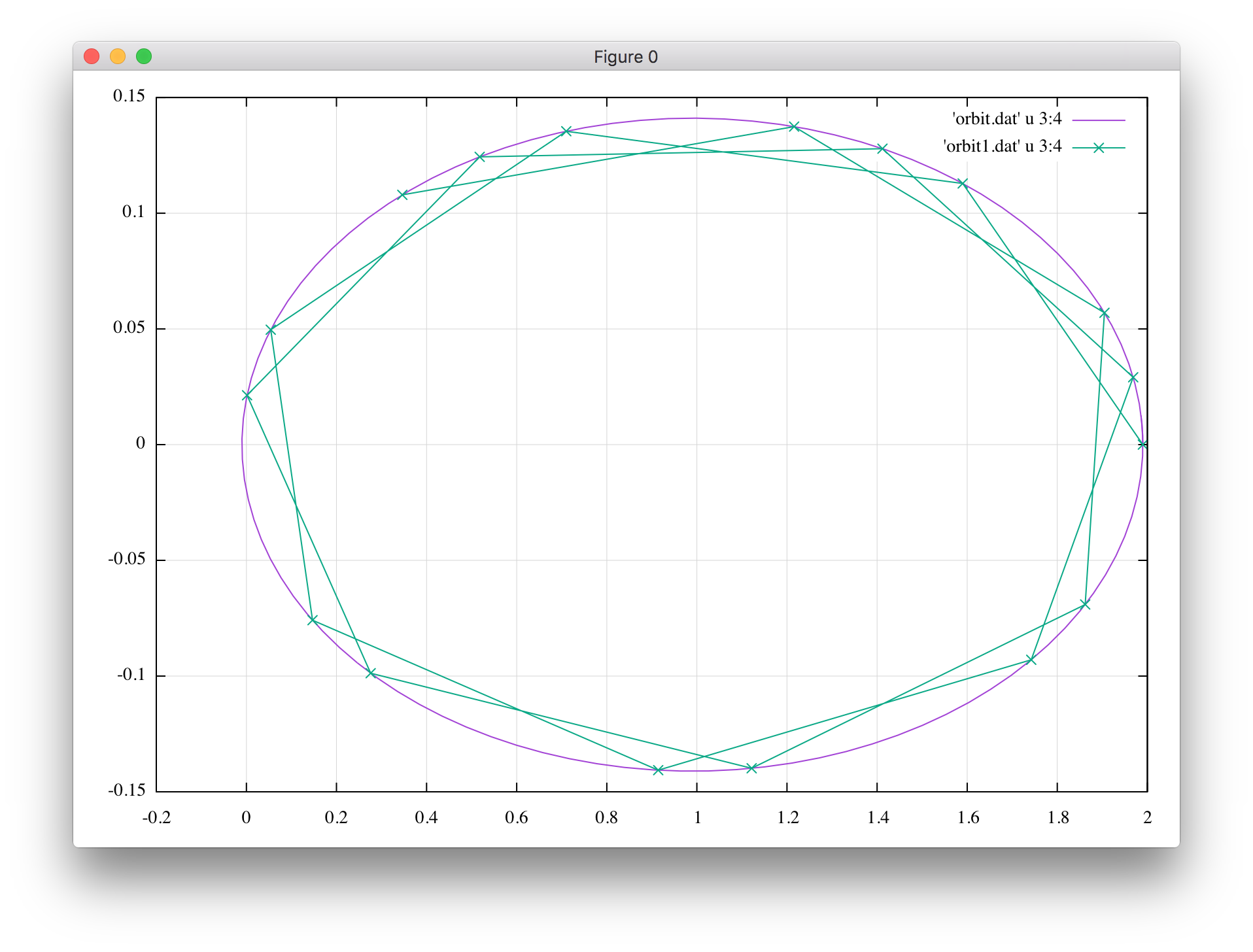
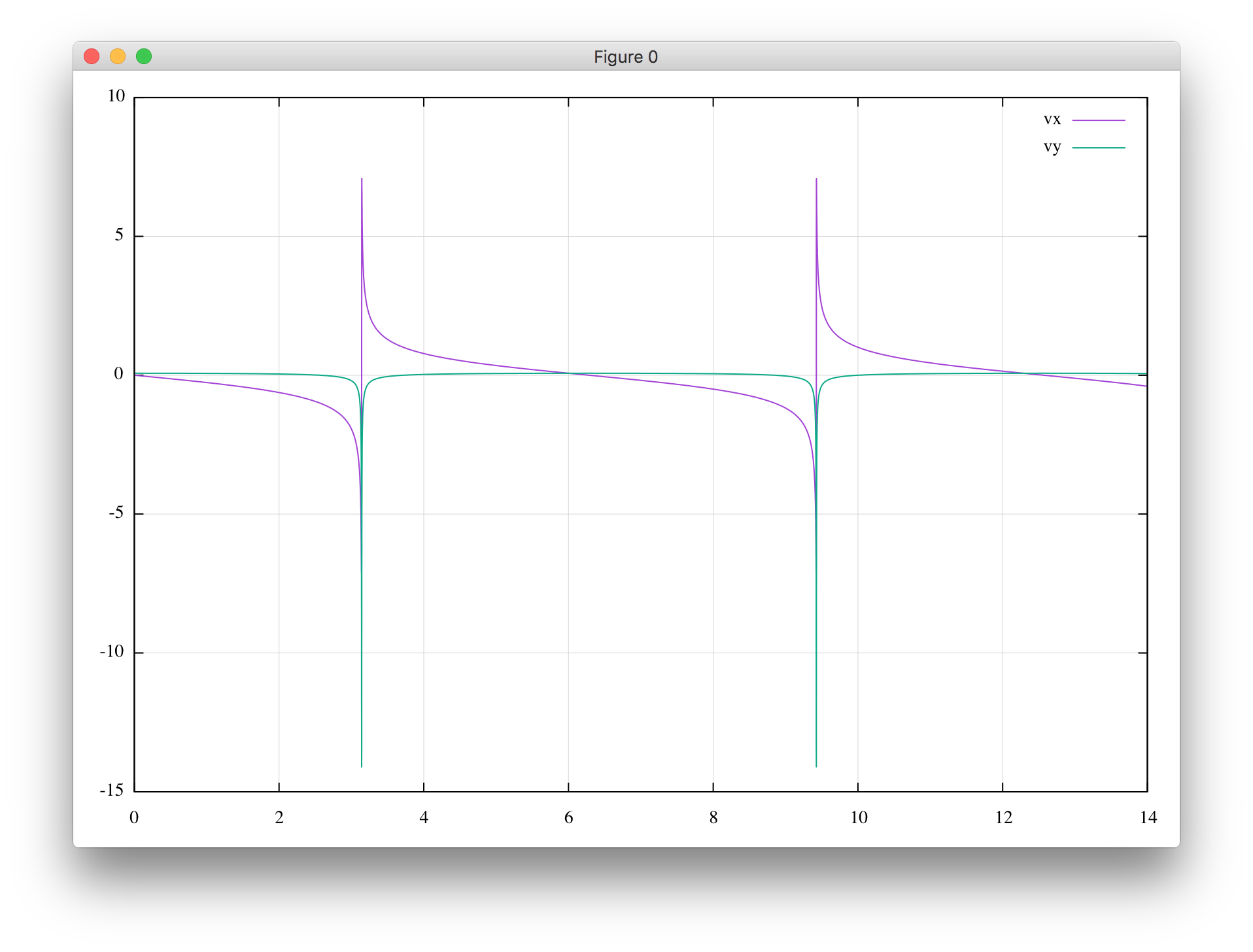
ちゃんと楕円軌道になっています。緑の線は時間刻みを非常に大きく($h=1$)にしてみたものです。近点をスルーしながらも楕円から外れることはありません。
仮想時間$s$に対するハミルトニアン$\Gamma$ですが、非常によく保存します。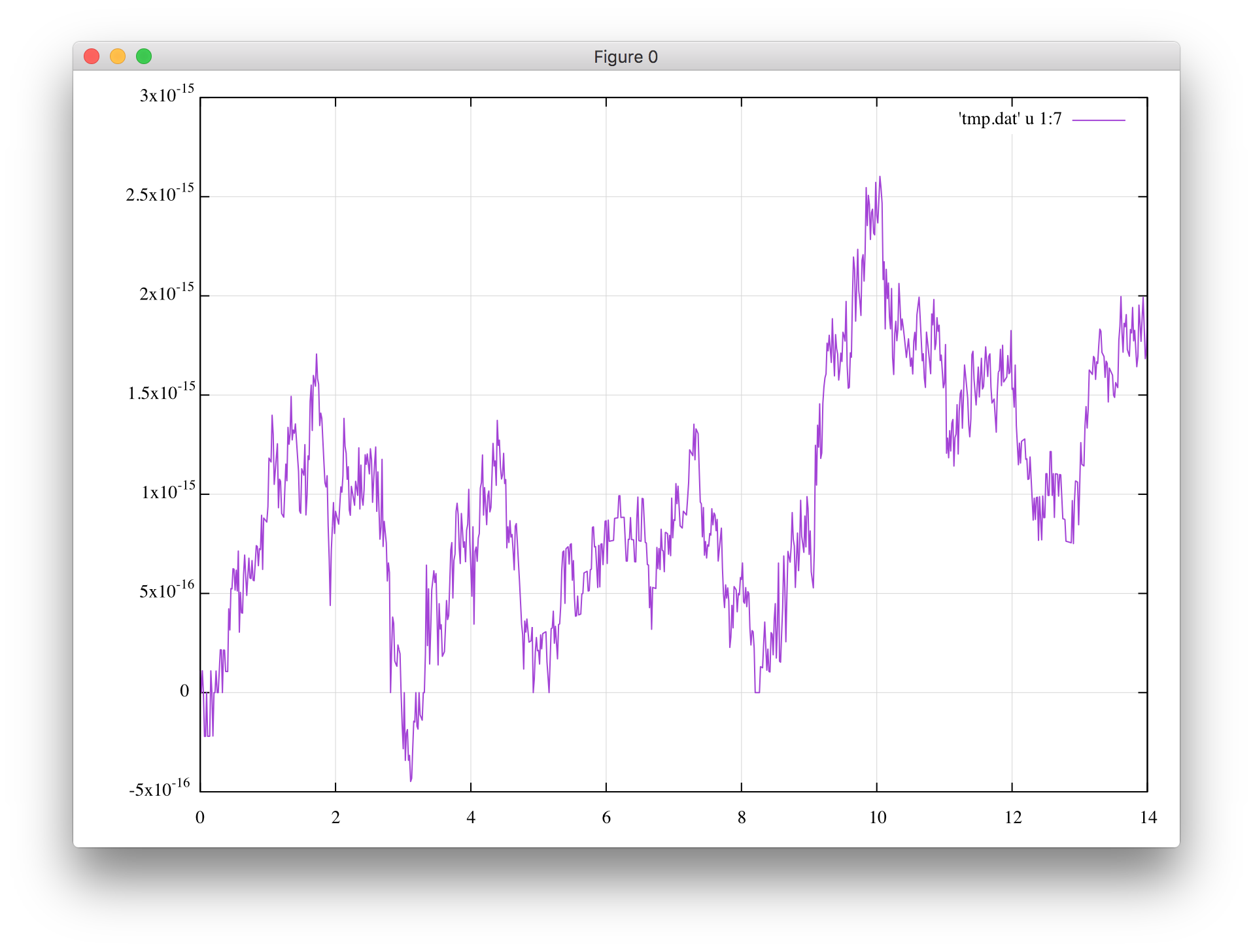
ランダムな丸め誤差のようにも見えますが、近点通過の時刻$t=s=(2n+1)\pi$のときに一桁大きく飛ぶ傾向があるようです。
円軌道
なんだかエネルギーの保存が良すぎるので一番簡単な円軌道($e=0$)の場合に何が起きているのか追いかけてみることにします。実時間でのケプラー問題や調和振動子に対して、symplecticなleapfrog法は誤差が一定以上大きくならないとくことはあっても、誤差そのものが乗らないということはないからです。
初期条件は
\begin{cases}
x = 1 \\
y = 0
\end{cases}
,\quad
\begin{cases}
v_x = 0 \\
v_y = 1
\end{cases}
とします。
刻み幅$h/2$でdriftした後、
\begin{cases}
x = 1 \\
y = h/2
\end{cases}
座標が本来の円軌道の外側にきています。
刻み幅$h$でkickした後、
\begin{cases}
v_x = \dfrac{-h}{1+h^2/4} \\
v_y = \dfrac{1-h^2/4}{1+h^2/4}
\end{cases}
今度は${v_x}^2 + {v_y}^2 = 1$が満たされていることに注意してください。
再び$h/2$でdriftした後、
\begin{cases}
x = \dfrac{1-h^2/4}{1+h^2/4} \\
y = \dfrac{h}{1+h^2/4}
\end{cases}
同様に$x^2 + y^2 = 1$の円軌道上に戻りました。
表にまとめておきます。
| $s$ | $0$ | $h/2$ | $h$ |
|---|---|---|---|
| $x$ | $1$ | $1$ | $\dfrac{1-h^2/4}{1+h^2/4}$ |
| $y$ | $0$ | $h/2$ | $\dfrac{h}{1+h^2/4}$ |
| $v_x$ | $0$ | ー | $\dfrac{1-h^2/4}{1+h^2/4}$ |
| $v_y$ | $1$ | ー | $\dfrac{-h}{1+h^2/4}$ |
ここで出てきた式は(解析解の)$\cos h$と$\sin h$の近似となっています。
\begin{align}
\cos h \sim& \frac{1-h^2/4}{1+h^2/4} = 1 - \frac12 h^2 + \frac18 h^4 - \frac1{32} h^6 + \cdots \\
\sin h \sim& \frac{h}{1+h^2/4} = h - \frac14 h^3 + \frac1{16} h^5 - \frac1{64} h^7 + \cdots
\end{align}
$h^2$の項まで一致しています。$x^2 + y^2 = 1$や${v_x}^2 + {v_y}^2 = 1$も満たされています。つまり解析解に対して数値解は位相だけずれていて保存量に誤差は乗らないわけです。
位相の誤差については、
\begin{align}
\arctan \left( \frac{h}{1-h^2/4} \right)
=& h - \frac2{3}\left( \frac h 2 \right)^3 + \frac2{5}\left( \frac h 2 \right)^5 - \frac2{7}\left( \frac h 2 \right)^7 + \cdots \\
=& 2 \arctan \left(\frac h 2 \right)
\end{align}
のようになっています(展開してみて$\arctan$の半角公式に気が付きました)。本来の位相よりも$h^2$のオーダーで位相が遅れること、収束する条件は$h<2$であることなどがわかります。数値解の位相が遅れることがわかっているので、本当の刻み幅$h$より少し大きな刻み幅:
\tilde h = 2 \tan \left(\frac h 2 \right)
で積分してやれば、位相の遅れを補正することもできます。実際
\begin{align}
\cos h =& \frac{1-\tilde h^2/4}{1+\tilde h^2/4} \\
\sin h =& \frac{\tilde h}{1+\tilde h^2/4}
\end{align}
を確認することができます。
PS:こんな記事もありました。
Wikipedia: Tangent half-angle substitution
もう一度、調和振動子
一番単純な調和振動子
H = \frac12 \left(q^2 + p^2 \right)
に対して位相遅れのみが発生して$H$の値そのものは完全に保存するという性質は実は陰的な2次の積分法、台形公式と中点公式にも共通しています([https://arxiv.org/abs/1708.07266] の3.3.1)。というか、位相への誤差の乗り方も数値解のかたちも前節の数式と全く同じです。ただし意外だったのは、陽的なDKD公式でも時間変換をした円軌道の問題で全く同じ結果が得られたことです。まぁ、導関数に除算が入っているという違いもあります。
ただ、座標に$x, y$、速度に$v_x, v_y$と合計4変数ある系でこのような結果が得られたとはいえ釈然としないので、$q, p$の2変数で同じような結果が得られる方法を考えてみます。振幅を決める全エネルギーは初期条件から、
E = \frac12 \left(q(0)^2 + p(0)^2 \right)
のようにします。これは定数扱いとし、$H$とは違って$q$や$p$で偏微分しても$0$になるものとします。こうやって調和振動子の運動方程式を
\left\{
\begin{aligned}
\dot q =& \dfrac{2E}{q^2 + p^2} p \\
\dot p =& \dfrac{-2E}{q^2 + p^2} q
\end{aligned}
\right.
のように書きます。分母に$q^2 + p^2$が現れたのがポイントで、解析解ではここは$2E$と一致しますが、数値計算のときはこの限りではありません。この微分方程式に対して修正中点法や2段2次のRunge–Kutta法を用いると、中点では$q^2+p^2$が少し大きな値となり、終点では前節のような位相誤差のみを含む値が得られます。保存量で運動方程式を式変形すると数値解の振る舞いが変わるというのは面白いですね。
で、こんな運動方程式を生成するハミルトニアンは存在するのかというと、
H = E \ln \left( q^2 + p^2 \right)
が一応(偏微分すると運動方程式になるという意味で)そうなっています。なんだか不思議なかたちですね。