はじめに
1次元Kepler問題
H = \frac12 v^2 - \frac1r
を考えます。$r$が座標、$v$が速度です（$q$と$p$じゃなければ気持ち悪いという人は適宜置き換えてください）。1次元だから2次元や3次元よりも簡単そうなのですが、厄介なのは単調減少する$r$が必ずや$r=0$の特異点（シンギュラリティ）に突入するということです。
でもご安心ください。厳密解が無くても厳密でない数値計算は進められることがあります。以下、数学や解析力学について雑な記述が続きますことをあらかじめお詫びしておきます。
時間変換と運動方程式
実時間$t$に対して仮想時間$s$を
dt = r ds
のように導入します。時間に対する常微分方程式は、
\frac{d}{ds} = r \frac{d}{dt}
で変換します。
以下微分方程式の時間変換とハミルトニアン力学がごっちゃになっていて、導出と呼べるものにはなっていません。
時間変換した後のハミルトニアンは、
\Gamma(t, r, p_t, v) = \frac{dt}{ds}\bigl( H(r,v) + p_t \bigr)
で、$t$も座標のひとつとなってそれに対応する運動量が$p_t$となっています。導出は省きます（単に私の勉強不足です）が、$p_t$はエネルギーの逆符号となっています。元の$H$は数値的にはエネルギーだったのですが、$\Gamma$の方は値は$0$となります（大事なのは値よりは偏微分の結果ですが）。ちゃんとした導出を追いたい方は、「拡大相空間」"extended phase space"のキーワードで調べてみてください。
とりあえず積分する量のセットを
- 座標：$(t, r)$
- 運動量：$(p_t, v)$
にわけて考えます。$p_t$は今回外部からの摂動を考えないので定数になります。
実時間$t$での微分から仮想時間$s$での微分に変換するには単に$r$を掛けるだけなのですが、座標の導関数に座標が入るとあまり具合が良くないのですが、エネルギーの方程式
-p_t = \frac12 v^2 - \frac1r
を使って
\frac{d}{ds}
= r \frac{d}{dt}
= \frac{1}{p_t + \frac12 v^2} \frac{d}{dt}
とすれば座標と運動量の導関数が互いに依存するかたちに書き下せます：
- 座標
\frac{d}{ds}
\begin{pmatrix} t \\ r \end{pmatrix}
=
\frac{1}{p_t + \frac12 v^2} \frac{d}{dt}
\begin{pmatrix} t \\ r \end{pmatrix}
=
\frac{1}{p_t + \frac12 v^2}
\begin{pmatrix} 1 \\ v \end{pmatrix}
- 運動量
\frac{d}{ds}
\begin{pmatrix} p_t \\ v \end{pmatrix}
=
r \frac{d}{dt}
\begin{pmatrix} p_t \\ v \end{pmatrix}
=
\begin{pmatrix} 0 \\ -\frac1{r} \end{pmatrix}
離散化
座標の（仮想）時間微分は運動量から、運動量の時間微分は座標から計算できるようになりました。このときLeapfrog（蛙跳び）積分法が使えます。座標をアップデートする操作をDriftと呼び（等速直線運動をします）、
D(h) : q \gets q + h \frac{dq}{ds}
また運動量のアップデート操作をKick（こっちは座標が固定）といいます。
K(h) : p \gets p + h \frac{dp}{ds}
$D(h/2)K(h)D(h/2)$ないし$K(h/2)D(h)K(h/2)$の操作を組み合わせることで、それぞれDKD、KDKモードと呼ばれる2次精度Leapfrog積分法を構築できます。今回のハミルトニアンにはDKDがお勧めらしいので、DKDモードを実装してみます。
struct Kepler1D{
double t, r;
double pt, v;
Kepler1D(){
t = 0.0;
r = 2.0;
pt = 0.5;
v = 0.0;
}
void drift(const double h){
double dtds = h / (pt + 0.5*v*v);
t += dtds;
r += dtds * v;
}
void kick(const double h){
v -= h / r;
}
void dump(double s, FILE *fp = stdout){
double gamma = r * (0.5*v*v - 1/r + pt);
fprintf(fp, "%e %e %e %e %e\n", s, t, r, v, gamma);
}
};
初期条件は軌道長半径が$a=1$、離心率が$e=1$となるように取りました。
int main(){
Kepler1D sys;
double h = 1./16.;
sys.dump(0.0);
for(int i=0; i<100000; i++){
sys.drift(0.5 * h);
sys.kick(h);
sys.drift(0.5 * h);
sys.dump(h*(1+i));
}
}
#結果
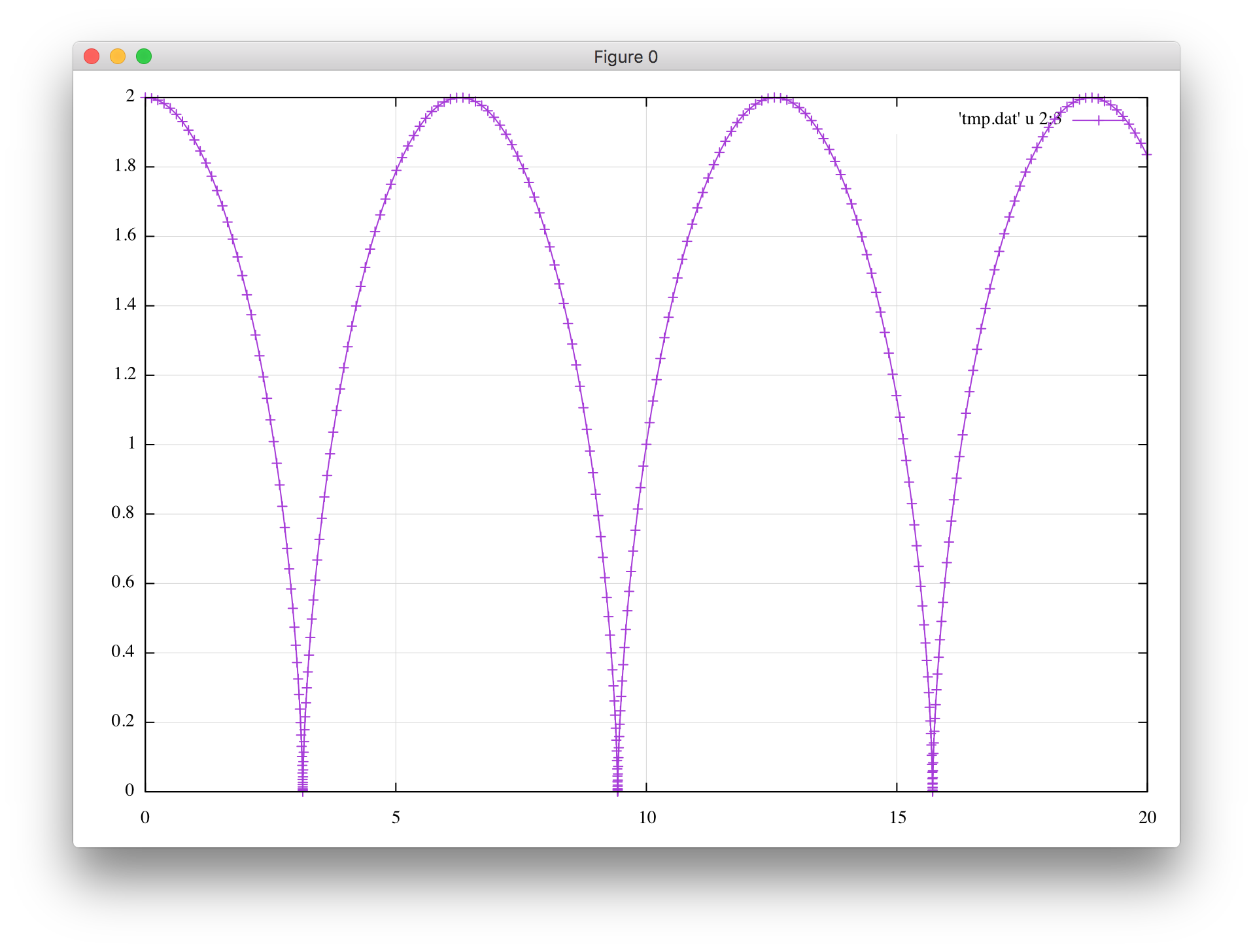まず実時間$t$に対する座標$r$です。綺麗に跳ね返ってますね。これを「解」とみなしていいのかは悩ましいですが、楕円運動から始めて離心率$e \to 1$の極限を取ったものと解釈可能です。今回の数値計算で原点付近で何が起こったかというと、最初のDriftの後座標$r$が小さな負の値になり、次のKickで速度$v$の符号が反転、最後のDriftで$r$の符号が正に戻っていることで跳ね返りが実現しているようです。
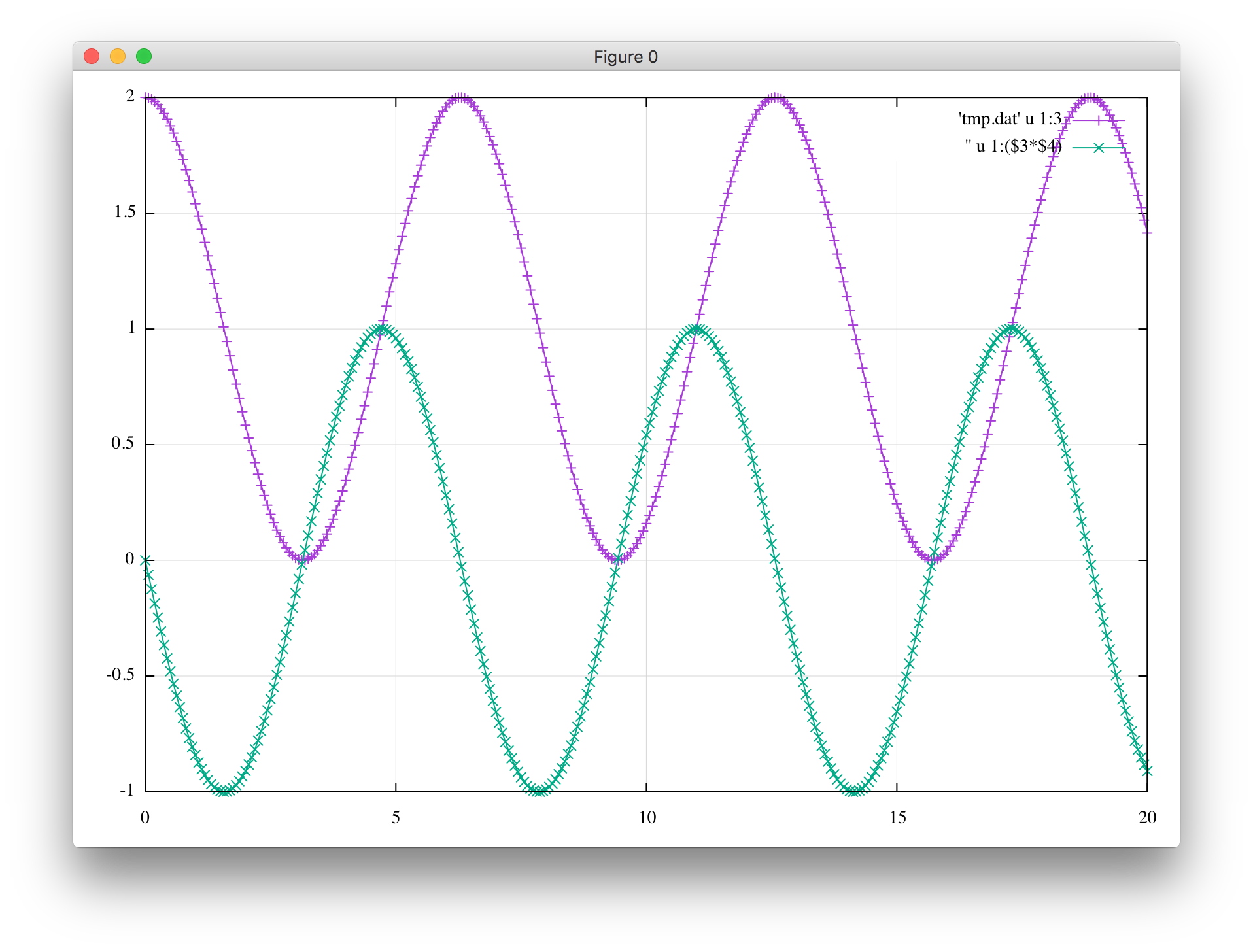仮想時間$s$に対して座標$r(s)$と$dr/ds = rv$をプロットしてみたものです。こちらはきれいな調和振動子になっていて、特異点のことを忘れて安心してみていられますね。
「特異点 踏まなければ 怖くない」（字足らず）
本当にこんな方法で大丈夫なのでしょうか？数値的には特異点のごく近くを何度も通っています。長めにまわして速度$v$を見てみましょう。
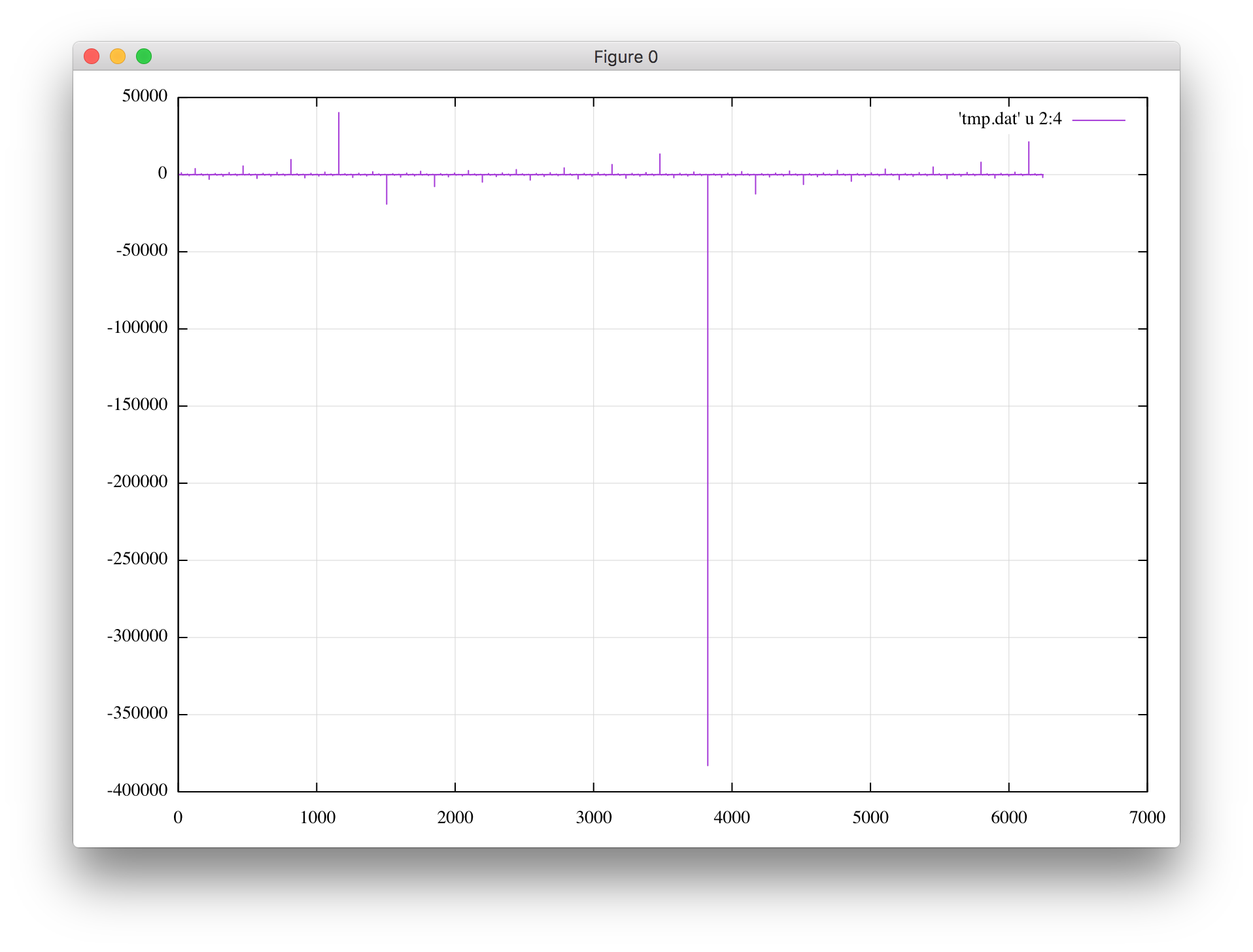
殆ど運任せですがなかなかNaNにはなりません。ハミルトニアン$\Gamma$の値も見てみましょう。
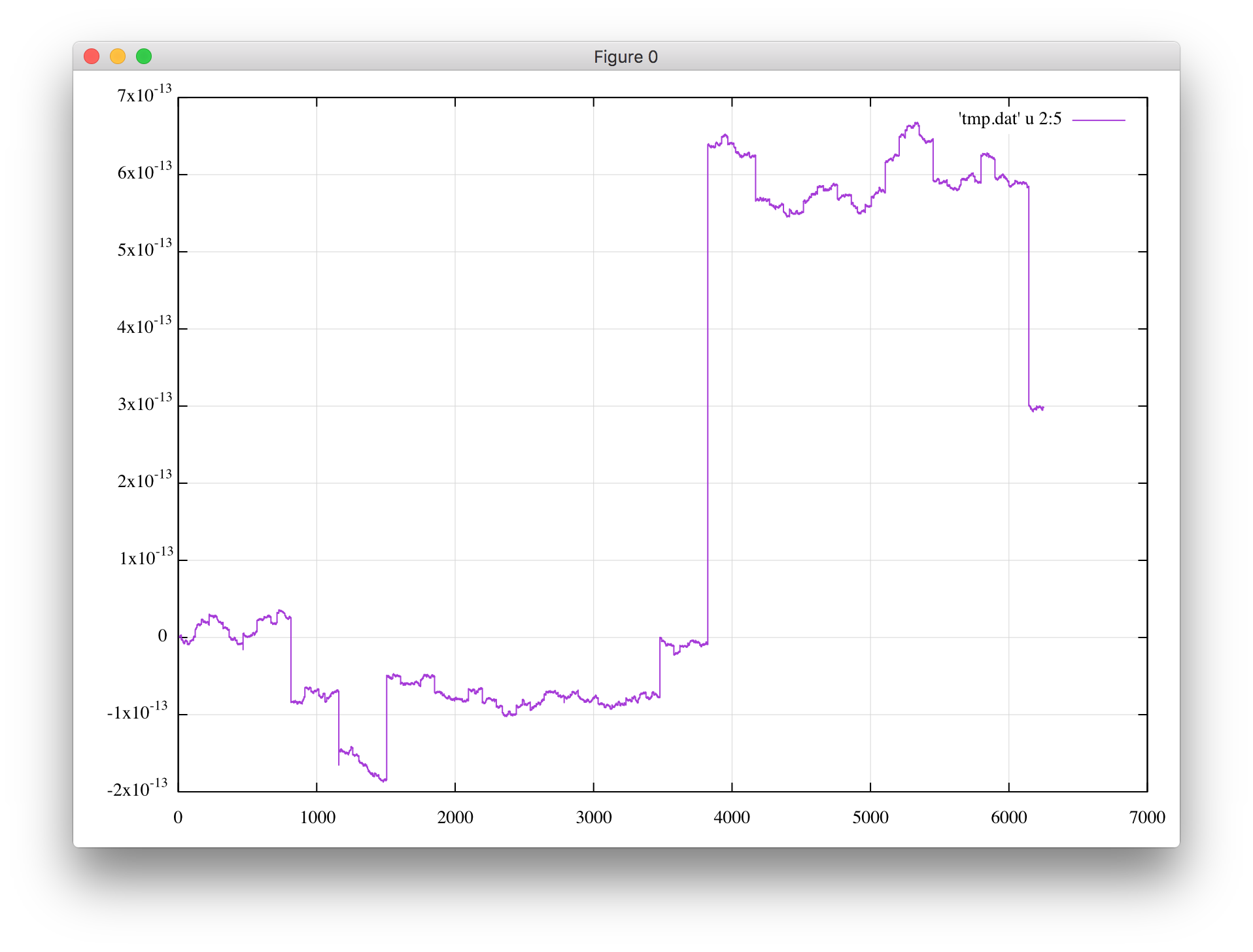
丸め誤差程度でランダムウォークしている（＝理想的な振る舞い）にも見えますが、特異点のすぐ近くを通ったときには比較的大きなジャンプが発生しています。信じられない程うまく動いているのですが、調和振動子になる$rv$ではなく$v$を積分しているため丸め誤差からは逃れられません。
#参考文献
Extended phase spaceでのsymplectic integratorについてもっとちゃんとした記述を見たい方は以下をあたってください。ほぼ同時に同じ手法が独立に発明されたことで伝説となっている２本です。