Ateam Lifestyle x cyma Advent Calendar 2018の20日目は、株式会社エイチームでWebエンジニアをしている@k_moriが担当します。
はじめに

地球上に生息する生命体の多くは、長い時間を経て姿形を変化させながら、種が生存していくのに適した形に進化を重ねてきた歴史があります。
この「進化」という生物学的機構にヒントを得て考案された問題解決手法に**「進化的アルゴリズム」というものがあります。
この「進化的アルゴリズム」は数学的理論から生み出されたような専門的な知識がなければ理解が難しい手法などではないため、比較的理解もしやすく、機械が自分自身で成長する仕組み(≒人工知能)がなぜ実現できるのかを理解するのにもオススメなアルゴリズムかなと思います。
この記事では、そんな「進化的アルゴリズム」の一種である、「遺伝的アルゴリズム」と「遺伝的プログラミング」**を筆者が実際に実装してみて分かった、使い方や優れている点、懸念点などをまとめていきたいと思います。
まとめだけ読みたい方はこちらからどうぞ。
こんな方にオススメ
- 人工知能とか機械学習とかの理屈がよく分からない人
- 機械学習とかちょっと興味あるけど、何から学習し始めたら良いか分からない人
- 「遺伝的アルゴリズム」と「遺伝的プログラミング」の違いがわからない人、使い方がわからない人
- 自分で機械学習の仕組みを実装してみたい人
- とにかく何でもいいから文章を読みたい人
そもそも進化的アルゴリズムとは?
進化的アルゴリズムとは、前述したように「進化」という生物学的機構にヒントを得て考案された手法です。
記事を読み進めていただければ理解いただけることかもしれませんが、地球上の生命体がありとあらゆる形に進化できる可能性を持っている中で、それぞれの種が生き延びていくのにふさわしい形に進化してきた仕組みに着想を得ていることから、「選択肢は何万通りとあるが、どれを選択するべきか分からない」、**「どのように組み合わせるべきか分からない」**といった問題の解決手段に向いています。
アルゴリズムの説明に入る前に

「遺伝的アルゴリズム」と「遺伝的プログラミング」は問題解決手法であり、実際に実装する際には、何かしらの解決したい問題が存在している方が分かりやすいです。
「遺伝的アルゴリズム」と「遺伝的プログラミング」は「どれを選択するべきか分からない」という問題の解決に向いているため、今回はいわゆる**「ナップサック問題」**に挑戦してみたケースで説明していきたいと思います。
(「ナップサック問題」自体がどういった問題なのかは、記事の主題とズレるためWikipediaのページをご参照ください)

また今回は、筆者が「遺伝的アルゴリズム」と「遺伝的プログラミング」に対して、実装を通して深い理解を得る目的もあるため、機械学習や演算処理などのライブラリが豊富なPythonをあえて使わず、JavaScriptで実装を試みています。
JavaScriptを選定したのは、筆者の開発経験と動作環境手配の容易さが理由です。
なお筆者は機械学習に精通しているわけでもJavaScriptに精通しているわけでもありません。もし記事の内容に誤りのある内容などがありました際には、ご指摘いただけますと幸いです。
遺伝的アルゴリズム
まずはじめに遺伝的アルゴリズムから説明していきたいと思います。
ちなみに遺伝的プログラミングよりも先に遺伝的アルゴリズムを説明するのは、遺伝的プログラミングが遺伝的アルゴリズムの応用形のような形になっており、先に遺伝的アルゴリズムを理解しておくことで、理解するのが易しくなるからです。
アルゴリズムの全体像
遺伝的アルゴリズムは、以下のような流れで処理を進めます。

このような処理のループを繰り返すことで、少しずつ評価の高い(求めたい解に近い)データを生成していきます。
この図ではループの終了条件に触れていませんが、「評価が○○以上になったら」でもいいですし、「〇〇回ループしたら」でも良いです。
特にルールはありませんが「評価が○○以上になったら」という実装ですと、永遠に期待以上の評価になれず無限ループとなってしまう恐れが生まれるので、「〇〇回ループしたら」という実装は最低限しておくことを個人的にオススメします。
それでは、各処理ごとに細かく説明していきます。
前準備
今回はナップサック問題を解くことに挑戦しますので、
問題の設定となる「ナップサックの容量」と、ナップサックに積み込む「アイテム一覧」を定数で用意しておきます。
(アイテム一覧の値はランダムに生成したものです)
// ナップサックの最大容量
var KNAPSACK_WEIGHT_CAPACITY = 300;
// アイテム一覧、[重量, 価値]
var ITEMS = [
[6, 71],
[4, 29],
[78, 44],
[63, 73],
[23, 42],
[60, 72],
[14, 60],
[19, 79],
[16, 6],
[9, 72],
[8, 32],
[74, 23],
[42, 23],
[2, 92],
[85, 36]
];
初期集団の生成
ナップサック問題の最終解答となる「どのアイテムを入れるべきかを表すデータ」をランダムに複数個生成します。
init: function () {
this.oneGenerationItemCount = 20; // 1世代での個体数
this.geneItemCount = ITEMS.length; // 候補アイテムの数
...中略...
this.genesAtGeneration = new Array(this.oneGenerationItemCount);
for(var i = 0; i < this.oneGenerationItemCount; i++) {
this.genesAtGeneration[i] = this.createRandomPutsItemGene();
}
...中略...
},
// ナップサックの容量範囲内でナップサックに入れるアイテム一覧をランダムに選択する
createRandomPutsItemGene: function() {
var _this = this;
var puts_item_gene = '';
var random_gene = 0;
var enable_puts_into_knapsack = false;
while(!enable_puts_into_knapsack) {
puts_item_gene = '';
for( var i = 0; i < _this.geneItemCount; i++) {
random_gene = Math.floor(Math.random()*2);
puts_item_gene += String(random_gene);
}
// ナップサックの容量を超えていないかチェック
enable_puts_into_knapsack = _this.calculateKnapsackValue(puts_item_gene) !== false;
}
return puts_item_gene; // ex) '001101111101100'
},
ここでは、1世代で20個のデータを用意する設定にしたので、20個のランダムデータを生成しています。
また、「calculateKnapsackValue」(後述)という関数を用意して、ランダムとはいえナップサックの容量範囲内のデータが作られるようにしています。
適応度の評価
生成されたデータがどれくらい優れているか、各データごとに評価します。
// 探索処理
simulateAtOneGeneration: function () {
var _this = this;
// 1世代分の個体達すべてでナップサックに実際にアイテムを入れるシミュレーションを行う
var genesArray = _this.genesAtGeneration;
var resultsArray = new Array(_this.oneGenerationItemCount);
for(var itemNo = 0; itemNo < _this.oneGenerationItemCount; itemNo++) {
// ナップサックに入れるアイテム価値の総和を求める
resultsArray[itemNo] = _this.calculateKnapsackValue(genesArray[itemNo]);
}
...中略...
},
// 引数のアイテムをナップサックに入れた場合の価値総和を求める、ナップサックの最大容量を超えた場合はfalse
calculateKnapsackValue: function(puts_item_gene) {
var total_weight = 0;
var total_value = 0;
items = puts_item_gene.split("");
for(var i = 0; i < items.length; i++) {
if(Number(items[i])) {
total_weight += ITEMS[i][0];
total_value += ITEMS[i][1];
if(total_weight > KNAPSACK_WEIGHT_CAPACITY) {
return false;
}
}
}
return total_value;
}
選択
評価の高かったデータを元にして進化させていくために、評価の高かったデータが次世代のデータに残りやすい形でデータを選択します。
// 交叉で引数分の子供をつくる
createChildren: function(genesArray, resultsArray) {
var _this = this;
var children = new Array(_this.oneGenerationItemCount);
// ルーレット選択で、次の世代候補を選択
var minimumValue = 0;
for(var i = 0; i < _this.oneGenerationItemCount; i++){
minimumValue = (minimumValue > resultsArray[i]) ? resultsArray[i] : minimumValue;
}
minimumValue = Math.abs(minimumValue);
var total = 0;
for(var i = 0; i < _this.oneGenerationItemCount; i++){
total += (resultsArray[i]+minimumValue);
}
for(var x = 0; x < _this.oneGenerationItemCount; x++){
var arrow = Math.floor(Math.random()*total);
var sum = 0;
for(var i = 0; i < _this.oneGenerationItemCount; i++){
sum += (resultsArray[i]+minimumValue);
if(sum > arrow){
children[x] = genesArray[i];
break;
}
}
}
...中略...
ここでは**「ルーレット選択」**という手法を用いて実装しました。これは以下のようなイメージで、評価の値が高いほど、その評価値の比率に応じて選択されやすくする方法です。
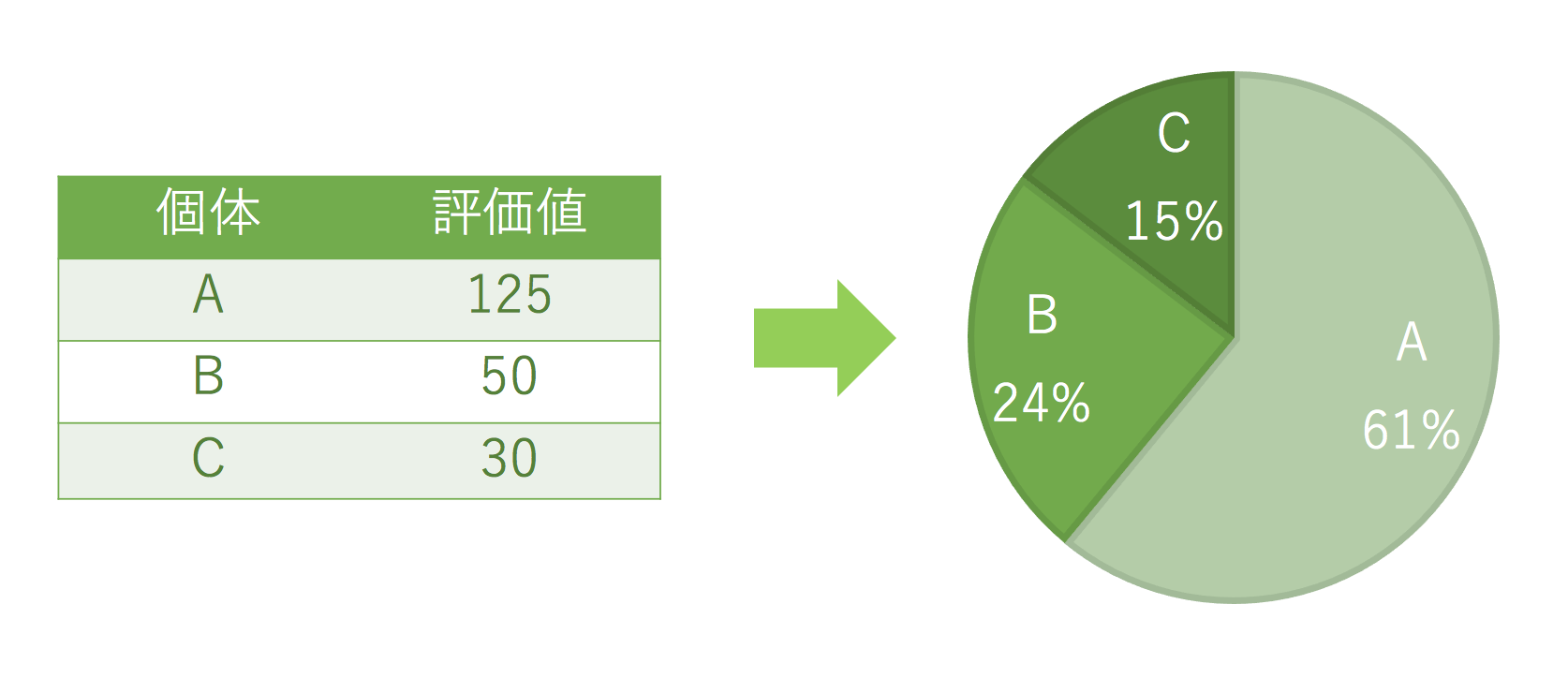
ただし「ルーレット選択」は、「評価値がマイナスにならないこと」が前提だったり、「評価の差が激しいと評価が高いデータだけが極端に生き残りやすくなる」という懸念もあり、この方法が一番優れているわけではないという点に注意です。
他にも「ランキング選択」や「トーナメント選択」など、色々な選択方法が考案されています。このあたりは調べると色々出てくると思いますので、実装する前に一度どんなものがあるのか調べてみることをオススメします。
交叉
交叉では、生き残ったデータ同士を掛け合わせて、親データの特徴を持った新しい子データを生み出します。
// 交叉で引数分の子供をつくる
createChildren: function(genesArray, resultsArray) {
...中略(「選択」部分)...
// 交叉(前から2組ずつ交叉する。交叉しなければそのままコピーされる)
for(var x = 0; (_this.oneGenerationItemCount % 2 === 1 && x < _this.oneGenerationItemCount - 1) ||
(_this.oneGenerationItemCount % 2 === 0 && x < _this.oneGenerationItemCount); x+=2){
// 交叉は一定確率で起こるものとする
if(Math.floor(Math.random()*100) < (100-_this.mutantRate)){
// ランダムに交叉点を決定
var randomCutStartNo = Number(Math.floor(Math.random()*_this.geneItemCount));
var randomCutEndNo = randomCutStartNo;
while(randomCutStartNo === randomCutEndNo) {
randomCutEndNo = Number(Math.floor(Math.random()*_this.geneItemCount));
}
if(randomCutStartNo > randomCutEndNo) {
var tmpNo = randomCutStartNo;
randomCutStartNo = randomCutEndNo;
randomCutEndNo = tmpNo;
}
// 交叉
var childrenEven = children[x].substring(0, randomCutStartNo)
+ children[x+1].substring(randomCutStartNo, randomCutEndNo + 1)
+ children[x].substring(randomCutEndNo + 1, _this.geneItemCount);
var childrenOdd = children[x+1].substring(0, randomCutStartNo)
+ children[x].substring(randomCutStartNo, randomCutEndNo + 1)
+ children[x+1].substring(randomCutEndNo + 1, _this.geneItemCount);
children[x] = childrenEven;
children[x+1] = childrenOdd;
}
}
return children;
},
上記のプログラムでは以下のようなことを行なっています。
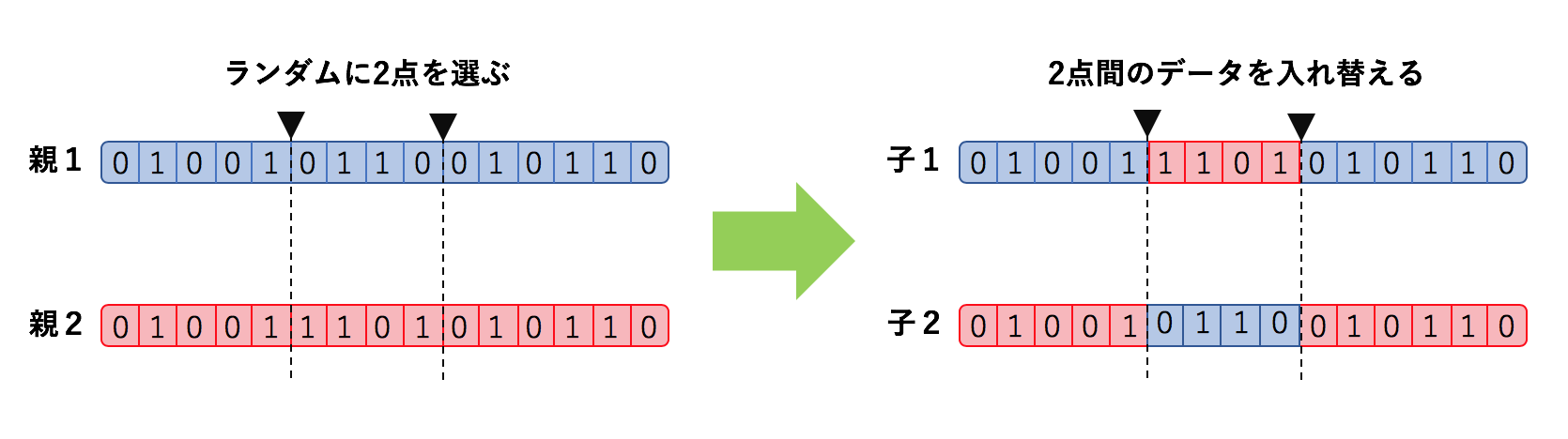
こうすることで、「両親の特徴を持った子供を作る」といったことを実現しています。
まさに遺伝子を受け継ぐ染色体の動きを模しているようです。
上記の場合は**「二点交叉」**という交叉方法なのですが、ここに関しても他に「多点交叉」や「一様交叉」という別の交叉手法が存在します。
突然変異
親に似たデータばかりを生成しているとデータに偏りが生じ、より優れた特徴を持つデータが存在したとしても発生しづらくなります。
そのため、一定の確率でデータに突然変異を起こします。
// 次の世代の個体を用意する
createNewGenerations: function(elitesArray, childrensArray) {
var _this = this;
// 子孫個体に一定確率で突然変異を起こさせる
var newGenerations = new Array(_this.oneGenerationItemCount);
for(var i = 0; i < _this.oneGenerationItemCount; i++) {
newGenerations[i] = childrensArray[i];
}
for(var j = 0; j < _this.oneGenerationItemCount; j++) {
var mutantrate = Number(Math.floor(Math.random()*100));
if(mutantrate < _this.mutantRate) {
var geneNo = Number(Math.floor(Math.random()*_this.geneItemCount));
var mutantGenChar = String((Number(newGenerations[j].charAt(geneNo))+1)%2);
newGenerations[j] = newGenerations[j].substr(0,geneNo) + mutantGenChar + newGenerations[j].substring((geneNo+1),_this.geneItemCount);
}
}
...中略...
},
ここではデータの中のランダムな箇所の値を変更することで、突然変異を起こしています。
ex) 00010111'0'101100 => 00010111'1'101100
実際のプログラム実行結果
プログラム中に進化の様子をロギングする処理を入れておくことで次のような結果を得ることができました。
current generaion:1 current max value gene:111001010110010 current max value:491
current generaion:2 current max value gene:111001010110010 current max value:491
current generaion:3 current max value gene:111001010110010 current max value:491
current generaion:4 current max value gene:111001010110010 current max value:491
current generaion:5 current max value gene:111001010110010 current max value:491
current generaion:6 current max value gene:111001010110010 current max value:491
current generaion:7 current max value gene:111010110110010 current max value:521
current generaion:8 current max value gene:111100110110010 current max value:552
current generaion:9 current max value gene:111100110110010 current max value:552
current generaion:10 current max value gene:111100110110010 current max value:552
current generaion:11 current max value gene:111110110110010 current max value:594
current generaion:12 current max value gene:111110110110010 current max value:594
current generaion:13 current max value gene:111110110110010 current max value:594
current generaion:14 current max value gene:111011110111010 current max value:616
current generaion:15 current max value gene:111111110110010 current max value:666
current generaion:16 current max value gene:111111110110010 current max value:666
current generaion:17 current max value gene:111111110110010 current max value:666
current generaion:18 current max value gene:111111110110010 current max value:666
current generaion:19 current max value gene:111111110110010 current max value:666
current generaion:20 current max value gene:111111110110010 current max value:666
current generaion:21 current max value gene:111111110110010 current max value:666
current generaion:22 current max value gene:111111110110010 current max value:666
current generaion:23 current max value gene:111111110110010 current max value:666
current generaion:24 current max value gene:111111110110010 current max value:666
current generaion:25 current max value gene:111111110110010 current max value:666
current generaion:26 current max value gene:111111110110010 current max value:666
current generaion:27 current max value gene:111111110110010 current max value:666
current generaion:28 current max value gene:111111110110010 current max value:666
current generaion:29 current max value gene:111111110110010 current max value:666
current generaion:30 current max value gene:111111110110010 current max value:666
世代が進むにつれ、より評価の高いデータが生成されているのが分かります。
また、第15世代目以降からは評価が頭打ちになり、それ以上進化できていないことも分かります。
今回用意したデータでは「666」という値にまでできることが分かりました。
実際のプログラムコード全文はコチラに置いてあります。
遺伝的プログラミング
遺伝的プログラミングは遺伝的アルゴリズムと基本的な考え方は同じで、
「初期集団の生成」→「適応度の評価」→「選択」→「交叉」→「突然変異」→「適応度の評価」→...という流れで処理していきます。
ですので遺伝的アルゴリズムが理解できていれば遺伝的プログラミングを理解するのも難しくはないと思いますが、進化させていくデータ構造に違いがありますので、その点に絞って重点的に説明していきたいと思います。
遺伝的プログラミングの特徴
遺伝的プログラミングでは、進化させていくデータの構造に木構造を用います。
これにより、求めたい解が単純な1次元配列などでは表せない複雑な内容、主に関数そのものなどを求めたい時に有用な手段となります。
実際に関数を木構造で表すのに、以下のような形を用います。
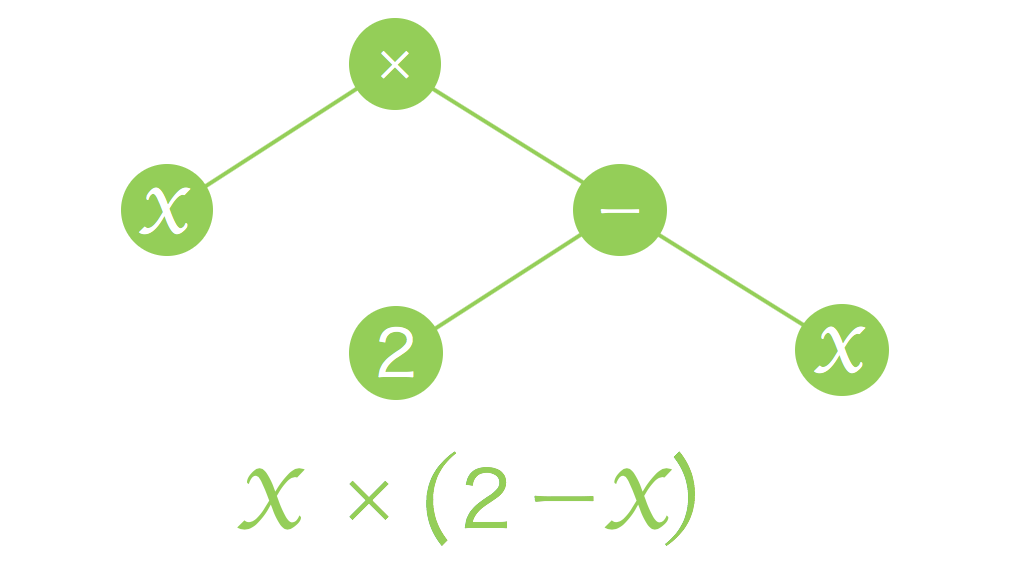
上記の場合は、$x×(2-x)$という関数を表していることになります。
ナップサック問題を解くにあたり、実際の実装方法として今回は以下のようなデータ構造の型を用意して実現しました。
// 遺伝的プログラミングで遺伝子の表現に用いる木構造のノード
var geneTreeNode = function(operator, item_no, num) {
this.operator = operator; // 演算子
this.item_no = item_no; // 左辺ノード : アイテムNo(ITEMS定数のインデックス) or 木構造
this.num = num; // 右辺ノード : アイテムの積載数量 or 木構造
...中略...
};
遺伝的プログラミングでは遺伝的アルゴリズムよりも複雑な解を求めることが可能になったために、ナップサックに同じアイテムを複数個積み込むことができるという仕様にしれっと変更しています。
(遺伝的アルゴリズムではアイテムごとに「入れるか」「入れないか」の2択でした)
これは遺伝的アルゴリズムで用いるデータ構造では表現が難しいため求めることが出来ませんでしたが、遺伝的プログラミングだからこそ求められる高度な解と言えるでしょう。
交叉
交叉は以下のように木構造のランダムに選択されたノード同士を入れ替える方式で行います。
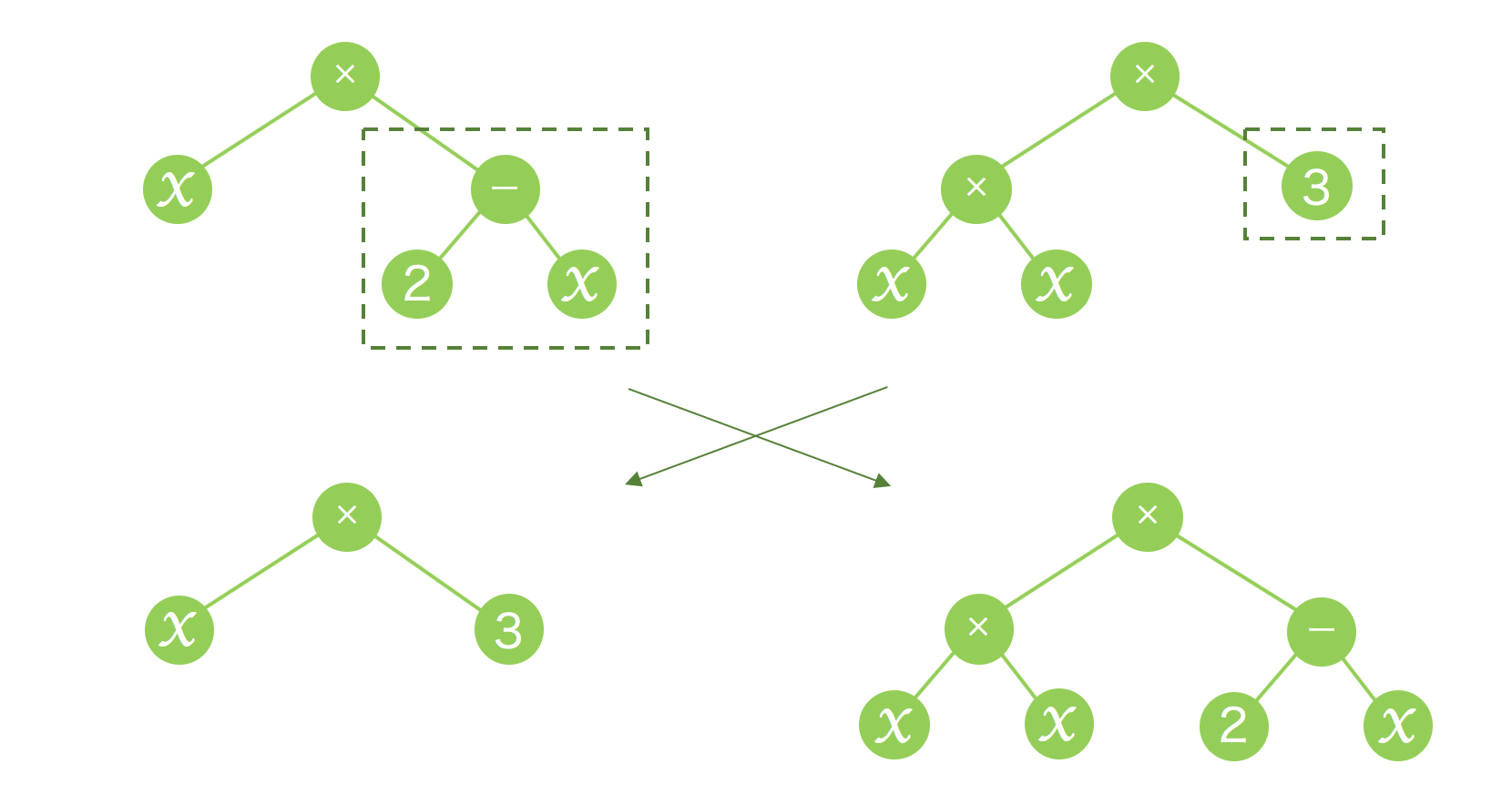
プログラムでは以下のようにして実現しました。
// 交叉(前から2組ずつ交叉する。交叉しなければそのままコピーされる)
for(var x = 0; (_this.oneGenerationItemCount % 2 === 1 && x < _this.oneGenerationItemCount - 1) ||
(_this.oneGenerationItemCount % 2 === 0 && x < _this.oneGenerationItemCount); x+=2){
// 交叉は一定確率で起こるものとする
if(Math.floor(Math.random()*100) < (100-_this.mutantRate)){
// ランダムに交叉点(ノード)を決定
node_ids = children[x].getNodeIdList();
choice_node_id_index = Math.floor(Math.random()*node_ids.length);
even_node_id = node_ids[choice_node_id_index];
even_node = children[x].getNodeById(even_node_id).copyObject();
node_ids = children[x+1].getNodeIdList();
choice_node_id_index = Math.floor(Math.random()*node_ids.length);
odd_node_id = node_ids[choice_node_id_index];
odd_node = children[x+1].getNodeById(odd_node_id).copyObject();
// 交叉
children[x].setNodeById(even_node_id, odd_node);
children[x+1].setNodeById(odd_node_id, even_node);
}
}
突然変異
突然変異は、ノードをランダムに生成したノードに置き換えたり、削除したりして実現します。
// 次の世代の個体を用意する
createNewGenerations: function(elitesArray, childrensArray) {
var _this = this;
// 子孫個体に一定確率(5%)で突然変異を起こさせる
var newGenerations = new Array(_this.oneGenerationItemCount);
for(var i = 0; i < _this.oneGenerationItemCount; i++) {
newGenerations[i] = childrensArray[i];
}
for(var i = 0; i < _this.oneGenerationItemCount; i++) {
var mutantrate = Number(Math.floor(Math.random()*100));
if(mutantrate < _this.mutantRate) {
node_ids = newGenerations[i].getNodeIdList();
choice_node_id_index = Math.floor(Math.random()*node_ids.length);
change_node_id = node_ids[choice_node_id_index];
new_operator = _this.operatorList[Math.floor(Math.random()*2)];
node_depth = newGenerations[i].getDepthById(change_node_id, 1);
mutant_node = _this.createRandomPutsItemGeneTreeNode(new_operator, node_depth);
newGenerations[i].setNodeById(change_node_id, mutant_node);
}
}
...中略...
},
実際のプログラム実行結果
current generaion:1 current max value gene: ([9]*10) current max value:720
current generaion:2 current max value gene: ( ([9]*7) + ([0]*7) ) current max value:1001
current generaion:3 current max value gene: ( ( ([13]*6) + ([10]*4) ) + ([0]*7) ) current max value:1177
current generaion:4 current max value gene: ( ( ([9]*7) + ([0]*7) ) + ([0]*7) ) current max value:1498
current generaion:5 current max value gene: ( ([9]*10) + ( ([6]*10) + ([0]*7) ) ) current max value:1817
current generaion:6 current max value gene: ( ([6]*10) + ( ([6]*10) + ([0]*7) ) ) current max value:1817
current generaion:7 current max value gene: ( ( ([13]*6) + ( ([9]*10) + ([13]*6) ) ) + ([0]*7) ) current max value:2321
current generaion:8 current max value gene: ( ([0]*7) + ([0]*7) ) current max value:2321
current generaion:9 current max value gene: ( ([0]*7) + ([0]*7) ) current max value:2321
current generaion:10 current max value gene: ( ( ([9]*10) + ([9]*10) ) + ( ([0]*7) + ([13]*6) ) ) current max value:2489
current generaion:11 current max value gene: ( ( ([9]*10) + ( ([0]*7) + ([13]*6) ) ) + ( ([0]*7) + ([13]*6) ) ) current max value:2818
current generaion:12 current max value gene: ( ( ( ([9]*10) + ( ([0]*7) + ([13]*6) ) ) + ( ([0]*7) + ([13]*6) ) ) + ([0]*7) ) current max value:3315
current generaion:13 current max value gene: ( ( ( ([9]*10) + ( ([0]*7) + ([13]*6) ) ) + ( ([0]*7) + ([13]*6) ) ) + ([0]*7) ) current max value:3315
current generaion:14 current max value gene: ( ( ( ([9]*10) + ( ([0]*7) + ([13]*6) ) ) + ([13]*6) ) + ( ([9]*10) + ([9]*10) ) ) current max value:3315
current generaion:15 current max value gene: ( ( ( ([9]*10) + ( ([0]*7) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([9]*10) ) ) + ([0]*7) ) current max value:4090
current generaion:16 current max value gene: ( ( ( ([9]*10) + ( ( ( ([9]*10) + ([13]*6) ) + ( ([0]*7) + ([13]*6) ) ) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([9]*10) ) ) + ([0]*7) ) current max value:4090
current generaion:17 current max value gene: ( ( ( ([9]*10) + ( ( ( ([9]*10) + ([13]*6) ) + ( ([0]*7) + ([13]*6) ) ) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([9]*10) ) ) + ([0]*7) ) current max value:4090
current generaion:18 current max value gene: ( ( ( ([9]*10) + ( ( ( ([9]*10) + ([13]*6) ) + ( ([0]*7) + ([13]*6) ) ) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([9]*10) ) ) + ([0]*7) ) current max value:4090
current generaion:19 current max value gene: ( ( ( ( ([13]*6) + ([0]*7) ) + ( ( ([0]*7) + ([0]*7) ) + ([13]*6) ) ) + ( ([9]*10) + ([13]*6) ) ) + ([0]*7) ) current max value:4364
current generaion:20 current max value gene: ( ( ( ( ([0]*7) + ([13]*6) ) + ( ( ([0]*7) + ([0]*7) ) + ([13]*6) ) ) + ( ([13]*6) + ([13]*6) ) ) + ([0]*7) ) current max value:4364
current generaion:21 current max value gene: ( ([13]*6) + ( ( ( ([13]*6) + ([0]*7) ) + ( ( ([0]*7) + ([0]*7) ) + ([13]*6) ) ) + ( ([9]*10) + ([13]*6) ) ) ) current max value:4419
current generaion:22 current max value gene: ( ( ( ([13]*6) + ( ([13]*6) + ([0]*7) ) ) + ( ([13]*6) + ( ( ([13]*6) + ( ([13]*6) + ([0]*7) ) ) + ( ([13]*6) + ([13]*6) ) ) ) ) + ([0]*7) ) current max value:5355
current generaion:23 current max value gene: ( ([13]*6) + ( ( ( ([13]*6) + ([0]*7) ) + ( ( ( ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) + ( ([13]*6) + ([13]*6) ) ) + ([0]*7) ) + ([13]*6) ) ) + ( ([9]*10) + ([13]*6) ) ) ) current max value:6162
current generaion:24 current max value gene: ( ([13]*6) + ( ( ( ([13]*6) + ( ( ([9]*10) + ([13]*6) ) + ( ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) + ( ([13]*6) + ( ( ([13]*6) + ( ([13]*6) + ([0]*7) ) ) + ( ([13]*6) + ( ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) + ( ([13]*6) + ([13]*6) ) ) ) ) ) ) ) ) + ( ( ( ( ([13]*6) + ([13]*6) ) + ( ( ([13]*6) + ([10]*1) ) + ([13]*6) ) ) + ([0]*7) ) + ([13]*6) ) ) + ( ([9]*10) + ([13]*6) ) ) ) current max value:6162
current generaion:25 current max value gene: ( ([13]*6) + ( ( ( ([13]*6) + ( ( ([9]*10) + ([13]*6) ) + ( ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) + ( ([13]*6) + ( ( ([13]*6) + ( ([13]*6) + ([0]*7) ) ) + ( ([13]*6) + ( ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) + ( ([13]*6) + ([13]*6) ) ) ) ) ) ) ) ) + ( ( ( ( ([13]*6) + ([13]*6) ) + ( ( ([13]*6) + ([10]*1) ) + ([13]*6) ) ) + ([0]*7) ) + ([13]*6) ) ) + ( ([9]*10) + ([13]*6) ) ) ) current max value:6162
current generaion:26 current max value gene: ( ( ( ( ([0]*7) + ([13]*6) ) + ( ([13]*6) + ( ( ([13]*6) + ( ( ([13]*6) + ([13]*6) ) + ( ( ([13]*6) + ([10]*1) ) + ([13]*6) ) ) ) + ( ([13]*6) + ([13]*6) ) ) ) ) + ([0]*7) ) + ([0]*7) ) current max value:6491
current generaion:27 current max value gene: ( ( ( ( ([0]*7) + ([13]*6) ) + ( ([13]*6) + ( ( ([13]*6) + ( ( ([0]*7) + ( ( ([0]*7) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) + ( ([13]*6) + ([13]*6) ) ) ) + ( ([13]*6) + ([13]*6) ) ) ) + ( ([13]*6) + ([13]*6) ) ) ) ) + ([0]*7) ) + ([0]*7) ) current max value:6491
current generaion:28 current max value gene: ( ( ( ([0]*7) + ([13]*6) ) + ( ([13]*6) + ( ( ([13]*6) + ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([10]*1) ) + ([13]*6) ) ) ) + ( ([13]*6) + ([13]*6) ) ) ) ) + ([0]*7) ) current max value:6546
current generaion:29 current max value gene: ( ( ( ([0]*7) + ([13]*6) ) + ( ([13]*6) + ( ( ([13]*6) + ( ( ([0]*7) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([10]*1) ) + ([13]*6) ) ) ) + ( ([13]*6) + ([13]*6) ) ) ) ) + ([0]*7) ) current max value:6546
current generaion:30 current max value gene: ( ( ( ([0]*7) + ([13]*6) ) + ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ([13]*6) ) ) ) + ([0]*7) ) current max value:6546
current generaion:31 current max value gene: ( ( ( ( ( ([0]*7) + ([13]*6) ) + ([13]*6) ) + ( ( ( ( ( ([13]*6) + ([10]*1) ) + ( ([13]*6) + ( ( ([0]*7) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) ) ) + ([13]*6) ) + ([13]*6) ) + ([13]*6) ) ) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([0]*7) ) current max value:8179
current generaion:32 current max value gene: ( ( ( ( ( ([0]*7) + ([13]*6) ) + ([13]*6) ) + ( ( ( ( ( ([13]*6) + ([10]*1) ) + ( ([13]*6) + ( ( ([0]*7) + ([13]*6) ) + ([13]*6) ) ) ) + ([13]*6) ) + ([13]*6) ) + ([13]*6) ) ) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([0]*7) ) current max value:8179
current generaion:33 current max value gene: ( ( ( ( ( ([0]*7) + ([13]*6) ) + ([13]*6) ) + ( ( ( ([0]*7) + ([13]*6) ) + ([13]*6) ) + ([13]*6) ) ) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([0]*7) ) current max value:8179
current generaion:34 current max value gene: ( ( ( ( ([13]*6) + ([13]*6) ) + ( ( ( ( ( ([13]*6) + ( ( ([0]*7) + ([13]*6) ) + ([13]*6) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) ) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([0]*7) ) current max value:9306
current generaion:35 current max value gene: ( ( ( ( ([13]*6) + ([13]*6) ) + ( ( ( ([13]*6) + ( ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ( ([13]*6) + ([10]*1) ) ) ) + ([0]*7) ) current max value:9306
current generaion:36 current max value gene: ( ( ( ( ( ( ( ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ([13]*10) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) + ( ( ([13]*6) + ( ( ([0]*7) + ([13]*6) ) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) ) + ([13]*6) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ([13]*6) + ([10]*1) ) ) current max value:11417
current generaion:37 current max value gene: ( ( ( ( ( ( ( ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ([13]*10) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) + ( ( ([0]*7) + ([13]*6) ) + ( ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) + ( ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([13]*6) ) ) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ([13]*6) + ([10]*1) ) ) current max value:11417
current generaion:38 current max value gene: ( ( ( ( ( ( ( ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ([13]*10) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) + ( ( ([0]*7) + ([13]*6) ) + ( ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) + ( ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([13]*6) ) ) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ([13]*6) + ([10]*1) ) ) current max value:11417
current generaion:39 current max value gene: ( ( ( ( ( ( ( ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ([13]*10) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) + ( ( ([0]*7) + ([13]*6) ) + ( ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) + ( ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([13]*6) ) ) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ([13]*6) + ([10]*1) ) ) current max value:11417
current generaion:40 current max value gene: ( ( ( ( ( ( ( ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ([13]*10) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) + ( ( ([0]*7) + ([13]*6) ) + ( ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) + ( ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([13]*6) ) ) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ([13]*6) + ([10]*1) ) ) current max value:11417
current generaion:41 current max value gene: ( ( ( ( ( ( ( ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ([13]*10) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) + ( ( ([0]*7) + ([13]*6) ) + ( ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) + ( ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([13]*6) ) ) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ([13]*6) + ([10]*1) ) ) current max value:11417
current generaion:42 current max value gene: ( ( ( ( ( ( ( ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ([13]*10) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) + ( ( ([0]*7) + ([13]*6) ) + ( ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) + ( ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([13]*6) ) ) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ([13]*6) + ([10]*1) ) ) current max value:11417
current generaion:43 current max value gene: ( ( ( ( ( ( ( ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ([13]*10) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) + ( ( ([0]*7) + ([13]*6) ) + ( ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) + ( ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([13]*6) ) ) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ([13]*6) + ([10]*1) ) ) current max value:11417
current generaion:44 current max value gene: ( ( ( ( ( ( ( ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ([13]*10) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) + ( ( ([0]*7) + ([13]*6) ) + ( ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) + ( ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([13]*6) ) ) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ([13]*6) + ([10]*1) ) ) current max value:11417
current generaion:45 current max value gene: ( ( ( ( ( ( ( ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ([13]*10) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) + ( ( ([0]*7) + ([13]*6) ) + ( ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) + ( ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) ) + ([13]*6) ) ) ) ) + ( ([13]*6) + ([13]*6) ) ) + ( ([13]*6) + ([10]*1) ) ) current max value:11417
current generaion:46 current max value gene: ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ( ( ( ( ([10]*1) + ([13]*6) ) + ([13]*6) ) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) ) ) ) ) ) ) ) + ( ( ( ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) + ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) ) ) current max value:12240
current generaion:47 current max value gene: ( ( ( ([13]*6) + ([13]*6) ) + ( ([13]*6) + ([10]*1) ) ) + ( ( ( ( ([10]*1) + ([13]*6) ) + ([13]*6) ) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) ) ) ) ) ) ) ) + ( ( ( ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) + ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) ) ) current max value:12272
current generaion:48 current max value gene: ( ( ( ([13]*6) + ([13]*6) ) + ( ([13]*6) + ([10]*1) ) ) + ( ( ( ( ([10]*1) + ([13]*6) ) + ([13]*6) ) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ( ( ([13]*6) + ([10]*1) ) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) ) ) ) ) ) ) ) + ( ( ( ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) + ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) ) + ([13]*6) ) + ([13]*6) ) ) ) current max value:12272
current generaion:49 current max value gene: ( ( ( ([13]*6) + ([13]*6) ) + ( ([13]*6) + ([10]*1) ) ) + ( ( ( ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) + ([13]*6) ) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ( ( ([10]*1) + ([10]*1) ) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) ) ) ) ) ) ) ) + ( ( ([13]*6) + ( ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) + ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) ) ) + ([13]*6) ) ) ) current max value:12272
current generaion:50 current max value gene: ( ( ( ([13]*6) + ([13]*6) ) + ( ([13]*6) + ([10]*1) ) ) + ( ( ( ( ( ([13]*6) + ([13]*6) ) + ([13]*6) ) + ([13]*6) ) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ( ( ([10]*1) + ( ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) + ( ( ([13]*6) + ([10]*1) ) + ([13]*6) ) ) ) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) ) ) ) ) ) ) ) ) + ( ( ([13]*6) + ( ( ([13]*6) + ( ([13]*6) + ([10]*1) ) ) + ( ( ([13]*6) + ( ([13]*6) + ([13]*6) ) ) + ([13]*6) ) ) ) + ([13]*6) ) ) ) current max value:12272
遺伝的アルゴリズムと同じく、世代が進むにつれ、より評価の高いデータが生成されているのが分かります。
しかし遺伝的アルゴリズムに比べ、進化が頭打ちになりづらく、50世代目まで進化させてみましたが、終盤近くまで進化を続けているのが確認できます。
また、ナップサックに同じアイテムを複数個積み込むことができるという条件にした結果、遺伝的アルゴリズムと比べ、ナップサック積載アイテムの総評価値を大きく伸ばし、「12272」という値にまでできることが分かりました。
ちなみに今回は比較がしやすいように「遺伝的アルゴリズム」と「遺伝的プログラミング」の両方でナップサック問題を解くことに挑戦しましたが、「遺伝的プログラミング」の実装では実装を容易にするため、ナップサック問題を解くことに限定させることで様々な制限を設けながら実装しました。
(実際のプログラムコード全文はコチラに置いてあります。)
しかし実際は遺伝的プログラミングはもっと複雑なことに応用することが可能なアプローチで、演算子も多くの候補を設けて良いですし、本来は人間が思い浮かべられないような複雑な解を求めるために考案された手法だと思いますので、あまり制限は設けずに自由な発想を求めたい問題に用いた方が、より効果を発揮できると思います。
まとめ
今回、「遺伝的アルゴリズム」と「遺伝的プログラミング」という2つの問題解決手法をより理解するためにも、JavaScriptで無理やり実装してみました。
その結果、以下のようなことが分かりましたのでまとめておきます。
| 遺伝的アルゴリズム | 遺伝的プログラミング | |
|---|---|---|
| 優れている点 | 進化が早い。 比較的単純な分、最適解に近づきやすい。 |
より高度な解を求められる。 |
| 懸念点 | あまり複雑なことはできない。 | 求める解が複雑なため局所解に陥りやすい。 設定値の影響を受けやすい。 |
| 推奨 適用分野 |
例) ・どの選択肢を用いるべきか求める問題 (ナップサック問題、ゲームでよくあるオススメパーティーの選出など) ・近似解の生成 (手書き文字再現など) |
例) ・インプットとアウトプットの関係性を方程式(モデル)にしたい問題 (特徴量の生成、ユーザー指標とCVの関係性推測など) ・モデリングによる推測 (手書き文字の筆記者識別、株価予測など) |
また筆者が実際に実装作業を進める中で、「遺伝的アルゴリズム」と「遺伝的プログラミング」に共通して、進化を左右する値をどのような設定にするのかが非常に大切であるということが分かりました。
これはおそらく「機械学習」と総称されるプログラミングの世界においては全般的に言える話だと思いますが、今回実装した2つの問題解決手法においても、「母集団の個体数を幾つにするのか」「突然変異率は幾つにするのか」「選択や交叉の手法はどのような手法で実装するのか」などなど、様々な要素で進化の進み方が異なってきます。
また、記事の中では紹介しきれませんでしたが、「遺伝的アルゴリズム」や「遺伝的プログラミング」で起きる問題を解決するためのアイデアとして、「エリート選抜」などの様々な技法も存在しています。
実際に今回紹介した手法を用いて何かの問題解決を試みる際には、いろいろな手法を試しながら問題に合った実装方法を模索されることをオススメします。
おわりに

いかがだったでしょうか?
今回の記事を通して伝えたかった内容は**「まとめ」**に全てまとめたつもりですので、正直それ以外の箇所は必要な部分だけ確認いただければ構いません。
はじめに触れた内容ですが、今回紹介した「遺伝的アルゴリズム」と「遺伝的プログラミング」という問題解決手法は、機械学習の分野の中でも比較的理解しやすい内容だったと思います。
難解な数式を理解する必要などもないため、機械が自分自身で少しづつ成長していく理屈を理解するのには良い題材だと思います。
筆者自身はまだまだ人工知能・機械学習の初心者ですが、少しでもこの世界に興味を持ってくれる人が増えていただけたのであれば幸いです。
お知らせ
この記事はAteam Lifestyle x cyma Advent Calendar 2018の20日目の記事でしたが、21日目は株式会社エイチームライフスタイルの@dabitsさんが記事を書いてくれるそうです。こちらもチェックしてみてくださいね。
また、エイチームグループでは、一緒に働けるチャレンジ精神旺盛な仲間を募集しています。興味を持たれた方はぜひエイチームグループ採用サイトを御覧ください。
https://www.a-tm.co.jp/recruit/