どうも!おはえりすめんてんEITAです。
みなさんはYouTuberのはなおさんをご存知ですか?
引用元:はなお - YouTube
阪大卒のエリートで、その知識を活かし、おっぱいを関数で求めたり、急に踊り出すドッキリで話題になりました。
彼が設立した積分サークルは全国に多数の支部を抱えており、全国でたくさんの会員が活動しているようです。
ちなみに冒頭の「おはえりすめんてん」は彼が動画の最初で行なっている挨拶になります。
大学対抗おっぱい関数選手権に衝撃を受ける
そんな彼が衝撃的なイベントを開催します...その名も大学対抗おっぱい関数選手権大会(パワーワード)。
私はあまり数学を学んでこなかったので終始ちんぷんかんぷんでしたが、今までで一番数学に魅力を感じたし、やらなかったことを後悔しています。
全国の大学受験生の大半はこの大会の出場校目指してるんだなぁhttps://t.co/Fi37FqIKb3
— よういち (@Work0827Yamanoi) 2018年8月8日
全国の一流インテグラーが集まって作ったおっぱいは、もはやグラフの垣根を超えて**芸術の域**に達していることでしょう。
参加大学一覧
~~※本当に積分しているかは不明~~
そのおっぱい、Pythonで再現できるんじゃね?
※学習の一環で行なっているから、決して下心はないんだからねっ!
数学を学習するきっかけを得たので無駄にすることはできません。早速グラフの製作に取り掛かります。スケベも学習も行動力が大事😏
実際の数式こと、おっぱい関数はこんな感じ↓
引用元:おっぱい関数 by CHARTMAN
指数関数やネイピア数が多用されていても問題なし、Pythonはデータ分析(とおっぱい分析)に特化した言語ということを忘れてはいけません!
卍numpy最強卍
今回は式がめちゃくちゃ長いので、変数に分割した式を代入してから結合する流れで作ります。
厳選した5つのおっぱい関数を再現してみた
以下、私が独断と偏見でセレクトしたおっぱい達をご覧あれ。
各大学から寄せられたコメントもハイレベルのため必見です。
文教大学
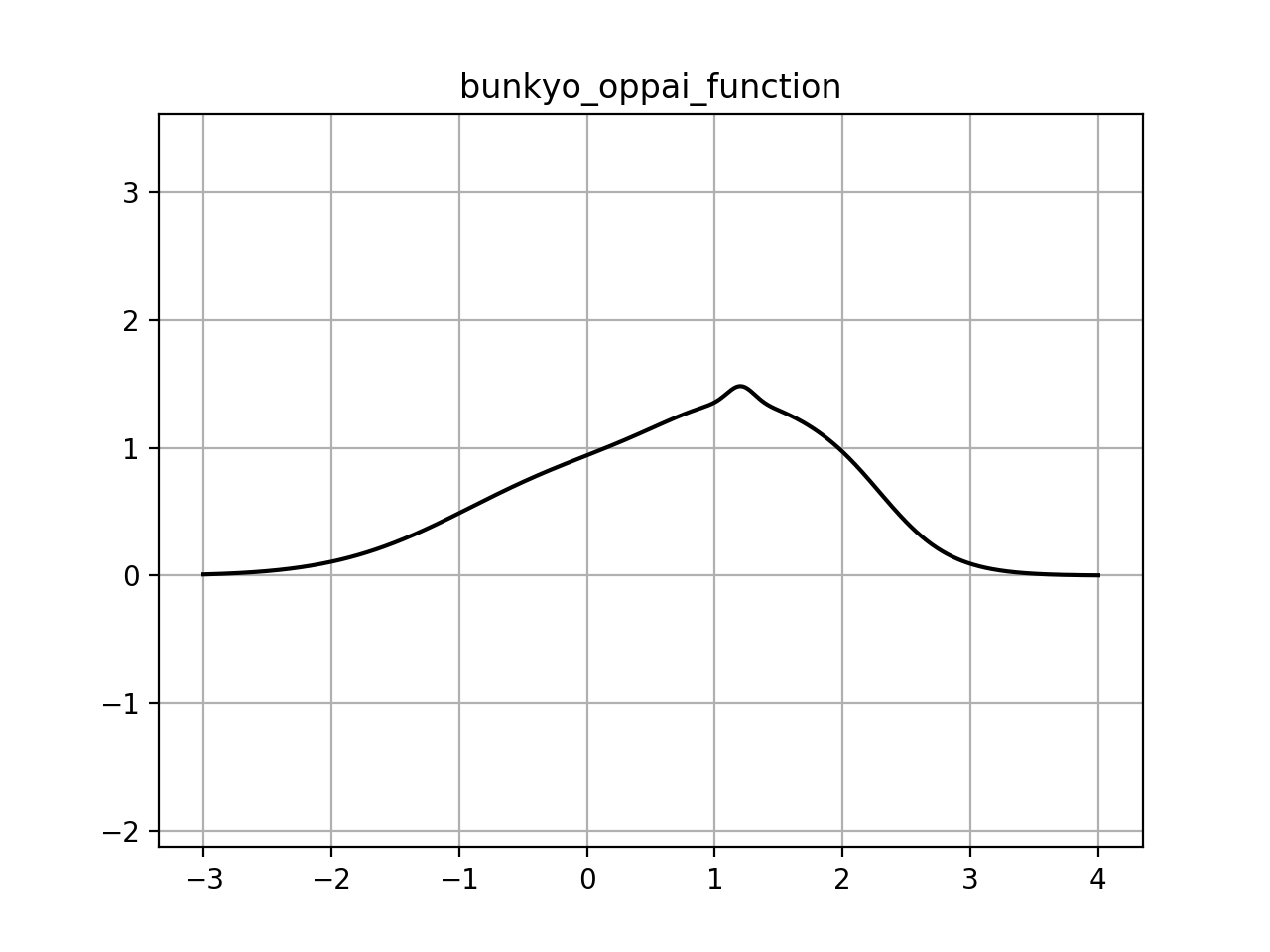
おっぱい関数
#### コメント 私の大学は先生になる人が全国的に見ても多い大学です。この関数によって**性に目覚め始めた小中学生がより良いおっぱい人生を歩めるよう教えたい**です。ちなみに**私は小さい胸を気にしている娘をいじめるのが好き**です。
初っ端から事々案々なコメントが寄せられました。現役学生かOBのどちらが製作したか不明ですが、後者ならかなりの事件性を感じます。
import numpy as np
import matplotlib.pyplot as plt
def bunkyo_oppai(x):
e = np.e
y_1 = (0.8 * (e ** ((-x ** 2) / 2)))
y_2 = (e ** (-(x - 1.4) ** 2))
y_3 = ((1 / 6) * (e ** (-(2 * x - 4.17) ** 2)))
y_4 = ((1 / 8) * (e ** (-(6.9 * x - 8.3) ** 2)))
y = y_1 + y_2 + y_3 + y_4
return y
def plot_oppai(x, y):
plt.title('bunkyo_oppai_function')
plt.axes().set_aspect('equal', 'datalim')
plt.grid()
plt.plot(x, y, 'black')
plt.show()
def main():
x = np.arange(-3, 4 + 0.01, 0.01)
y = bunkyo_oppai(x)
plot_oppai(x, y)
if __name__ == '__main__':
main()
実行結果
名古屋大学
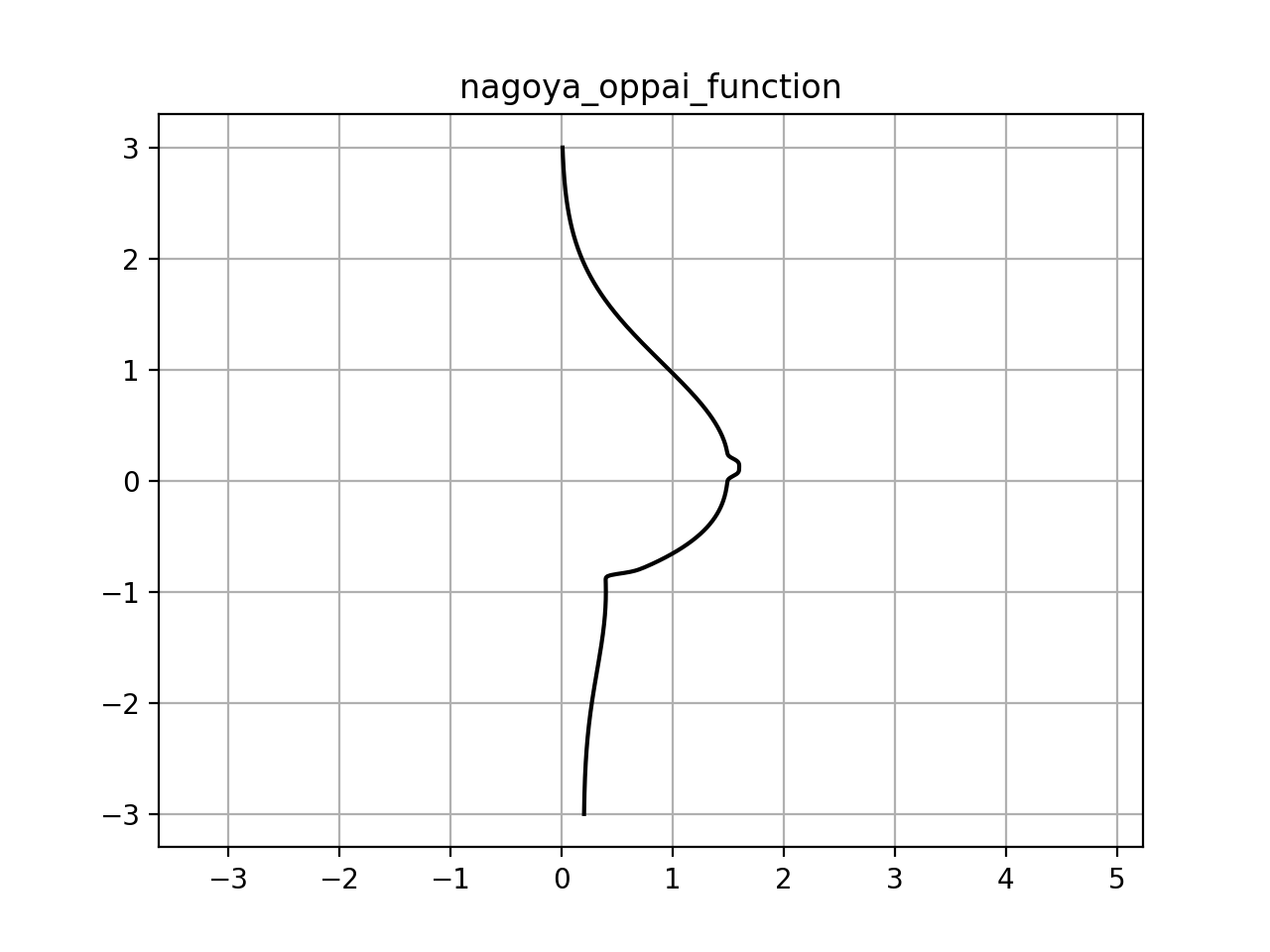
おっぱい関数
#### コメント **揺れない乳は乳と呼べません**。tを変数とする正弦関数を式中に含ませることで、滑らかな揺れを再現しました。単に平行移動するのではなく、**弾力のある乳がしなやかに動く**様子をお楽しみいただけることでしょう。
文教大学に引き続き素晴らしいコメントですね。個人的には揺れるギミックが備わっているうえに形が一番好みです。
このおっぱい関数を製作した学生さんは2D・3Dのグラフ製作に精通しており、たけのこの里やポンデリングを数式で再現しているツワモノです。興味のある方は参照してみてください。
import numpy as np
import matplotlib.pyplot as plt
def nagoya_oppai(y):
x_1 = (1.5 * np.exp(-0.62 * (y - 0.16) ** 2)) / (1 + np.exp(-20 * (5 * y - 1)))
x_2 = (1.5 + 0.8 * (y - 0.2) ** 3) * (1 + np.exp(20 * (5 * y - 1))) ** -1
x_3 = (1 + np.exp(-(100 * (y + 1) - 16)))
x_4 = (0.2 * (np.exp(-(y + 1) ** 2) + 1)) / (1 + np.exp(100 * (y + 1) - 16))
x_5 = (0.1 / np.exp(2 * (10 * y - 1.2) ** 4))
x = x_1 + (x_2 / x_3) + x_4 + x_5
return x
def plot_oppai(x, y):
plt.title('nagoya_oppai_function')
plt.axes().set_aspect('equal', 'datalim')
plt.grid()
plt.plot(x, y, 'black')
plt.show()
def main():
y = np.arange(-3, 3 + 0.01, 0.01)
x = nagoya_oppai(y)
plot_oppai(x, y)
if __name__ == '__main__':
main()
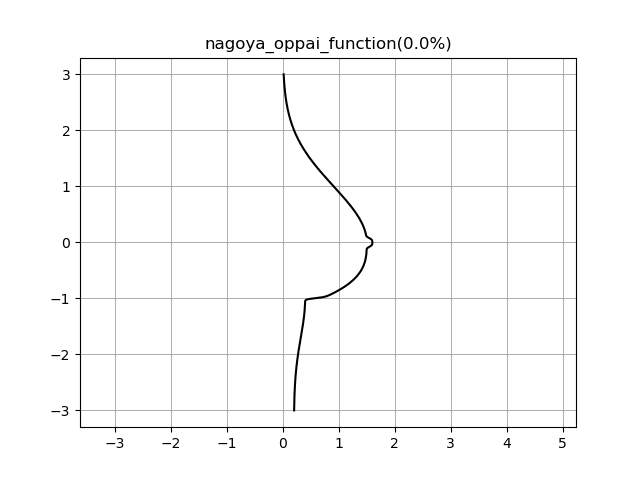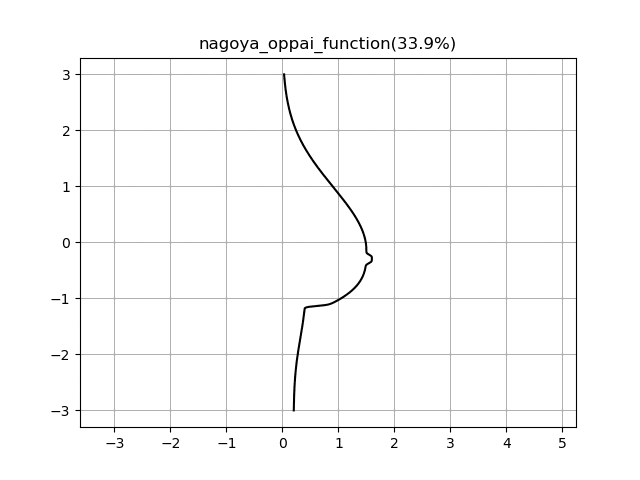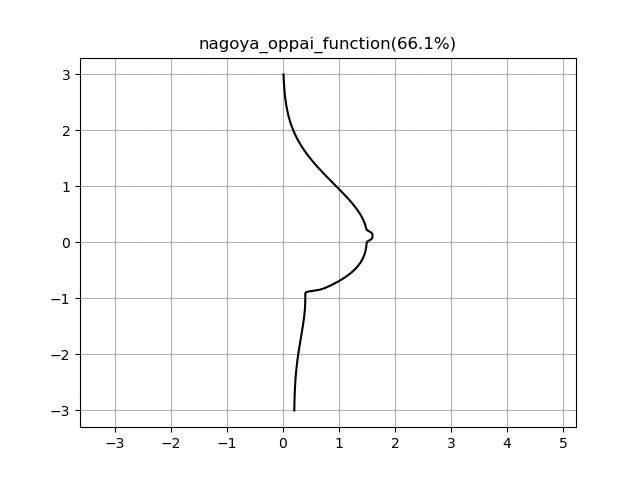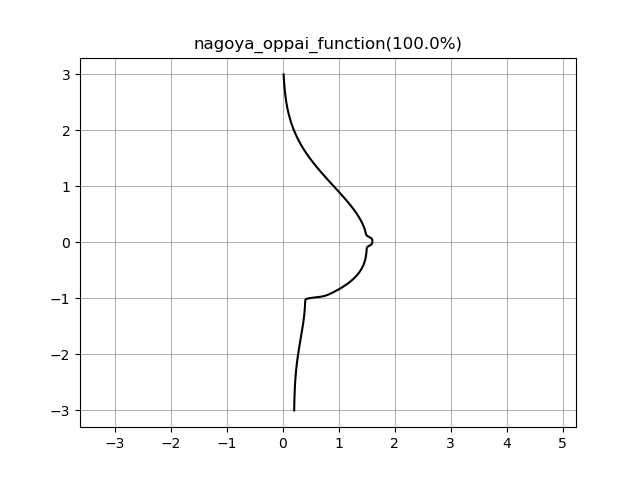
実行結果(static)
コメントに記載されている通り、tを変数とした正弦関数を含んだ式に変更することでブルンブルンするおっぱいを作ることが出来ちゃうんです。
月の重力並みにゆっくり揺れるので長い目で観察してくださいね。
実行結果(dynamic)
大阪大学
おっぱい関数
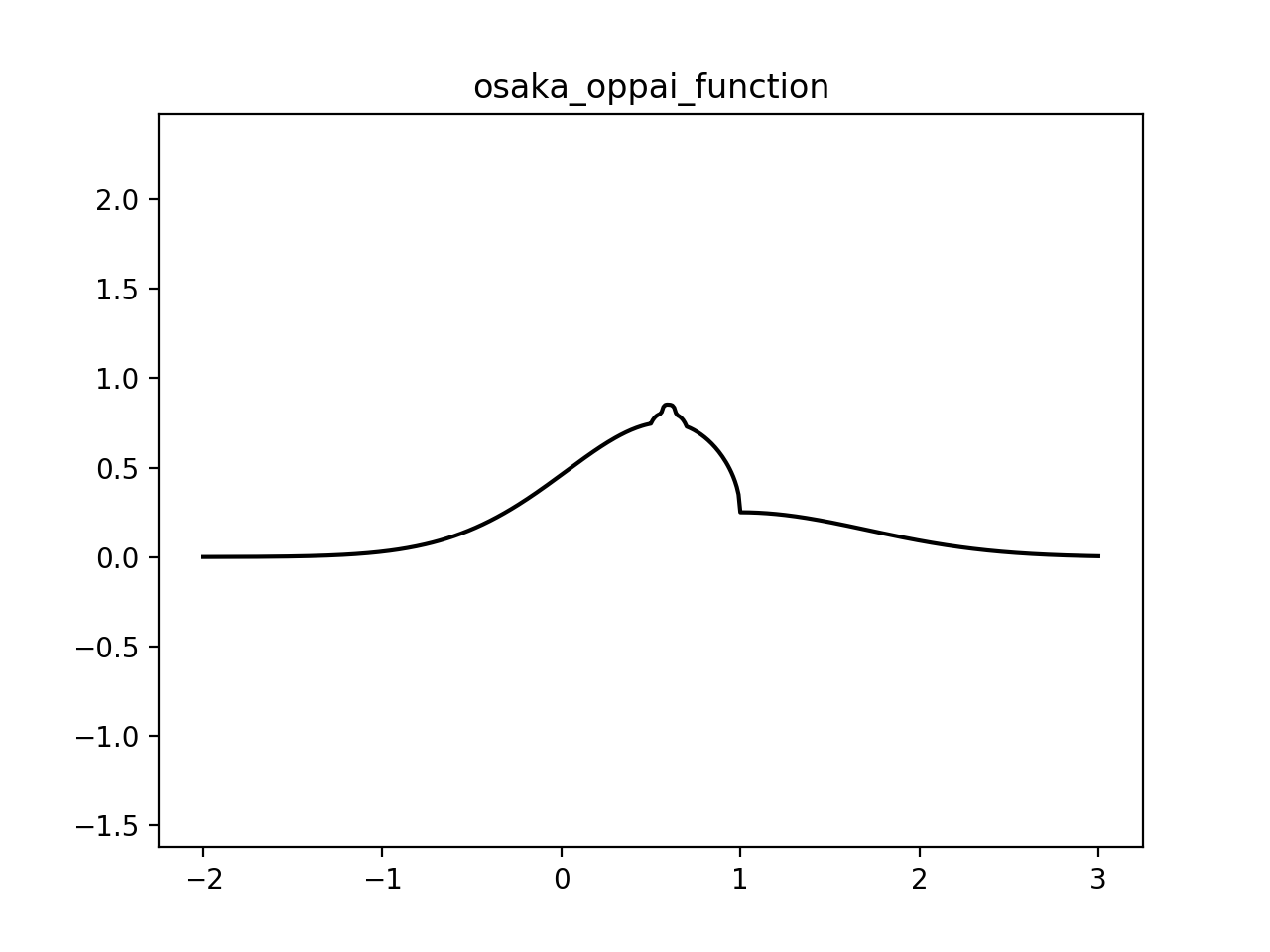
#### コメント 今回は優秀な曲線美をもつ√xe^(-x^2)を元に関数を作成しました。この関数の特徴は**単位おっぱい関数、即ち主要部が縦横共に±1を基準に存在している点**です。この関数で入賞することを祈ります。
やってきました。はなおさんと本家積分サークルメンバー率いる大阪大学の登場です。
特徴的な乳輪を再現しているのが素晴らしい。手を置くなら**微分不可能な点(下乳辺り)**で揺らしたいですね。
import numpy as np
import matplotlib.pyplot as plt
def osaka_oppai(x):
e = np.e
y_1 = ((np.sqrt((np.absolute(1 - x) + 1 - x) / 2) + (1 / 4)) * np.exp(-(1 - x) ** 2))
y_2_1 = (1 / 40)
y_2_2 = (np.absolute(1 - 2 ** 4 * (5 * x - 3) ** 4))
y_2_3 = (np.absolute(1 - 2 ** 9 * (5 * x - 3) ** 4))
y_2_4 = (2 - 528 * (5 * x - 3) ** 4)
y_2 = (y_2_1 * (y_2_2 + y_2_3 + y_2_4))
y = y_1 + y_2
return y
def plot_oppai(x, y):
plt.title('osaka_oppai_function')
plt.axes().set_aspect('equal', 'datalim')
plt.plot(x, y, 'black')
plt.show()
def main():
x = np.arange(-2, 3 + 0.01, 0.01)
y = osaka_oppai(x)
plot_oppai(x, y)
if __name__ == '__main__':
main()
実行結果
首都大学東京
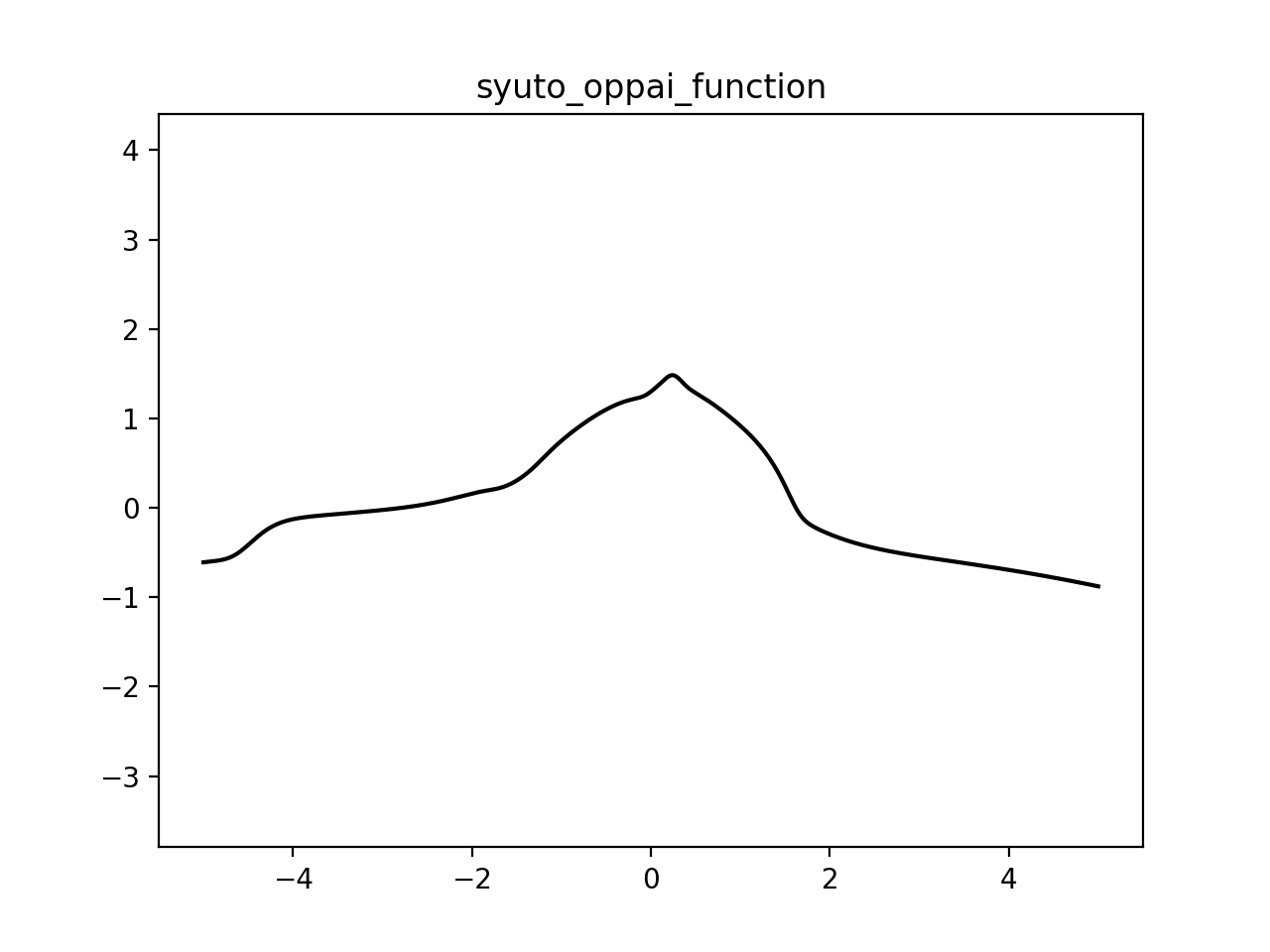
おっぱい関数
#### コメント y>0の範囲がおっぱいですが、おっぱいは**女の子についてこそ美しい**のでその周囲も関数で表現しました。**点(-4,0)近傍の鎖骨がポイント**です。
こちらのおっぱい関数は大阪大学に似ていますが、細かい所で大きな違いがあります。
何と言っても鎖骨が素晴らしい!そこに着眼点を置いたのは生粋のおっぱい好きの証ですね。私が保証します。
お腹の凹み具合も好き。
import numpy as np
import matplotlib.pyplot as plt
def syuto_oppai(x):
y_1 = (1.2 * np.exp(-0.5 * x ** 2))
y_2 = (np.exp(0.1 * x) - 1.3 ** (0.6 * x) - 1.1 ** -x)
y_3 = (0.2 * np.exp(-7 * (x - 0.8) ** 8))
y_4 = (0.1 * np.exp(-(8 * x - 2) ** 2) - 1.1 ** (x - 6))
y_5 = (0.4 * np.exp(-0.04 * x ** 8))
y_6 = (0.4 * np.exp(-0.04 * (x + 3) ** 8))
y_7 = (1.2)
y = y_1 + y_2 + y_3 + y_4 + y_5 + y_6 + y_7
return y
def plot_oppai(x, y):
plt.title('syuto_oppai_function')
plt.axes().set_aspect('equal', 'datalim')
plt.plot(x, y, 'black')
plt.show()
def main():
x = np.arange(-5, 5 + 0.01, 0.01)
y = syuto_oppai(x)
plot_oppai(x, y)
if __name__ == '__main__':
main()
実行結果
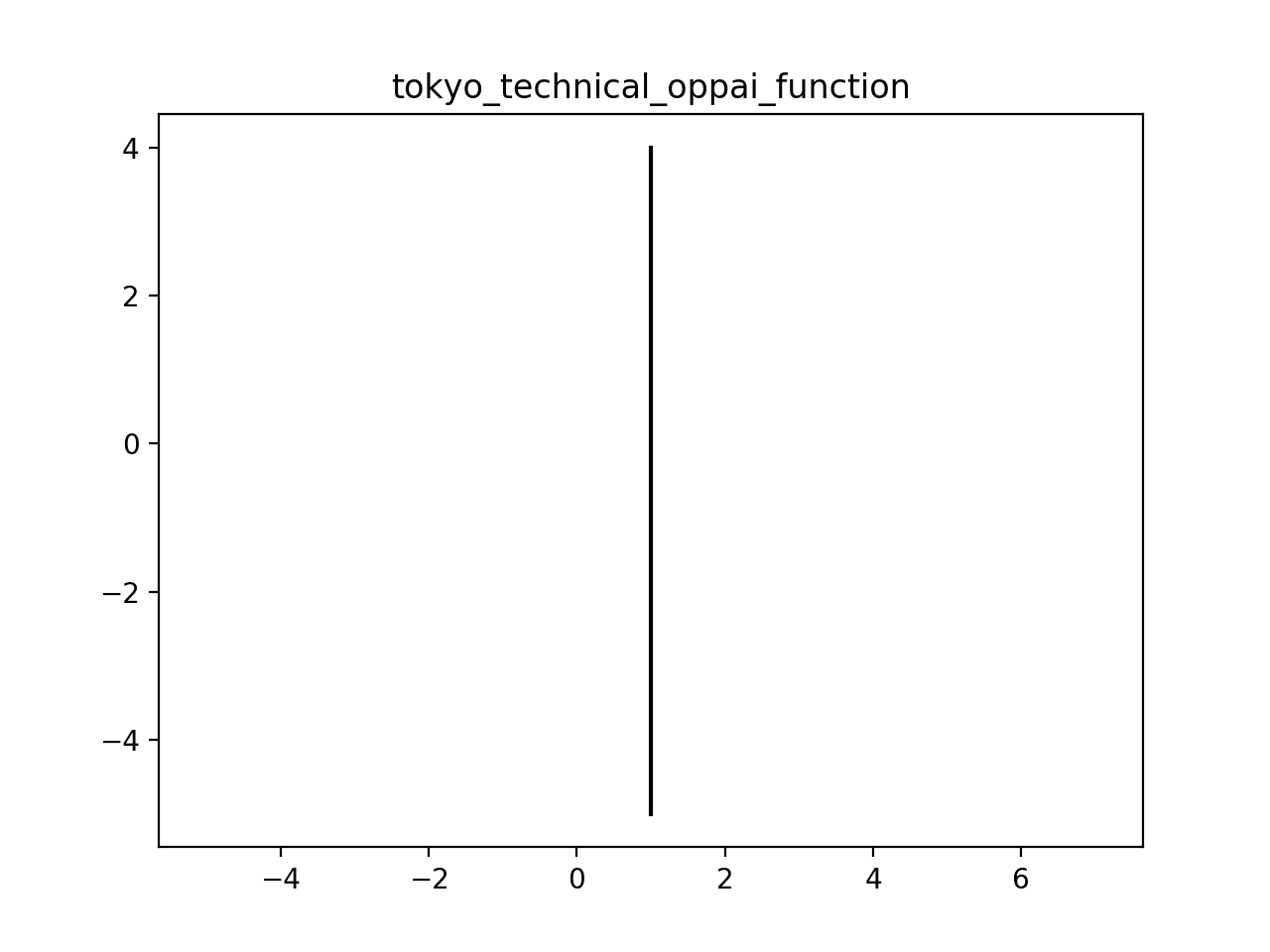
東京工科大学
おっぱい関数
#### コメント 我々の大学はFラン大学もいい所、所詮底辺大学です。しかし、**貧乳および無乳の魅力にはどこ大学生だろうが大学生で無かろうが関係ありません**。私たちは貧乳及び無乳の方々が微小ながらも頑張るその努力に萌えるのです。我々は**この華麗で簡素で研ぎ澄まされた関数**こそ貧乳派を語る上での第一関門を提唱します。
ネタπ部門から一つ選ばせていただきました。
他の作品を選ぼうにも、まな板やレーズンといった数式に表せないものばかりだったので半分仕方ない感じでした(まな板とレーズンに限る意見をお持ちの方はごめんなさい)。
コーディング時間は3分と、まさに爆速おっぱい。
import numpy as np
import matplotlib.pyplot as plt
def get_coord():
x = np.ones(10)
y = np.arange(-5, 5, 1)
return x, y
def plot_oppai(x, y):
plt.title('tokyo_technical_oppai_function')
plt.axes().set_aspect('equal', 'datalim')
plt.plot(x, y, 'black')
plt.show()
def main():
x, y = get_coord()
plot_oppai(x, y)
if __name__ == '__main__':
main()
実行結果
まとめ
紹介していない大学も複数ありますが、それぞれの大学~~**(ではなく所属する学生個人)**~~の性癖を垣間見ることが出来たと思います。因みに私は名古屋大推し
絶賛夏休み期間中ですので、自由研究の参考になれば幸いです(