【時系列波形異常検知 part2】DAMPによる時系列ディスコードの探索 (Python実装例付)

[TL;DR] 以下の論文紹介とpython実装: Lu, et al. "Matrix profile XXIV: scaling time series anomaly detection to trillions of datapoints and ultra-fast arriving data streams.",KDD2022.

§1. はじめに

前回は単変量時系列異常検知にて最強 [1] [2] の時系列ディスコード(Time Series Discords)の紹介と、その探索アルゴリズムとしてDRAG [3] を紹介しました。

しかしながら、DRAGは2007年に提案された方法であり、しばしばレトロ感があるため、今回は時系列ディスコード探索における令和最新版のDAMP(Discord Aware Matrix Profile) [4] と呼ばれるアルゴリズムを紹介します。名前からお察しの通り、DAMPは以前紹介したMatrix Profileのファミリーです。

時系列ディスコード再掲↓

とはいえ、私のPython実装だとDRAGより遅い結果になりました。アルゴリズム理解のため原著[4]での記述の忠実な再現を優先した結果、若干非効率な実装になってるようです。

§2. DAMP

DAMPでは、時系列ディスコードの定義が以前と少し異なり、自身の過去の部分時系列に関し、類似した部分時系列が存在しないもの（最近傍との距離が極めて大きいもの）をディスコードとします。DRAGのときは自身の未来に出現する部分時系列も近傍対象だったので、探索する範囲が狭くなりました。異常検知の考え方からすると未来の時系列は考えないというのは理にかなっていると言えるでしょう。

DAMPアルゴリズムでは、①Backward Processingと②Forward Processingの2つのフェーズを繰り返します。①Backward Processingでは、現在注目している1つの部分時系列がディスコードかどうかを計算します。②Forward Processingでは、現在注目している部分時系列の将来の部分時系列について、ディスコードになり得るかどうかを計算し、なり得ないものをプルーニングします。

にて②Forward Processingでは、現在注目してる1つの部分時系列とその未来の全ての部分時系列に対して距離を調べ、現時点で最大のディスコードスコア（=最近傍距離）を下回るなら、その未来の部分時系列は今後の探索対象から除外します。

疑似コード

	処理	結果
1	For i = テスト期間開始 to 時系列の最後
2	iが探索対象外インデックスならスキップ
3	$T_{i:i+m-1}=[T_i,T_{i+1},...,T_{i+m-1}]$についてBackward Processing	現在のBestディスコードスコアを取得
4	$T_{i:i+m-1}=[T_i,T_{i+1},...,T_{i+m-1}]$についてForward Processing	探索対象除外インデックス作成

§2.1 Backward Processing

このフェーズでは、現在注目してる1つの部分時系列とその最近傍を算出します。その最近傍が現在調べたディスコード候補よりディスコードスコア（単に最近傍との距離のことです）が大きい場合はそれを更新します。

基本的には現在注目している、時系列の$i$番目から開始する部分時系列$T_{i:i+m-1}=[T_i,T_{i+1},...,T_{i+m-1}]$（ただし$m$は部分時系列の長さ、ハイパラ）と、その過去の時系列$T_{1:i}$の全ての部分時系列との距離を地道に計算する訳ですが、ここで計算を高速化するテクニックが2つ盛り込まれています。

• MASSと呼ばれる、高速フーリエ変換を利用した部分時系列の距離計算アルゴリズムを用います。Matrix Profileファミリーでお馴染みの方法のため今回は説明を割愛します。

• 最初は$T_{i:i+m-1}$の近くのある範囲の時系列から検索を開始し、現在調べた中で最大のディスコードスコア：BSFよりスコア（=最近傍距離）が小さい部分時系列を発見したら検索を直ちに中止します。これは、最近傍は必ずこのスコアより小さくなるため、それがBSFを下回るのであればBSFの更新の見込みがない（ディスコード足り得ない）訳です。逆に、最後まで検索してなおBSFを下回らないのであれば、そいつが現在調べた範囲の最有力ディスコード候補であり、BSFが更新されます。

以下、Backward ProcessingのPython実装です。

import numpy as np
from numba import njit
from numpy.fft import fft, ifft

@njit
def DAMP_backward_processing(T, m, i, best_so_far):
    """
    Parameters
    T : 1D time series data 
    m : Subsequence length
    i : Index of current query
    best_so_far : Highest discord score so far
    Returns
    aMPi : Discord value at position i
    best_so_far : Updated best_so_far
    """
    aMPi = np.inf
    prefix = int(2**nextpow2(m))
    while aMPi >= best_so_far:
        if i - prefix <= 0:
            aMPi = min(MASS(T[:i], T[i:i+m]).real)
            if aMPi > best_so_far:
                best_so_far = aMPi
            break
        else:
            aMPi = min(MASS(T[i-prefix:i], T[i:i+m]).real)
            if aMPi < best_so_far:
                break
            else:
                prefix = int(2 * prefix)
    return aMPi, best_so_far

時系列の$i$番目について上述した処理を行い、現在のディスコードスコアの推定値aMPiと、BSF(best_so_far)を調べる感じです。推定値aMPiとは、BSFの更新があった場合は$T_{i:i+m-1}$とその過去の時系列$T_{1:i}$の全ての部分時系列との距離の正確な最近傍値ですが、更新がなかった場合はBSF以下の何かしらの値です。BSF以下の値には興味がありません。高速化テクその2における検索範囲は2のべき乗のサイズで順に広げていきます。その方がFFTの計算に都合がよいからです。

§2.2 Forward Processing

②Forward Processingでは、現在注目してる部分時系列$T_{i:i+m-1}$とその未来の全ての部分時系列に対して距離を調べ、BSFを下回る部分時系列が存在すれｂ、その未来の部分時系列は今後の探索対象から除外します。前述した高速化テクその2で述べた考え方同様、適当な部分時系列との距離ですらBSFを下回るなら、最近傍はもっとスコア（=最近傍距離）が低いはずなのでもうその部分時系列はディスコード足り得ず、興味がないのです。

計算上は、各部分時系列についてプルーニング値：PVを定義してやり、興味を失った未来の部分時系列はそれが0になります。

以下、Forward ProcessingのPython実装です。

@njit
def DAMP_forward_processing(T, m, i, best_so_far, PV):
    """
    Parameters
    T : 1D time series data 
    m : Subsequence length
    i : Index of current query
    best_so_far : Highest discord score so far
    PV : Pruned Vector
    Returns
    PV : Updated PV
    """
    if i + m >= len(T) - m + 1:
        return PV
    lookahead = int(2**nextpow2(m))
    start = i + m
    end = min(start + lookahead, len(T))
    D_i = MASS_njit(T[start:end], T[i:i+m]).real
    indexes = np.where(D_i <= best_so_far)[0] + start
    PV[indexes] = 0
    return PV

§2.3 メインアルゴリズム

前述した疑似コードを元にPythonで書くと次のようになります。

@njit
def DAMP(T, m, spIndex):
    """
    DAMP algorithm for time series discords discovery.
    
    Parameters
    T : 1D time series data 
    m : Subsequence length
    spIndex : Location of split point between training and test data
    Returns
    aMP : Left approximate Matrix Profile
    """
    aMP = np.zeros(len(T)-m+1)
    best_so_far = 0.
    PV = np.ones(len(T)-m+1)
    for i in range(spIndex, len(T)-m+1):
        if PV[i] == False:
            aMP[i] = aMP[i-1]
        else:
            aMP[i], best_so_far = DAMP_backward_processing(T,m,i,best_so_far)
            PV = DAMP_forward_processing(T,m,i,best_so_far,PV)
    return aMP

出力のaMPというのは各インデックスのディスコードスコアであり、これの最大値を取る位置がディスコードの位置となります。

§3. Pythonでの異常検知実施例

§3.1 いつものECGデータ

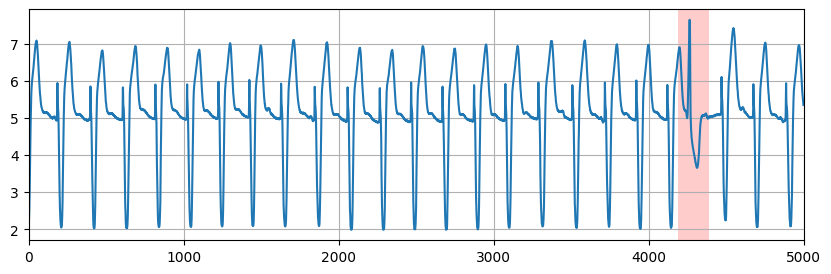
今日もECG時系列データを擦っていきます。
https://www.cs.ucr.edu/~eamonn/discords/qtdbsel102.txt

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from damp import *

#データの読み込み
ECG = pd.read_csv('qtdbsel102.txt', header=None, delimiter='\t')    
X = ECG.values[:5000,2]

#ハイパラ
w_size = 200 # 窓幅
train_term = 2000 # 0点～2000点目が学習期間

#DAMPアルゴリズムの適用
approximate_matrix_profile = DAMP(X, w_size ,train_term)
top_1_discord_start_point = approximate_matrix_profile.argmax()

#ECG dataとdiscord可視化
plt.figure(figsize=(10, 3))
plt.grid()
plt.plot(X)
plt.axvspan(top_1_discord_start_point,
             top_1_discord_start_point+w_size, facecolor='r', alpha=0.2)
plt.xlim(0,5000)

このデータはQiita上で何度も紹介してるので小並感で失礼しますが、今回も上手くいきました。

§3.2 アカボウクジラに取り付けられた加速度センサデータ

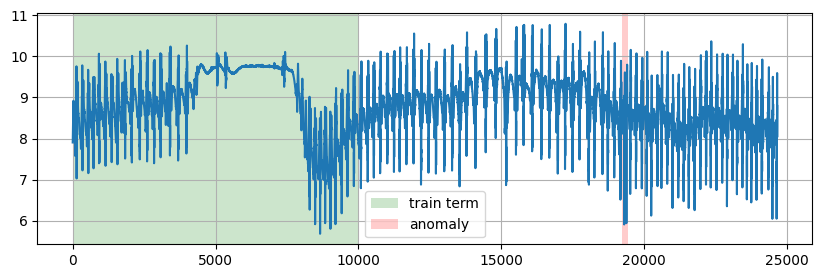
たまには別のデータでも試してみましょう。KDD2021のコンペで登場した単変量時系列異常検知データセットなるものがありまして、今回はその中から「アカボウクジラに取り付けられた加速度センサデータ」とか言う謎データでやってみましょう。
https://www.cs.ucr.edu/~eamonn/time_series_data_2018/UCR_TimeSeriesAnomalyDatasets2021.zip

#データの読み込み
X=pd.read_csv('UCR_Anomaly_FullData/151_UCR_Anomaly_MesoplodonDensirostris_10000_19280_19440.txt', header=None, delimiter='\t').values.reshape(-1,)


#ハイパラ
w_size = 200 # 窓幅
train_term = 10000 # 0点～10000点目が学習期間

#DAMPアルゴリズムの適用
approximate_matrix_profile = DAMP(X, w_size ,train_term)
top_1_discord_start_point = approximate_matrix_profile.argmax()

#時系列とdiscord可視化
plt.figure(figsize=(10, 3))
plt.grid()
plt.plot(X)
plt.axvspan(0,10000, train_term='green', alpha=0.2,label="train term")
plt.axvspan(top_1_discord_start_point,
             top_1_discord_start_point+w_size, facecolor='r', alpha=0.2,label="anomaly")
plt.legend()

クジラの謎データでも無事異常検出を確認出来ましたね。
DAMPの有効性が強調されました👍

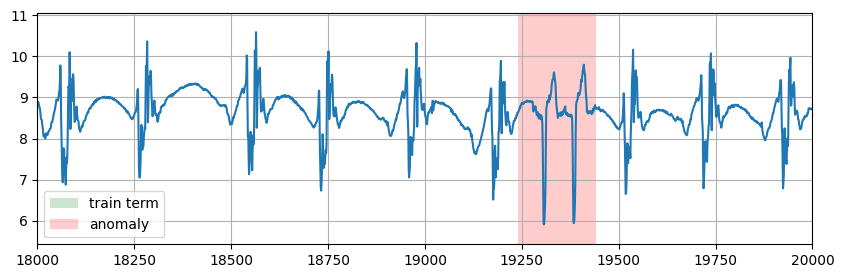
目が悪くて確認出来なかった方のために、上の図を拡大したやつも置いておきます↓

§4. 議論

著者のオリジナルのプログラム（MATLAB）が公開されているのですが、原著[4]から随分改良が加えられていた様子でした。一方、本実装は論文理解のため、原著[4]に記載のアルゴリズムを忠実に再現しました。参照出来るものがなかったため、オリジナルコードの改良を全ては解読出来ませんでしたが、自分で実装して一つ気付いたのは、backward_processing内の計算する範囲

MASS(T[i-prefix:i], T[i:i+m]) 

のT[i-prefix:i]の部分が次のイテレーション時も一部重複してるので、重複範囲は省略出来るんじゃないのかな思いました。（←じゃあ改良したコードも紹介しろ。TBD。）

§5. おわりに

本記事では、時系列異常検知に役立つ時系列ディスコードの探索に関する最先端のアルゴリズムDAMP(Discord Aware Matrix Profile)を紹介しました。
DAMPはMatrix Profileのファミリーなので、Matrix Profile関連の基礎概念（特にMASSアルゴリズム）については本記事では省略しましたが、プログラムを動作させるための全ての実装はgithubをご確認ください。

最近みつけたrocket-fftとかいうマイナーなライブラリで高速化してます。ご照覧あれ。

著者のオリジナルプログラムはこちらです。

参考文献

[1] Wu, Renjie, and Eamonn J. Keogh. "Current time series anomaly detection benchmarks are flawed and are creating the illusion of progress." IEEE transactions on knowledge and data engineering 35.3 (2021): 2421-2429.
[2] Nakamura, Takaaki, et al. "Merlin: Parameter-free discovery of arbitrary length anomalies in massive time series archives." 2020 IEEE international conference on data mining (ICDM). IEEE, 2020.
[3] Yankov, Dragomir, Eamonn Keogh, and Umaa Rebbapragada. "Disk Aware Discord Discovery: Finding Unusual Time Series in Terabyte Sized Datasets." Seventh IEEE International Conference on Data Mining (ICDM 2007). IEEE, 2007.
[4] Lu, Yue, et al. "Matrix profile XXIV: scaling time series anomaly detection to trillions of datapoints and ultra-fast arriving data streams." Proceedings of the 28th ACM SIGKDD conference on knowledge discovery and data mining. 2022.