前回はkintoneの標準機能で自然対数を求めてみました。
ただ、前回の内容だと底は$ e $限定、真数$ X $は$ 0<X\leqq2 $の範囲にしか対応していないので、
もっと自由度を高めたいところです。
というわけで、まずは真数$ X $の範囲をできるだけ大きくできるように工夫したいと思います。
真数Xを大きくする方針
$ log_eX $において$ X = x^n $ とおくと、
$ log_eX = log_ex^n = nlog_ex $ となります。
$ x = X^\frac{1}{n} $ なので、真数$ X $を$ \frac{1}{n} $ 乗した数 $ x (x > 0) $ を真数とする $ log_ex$ を求めて $ n $ 倍すれば、
進数 $ X>2 $ の自然対数を求めることができるはず。
というわけで、
1. Xのn乗根($ X $ の $ \frac{1}{n} $ 乗)を求めるアプリ(今回)
2. 真数 $ X>2 $ の自然対数 $ lnX $ を求めるアプリ
3. $ log_aX $ を求めるアプリ
の順に作っていきます。
今回はXのn乗根を求めるアプリを作成します。
Xのn乗根を求めるアプリ
kintoneの数式には整数でべき乗する演算子はありますが、$ \frac{1}{n} $ 乗( $ n $ は整数)できる演算子がありません。
なので、計算フィールドを使ってちょっと工夫して計算する必要があります。
理屈はいいやって方は「アプリを作る」まで飛ばしてね。
ニュートン法でn乗根を求める
ニュートン法については
kintoneのアプリでニュートン法で平方根を求める方法についての過去記事でちょっと説明しました。
今回は平方根ではなくて、n乗根です。とはいえ、そんなに方法は変わらないので、
上記記事の式③を利用して計算したいと思います。
※元の式のnは「n番目」のnですが、n乗根のnとの混同を防ぐためkに変えてみました。
f'(x_k) = \frac{f(x_k)}{x_k-x_{k+1}} ・・・・③
$ X $ のn乗根を求めたいので、$ f(x) = x^n - X = 0 $ の解を求めるとします。
\ f(x) = x^n - X\\
\ f'(x) = nx^{n-1} \\
より、③の式に代入すると $ x_{k+1} $ と $ x_k $ の関係は
\begin{align}
nx_k^{n-1} &= \frac{x_k^n - X}{x_k-x_{k+1}}\\
x_k-x_{k+1} &=\frac{x_k^n - X}{nx_k^{n-1}}\\
x_{k+1} &=\frac{-x_k^n + X}{nx_k^{n-1}} + x_k\\
よって、\\
x_{k+1}&=\frac{n-1}{n}x_k + \frac{X}{nx_k^{n-1}}
\end{align}
となります。
これをアプリの数式に入れていきます。
アプリを作る
アプリを作る準備
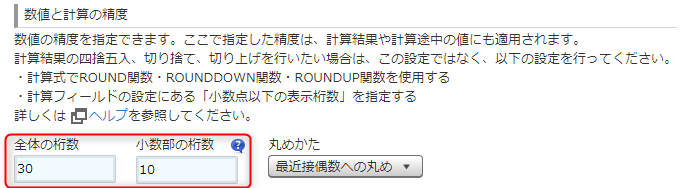
数値と計算の精度の桁数は
全体の桁数:30
小数部の桁数:10
にしておきましょう。
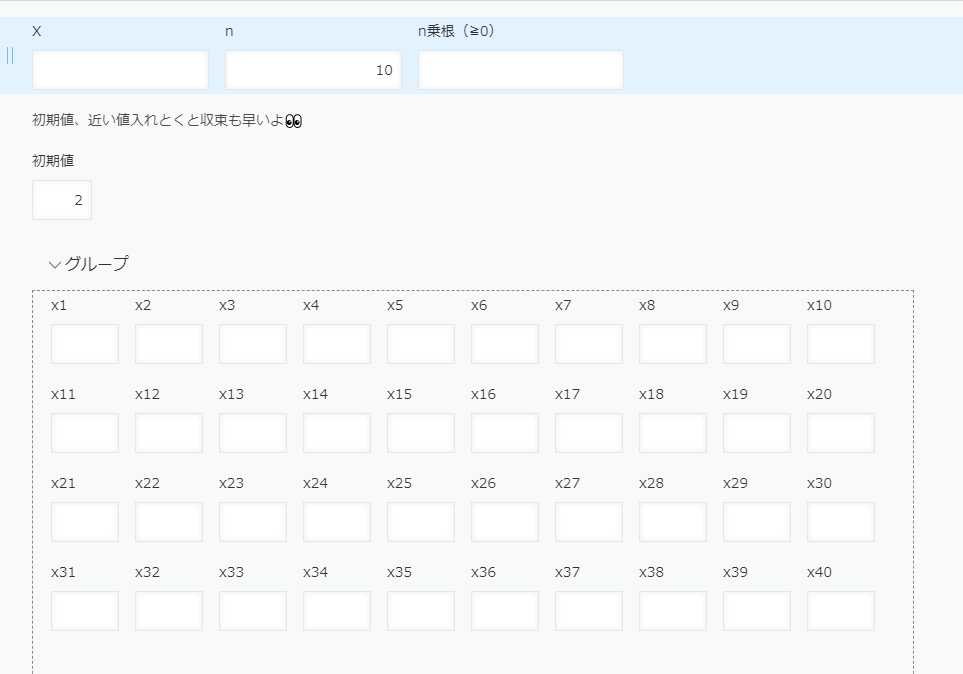
フィールドの設定
フィールド数も多くて、ちょっと大変です。
x1~x41は 20個くらいでも良いかもしれないです。
アプリ名は**Xのn乗根(ニュートン法)**としておきましょう。
※後でルックアップしてくるときに使います。
| フィールド種類 | フィールド名 | フィールドコード | 数式 | 備考 |
|---|---|---|---|---|
| 数値 | X | X | n乗根を求めたい値 | |
| 数値 | n | n | 何乗根にしたいか。デフォルト10 | |
| 計算 | n乗根(≧0) | x41 | ((n-1)/n)x40+X/(nx40^(n-1)) | 数値は$ x_k $ の$ k $の値。41回目で収束とする。 |
| 数値 | 初期値 | x0 | 初期値2にしてみました。 | |
| 計算 | x1 | x1 | ((n-1)/n)x0+X/(nx0^(n-1)) | |
| 計算 | x2 | x2 | ((n-1)/n)x1+X/(nx1^(n-1)) | |
| 計算 | xk | xk | ((n-1)/n)xk+X/(nxk^(n-1)) | x3~x39はkに番号入れてね |
| 計算 | x40 | x40 | ((n-1)/n)x40+X/(nx40^(n-1)) |
できあがり
こんな感じで計算します。