以前、標準機能で平方根を求める方法について書きました↓が、
https://qiita.com/juri_don/items/dd7b2d6ab4fb045990b6
今回は標準機能で三角関数のフィールドXに角度を入力したら、sinX,cosX,tanXを求める。というアプリを作ってみたいと思います👀!
kintoneのアプリ上で使う式
テーラー展開という関数を多項式で近似する方法がありまして、
sinX, cosXをx=0のまわりでテーラー展開すると
\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + ・・・\\
\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + ・・・
と近似することができます。
tanX は
\tan x = \frac{\sin x}{\cos x}
で求めます。
これらをkintoneの標準機能で計算してみたいと思います。
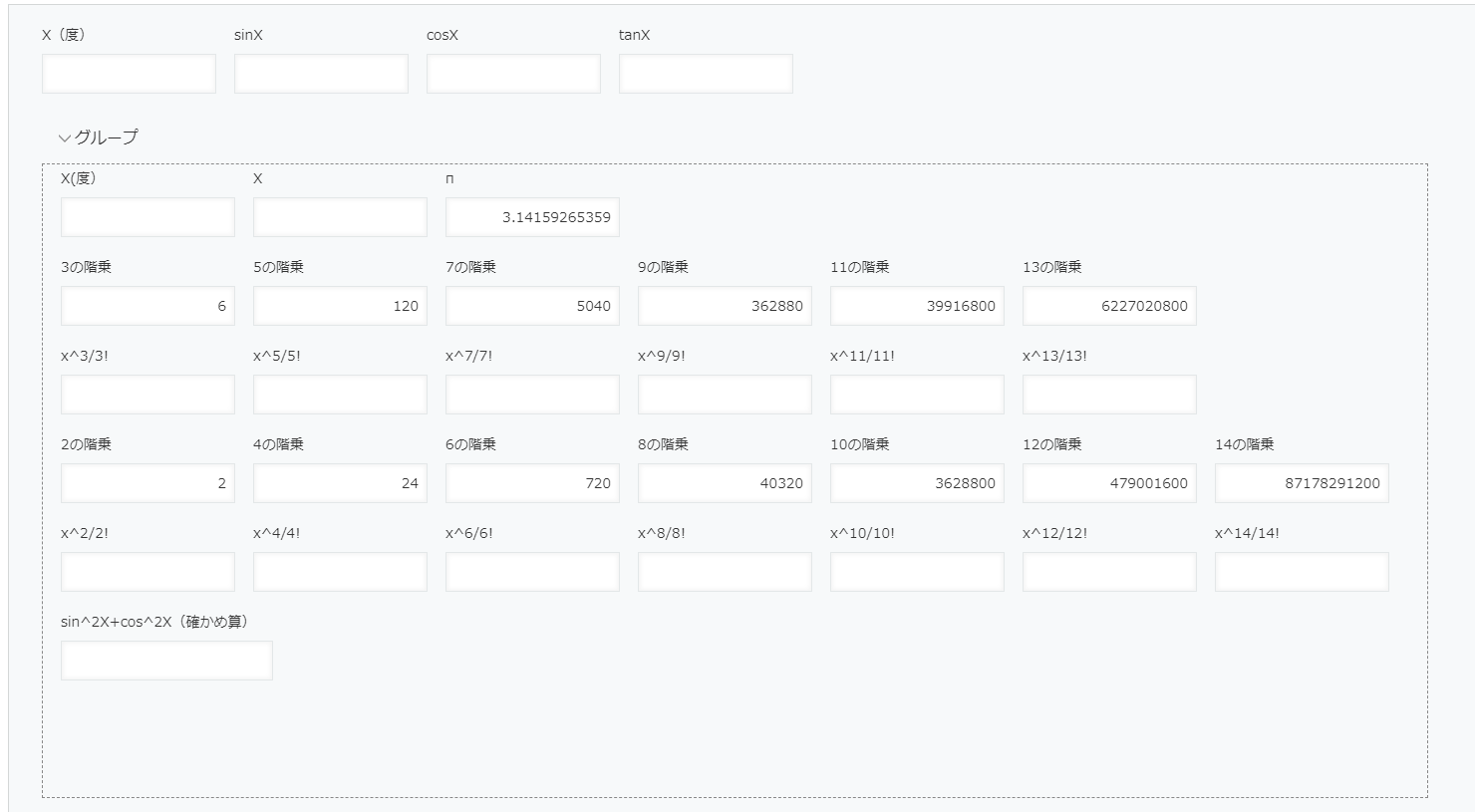
フォームの作成
ええと、作るの大変です👀
各フィールドの設定は、下の一覧表通りにやってね!
| フィールド種類 | フィールド名 | 計算式・初期値 | フィールドコード |
|---|---|---|---|
| 数値 | X(度) | 手入力 | Xdo_0 |
| 計算 | sinX | X-X3+X5-X7+X9-X11+X13 | sinX |
| 計算 | cosX | 1-X2+X4-X6+X8-X10+X12-X14 | cosX |
| 文字列(1行) | tanX | IF(cosX<>0,sinX/cosX,"∞") | tanX |
| 計算 | X(度) | Xdo_0 - ROUNDDOWN(Xdo_0/180)*180 | Xdo |
| 計算 | X | Xdo/180*π | X |
| 数値 | π | 3.14159265359 | π |
| 数値 | 2の階乗 | 2 | f2 |
| 数値 | 3の階乗 | 6 | f3 |
| 数値 | 4の階乗 | 24 | f4 |
| 数値 | 5の階乗 | 120 | f5 |
| 数値 | 6の階乗 | 720 | f6 |
| 数値 | 7の階乗 | 5040 | f7 |
| 数値 | 8の階乗 | 40320 | f8 |
| 数値 | 9の階乗 | 362880 | f9 |
| 数値 | 10の階乗 | 3628800 | f10 |
| 数値 | 11の階乗 | 39916800 | f11 |
| 数値 | 12の階乗 | 479001600 | f12 |
| 数値 | 13の階乗 | 6227020800 | f13 |
| 数値 | 14の階乗 | 87178291200 | f14 |
| 計算 | x^2/2! | x^2/f2 | X2 |
| 計算 | x^3/3! | X^3/f3 | X3 |
| 計算 | x^4/4! | X^4/f4 | X4 |
| 計算 | x^5/5! | X^5/f5 | X5 |
| 計算 | x^6/6! | X^6/f6 | X6 |
| 計算 | x^7/7! | X^7/f7 | X7 |
| 計算 | x^8/8! | X^8/f8 | X8 |
| 計算 | x^9/9! | X^9/f9 | X9 |
| 計算 | x^10/10! | X^10/f10 | X10 |
| 計算 | x^11/11! | X^11/f11 | X11 |
| 計算 | x^12/12! | X^12/f12 | X12 |
| 計算 | x^13/13! | X^13/f13 | X13 |
| 計算 | x^14/14! | X^14/f14 | X14 |
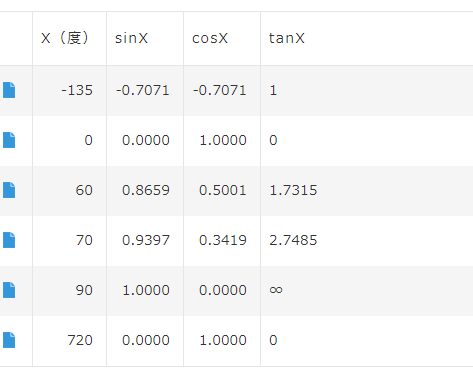
試してみる
なんとなく↓このあたりを試してみました。
0度、60度、90度、720度, -135度, 70度
↓こちらで確かめたら大体あっていました。だいたいですが。
https://keisan.casio.jp/exec/system/1260261251
まとめ
無理やり三角関数の計算をしてみました。
これをするくらいなら、素直にJavaScriptを書いたほうが早いし、精度も高いと思います。
しかしどうしても・・・というときはこれで三角関数(近似値)で計算できます👀試してみてね!
では今回はこのへんでノシノシ