LoginSignup
9
12

More than 5 years have passed since last update.

@junjis0203

数学ガールの秘密ノート／行列が描くもの 第4章を再現してみた

Last updated at Posted at 2018-11-25

はじめに

みなさん、数学ガールは読まれていますか？最新巻1はみんな大好き行列巻です。
数学ガールの秘密ノート／行列が描くもの

内容としては2x2行列が中心で、第4章では行列を用いた座標変換の話題になっています。
コンピュータ少女のリサが座標変換の様子をプログラムして表示するわけですが、Twitterの感想で「リサは何のプログラミング言語を使っているのだろう？」というものがありました。

ここまで前説。
というわけで、今回は秘密ノート行列編第4章に掲載されている図を「matplotlibを使って再現してみる」ということをしてみたいと思います。

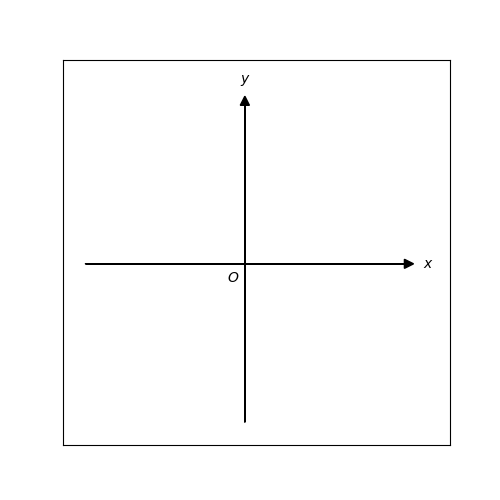
p.136 座標平面の表示

p.136ってのは書籍のページ番号です。以下同様。

とりあえずmatplotlibをimportします。どうせ必要になるだろうからnumpyもimportしておきます。

import matplotlib.pyplot as plt
import numpy as np

さて、一発目の図は座標平面ですがmatplotlibの表示を書籍に合わせるのは地味に大変です。まずはコードを提示。

def coordinate_plane(new_figure=True, alpha=1.0):
    if new_figure:
        plt.figure(figsize=(5, 5))

    plt.xticks([])
    plt.yticks([])

    plt.xlim(-4.0, 4.5)
    plt.ylim(-4.0, 4.5)

    # X軸とY軸
    plt.arrow(-3.5,    0, 7, 0, head_width=0.2, head_length=0.2, color='black', alpha=alpha)
    plt.arrow(   0, -3.5, 0, 7, head_width=0.2, head_length=0.2, color='black', alpha=alpha)

    plt.text( 3.9, -0.1, '$x$', alpha=alpha)
    plt.text(-0.1,  4.0, '$y$', alpha=alpha)

coordinate_plane()
plt.text(-0.4, -0.4, '$O$')

plt.show()

こんな感じになります。

Figure_1.png

座標平面描画を関数化しているのはこの後ずっと使うためです。new_figureとalphaの引数については最後の方で説明するのでひとまず無視してください。
それでは使ってる各関数について説明します。

figure 

plt.figure(figsize=(5, 5))

matplotlibのデフォルトの画面サイズは6.4x4.8インチでdpiが100なのでピクセルだと640x480になります。このままでは横長になってしまうので明示的にfigure関数をfigsize引数指定で呼び出して500x500の画面にします。

xticks, yticks 

plt.xticks([])
plt.yticks([])

目盛りは必要ないので空配列を渡して表示しないようにします。

xlim, ylim 

plt.xlim(-4.0, 4.5)
plt.ylim(-4.0, 4.5)

matplotlibではX範囲、Y範囲が自動的に設定されますが今回は範囲を固定しています。プラス方向に0.5長くしているのは軸のラベルを書くためです。
ちなみに、今回は点をプロットしてないのでこの指定をしないと座標平面が表示されないということになります（arrowやtextだけでは表示範囲は設定されない）

arrow 

plt.arrow(-3.5,    0, 7, 0, head_width=0.2, head_length=0.2, color='black', alpha=alpha)
plt.arrow(   0, -3.5, 0, 7, head_width=0.2, head_length=0.2, color='black', alpha=alpha)

これでX軸とY軸を書いています。
arrow関数の注意として、「(x1, y1)から(x2, y2)」という指定ではなく、「(x1, y1)から(dx, dy)分矢印を引く」と指定する点があります。また、arrowという名前にも関わらずhead_widthとhead_lengthを指定しないと「矢印」が描画されません。

なお、軸を描きたいという場合はaxhlineおよびaxvlineの方が正しい気もしますがこれらの関数では軸に矢印を付けれなかったので採用しませんでした。

text 

plt.text( 3.9, -0.1, '$x$', alpha=alpha)
plt.text(-0.1,  4.0, '$y$', alpha=alpha)

X軸とY軸のラベルを書いています。位置の指定は何回か試してみて決定しました。
なお、原点Oが関数外で書いているのはしばらくすると省かれるようになるためです。

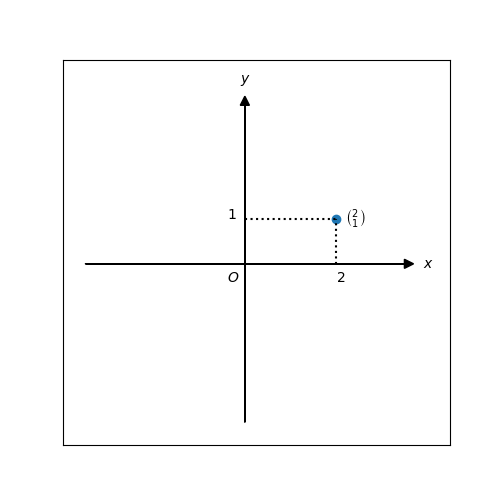
p.138 点のプロット

p.137で点(2, 1)にプロットしていますがそれではおもしろくないので次ページの縦ベクトル表示を行います。

coordinate_plane()
plt.text(-0.4, -0.4, '$O$')

plt.scatter(2, 1)

plt.vlines(2, 0, 1, linestyles='dotted')
plt.hlines(1, 0, 2, linestyles='dotted')

plt.text( 2.0, -0.4, '$2$')
plt.text(-0.4,  1.0, '$1$')

plt.text(2.2, 0.9, r'$\left(\stackrel{2}{1}\right)$')

plt.show()

こんな感じ。

Figure_2.png

ここで難題なのは縦ベクトル表示です。幸いmatplotlibはTeXでの数式表記が使えるのでそれを使えば縦ベクトルも簡単に表示できました。
ところでr''という見慣れない表記がされていますがこう書くとエスケープシーケンスが処理されなくなります。TeXのマクロは\始まりなのでこれを使うとエスケープシーケンスを気にせずにTeXを記述することができます。かくいう私も書いてて初めて知りましたが(笑)2

なお、点(2, 1)からX軸とY軸に下ろしている垂線はarrowでも書けますが今回は意味合い的にvlinesとhlinesを使ってみました。

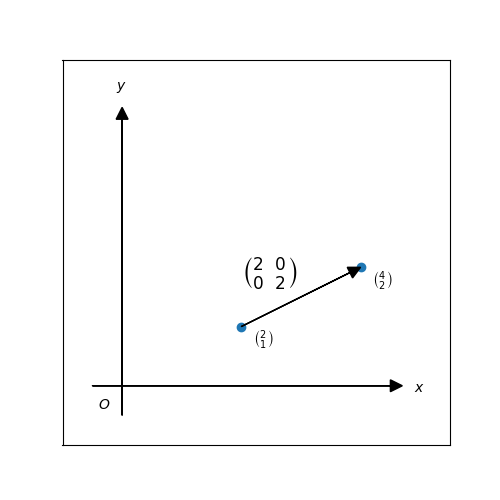
p.141 行列による座標変換と移動の図示

さてやっと行列の登場です。p.141では先ほどの点(2, 1)に行列$\left(\stackrel{2\ \ 0}{0\ \ 2}\right)$を適用し3、点がどう移動したかを矢印で示しています。

まず描画の前に計算を行います。
行列と掛け算するためにはnp.array([[2], [1]])みたいに配列を作る必要があるのですが書きにくいので普通にnp.array([2, 1])で作った後にreshapeします。4

P = np.array([2, 1])
P = P.reshape(-1, 1)

そして行列を作って掛け算します。

A = np.array([[2, 0], [0, 2]])
Q = A @ P

もう少し準備が必要。今回は2点プロットするので変換前、変換後の点のX座標、Y座標をconcatenateを使ってまとめます。

X = np.concatenate((P[0], Q[0]))
Y = np.concatenate((P[1], Q[1]))

それでは描画コードです。この図だけx, yの範囲が異なるのでcoordinate_plane関数に書いたコードをべたに書きます。

plt.figure(figsize=(5, 5))
plt.xticks([])
plt.yticks([])
plt.xlim(-1.0, 5.5)
plt.ylim(-1.0, 5.5)
plt.arrow(-0.5,    0, 5, 0, head_width=0.2, head_length=0.2, color='black')
plt.arrow(   0, -0.5, 0, 5, head_width=0.2, head_length=0.2, color='black')
plt.text( 4.9, -0.1, '$x$')
plt.text(-0.1,  5.0, '$y$')
plt.text(-0.4, -0.4, '$O$')

plt.scatter(X, Y)

for x, y, dx, dy in np.concatenate((P.T, (Q - P).T), axis=1):
    plt.arrow(x, y, dx, dy, head_width=0.2, head_length=0.2, length_includes_head=True, color='black')

plt.text(2.2, 0.7, r'$\left(\stackrel{2}{1}\right)$')
plt.text(4.2, 1.7, r'$\left(\stackrel{4}{2}\right)$')
plt.text(2.0, 1.8, r'$\left(\stackrel{2\ \ 0}{0\ \ 2}\right)$', fontsize='xx-large')

plt.show()

表示結果。

Figure_3.png

差分の計算

描画コード中盤にあるこのコード

for x, y, dx, dy in np.concatenate((P.T, (Q - P).T), axis=1):
    plt.arrow(x, y, dx, dy, head_width=0.2, head_length=0.2, length_includes_head=True, color='black')

これは先ほど説明したようにarrow関数が点Pと点Q指定するのではなく、点Pから点Qへの差分を指定するために書いているコードになります。np.concatenate((P.T, (Q - P).T), axis=1)の結果はarray([[2, 1, 2, 1]])になり、各要素がx, y, dx, dyに代入されるという仕掛けになっています。今回は矢印一本だけなのでここまでする必要はありませんが5、後々のために先行して使い回しのきくコードを作っておきました。

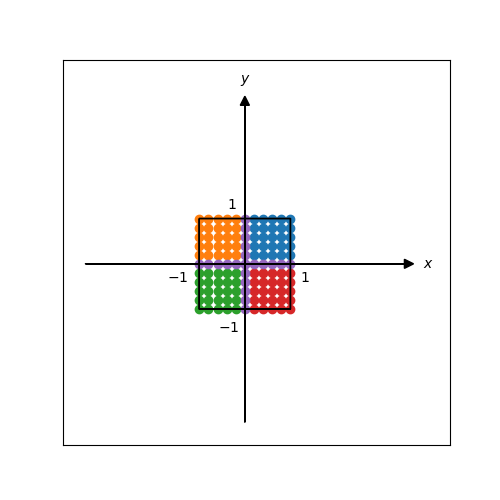
p.145 象限ごとに分けて表示

ページを進めてp.145。今度は複数の点を変換しようということで、その準備として各象限と軸上で点の表示を変えようとミルカさんがリサに要請します。
この無茶ぶりへの対応はmeshgridを使えば可能です。

ap = np.linspace( 0.2,  1.0, 5)
am = np.linspace(-1.0, -0.2, 5)

x1, y1 = np.meshgrid(ap, ap)
x2, y2 = np.meshgrid(am, ap)
x3, y3 = np.meshgrid(am, am)
x4, y4 = np.meshgrid(ap, am)

X軸とY軸上の点は単純にmeshgridではできないので少し工夫が必要です。

X = np.meshgrid(np.linspace(-1.0, 1.0, 11), [0])
Y = np.meshgrid([0], np.linspace(-1.0, 1.0, 11))
x0, y0 = np.concatenate((X[0], Y[0].reshape(1, -11)), axis=1), np.concatenate((X[1], Y[1].reshape(1, -11)))

x0, y0には以下のように配列が設定されます。

>>> x0
array([[-1. , -0.8, -0.6, -0.4, -0.2,  0. ,  0.2,  0.4,  0.6,  0.8,  1. ,
         0. ,  0. ,  0. ,  0. ,  0. ,  0. ,  0. ,  0. ,  0. ,  0. ,  0. ]])
>>> y0
array([[ 0. ,  0. ,  0. ,  0. ,  0. ,  0. ,  0. ,  0. ,  0. ,  0. ,  0. ],
       [-1. , -0.8, -0.6, -0.4, -0.2,  0. ,  0.2,  0.4,  0.6,  0.8,  1. ]])

点が用意できたので後は描画するだけ。

coordinate_plane()

plt.scatter(x1, y1)
plt.scatter(x2, y2)
plt.scatter(x3, y3)
plt.scatter(x4, y4)
plt.scatter(x0, y0)

plt.text( 1.2, -0.4, '$1$')
plt.text(-0.4,  1.2, '$1$')
plt.text(-1.7, -0.4, '$-1$')
plt.text(-0.6, -1.5, '$-1$')

plt.arrow( 1,  1, -2,  0)
plt.arrow(-1,  1,  0, -2)
plt.arrow(-1, -1,  2,  0)
plt.arrow( 1, -1,  0,  2)

plt.show()

表示結果。

Figure_4.png

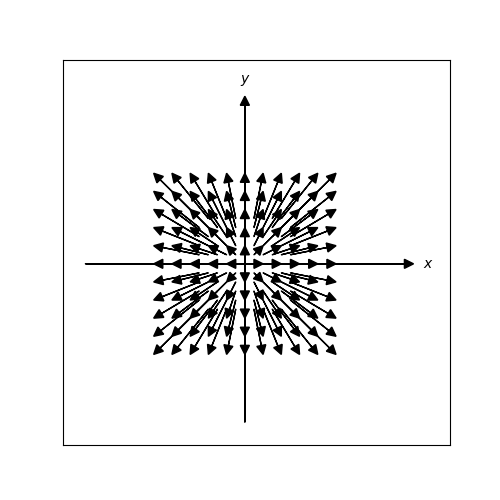
p.147 多点の移動状況を図示

象限ごとの表示ができたところですが、それは一旦置いといてp.147の点移動状況の表示に取り組みます。なおこの図がこの記事を書こうと（matplotlibで再現してみようと）思った発端です。

meshgridは格子点を作成するのに便利なのですがX座標とY座標が分かれて返されるため行列に適用するためには逆にまとめる必要があります。stackを使うことでまとめることができます。

x, y = np.meshgrid(np.linspace(-1.0, 1.0, 11), np.linspace(-1.0, 1.0, 11))
P = np.stack((x.reshape(-1), y.reshape(-1)), axis=-1)

さらに転置して縦ベクトルにしたうえで行列計算！NumPyって便利ですね。

P = P.T
Q = A @ P

では描画します。ここで先ほど作っておいた差分計算コードが役に立ちます（dxとdyがともに0だとエラーになるようなので条件分岐を増やしています）

coordinate_plane()

for x, y, dx, dy in np.concatenate((P.T, (Q - P).T), axis=1):
    if not (dx == 0 and dy == 0):
        plt.arrow(x, y, dx, dy, head_width=0.2, head_length=0.2, length_includes_head=True, color='black')

plt.show()

変換により拡大されていることがよくわかります。テトラちゃんと同様に私も感動しました。

Figure_5.png

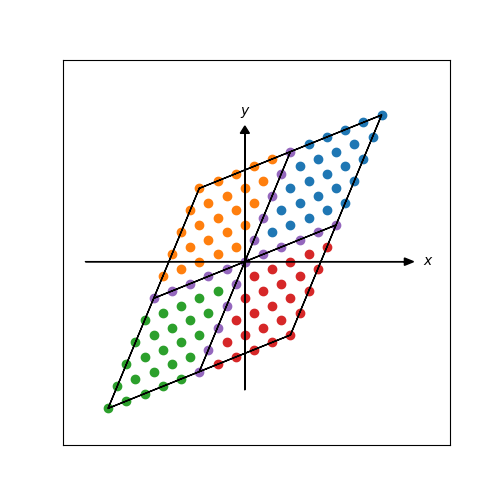
p.156 平行四辺形への変換

幾分ページを進めてp.156。ここでは行列$\left(\stackrel{2\ \ 1}{1\ \ 3}\right)$を使った座標変換が行われています。これを再現してみます。
点を変換してscatterに渡すために補助関数のtransformを定義します。格子点の外接四角形と軸も変換しているのが地味にめんどい。

coordinate_plane()
plt.ylim(-5.0, 5.5)

def transform(x, y, A):
    P = np.stack((x.reshape(-1), y.reshape(-1)), axis=-1)
    P = P.T
    Q = A @ P
    return Q[0], Q[1]

A = np.array([[2, 1], [1, 3]])

plt.scatter(*transform(x1, y1, A))
plt.scatter(*transform(x2, y2, A))
plt.scatter(*transform(x3, y3, A))
plt.scatter(*transform(x4, y4, A))
plt.scatter(*transform(x0, y0, A))

# 外接四角形
c = np.array([[-1, -1], [1, -1], [1, 1], [-1, 1], [-1, -1]])
c = c.T
c2 = A @ c
c2 = c2.T
for i in range(0, 4):
    plt.arrow(c2[i][0], c2[i][1], c2[i+1][0] - c2[i][0], c2[i+1][1] - c2[i][1])

# 軸
a = np.array([[-1, 0], [1, 0], [0, -1], [0, 1]])
a = a.T
a2 = A @ a
a2 = a2.T
for i in range(0, 4, 2):
    plt.arrow(a2[i][0], a2[i][1], a2[i+1][0] - a2[i][0], a2[i+1][1] - a2[i][1])

plt.show()

結果。苦労しただけにドヤ顔はできると思います(笑)

Figure_6.png

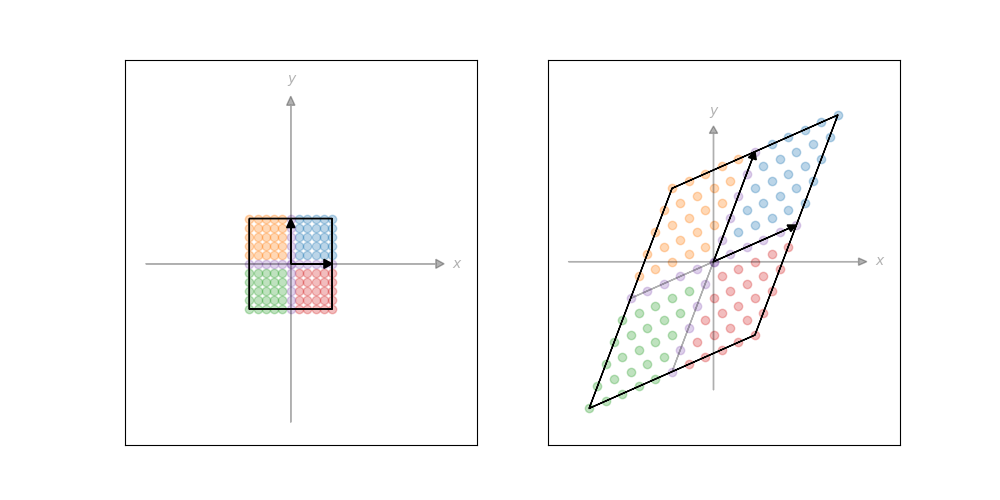
p.159 変換前後の分離表示

p.159では行列による変換がわかるようにと変換前の図、変換後の図を分けて表示しています。
はい、subplotの出番ですね。
・・・とやろうとしたのですが、今回は明示的にFigureを作成しているので単純にplt.subplotした後、coordinate_planeを呼び出すと別のFigureができてしまいます。このあたり、Figureとsubplotの関係を理解していなかったので勉強になりました。

というわけでそれをふまえての描画コード。2つ図を描いているので長いですがやっていることは今までに出てきたことの繰り返しです。
あ、ここでようやくcoordinate_planeに仕込んだ2つの引数が有効活用されます。

alpha=0.3

# 2つの図を描くFigureを用意
fig = plt.figure(figsize=(10, 5))

# 1つ目の図
fig.add_subplot(1, 2, 1)
coordinate_plane(new_figure=False, alpha=alpha)

plt.scatter(x1, y1, alpha=alpha)
plt.scatter(x2, y2, alpha=alpha)
plt.scatter(x3, y3, alpha=alpha)
plt.scatter(x4, y4, alpha=alpha)
plt.scatter(x0, y0, alpha=alpha)

plt.arrow( 1,  1, -2,  0)
plt.arrow(-1,  1,  0, -2)
plt.arrow(-1, -1,  2,  0)
plt.arrow( 1, -1,  0,  2)

plt.arrow(0, 0, 1, 0, head_width=0.2, head_length=0.2, length_includes_head=True, color='black')
plt.arrow(0, 0, 0, 1, head_width=0.2, head_length=0.2, length_includes_head=True, color='black')

# 2つ目の図
fig.add_subplot(1, 2, 2)
coordinate_plane(new_figure=False, alpha=alpha)

plt.ylim(-5.0, 5.5)

plt.scatter(*transform(x1, y1, A), alpha=alpha)
plt.scatter(*transform(x2, y2, A), alpha=alpha)
plt.scatter(*transform(x3, y3, A), alpha=alpha)
plt.scatter(*transform(x4, y4, A), alpha=alpha)
plt.scatter(*transform(x0, y0, A), alpha=alpha)

for i in range(0, 4):
    plt.arrow(c2[i][0], c2[i][1], c2[i+1][0] - c2[i][0], c2[i+1][1] - c2[i][1])

for i in range(0, 4, 2):
    plt.arrow(a2[i][0], a2[i][1], a2[i+1][0] - a2[i][0], a2[i+1][1] - a2[i][1], alpha=alpha)

plt.arrow(0, 0, 2, 1, head_width=0.2, head_length=0.2, length_includes_head=True, color='black')
plt.arrow(0, 0, 1, 3, head_width=0.2, head_length=0.2, length_includes_head=True, color='black')

plt.show()

表示結果。

Figure_7.png

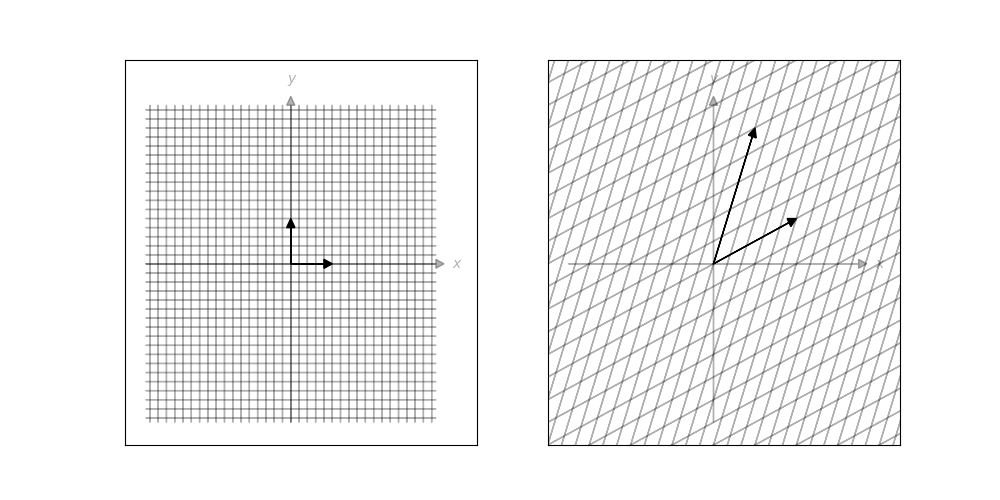
p.160 格子の変換

ページをめくってp.160では座標平面全体が変換される様子を見てみようということが行われています。
これも今までの知見を踏まえると簡単に再現できます。

fig = plt.figure(figsize=(10, 5))

# 1つ目の図
fig.add_subplot(1, 2, 1)
coordinate_plane(new_figure=False, alpha=alpha)

for a in np.linspace(-3.4, 3.4, 35):
    plt.arrow(-3.5,    a, 7, 0, alpha=alpha)
    plt.arrow(   a, -3.5, 0, 7, alpha=alpha)

plt.arrow(0, 0, 1, 0, head_width=0.2, head_length=0.2, length_includes_head=True, color='black')
plt.arrow(0, 0, 0, 1, head_width=0.2, head_length=0.2, length_includes_head=True, color='black')

# 2つ目の図
fig.add_subplot(1, 2, 2)
coordinate_plane(new_figure=False, alpha=alpha)

for a in np.linspace(-3.4, 3.4, 35):
    x = np.array([[-3.5, a], [3.5, a]])
    y = A @ x.T
    plt.arrow(y[0][0], y[1][0], y[0][1] - y[0][0], y[1][1] - y[1][0], alpha=alpha)
    x = np.array([[a, -3.5], [a, 3.5]])
    y = A @ x.T
    plt.arrow(y[0][0], y[1][0], y[0][1] - y[0][0], y[1][1] - y[1][0], alpha=alpha)

plt.arrow(0, 0, 2, 1, head_width=0.2, head_length=0.2, length_includes_head=True, color='black')
plt.arrow(0, 0, 1, 3, head_width=0.2, head_length=0.2, length_includes_head=True, color='black')

plt.show()

実は一つ手抜きがあって、変換後の線の範囲を[-3.5, 3.5]に抑えると再限度が増すのですが、端折っています(笑)

Figure_8.png

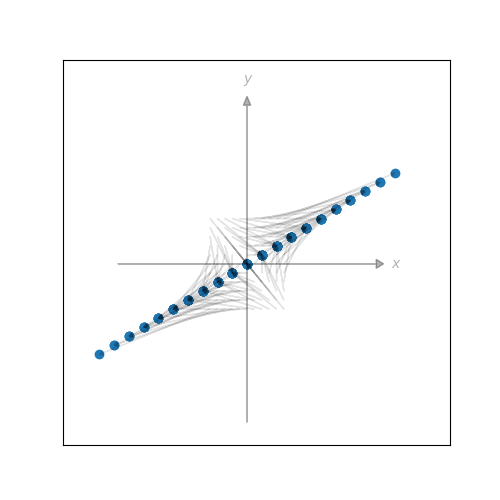
p.203 逆行列がない場合の線形変換

第4章はその後、線型性についての話になり、第5章では変換の合成（行列の積）、逆変換（逆行列）に話が及びます。その中でテトラちゃんが漏らした「逆変換はいつも存在するのに逆行列が存在しないことがあるのは何故か」に対する答えの図が秀逸なので最後の締めとしたいと思います。

A = np.array([[2, 2], [1, 1]])

x, y = np.meshgrid(np.linspace(-1.0, 1.0, 11), np.linspace(-1.0, 1.0, 11))
P = np.stack((x.reshape(-1), y.reshape(-1)), axis=-1)
P = P.T
Q = A @ P

coordinate_plane(alpha=alpha)
plt.xlim(-5.0, 5.5)

for x, y, dx, dy in np.concatenate((P.T, (Q - P).T), axis=1):
    if not (dx == 0 and dy == 0):
        plt.arrow(x, y, dx, dy, head_width=0.1, head_length=0.1, length_includes_head=True, color='black', alpha=0.1)

plt.scatter(Q[0], Q[1])

plt.show()

表示結果。複数の点が一点に収束している様子がよくわかります。

Figure_9.png

おわりに

結論：リサが使っているプログラミング言語はPythonだった！
・・・かは不明です。matplotlibやNumPyについていろいろ知見が得られて楽しかったです。

  1. 2018年11月25日時点 ↩

  2. シングルクォーテーションとダブルクォーテーションに区別がないなんて仕様だからいけないわけで、Rubyのように区別すればいいと思うわけですが。 ↩

  3. Qiitaのインライン数式だと行列がちゃんと表示されないなぁ。 ↩

  4. np.array([2, 1]).Tで縦ベクトルを作ろうとしてもうまくいきません（一次元配列の転置は行えません）。np.array([[2, 1]]).Tなら可能ですがいけてない。 ↩

  5. ただし、縦ベクトルなので添え字を直に書くとかなりわかりにくい。 ↩

9
12
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
9
12