はじめに
スモールデータと機械学習より、主成分分析の理解を深めるために記事を作成します。n番煎じです。
主成分分析をやって何がうれしいの?
- 変数間の共線性がある変数同士をまとめて主成分でデータを表す
- それによりデータセットの次元を減らすことで可視化しやすくする
三角形の「面積」と「周囲長」が相関関係にあれば、その二つの変数をまとめて、「三角形の大きさ」として新しく主成分を作るイメージです。
sklearn のwine_datasetは 3 種類の異なる品種から作られたワインの化学分析結果をまとめたデータセットです。分析項目には灰分濃度やアルコール濃度など、13 種類の特徴量があるため、各品種の特徴を把握することが難しいですが、主成分分析により次元圧縮を行い、特徴量の情報を保存した 2種類の主成分を使用してプロット、ローディングベクトル (各主成分の軸を構成するベクトル) の中身を確認することで、どの特徴量がワインの分類に寄与しているのかについて示唆を得ることができます。
- wine dataset

ローディングベクトルの中身を確認すると、フラボノイド類、総フェノール類が第 1 主成分における正の方向に寄与しており、色の濃さ、アルコール濃度が第 2 主成分における正の方向に寄与していそうです。
導出
第一主成分の導出
$M$個の特徴量を持つデータセット$X (x_1 ... x_n) \in \mathbb{R}^{N \times M}$が存在します。
X
=\begin{pmatrix}
x_{1,1} \cdots x_{1,m} \\
\vdots \qquad \qquad \vdots \\
x_{n,1} \cdots x_{n,m}
\end{pmatrix}
Xに対してオートスケーリングの処理を入れることで、各特徴量の平均を0、分散を1に変換します。ここでは変換前の$X$ の平均を $\mu$ 、分散を $\sigma^{2}$ とします。
$$ (x_n - \mu)/ \sqrt{\sigma^{2}}$$
第一主成分のベクトル(ローディングベクトル)を$ p_1 = (p_{1,1} \cdots p_{m,1})^T \in \mathbb{R}^{M}$とし、そのノルムを $\left|| p \right|| = 1$ とします。$x_n$ を第一主成分のベクトル$p_1$ で射影変換したものを主成分得点$ t_{1,n} $ とすると、主成分得点は以下のように示せます。
\begin{align}
t_{1,n}
&= ||x_n|| \underbrace{\cos{\theta}}_{p_1 とx_n のなす角}\\
&= ||x_n|| \underbrace{\frac{x_n^T p_1}{||x_n||\quad ||p_1||}}_{ベクトルのなす角の公式}\\
&= x_n^T p_1
\end{align}
となります。これを$X$ のすべてのデータ点に適用すると
\begin{pmatrix}
t_{1,1} \\
\vdots \\
t_{1,n}
\end{pmatrix}
=
\begin{pmatrix}
x_{1,1} \cdots x_{1,m} \\
\vdots \qquad \qquad \vdots \\
x_{n,1} \cdots x_{n,m}
\end{pmatrix}
\begin{pmatrix}
p_{1,1} \\
\vdots \\
p_{1,m}
\end{pmatrix}\\
$$t_1 = Xp_1$$
となります。
次に、$t_1$のデータセット内における分散 ${s_{t_1}}^2$ を考えます。
\begin{align}
{s_{t_1}}^2
&= \frac{1}{N-1} \sum_{n=1}^N ({t_{1,n}})^2 \\
&= \frac{1}{N-1} {t_1}^T{t_1} \\
&= \frac{1}{N-1} ({X p_1})^T{X p_1} \\
&= \frac{1}{N-1} p_1^T X^T X p_1 \\
&= \underbrace{p_1^T V p_1}_{V = \frac{1}{N-1} X^T X \in \mathbb{R}^{M \times M}, Xの共分散行列 }
\end{align}
$V$ は $\mathbb{R}^{M \times M}$ の対称行列であるので、その固有値は実数となります。また、分散 $({s_{t_1}}^2)> 0$ であるため、$V$ は半正定値行列となります。
半正定値行列
行列$P$が、実対称行列(要素が実数からなる対称行列)かつ任意の実ベクトル$x$ との内積が $x \cdot Px>0$ を満たす際、$P$ は半正定値行列という。 よく聞く、「主成分分析はデータより分散が最大となる軸を作成する」というステップは、この${s_{t1}}^2$を最大にするローディングベクトルを求めることを意味します。$||p_1|| = 1$であるため、その内積は ${p_1}^T p_1=1$ となります。
そのため、${s_{t_1}}^2 = p_1^T V p_1$ は ${p_1}^T p_1=1$ という制約条件の下で最大化されます。これは等式制約条件のもとにおける最大化なので、ラグランジュの未定乗数法で解くことができます。
目的関数を$J_1$と置くと、
\begin{align}
J_1 = {p_1}^T V p_1 - \lambda({p_1}^T p_1-1)
\end{align}
$J_1$を$p_1$ で偏微分して、0とおくと、
\frac{\partial J_1}{\partial p_1} = 2Vp_1 - 2\lambda p_1 = 0
となります。上の式を変形すると
Vp_1 = \lambda p_1
となるので、固有値問題を解けば、$V$ の固有値が$\lambda$ と求まり、極値をとることになります。
\begin{align}
{s_{t_1}}^2
&= {p_1}^T V p_1 \\
&= {p_1}^T \lambda p_1 \\
&= \lambda {p_1}^T p_1 \\
&= \lambda
\end{align}
そのため、${s_{t_1}}^2 $を最大にする$\lambda$ を求めることで、主成分得点($t_1$)を最大にすることができます。固有値が分かったため、対応する固有ベクトル $p_1$ を求めることで、ローディングベクトルを求めることができます。
\underbrace{(V - \lambda I)p_1}_{Iは単位行列} = 0
第二主成分以降の導出
次に第二主成分以降 $(p_r)$ を求めます。先ほどの固有値問題から、順に大きい $\lambda$ から第 $r$ 主成分のローディングベクトル $p_r$ が導出できそうです。しかし、「$p_r$」と「 $p_r$以外」は直行しなければならないので、${p_r}^T p_i = 0$ $(i = 1 \cdots r-1)$、 ${p_r}^T p_i = 1$ $(i=r)$ の制約の下で以下の条件をラグランジュの未定乗数法に追加します。
J_r = {p_r}^T V p_r - \lambda({p_r}^T p_r-1) -\sum_{i=1}^{r-1} \underbrace{\mu_i}_{{p_r}^T p_i =0 に対するラグランジュの乗数} {p_r}^T p_i
$p_r$ で偏微分すると
\frac{\partial J_r}{\partial p_r} = 2Vp_r - 2\lambda p_r -\sum_{i=1}^{r-1} \mu_i p_i= 0
ローディングベクトル ${p_j}^T$ を左からかけると
2{p_j}^T Vp_r - \underbrace{2\lambda {p_j}^Tp_r}_{= 0} -\underbrace{\sum_{i=1}^{r-1} \mu_i {p_j}^T p_i}_{i=j のときの1 、それ以外で0 のため、\mu_j しか残らない}= 0
{p_j}^T V p_r - \mu_j = 0
{p_j}^T V p_r = {p_j}^T \lambda p_r = 0
であるため、
\mu_j = 0
\begin{align}
\frac{\partial J_r}{\partial p_r}
&= 2Vp_r - 2\lambda p_r -\sum_{i=1}^{r-1} \mu_i p_i \\
&= Vp_r - \lambda p_r \\
&= 0
\end{align}
よって、第一主成分と同様に固有値問題を解くことで第二主成分以降を求めることができます。
コード
sklearn によるPCAの実装結果と比較します。今回は sklearn にある wine dataset を使用します。
# import library
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.datasets import load_wine
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
import matplotlib.cm as cm
# import dataset
data_wine = load_wine()
data = data_wine.data
target = data_wine.target
columns = data_wine.feature_names
target_names = data_wine.target_names
# autoscaling
df_data = pd.DataFrame(data)
df_data_as = (df_data - df_data.mean())/df_data.std()
先ほどの数式の中でデータセットから算出可能な $V$ を計算します。
$$V = \frac{1}{N-1} X^T X$$
# V
V = 1/(df_data_as.shape[0] - 1) * np.cov(df_data_as.T)
$Vp_r = \lambda p_r$ であるため、V の固有値を求めることででローディングベクトル $p_r$ を求めます。
# solving an eigen value problem
eigen_values, eigen_vectors = np.linalg.eig(V)
ローディングベクトル $p_r$ が得られたので、主成分得点 $t$ を求めます。
# principal component score
t = df_data_as @ eigen_vectors
df_pca = pd.DataFrame({"target": target,
"t1": t.iloc[:, 0],
"t2": t.iloc[:, 1]})
sklearn による実装と比較します。主成分の寄与率は各固有値が固有値の総和の中で占める割合から算出します。
# PCA by sklearn
pca_sklearn = PCA()
pca_sklearn.fit(df_data_as)
t_score = pd.DataFrame(pca_sklearn.transform(df_data_as))
# explanation ratio
explanation_ratios_sklearn = pca_sklearn.explained_variance_ratio_
explanation_ratios_numpy = eigen_values/np.sum(eigen_values)
# plot PCA result
fig, ax = plt.subplots(1,2, figsize = (10,6), tight_layout = True)
ax = ax.flatten()
cmap = cm.viridis
colors = cmap([0, 0.5, 1])
ax[0].scatter(t_score.iloc[:, 0], t_score.iloc[:, 1], c = df_pca["target"])
ax[0].set_title("sklearn")
ax[0].set_xlabel(f"PC1 ({round(explanation_ratios_sklearn[0], 3)})")
ax[0].set_ylabel(f"PC2 ({round(explanation_ratios_sklearn[1], 3)})")
ax[1].scatter(df_pca.iloc[:, 1], df_pca.iloc[:,2], c = df_pca["target"])
ax[1].set_title("numpy")
ax[1].set_xlabel(f"PC1 ({round(explanation_ratios_numpy[0], 3)})")
ax[1].set_ylabel(f"PC2 ({round(explanation_ratios_numpy[1], 3)})")
legend_elements = [Line2D([0], [0], marker='o', color='w', markerfacecolor=colors[i], markersize=10, label=target_names[i])
for i in range(len(target_names))]
plt.suptitle('PCA result')
plt.legend(handles=legend_elements, loc='center left', bbox_to_anchor=(1.05, 0.5), fontsize=12)
plt.show()
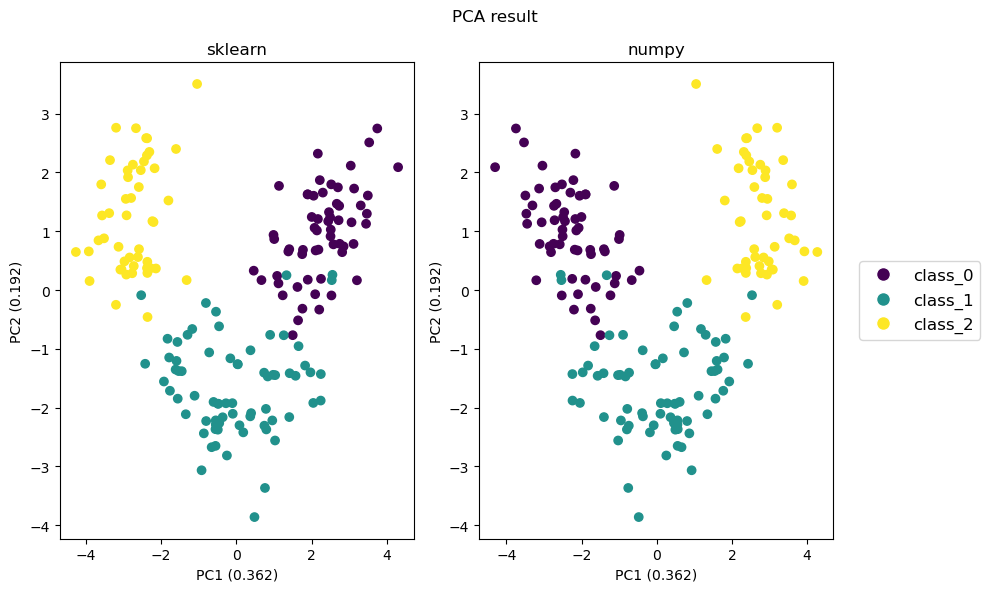
sklearn と numpy で同様なPCAの結果を得ることができました。第 1 主成分の符号が逆になりましたが、第 1 主成分軸の方向は同じであるため、データセットの分散を表現することができます。
おわりに
主成分分析を理解するために、自身の学びを出力しました。違っている点など見つかれば適宜修正します。ご指摘いただけると感謝です。

