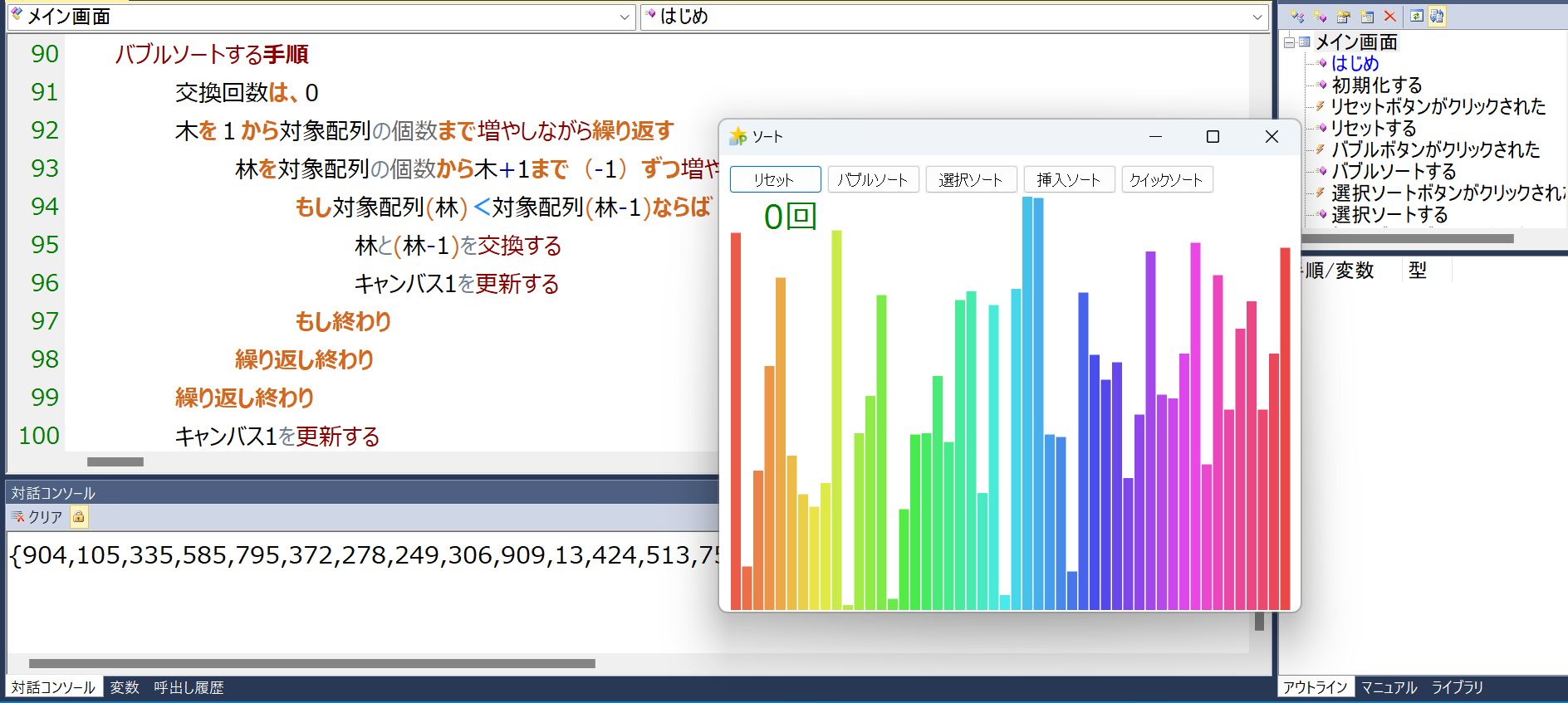
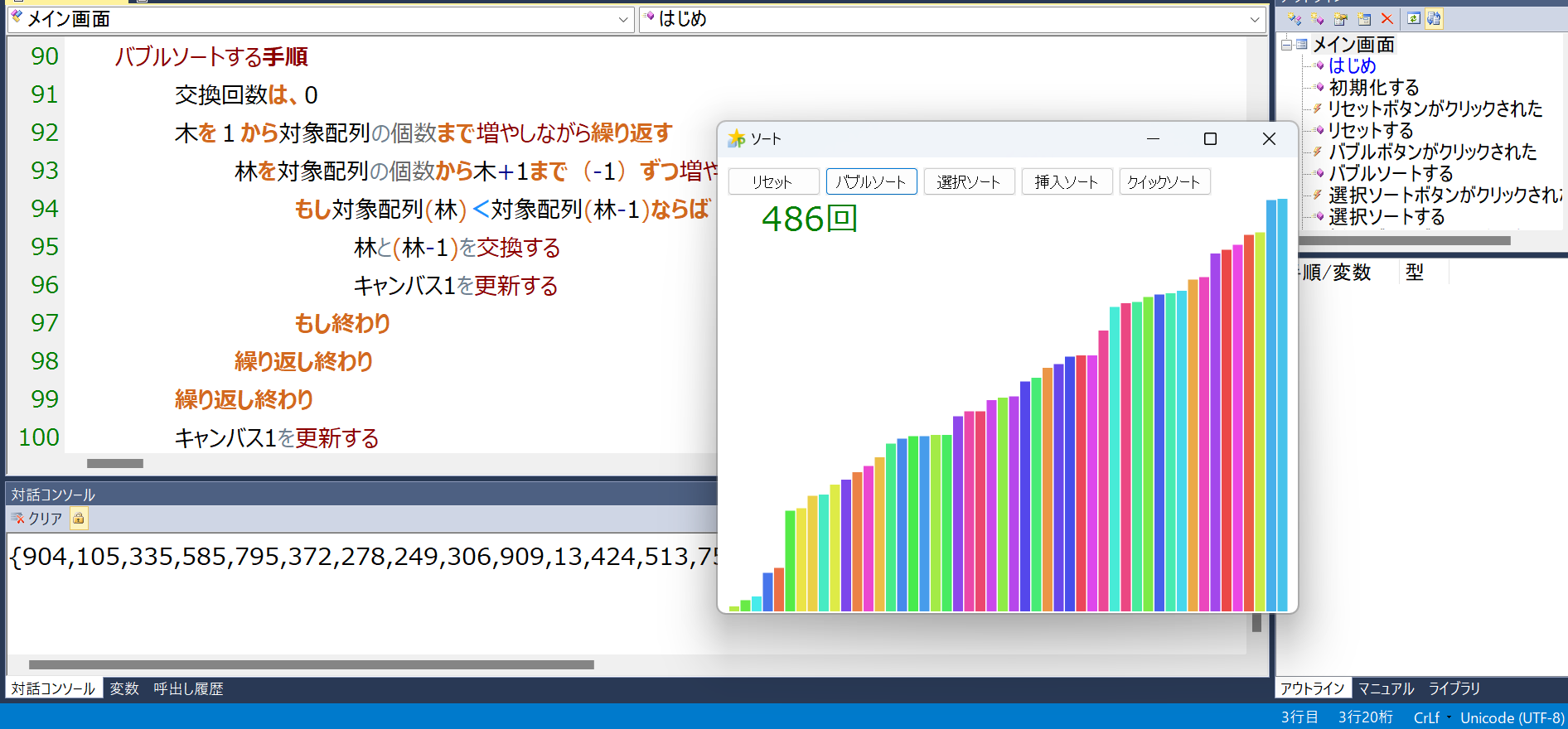
今日は、プロデルでデータを並べ替えるプログラムをいくつかのアルゴリズムで作ってみます。また並べ替えの様子を図で表して、並べ替えられる過程やその回数を見える化してアルゴリズムごとの違いを見比べてみます。
昨年は、プロデルでハノイの塔の答えを可視化してみましたが、今回も同様にキャンバスを用いてアルゴリズムによるデータの変化を可視化してみます。
データの並べ替えそのものは、アルゴリズムを理解しなくても「並べ替える」手順を実行すれば、1行で並べ替えられます。この記事では、日本語プログラミング言語でアルゴリズムを実装した時にどのようなプログラムとなるか紹介できればと思います。
今回は、ソートアルゴリズムのうちで主な4つのアルゴリズムで実装しました。それぞれのアルゴリズムの特徴については割愛させていただきます。詳しい解説は、Qiitaをはじめwikipediaやアルゴリズム関係の書籍にありますのでご参照ください。
- バブルソート
- 選択ソート
- 挿入ソート
- クイックソート
ランダムデータの作成
まずは、並べ替えの対象となるデータを配列で用意します。今回は0から1000までの乱数の整数値を50個生成して配列に入れておきます。
ランダムデータを生成するプログラムは、次の通りです。
最大値は、1000
ソート前は、{}
番号を1から1ずつ増やしながら50まで繰り返す
ソート前(番号)は、0から最大値までの乱数
繰り返し終わり
ソート前を報告する
主要な変数
次のような広域変数を使用します。
- ソート前 (ソート元のランダムデータを格納。50要素)
- 対象配列 (並べ替え対象の配列)
- 総数 (データの個数。50)
- 交換回数 (要素を並べ替えた回数)
- 棒図形配列 (キャンバス上の棒を表す図形。図形の高さが、対象配列での同じ添字の要素の値と対応している)
これらに加えてアルゴリズムごとに変数を定義しています。
アルゴリズムを実装する上での注意
変数のスコープ
プロデルでは、手順の中で明示的に宣言していない変数は、広域変数として自動的に確保されます。局所変数(ローカル変数)として使う変数は、明示的に【 】で宣言する必要があります。再帰が起こる手順を使う場合には、局所変数して宣言しないと、手順が呼び出される度に一つ前に呼び出した時の変数値が維持されず、結果が変わったり無限ループによるスタックオーバースローになることがあるので、注意してください。
配列の添字
プロデルでは、配列の添字が1からはじまりますが、C言語など多くの言語では0から始まります。日本語としては1番目からはじまる方が分かりやすいですが、今回のようなアルゴリズムの実装では混乱することもあるかもしれません。
バブルソート
バブルソートする手順
交換回数は、0
木を1から対象配列の個数まで増やしながら繰り返す
林を対象配列の個数から木+1まで(-1)ずつ増やしながら繰り返す
もし対象配列(林)<対象配列(林-1)ならば
林と(林-1)を要素交換する
キャンバス1を更新する
もし終わり
繰り返し終わり
繰り返し終わり
終わり
選択ソート
選択ソートする手順
交換回数は、0
木を1から増やしながら総数まで繰り返す
最小値は、木
林を木+1から総数まで増やしながら繰り返す
もし対象配列(林)が対象配列(最小値)より小さいなら
最小値は、林
もし終わり
繰り返し終わり
木と最小値を要素交換する
キャンバス1を更新する
繰り返し終わり
終わり
挿入ソート
挿入ソートする手順
交換回数は、0
木を2から対象配列の個数まで増やしながら繰り返す
もし対象配列(木-1)が対象配列(木)より大きいならば
林は、木
【一時】は、対象配列(木)
繰り返す
林と(林-1)を要素交換する
キャンバス1を更新する
林を減らす
もし林が1より大きいかつ対象配列(林-1)が一時より大きいなら繰り返しを続ける
繰り返しから抜け出す
繰り返し終わり
対象配列(林)は、一時
もし終わり
繰り返し終わり
終わり
クイックソート
【開始】から【終了】までクイックソートする手順
もし開始が終了より小さいなら
【中央】は、開始から終了までクイックソート分割する
開始から中央-1までクイックソートする
中央+1から終了までクイックソートする
もし終わり
終わり
【開始番号】から【終了番号】までクイックソート分割する手順
【ピボット】は、開始番号
【左】は、開始番号
【右】は、終了番号+1
左が右より小さい間、繰り返す
繰り返す
左を増やす
もし(対象配列(左)が対象配列(ピボット)より小さい)なら繰り返しを続ける
繰り返しから抜け出す
繰り返し終わり
繰り返す
右を減らす
もし(対象配列(ピボット)が対象配列(右)より小さい)なら繰り返しを続ける
繰り返しから抜け出す
繰り返し終わり
もし左が右より小さいなら
左と右を要素交換する
キャンバス1を更新する
もし終わり
繰り返し終わり
ピボットと右を要素交換する
キャンバス1を更新する
右を返す
終わり
完成したプログラム
動作する完全なプログラムは、次の通りです。
生成したランダムデータの値がキャンバス上に描いたグラフで表示されます。
各アルゴリズムごとにボタンをクリックすると、それぞれのアルゴリズムで棒が並べ替えられます。
動作環境:プロデル1.9.1164
最大値は、1000
ソート前は、{}
番号を1から1ずつ増やしながら50まで繰り返す
ソート前(番号)は、0から最大値までの乱数
繰り返し終わり
ソート前を報告する
総数は、ソート前の個数
棒図形配列は、{}
メイン画面を表示する
待機する
メイン画面とは
ウィンドウを継承する
-交換回数
はじめの手順
初期化する
ーー貼り付けた部品に対する操作をここに書きます
この実質大きさを{700,550}に変える
図余白は、30
リセットする
キャンバス1へ「0回」という文字を描いて"交換回数ラベル"とする
その位置は{30,30}
そのフォントを「メイリオ」に変える
その文字色を緑色に変える
その文字サイズを20に変える
終わり
初期化する手順
ーー自動生成された手順です。ここにプログラムを書き加えても消える場合があります
この実質大きさを{696,394}に変える
この初期位置を「中央」に変える
この内容を「ソート」に変える
初期化開始する
クイックボタンというボタンを作る
その位置と大きさを{484,12,112,34}に変える
その内容を「クイックソート」に変える
その移動順を6に変える
挿入ボタンというボタンを作る
その位置と大きさを{366,12,112,34}に変える
その内容を「挿入ソート」に変える
その移動順を5に変える
選択ソートボタンというボタンを作る
その位置と大きさを{248,12,112,34}に変える
その内容を「選択ソート」に変える
その移動順を4に変える
バブルボタンというボタンを作る
その位置と大きさを{130,12,112,34}に変える
その内容を「バブルソート」に変える
その移動順を3に変える
リセットボタンというボタンを作る
その位置と大きさを{12,12,112,34}に変える
その内容を「リセット」に変える
その移動順を1に変える
キャンバス1というキャンバスを作る
その位置と大きさを{0,0,696,394}に変える
その自動更新を×に変える
その移動順を2に変える
そのドッキング方向を「全体」に変える
初期化終了する
この設計スケール比率を{144,144}に変える
終わり
リセットボタンがクリックされた時の手順
リセットする
終わり
リセットする手順
線幅は、(キャンバス1の紙幅-総数)/(総数+2)
線高さは、キャンバス1の紙高さ-図余白
線高さ倍率は、線高さ/最大値
対象配列は、ソート前のクローン
棒図形配列のすべての棒についてそれぞれ繰り返す
キャンバス1から棒を消す
繰り返し終わり
木を1からソート前の個数まで増やしながら繰り返す
キャンバス1へ四角形を描いて棒とする
その位置と大きさは{木*線幅+木,線高さ-ソート前(木)*線高さ倍率+図余白,線幅,ソート前(木)*線高さ倍率}
その背景色は、HLS({(木*360/総数)%360,0.8,0.6})
その太さは、0
棒図形配列(木)=棒
繰り返し終わり
キャンバス1を更新する
終わり
バブルボタンがクリックされた時の手順
バブルソートする
終わり
バブルソートする手順
交換回数は、0
木を1から対象配列の個数まで増やしながら繰り返す
林を対象配列の個数から木+1まで(-1)ずつ増やしながら繰り返す
もし対象配列(林)<対象配列(林-1)ならば
林と(林-1)を要素交換する
キャンバス1を更新する
もし終わり
繰り返し終わり
繰り返し終わり
キャンバス1を更新する
終わり
選択ソートボタンがクリックされた時の手順
選択ソートする
終わり
選択ソートする手順
交換回数は、0
木を1から増やしながら総数まで繰り返す
最小値は、木
林を木+1から総数まで増やしながら繰り返す
もし対象配列(林)が対象配列(最小値)より小さいなら
最小値は、林
もし終わり
繰り返し終わり
木と最小値を要素交換する
キャンバス1を更新する
繰り返し終わり
キャンバス1を更新する
終わり
挿入ボタンがクリックされた時の手順
挿入ソートする
終わり
挿入ソートする手順
交換回数は、0
木を2から対象配列の個数まで増やしながら繰り返す
もし対象配列(木-1)が対象配列(木)より大きいならば
林は、木
【一時】は、対象配列(木)
繰り返す
林と(林-1)を要素交換する
キャンバス1を更新する
林を減らす
もし林が1より大きいかつ対象配列(林-1)が一時より大きいなら繰り返しを続ける
繰り返しから抜け出す
繰り返し終わり
対象配列(林)は、一時
もし終わり
繰り返し終わり
キャンバス1を更新する
終わり
クイックボタンがクリックされた時の手順
交換回数は、0
1から対象配列の個数までクイックソートする
キャンバス1を更新する
終わり
【開始】から【終了】までクイックソートする手順
もし開始が終了より小さいなら
【中央】は、開始から終了までクイックソート分割する
開始から中央-1までクイックソートする
中央+1から終了までクイックソートする
もし終わり
終わり
【開始番号】から【終了番号】までクイックソート分割する手順
【ピボット】は、開始番号
【左】は、開始番号
【右】は、終了番号+1
左が右より小さい間、繰り返す
繰り返す
左を増やす
もし(対象配列(左)が対象配列(ピボット)より小さい)なら繰り返しを続ける
繰り返しから抜け出す
繰り返し終わり
繰り返す
右を減らす
もし(対象配列(ピボット)が対象配列(右)より小さい)なら繰り返しを続ける
繰り返しから抜け出す
繰り返し終わり
もし左が右より小さいなら
左と右を要素交換する
キャンバス1を更新する
もし終わり
繰り返し終わり
ピボットと右を要素交換する
キャンバス1を更新する
右を返す
終わり
【A】と【B】を要素交換する手順
対象配列からA番目とB番目を交換する
棒図形配列からA番目とB番目を交換する
棒図形配列(A)の横は、A*線幅+A
棒図形配列(B)の横は、B*線幅+B
交換回数を増やす
交換回数ラベルの内容は「[交換回数]回」
終わり
終わり
実行画面
まとめ
今回はプロデルでアルゴリズムを実装してみました。競技プログラミングとしてプロデルが採用されている実績もありますので、ユニークな言語のひとつとしてプロデルで問題を解くのも面白いかと思います。
ソート以外にも著名なアルゴリズムはたくさんあります。C#言語やPythonなどほかの言語での実装プログラムが豊富に公開されていますので、プロデルで実装して理解を深めることも楽しいと思います。
関連記事