概要
講談社MLPの「異常検知と変化検知」を読んで、何か具体的な問題で試してみたいと思ったので、「方向データの異常検知」を文章の埋め込みベクトルに適用して、文章群に混じった異質な文章を検知できるか試してみました。具体的には、夏目漱石の小説から取った文章群の中に企業の有価証券報告書から取った文章を少数だけ混ぜて、異質なデータである有価証券報告書の文章を検知する機械学習モデルを作成しました。埋め込みベクトル(分散表現)の計算にはMultilingual Universal Sentence Encoderを用いています。
方向データの異常検知
「異常検知と変化検知」(著:井出剛、杉山将)のChapter 7「方向データの異常検知」から必要な事項をまとめます。
正解ラベルの付いていないデータ $\mathcal{D}$ を用いて異常検知モデルを作成するときの基本的な考え方は、データに含まれる異常標本の数が非常に少ないと仮定して、正常データの分布 $p(x|\mathcal{D})$ を推定し、分布から外れている標本を異常とみなすというものです。具体的には異常度を$$a(x^\prime) = - \ln p(x^\prime|\mathcal{D}) \tag{1}$$で定義して、異常度が閾値を超えた時に$x^\prime$を異常と判定します。
データ $\mathcal{D}=\{\boldsymbol{x}^{(n)}|n=1,\cdots,N\}$ が単位ベクトル$\boldsymbol{x}^{(n)}$からなる方向データである場合は、データ分布としてフォンミーゼス・フィッシャー分布 (von Mises-Fisher distribution) $$\mathcal{M} (\boldsymbol{x} |\boldsymbol{\mu}, \kappa) = \frac{\kappa^{M/2-1}}{(2\pi)^{M/2} I_{M/2-1}(\kappa)} \exp(\kappa \boldsymbol{\mu}^\top \boldsymbol{x}) \tag{2}$$を考えるのが自然です。分布は2つのパラメータ、平均方向$\boldsymbol{\mu}$と集中度$\kappa$を持ちます。平均方向$\boldsymbol{\mu}$も単位ベクトルです。ここで$M$はベクトル$\boldsymbol{x}$の次元、$I_{M/2-1}(\kappa)$は第1種変形ベッセル関数です。分布の係数部分は正規化条件$$\int_{S_M}\! d\boldsymbol{x}, \mathcal{M} (\boldsymbol{x} |\boldsymbol{\mu}, \kappa) = 1$$から決まっています。ここで、$S_M$は積分範囲が$M$次元空間の単位球表面であることを表しています。
異常検知モデル作成の流れは非常に単純で、大まかには以下の通りです。
1.与えられたデータ $\mathcal{D}$ を用いて最尤推定などによりパラメータ$\boldsymbol{\mu}$と$\kappa$を決定する。
2.$\mathcal{D}$ に含まれない新たなデータ$\boldsymbol{x}^\prime$に対して異常度$a(\boldsymbol{x}^\prime)$を計算し、閾値を超えるかどうかで異常かどうかを判定。
まず、$\boldsymbol{\mu}$を決定する最尤推定をします。条件$\boldsymbol{\mu}^\top \boldsymbol{\mu}=1$をラグランジュ係数$\lambda$を用いて取り込むと$$0=\frac{\partial}{\partial \boldsymbol{\mu}} \left\{ \ln \prod_{n=1}^N \mathcal{M} (\boldsymbol{x}^{(n)} |\boldsymbol{\mu}, \kappa) -\lambda \boldsymbol{\mu}^\top \boldsymbol{\mu} \right\}=\kappa \sum_{n=1}^N \boldsymbol{x}^{(n)} -2\lambda \boldsymbol{\mu}$$が得られます。条件$\boldsymbol{\mu}^\top \boldsymbol{\mu}=1$を使って係数$\lambda$を消去すれば、$\boldsymbol{\mu}$をデータ $\mathcal{D}$ から決定する式$$\hat{\boldsymbol{\mu}}=\frac{\boldsymbol{m}}{\sqrt{\boldsymbol{m}^\top \boldsymbol{m}}} \hspace{10pt} \text{where} \hspace{10pt} \boldsymbol{m}=\frac{1}{N}\sum_{n=1}^N \boldsymbol{x}^{(n)} \tag{3}$$が得られます。これはデータベクトルの平均方向が分布の中心に一致するという結果で直感的にも納得のいくものでしょう。
次に$\kappa$を決定したいのですが、分布(2)はベッセル関数を通じて複雑に$\kappa$に依存しているので、最尤推定をしても方程式を解析的に解くことはできません。そこで、モーメント法を用いて$\kappa$を推定します。ここでいうモーメント法とは、仮定した分布から何らかの量のモーメント(期待値や2乗期待値など)を計算し、それらをデータ標本から計算したモーメントと等値することで、仮定した分布のパラメータを決定する方法です。ここでは、異常度に対してモーメント法を適用します。まず、フォンミーゼス・フィッシャー分布(2)を異常度(1)に代入すると $a(\boldsymbol{x}^\prime) = \text{const} -\kappa \hat{\boldsymbol{\mu}}^\top \boldsymbol{x}^\prime$ が得られます。constは$\boldsymbol{x}^\prime$に依存しない定数です。さらに、異常度に定数をかけたり足したりする操作は閾値の再定義で吸収できる事実を使って、$$a(\boldsymbol{x}^\prime) = 1 -\hat{\boldsymbol{\mu}}^\top \boldsymbol{x}^\prime \tag{4}$$とすることができます。単位ベクトルどうしの内積の取りうる値の範囲は$[-1,1]$ですので、異常度の取りうる値の範囲は$0\leq a\leq 2$です。$\boldsymbol{x}$がフォンミーゼス・フィッシャー分布(2)に従うとき、異常度$a$の確率分布は$$p(a)=\int_{S_M}\! d\boldsymbol{x}, \delta\left(a-(1 -\hat{\boldsymbol{\mu}}^\top \boldsymbol{x})\right) \mathcal{M} (\boldsymbol{x} |\hat{\boldsymbol{\mu}}, \kappa) $$と書き下せます。デルタ関数を用いて積分を実行し、データ点の平均方向$\hat{\boldsymbol{\mu}}$周りのばらつきは小さい、すなわち$a\ll 1$であると仮定すると、近似的に$$p(a) \simeq c, a^{(M-1)/2-1}\exp(-\kappa a)$$が得られます。$c$は$a$に依らない定数です。この分布はカイ2乗分布$$\chi^2 (x|m,s)=\frac{1}{2s\Gamma(m/2)}\left(\frac{x}{2s}\right)^{m/2-1}\exp\left(-\frac{x}{2s}\right) \tag{5}$$で$m=M-1$, $s=1/(2\kappa)$としたものに一致します。異常度$a$の従う分布がわかりましたので、1次と2次のモーメントを以下のように計算することができます1。$$\langle a\rangle=\int_0^\infty \! da, a, \chi^2(a|m,s)=ms$$ $$\langle a^2\rangle=\int_0^\infty \! da, a^2, \chi^2(a|m,s)=m(m+2)s^2 .$$一方で、モーメントはデータ標本$\boldsymbol{x}^{(n)}$から$$\langle a\rangle \simeq \frac{1}{N}\sum_{n=1}^N a(\boldsymbol{x}^{(n)}) \ , \hspace{10pt} \langle a^2\rangle \simeq \frac{1}{N}\sum_{n=1}^N a(\boldsymbol{x}^{(n)})^2$$と評価することもできます。2つの表現を等値することで、パラメータの推定値$$\hat{m}=\frac{2\langle a\rangle^2}{\langle a^2\rangle -\langle a\rangle^2} \ , \hspace{10pt} \hat{s} =\frac{\langle a^2\rangle -\langle a\rangle^2}{2\langle a\rangle} \tag{6}$$が得られます。こうして得られた$\hat{m}$は理想的には$M-1$($M$はベクトルの次元)に等しいはずですが、後で示すように実際は$M$よりかなり小さくなります。これはデータの主要なばらつきが一部の変数に集中しているからで、その意味で$\hat{m}$は有効次元と呼ばれます。はじめの目的だった$\kappa$の推定値は関係式$\hat{\kappa}=1/(2\hat{s})$から求められますが、異常度を(4)式のように$\kappa$を含まない形で再定義しているので、実は$\hat{\kappa}$の値を直接使う必要はもはやありません。異常度の閾値を決めるプロセスで$\hat{m}$と$\hat{s}$を用いるので、そこで間接的に$\hat{\kappa}$の値を使ったことになります。
さて、異常度$a$の従う分布が$\chi^2 (a|\hat{m}, \hat{s})$と推定できましたので、新たなデータ$\boldsymbol{x}^\prime$に対して異常度を式(4)を用いて計算し、その値が分布から外れていれば異常データであると判定できます。判定基準としては、誤報率$\alpha$を何らかの経験則により決めて、$$1-\alpha = \int_0^{a_\text{th}} \! dx, \chi^2 (x|\hat{m}, \hat{s}) \tag{7}$$を解くことで、異常度の閾値$a_\text{th}$を求めることができます2。上の式から明らかなように、誤報率$\alpha$は確率分布の端の何パーセントに入ったら異常データという基準を与えるものです。以下で示す実装では、ニュートン法を用いてこの式を解いています。
Universal Sentence Encoder
Universal Sentence Encoder (USE)は任意の長さの文章を512次元のベクトルに変換するエンコーダーモデルです。自然言語処理の様々なタスクで事前学習されています。BERTなどの汎用言語モデルと違って、正解ラベル付きの教師あり学習により事前学習されているので、事前学習と同種のタスクに対してはファインチューニングなしでも高い性能を発揮します。特に、文章の類似度を判定するタスクはコサイン類似度をターゲットに学習されているので、コサイン類似度を使ったタスクと相性が良いです。今回の異常検知モデルはベクトルの内積から異常度を計算しますので、USEに向いたタスクであると期待できます。
2018年にGoogleが発表した最初のバージョンは英語の文章にのみ対応していましたが、2019年に発表されたMultilingual USEは日本語を含む16言語に対応しています。モデルが16種類あるわけではなく、単一のモデルが16言語に対応しています。多言語バージョンは同一言語内での学習タスクと異言語間での翻訳タスクで事前学習されています。英語以外の学習データを水増しするために、なんと英語のデータセットをGoogle翻訳したそうです。
モデルのアーキテクチャは(論文にもあまり詳細が書かれていないのですが)英語バージョンはTransformerを用いたものと、Deep Averaging Network (DAN)を用いたものがあります。DANの方は精度は落ちるものの軽量なモデルとなっています。多言語バージョンもアーキテクチャは2種類あるのですが、軽量モデルはDANではなくCNNとなっています。TransformerでもCNNでもトークンレベルの埋め込みベクトルを平均したものを文章の埋め込みベクトルとしているようです。文章のトークン化にはSentencePieceが使われており、日本語を入力する場合にも事前に分かち書きをする必要はありません。
いずれのバージョンの学習済みモデルもTensorFlow Hubから使用でき、多言語・Transformer版はUSE-multilingual-large、多言語・CNN版はUSE-multilingualからアクセスできます。今回の実験では軽量なCNN版を使用します3。また、USEモジュールの出力は初めから単位ベクトルに正規化されています。
実装
環境
Ubuntu 18.04.4 LTS (docker on windows)
Python 3.7.6
tensorflow 2.1.0
tensorflow-hub 0.8.0
tensorflow-text 2.1.1
(2021/6/21追記)
Githubにコードを上げました。(各ライブラリのバージョンは上記とは異なっています。)
https://github.com/jovyan70/sentence-anomaly-detection
データ準備
夏目漱石の小説の文章は後期3部作「彼岸過迄」「行人」「こころ」を使用することとします。青空文庫からBeautifulSoupを用いてスクレイピングします。以下のサイトを参考にしました。
import json
import requests
from bs4 import BeautifulSoup
import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path
import random
from sklearn.model_selection import train_test_split
url_list = ['https://www.aozora.gr.jp/cards/000148/files/773_14560.html', # 彼岸過迄
'https://www.aozora.gr.jp/cards/000148/files/765_14961.html', # 行人
'https://www.aozora.gr.jp/cards/000148/files/775_14942.html', # こころ
]
def fetch_sentences(aozora_url):
res = requests.get(aozora_url)
soup = BeautifulSoup(res.content, 'html.parser', from_encoding='utf-8')
main_text = soup.find("div", class_='main_text')
#ルビが振ってあるのを削除
for yomigana in main_text.find_all(["rp","h4","rt"]):
yomigana.decompose()
sentences = [line.strip() for line in main_text.text.strip().splitlines()]
return sentences
souseki_texts = []
for url in url_list:
souseki_texts += fetch_sentences(url)
print(len(souseki_texts))
# 6102
リストsouseki_textsの要素は、いくつかの文をまとめたパラグラフになっていますので、句点ごとに分割することとします。これは、この後ダウンロードするchABSAデータセットの有価証券報告書の文章と形式を合わせるためです。
def split_texts(texts_input):
texts_output = []
for t in texts_input:
texts_output += t.split('。')
return texts_output
souseki_texts = split_texts(souseki_texts)
print(len(souseki_texts))
# 21011
さらに、短すぎる文章と長すぎる文章を除きます。リストには空白も含まれていますが、この操作で同時に除去されます。
def filter_by_length(texts_input, min_len=20, max_len=300):
texts_output = []
for s in texts_input:
length = len(s)
if length >= min_len and length <= max_len:
texts_output.append(s)
return texts_output
souseki_texts = filter_by_length(souseki_texts)
print(len(souseki_texts))
# 12221
文章の前処理(正規化)は特に行いません。
次に、chABSA-datasetをダウンロードして有価証券報告書の文章を採取します。chABSA-datasetは上場企業の有価証券報告書をベースに作成されたデータセットで、各文章の部分部分にネガティブ・ポジティブのラベルがついたものです。詳しい使用例については
が参考になります。今回はラベルは使用せず有価証券報告書の文章のみを使います。
!wget https://s3-ap-northeast-1.amazonaws.com/dev.tech-sketch.jp/chakki/public/chABSA-dataset.zip && \
unzip chABSA-dataset.zip
data_path = Path("chABSA-dataset")
path_list = [p for p in data_path.glob("*.json")]
chabsa_texts = []
for p in path_list:
with open(p, "br") as f:
j = json.load(f)
for line in j["sentences"]:
chabsa_texts += [line["sentence"].replace('\n', '')]
print(len(chabsa_texts))
# 6119
漱石の文章と同様に、短すぎる文章と長すぎる文章を除きます。
chabsa_texts = filter_by_length(chabsa_texts)
print(len(chabsa_texts))
# 5148
これで2種類の文章群の準備ができましたので、2つを混ぜてデータセットを作ります。まず、漱石にラベル0、有価証券報告書にラベル1を付与します。
souseki_length = len(souseki_texts)
souseki_arr = np.hstack([np.reshape(np.zeros(souseki_length), (-1, 1)), np.reshape(souseki_texts, (-1, 1))])
chabsa_length = len(chabsa_texts)
chabsa_arr = np.hstack([np.reshape(np.ones(chabsa_length), (-1, 1)), np.reshape(chabsa_texts, (-1, 1))])
データセットはモデル開発用(dev)とテスト用(test)の2つ用意します。漱石の文章の8割を開発用に、残り2割をテスト用に使います。開発データには漱石の文章の1%の量だけ有価証券報告書の文章を混ぜます。テスト用に関しては、精度評価をしやすいように漱石の文章と有価証券報告書の文章は同数とします。
num_s_dev = int(souseki_length * 0.8)
num_c_dev = int(num_s_dev * 0.01)
num_s_test = souseki_length - num_s_dev
num_c_test = num_s_test
print("開発データ 漱石:{}, 有報:{}".format(num_s_dev, num_c_dev))
print("テストデータ 漱石:{}, 有報:{}".format(num_s_test, num_c_test))
# 開発データ 漱石:9776, 有報:97
# テストデータ 漱石:2445, 有報:2445
s_dev, s_test = train_test_split(souseki_arr, train_size=num_s_dev)
c_dev, c_test = train_test_split(chabsa_arr, train_size=num_c_dev)
c_test, _ = train_test_split(c_test, train_size=num_c_test)
dev_arr = np.vstack([s_dev, c_dev])
np.random.shuffle(dev_arr)
test_arr = np.vstack([s_test, c_test])
np.random.shuffle(test_arr)
print(dev_arr.shape, test_arr.shape)
# (9873, 2) (4890, 2)
テストデータの最初のいくつかをサンプルしてみると、以下のようになります。
1: 可塑剤の出荷数量は増加したものの、原料価格の下落に伴う販売価格の引き下げにより、売上高は46億3百万円となり、前連結会計年度に比べ1億25百万円の減収(同2.7%減)となりました
0: その或ものは水の色を離れない蒼い光を鱗に帯びて、自分の勢で前後左右に作る波を肉の裏に透すように輝やいた
0: 彼はやむを得ず、手紙で用を弁ずる事にした
1: 健康ビジネス部門については、Eウール毛布シリーズが順調に売上を伸ばしたものの、その他の健康寝具関係での対前年の反動減が響き、売上高は前期を下回った
1: また製紙薬剤関連原料は前年度実績を下回りましたものの、炭素製品は堅調に推移し、インキ用原料は前年度並みとなりました
0: 未亡人は私の身元やら学校やら専門やらについて色々質問しました
0: 要するに、勝っても負けても、炬燵にあたって、将碁を差したがる男であった
0: お兼さんだけは依然として元の席を動かなかった
1: 当事業年度の経営成績は次のとおりであります
0: 彼はそう云って、すたすた山の方へ歩いて行ったそうです
人間の目で見ると容易に夏目漱石か有価証券報告書かを判別できそうですね。それでは、異常検知モデルを構築して、モデルが2種類の文章を判別をできるかどうか見ていきましょう。
異常検知モデル開発
まず初めに、Universal Sentence Encoder (USE)を用いて、文章を埋め込みベクトルに変換します。必要なライブラリをインポートし、TensorFlow Hubからモデル(Multilingual, CNN版)をロードします。
import tensorflow_hub as hub
import tensorflow_text
import tensorflow as tf
use_url = 'https://tfhub.dev/google/universal-sentence-encoder-multilingual/3'
embed = hub.load(use_url)
USEモデルの使い方は単純で、ロードした関数embedに文章のリストを与えれば、tf.Tensor形式の埋め込みベクトル(単位ベクトル)のリストを返してくれます。全ての文章を一括で渡すとメモリの使用量が大きくなるので、バッチを分割して計算します。
def get_embeddings(texts, batch_size=100):
length = len(texts)
n_loop = int(length / batch_size) + 1
embeddings = embed(texts[: batch_size])
for i in range(1, n_loop):
arr = embed(texts[batch_size*i: min(batch_size*(i+1), length)])
embeddings = tf.concat([embeddings, arr], axis=0)
return np.array(embeddings)
dev_embeddings = get_embeddings(dev_arr[:, 1])
test_embeddings = get_embeddings(test_arr[:, 1])
print(dev_embeddings.shape, test_embeddings.shape)
# (9873, 512) (4890, 512)
こうして得られた、dev_embeddingsを式(3)に代入して、平均方向の推定値$\hat{\boldsymbol{\mu}}$を求めます。
mu = np.mean(dev_embeddings, axis=0)
mu /= np.linalg.norm(mu)
print(mu.shape)
# (512,)
次に、式(4)により開発データの各標本に対して異常度を計算し、それを式(6)に代入することで、異常度の従うカイ2乗分布のパラメータ$\hat{m}$と$\hat{s}$を推定します。
anom = 1 - np.inner(mu, dev_embeddings)
anom_mean = np.mean(anom)
anom_mse = np.mean(anom**2) - anom_mean**2
mhat = 2 * anom_mean**2 / anom_mse
shat = 0.5 * anom_mse / anom_mean
print("mhat: {:.1f}".format(mhat))
print("shat: {:.3e}".format(shat))
# mhat: 111.7
# shat: 5.406e-03
すでに述べたように、$\hat{m}$は理想的には$M-1$に一致するはずですが、実際の値は111.7で$M-1=511$よりかなり小さくなっています。
求めたパラメータに対して、カイ2乗分布の確率密度関数PDF(5)と累積分布関数CDF(式(7)の右辺)をプロットすると以下のようになります。左図には実際の異常度の分布もヒストグラムでプロットしています。確かにカイ2乗分布でフィット出来ていることが見て取れます。
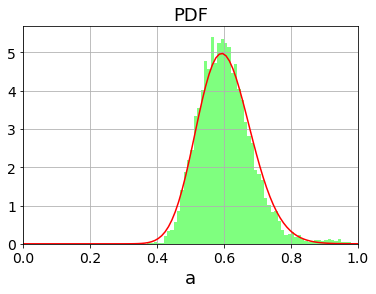
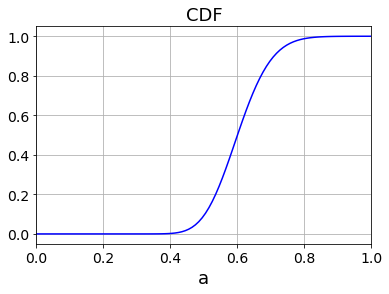
最後に式(7)を解いて閾値$a_\text{th}$を求めれば異常検知モデルが完成します。そのためには誤報率$\alpha$を設定する必要があります。誤報率は何らかのヒューリスティクスによって決める必要がありますが、今回は開発データには異常データが約1%含まれることを知っていますので、$\alpha=0.01$と設定します。式(7)はニュートン法で以下のように解くことができます。
from scipy.stats import chi2
alpha = 0.01
x = 0.8 # initial value
for i in range(100):
xnew = x - (chi2.cdf(x, mhat, loc=0, scale=shat) - (1 - alpha)) / chi2.pdf(x, mhat, loc=0, scale=shat)
if abs(xnew - x) < 1.e-12:
print("iteration: ", i+1)
break
x = xnew
ath = x
print("ath: {:.4f}".format(ath))
# iteration: 5
# ath: 0.8077
精度評価
モデルが完成しましたので、テストデータを使って精度評価を行います。
まず、開発データから評価した平均方向$\hat{\boldsymbol{\mu}}$を使って、テストデータに対する異常度を計算します。
anom_test = 1 - np.inner(mu, test_embeddings)
得られた異常度を閾値と比較して、閾値より大きければ異常標本として判定します。
predict = (anom_test > ath).astype(np.int)
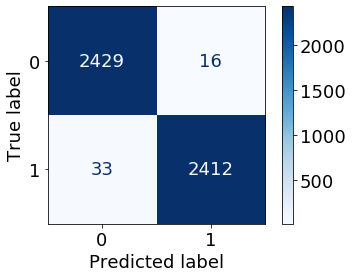
予測値を正解データと比較することで各種精度指標を計算します。混同行列の表示にはConfusionMatrixDisplayを利用しました。
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, confusion_matrix, ConfusionMatrixDisplay
answer = test_arr[:, 0].astype(np.float)
acc = accuracy_score(answer, predict)
precision = precision_score(answer, predict)
recall = recall_score(answer, predict)
f1 = f1_score(answer, predict)
cm = confusion_matrix(answer, predict)
print("Accuracy: {:.3f}, Precision: {:.3f}, Recall: {:.3f}, F1: {:.3f}".format(acc, precision, recall, f1))
plt.rcParams["font.size"] = 18
cmd = ConfusionMatrixDisplay(cm, display_labels=[0,1])
cmd.plot(cmap=plt.cm.Blues, values_format='d')
plt.show()
結果は以下の通りです。
| Accuracy | Precision | Recall | F1 |
|---|---|---|---|
| 0.990 | 0.993 | 0.987 | 0.990 |
| 混同行列 | |||
 |
|||
| 単純なモデルにも関わらず思いのほか高い精度が得られました。Accuracy, Precision, Recallがどれも同じくらいの値となっていますので、誤報率$\alpha$の設定値も適切であったと結論できます。 |
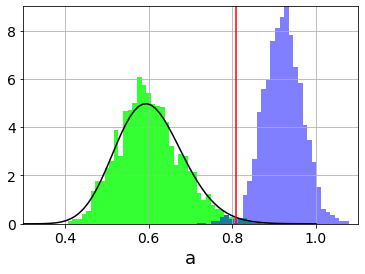
最後に、テストデータに対する異常値のヒストグラムを正常データと異常データに分けてプロットします。左の山が正常データ、右の山が異常データです。黒い実線は開発データから推定した$\hat{m}$と$\hat{s}$に対するカイ2乗分布です。赤の縦線は閾値$a_\text{th}$を表していますので、閾値のあたりを境に2つの分布が良く分けられていることがわかります。
おわりに
ちょっとした思い付きで計算して記事を書いてみたのですが、個人的には思いのほか面白くなって記事も長くなってしまいました。今回試したのは人間が見れば簡単に見分けられるような簡単なタスクでしたが、正直ここまで精度が高くなるとは思っておらず驚きました。異常検知モデル自体は単純なものですので、USEの性能の高さが精度につながったのではないかと思います。その意味では、他のエンコーダーモデルでも同じ計算をして比較することも必要だったと感じています。余裕があれば、後から計算して書き足したいと思います。