TL;DR
- LLMの最適化手法であるDPOとその派生手法 (IPO, cDPO, RSO, KTO) について解説する
- trlライブラリとLoRAを用いて、それらの手法で日本語LLMを最適化し、性能を定量的に比較する
- 3.6BパラメータのLLMをVRAM40GBのGPU1枚で全パラメータをDPOで学習する方法も説明する
はじめに
Direct Policy Optimazation (DPO)は大規模言語モデル(LLM)の挙動を制御するポリシー最適化(文脈によってはアライメントとも呼ばれます)のための学習手法で、強化学習を用いたProximal Policy Optimization (PPO)に代わるものとして最近注目を集めています。
PPOに関しては、こちら
の記事で試してみましたので、今回はその続きとして、DPOとその派生手法を使って日本語LLMをファインチューニングしてみます。学習にはtrlライブラリのDPOTrainerを使用します。前回と同様に、指示文の中で語尾を指定し、それに従って返答できるかという単純なタスク設定を扱うことで、手法の簡便な定量評価を試みます。
ポリシー最適化手法解説
まず初めに、trlライブラリで現在使用可能な手法を中心に各種のポリシー最適化手法について解説します。
RLHF
GPT-3.5などのLLMの学習は以下の3段階で行われています。
- Pre-traininig: 大規模なコーパスを用いた言語モデルの事前学習
- Supervised Fine Tuning (SFT): 対話形式や指示・応答形式のデータセットを用いたファインチューニング
- Policy Optimization: 人間にとって好ましい応答をさせるためのファインチューニング (Reinforcement Learning with Human Feedback; RLHF)
3段階目のポリシー最適化は、SFTとは異なり、入力に対して決まった正解を与えるわけではなく、LLMの応答に対して何らかの評価を返して、評価が高くなるようにLLMのパラメータを更新するというものです。
ポリシー最適化の最適化関数は次のようなものです。
\underset{\pi_\theta}{\text{max}}\big\{ \mathbb{E}_{x\sim \mathcal{D}, \, y\sim \pi_\theta (\cdot|x)} \left[ r(x,y)\right]
-\beta \mathbb{D}_\text{KL} \left[ \pi_\theta (y|x) || \pi_\text{ref} (y|x)\right]\big\}
\tag{1}
各記号の意味は以下の通りです。
- $x\,$: 入力文(プロンプト)
- $\mathcal{D}\,$: 入力文のデータセット
- $y\,$: 応答文
- $\pi_\theta (y|x)\,$: 学習対象のLLM。入力文$x$が与えられたときに応答文$y$が生成される条件付確率。
- $\theta\,$: 学習で更新されるパラメータ
- $\pi_\text{ref} (y|x)\,$: 参照モデル
- $r(x,y)\,$: 入力文$x$と応答文$y$に対する評価(報酬)関数
- $\mathbb{E}_{x\sim \mathcal{D}, \, y\sim \pi_\theta (\cdot|x)}\,$: $\mathcal{D}$からサンプルした$x$と$\pi_\theta (\cdot|x)$からサンプルした$y$に対する期待値
- $\mathbb{D}_\text{KL} \left[ \pi_\theta (y|x) || \pi_\text{ref} (y|x)\right]\,$: $\pi_\theta (y|x)$と$\pi_\text{ref} (y|x)$を$y$に関する確率分布とみなした時の、両者のKLダイバージェンス
- $\beta\,$: 正のハイパーパラメータ
評価・報酬関数$r(x,y)$としては、人間からのフィードバックなどのデータセットを使って学習した別のモデルが使われることが多いです。
(1)式における$r$の期待値の項の意味は、LLMが生成した結果の評価・報酬が高くなるようにLLMを最適化するということです。しかし、それだけだと評価を高めるための抜け道が存在する場合、文法的にはめちゃくちゃだけど評価だけは高いというようなテキストの生成を行うように学習が進んでしまうので、それを防ぐために第2項のKLダイバージェンスが加えられています。
KLダイバージェンスは2つの分布の間の距離を与えるもので、分布が一致すれば0、異なっていれば正の値を取ります。したがって、学習対象のLLM $\pi_\theta (y|x)$と参照モデル $\pi_\text{ref} (y|x)$の生成確率の分布が違い過ぎると、第2項の絶対値が大きくなりペナルティが与えられるということになります。参照モデルとして自然な文章を生成できるようなモデルを使えば、学習したモデルは自然な文章を生成する能力を保持しながら報酬が高い振る舞いをするようになります。
KLダイバージェンスの項を具体的に書くと、
\mathbb{D}_\text{KL} \left[ \pi_\theta (y|x) || \pi_\text{ref} (y|x)\right]
= \mathbb{E}_{x\sim \mathcal{D},\, y\sim \pi_\theta (\cdot|x)} \left[ \log \frac{\pi_\theta (y|x)}{\pi_\text{ref} (y|x)}\right]
\tag{2}
となります。($x$に対する期待値はここには含めないのが自然な定義ですが、(1)式を簡潔かつ、よく見る表式に合わせるため、このように定義しておきます。)
さて、(1)式は$\pi_\theta (y|x)$からサンプルした応答文$y$に対する期待値として書かれていますが、具体的なトークン列としてサンプルした時点でモデルパラメータ$\theta$で微分することはできなくなってしまいます。したがって、深層学習モデルの学習で通常行われる、最適化関数(損失関数)のモデルパラメータについての微分を逆誤差伝播で求めてパラメータを更新するという手法は適用できず、強化学習の手法、特にPPOを用いた最適化が行われるのが主流でした。
PPOはOpenAIのLLMの学習に使われている強力な手法ではありますが、計算コストの高さや(特に大きなモデルに対する)学習の不安定さなどの課題があり、実行するのは敷居が高い手法でした。
PPOはtrlライブラリにPPOTrainerとして実装されていますが、前回の記事で試してみたところ、確かに計算コストが高く、学習に長い時間を要しました。
DPO
DPOはPPOに代わるポリシー最適化手法として2023年5月に発表された手法で、強化学習を用いず通常の教師あり学習と同じような手順で(1)式の最適化を行えるというものです。
そのためにRLHFの問題設定に加えていくつかの仮定を置きます。RLHFにおいては報酬関数$r(x,y)$のモデリングに対しては何の仮定もしていなかったのですが、DPOではBradley-Terryモデルにより定式化されていると仮定します。
p^{\ast} (y_1 \succ y_2 |x) = \frac{\exp \!\left[ r(x, y_1) \right]}{\exp \!\left[ r(x, y_1) \right] + \exp \!\left[ r(x, y_2) \right]}
\tag{3}
ここで、 $p^{\ast} (y_1 \succ y_2 |x)$は入力文$x$に対する応答が2つ与えられたとき、そのうち$y_1$の方が好ましい確率を意味しています。この $p^{\ast} (y_1 \succ y_2 |x)$が右辺の表式で報酬関数$r(x,y)$を通じて表現されるというのが仮定です。要するに報酬$r$が高い応答の方が好ましいと判定されるということなので、自然なモデリングです。右辺はシグモイド関数$\sigma (x)$を用いて、$\sigma \left(r(x, y_1) - r(x, y_2)\right)$と書くことができます。
さて、このモデルを学習させるために、入力文$x$と好ましい応答$y_w$、好ましくない応答$y_l$から成るデータセット$\mathcal{D}_\text{pair} = \big\{ x^{(i)}, y_w^{(i)}, y_l^{(i)}\big\}_{i=1}^N$があるとします。添え字の$w$はwin、$l$はloseの頭文字です。
報酬関数を学習するための最適化関数は通常のシグモイド損失で
L_\text{reward} = -\mathbb{E}_{(x,y_w, y_l)\sim \mathcal{D}_\text{pair}} \log \sigma \!\left(r(x, y_w) - r(x, y_l)\right)
\tag{4}
と書けます。
DPOの核となるアイディアは、この報酬関数の最適化関数(4)をLLMの最適化関数に置き換えてしまうということです。そのために、元のLLMのポリシー最適化のための最適化関数(1)には厳密解
\pi (y|x) = \frac{1}{Z(x)} \pi_\text{ref} (y|x) \exp \left( \frac{1}{\beta} r(x,y)\right)
\tag{5}
が存在することを使います。$Z(x)=\sum_y \pi_\text{ref} (y|x) \exp \left( \frac{1}{\beta} r(x,y)\right)$は規格化のための分配関数です。1
この解が実際に最適化関数(1)を最大化することの証明はDPO論文のAppendixに与えられています。
厳密解が存在するなら、わざわざPPOやDPOのアルゴリズムを工夫して手のかかる数値計算を行わなくてもよいのではと思う人がいるかもしれませんが、これはあくまで形式解であって、実用には向きません。理由は分配関数$Z(x)$があらゆる応答テキスト$y$の和で与えられているため、これを計算することは現実的ではないからです。棄却サンプリング法などの手法を使えば規格化定数がわからない確率分布からのサンプリングも可能ですが、系列データである$y$を生成するという今の問題設定ではそれも難しいと思います。
DPO導出の次の重要なステップは、(5)式を$r$について解くことです。
r(x,y) = \beta \log \frac{\pi (y|x)}{\pi_\text{ref} (y|x)} + \beta \log Z(x)
\tag{6}
すでに述べたように分配関数$Z(x)$は実際には計算できない未知の関数なのですが、この(6)式を報酬関数の最適化関数(4)に代入すると、$Z(x)$がキャンセルして消えてしまいます。
L_\text{reward} = -\mathbb{E}_{(x,y_w, y_l)\sim \mathcal{D}_\text{pair}} \log \sigma \!\left(\beta \log \frac{\pi (y_w|x)}{\pi_\text{ref} (y_w|x)} - \beta \log \frac{\pi (y_l|x)}{\pi_\text{ref} (y_l|x)}\right)
\tag{7}
この最適化関数はLLMのみで表現されていますので、LLMを学習するための損失関数とみなすことができます。それを明確にするため、$\pi$を学習対象のLLM $\pi_\theta$で置き換えたものを$L_\text{DPO}$と呼ぶことにしましょう。
L_\text{DPO} = -\mathbb{E}_{(x,y_w, y_l)\sim \mathcal{D}_\text{pair}} \log \sigma \!\left(\beta \log \frac{\pi_\theta (y_w|x)}{\pi_\text{ref} (y_w|x)} - \beta \log \frac{\pi_\theta (y_l|x)}{\pi_\text{ref} (y_l|x)}\right)
\tag{8}
好ましい応答をする尤度(正確には参照モデルとの対数尤度比)を高く、好ましくない応答の尤度を低くしようとする損失関数となっています。
この損失関数は参照モデルにも依存しているという点を除けば、通常の教師あり学習の損失関数と同様の形式であり、SFTと同じ要領で学習を行うことができます。
DPOはtrlライブラリのDPOTrainerでloss_type="sigmoid"(デフォルト設定)とすることで簡単に使うことができます。具体的な方法は後から説明します。
IPO (ΨPO)
DPOは報酬関数の準備と強化学習の実行の両方を不要にした画期的な手法ですが、学習データに過適合しやすいという問題が指摘されていました。
Google DeepMindの論文 "A General Theoretical Paradigm to Understand Learning from Human Preferences"では、DPOを一般化したΨPOを導入したうえで、DPOが過適合しやすい原因を明らかにし、ΨPOの特殊ケースとしてIPOを提案しています。
まず、$\Psi (x)$という定義域が$[0,1]$である非減少実関数を考えます。この関数を使って、(1)式で与えられるPPOおよびDPOの最適化目的関数を次のように一般化します。
\underset{\pi_\theta}{\text{max}}\big\{ \mathbb{E}_{x\sim \mathcal{D},\, y \sim \pi_\theta (\cdot|x),\, y^\prime \sim \mu (\cdot|x)} \left[ \Psi \left( p^{\ast} (y \succ y^\prime |x)\right)\right]
-\beta \mathbb{D}_\text{KL} \left[ \pi_\theta (y|x) || \pi_\text{ref} (y|x)\right]\big\}
\tag{9}
ここで、$\mu (y^\prime|x)$は$\pi_\theta (y|x)$とは異なる何らかのLLM(より正確には$y^\prime$を生成する何らかのポリシー)です。$p^{\ast}$は(3)式で与えられるBradley-Terryモデルです。第1項の期待値の中身の$\Psi \left( p^{\ast} (y \succ y^\prime |x)\right)$は報酬$r(x,y)$に関する増加関数ですので、上式はKL項の制約の下で報酬を最大化するという意味で(1)式と目的は同じであり、関数$\Psi$を自由に変えられるという意味で(1)式の一般化となっています。
実際、$\Psi (x) = \log \frac{x}{1-x}$(シグモイド$\sigma(x)$の逆関数)とすると、(9)式は$\pi_\theta$に依存しない定数を除いて(1)式と一致します。
(9)式で与えられるΨPOの最適化関数は報酬$r(x,y)$に依存していますので、DPOと違って直接最適化することはできませんが、$\Psi (x)$の具体形をうまく選んでやると、直接最適化可能な目的関数が得られます。それがIPOです。そして、IPOはDPOの過適合しやすいという問題を回避したものになっています。
まず、DPOがなぜ過適合しやすいのかを説明します。
DPOでは好ましい応答$y_w$と好ましくない応答$y_l$を学習データに用いますので、(9)式における$p^{\ast} (y \succ y^\prime |x)$に対する正解ラベルは0または1の値を取ることになります。
(3)式のBradley-Terryモデルはシグモイド関数で与えられていますので、$p^{\ast}=0,1$となるのは、シグモイドの引数である$r(y)-r(y^\prime)$が$\pm \infty$の時です。もちろん、数値計算上無限大は現れませんし、そもそもDPOの計算では報酬$r$は実際には計算されていない仮想的な概念ですが、仮想的に$|r(y)|$が非常に大きくなってしまうということです。すると、DPOのもともとの最適化関数(1)式において、第1項に比べて第2項のKL項が相対的に小さくなってしまいます。したがって、KL項の正則化が効かなくなって、学習データに過適合してしまうというわけです。
つまり、過適合の原因はシグモイド関数の値域が閉区間$(0,1)$であることです。同じことですが、DPOの$\Psi$関数であるシグモイドの逆関数$\Psi_\text{DPO} (x) = \log \frac{x}{1-x}$を使って説明すると、$\Psi_\text{DPO} (x)$が非有界で、$x\to 0, 1$の時に$\Psi_\text{DPO} (x) \to \pm \infty$となることが原因です。
そこで、そのような性質を持たない単純な関数として、恒等関数 (Identity function) $\Psi (x) =x$を用いるのがIPOです。
この$\Psi$を(9)式に代入すると、IPOの目的関数
\underset{\pi_\theta}{\text{max}}\big\{ \mathbb{E}_{x\sim \mathcal{D},\, y \sim \pi_\theta (\cdot|x),\, y^\prime \sim \mu (\cdot|x)} \left[ p^{\ast} (y \succ y^\prime |x)\right]
-\beta \mathbb{D}_\text{KL} \left[ \pi_\theta (y|x) || \pi_\text{ref} (y|x)\right]\big\}
\tag{10}
が得られます。このままでは、依然として報酬関数$r$に陽に依存しているので直接最適化はできないのですが、DPOと同様に厳密解を援用することで、直接最適化のアルゴリズムを導くことができます。
導出はDPOに比べて複雑で少し長くなるので省略します。気になる方は原論文を参照ください。最終的な最適化関数は
L_\text{IPO} = \mathbb{E}_{(x,y_w, y_l)\sim \mathcal{D}_\text{pair}}
\left(\log \frac{\pi_\theta (y_w|x)}{\pi_\text{ref} (y_w|x)} - \log \frac{\pi_\theta (y_l|x)}{\pi_\text{ref} (y_l|x)} -\frac{1}{2\beta} \right)^2
\tag{11}
となります。DPOはシグモイド損失のような形であったのに対して、IPOは2乗誤差のような形をしています。
DPOではシグモイドの引数全体が正則化係数$\beta$に比例していたため、$\beta$の値の大きさに関わらず、好ましい応答の対数尤度比を大きく、好ましくない応答の対数尤度比を小さくしようと学習が進むので、過適合しやすかったのですが、IPOでは2つの対数尤度比の値が$1/(2\beta)$だけ離れた状態を最適とするのでDPOと比べて過適合は起きにくいということが関数形からわかります。
IPOはDPOTrainerでloss_type="ipo"とすれば使うことができます。
ちなみに、DPOTrainerにおけるIPOの実装は最初間違ったものでした。
こちら
Preference Tuning LLMs with Direct Preference Optimization Methods
の記事では、DPO, IPO, KTOを$\beta$パラメータを変えながら比較しているのですが、最初に公開されたときはIPOの性能が劣るという結論でした。上記の加筆修正版の記事の最初に書いてあるように、その後IPOの実装に間違いが見つかり、修正して実験をやり直したところ、IPOはDPOと同程度の性能になったとのことです。
IPOの実装の間違いはこちらのPRにより、trl==0.7.11では修正されています。
cDPO
上記のIPOの解説でDPOが報酬に過適合しやすい理由はBradley-Terryモデルに与えられる正解ラベルが0か1であることだと述べました。つまり、データセットにおいて好ましい応答$y_w$と好ましくない応答$y_l$がはっきりと決められていることが原因であると言えます。そこで、IPOとは別の過適合を防ぐためのシンプルなアプローチとして、ラベルにノイズを入れることがこちらのノートで提案されました。分類問題でよく用いられる正則化手法のラベルスムージングと同じ考え方です。cDPOはconservative DPOの略です。
具体的にはラベルスムージングの確率$\epsilon$を設定して、損失関数を
L_\text{DPO}^\epsilon = (1-\epsilon) L_\text{DPO} (\theta; y_w, y_l) + \epsilon L_\text{DPO} (\theta; y_l, y_w)
\tag{12}
とするだけです。第1項の$L_\text{DPO} (\theta; y_w, y_l)$は(8)式で与えられるDPOの損失関数そのものです。第2項の$L_\text{DPO} (\theta; y_l, y_w)$は好ましい応答と好ましくない応答を入れ替えたものです。
DPOTrainerではloss_type="sigmoid"としたうえで、label_smoothing引数に0より大きく0.5未満の値を与えることで使用できます。(公式ドキュメントの一部にはloss_type="cdpo"とすると書いてありますが、現在のバージョンではその指定の仕方は無効です。)
RSO
次に、DPOTrainerでも使用できるhinge lossを導入した論文"Statistical Rejection Sampling Improves Preference Optimization"を紹介します。
DPOの最適化関数(8)は結局のところ、好ましい応答と好ましくない応答のペアのデータセットを準備して、前者の生成確率が高く、後者の生成確率が低くなるように教師あり学習するというものでした。そのような直接的な考えに基づいた手法はDPOよりも前に提案されており、SLiCでは以下のようなヒンジ関数$\text{max}(0,x)$を使った損失関数が使われています。
L_\text{SLiC} = \mathbb{E}_{(x,y_w, y_l)\sim \mathcal{D}_\text{pair}} \text{max} \left(0, \delta -\log \pi_\theta (y_w|x) + \log \pi_\theta (y_l|x) \right)
-\lambda \mathbb{E}_{(x,y_\text{ref})\sim \mathcal{D}_\text{ref}} \log \pi_\theta (y_\text{ref}|x)
\tag{13}
$\delta$は正の定数でマージンを表しています。第2項は過適合を防ぐための正則化項で通常のSFTと同じ損失関数です。
この損失関数には参照モデルが登場しない代わりに、ペアデータセット$\mathcal{D}_\text{pair}$と通常のSFTのためのデータセット$\mathcal{D}_\text{ref}$を同時に学習しなくてはなりません。
RSO論文では、DPOの損失関数に寄せた形として、以下のような損失関数を提唱しています。
L_\text{RSO} = \mathbb{E}_{(x,y_w, y_l)\sim \mathcal{D}_\text{pair}} \text{max} \left(0, 1 -\left[ \beta \log \frac{\pi_\theta (y_w|x)}{\pi_\text{ref} (y_w|x)} -\beta \log \frac{\pi_\theta (y_l|x)}{\pi_\text{ref} (y_l|x)} \right] \right)
\tag{14}
正則化パラメータ$\beta$の逆数がマージンの役割を果たします。
この損失関数はDPOやIPOのように元のRLHFの最適化関数(1)から数学的に導かれたものではなく、ヒューリスティックに導入されたものです。
この損失関数はDPOTrainerでloss_type="hinge"とすることで使用できます。
RSO論文の貢献はタイトルからわかるように、この損失関数を提案したことだけではなく、棄却サンプリング法 (rejection sampling)を使って、より良いペアデータセットを選別して最適化のプロセスを改善するということです。
RLHFにおいて報酬モデルを学習させるためのデータセット、あるいはDPOやIPOで直接最適化に使われるデータセット$\mathcal{D}_\text{pair}$の応答テキストというのは、人間が書いたものか、何らかのLLMが出力したものです。これらの応答テキストを生成するためのポリシーというのは、学習対象のLLMが最適化された後のポリシーとは異なります。このギャップを埋めようというのがRSOの目的です。
すなわち、最適化が終わった後のLLMが生成するテキストにより近いテキストでLLMを学習させようということです。単純に考えると、未来の自分自身が生成するであろうテキストで現在の自分を学習するということになるので無理な話に思えますが、形式的な厳密解(5)を活用することで可能になります。
手順としては、まずデータセット$\mathcal{D}_\text{pair}$(論文ではデータセット$\mathcal{D}_\text{hf}$と書かれています)を使って、Bradley-Terryモデル(3)に対応するランキングモデルを学習します。報酬のベースラインを定義すればランキングモデルから報酬関数$r(x,y)$を得ることができます。(あるいはRLHFと同じようにデータから直接的に報酬関数を学習してもいいでしょう。)
こうして得られた報酬関数を厳密解(5)に代入すれば、最適化された後のLLMが形式的には得られます。すでに述べたように分配関数$Z(x)$を計算することは現実的には不可能なので、厳密解を通常のLLMのように生成に使うことは難しいですが、棄却サンプリング法を使えば厳密解の確率分布に従うデータセットを構成することができます。ここでいう棄却サンプリング法は、規格化定数がわかっていない確率密度関数からの乱数生成に使われる手法のことです。具体的には、提案分布として$\pi_\text{ref} (y|x)$(論文では$\pi_\text{SFT} (y|x)$と書かれている)を用いて、そこからサンプルを生成したうえで、通常の棄却サンプリング法の手続きに従って採択か棄却かを決めることで、確率分布$\pi (y|x) \propto \pi_\text{ref} (y|x) \exp (r(x,y)/\beta)$に従うデータセットを作成します。
こうして作成したデータセットを用いて、(14)式の最適化を行うのがRSOです。
ただし、棄却サンプリング法を使う部分はデータセットを作成する手段ですので、DPOTrainerには実装されていません。DPOTrainerに実装されているのはあくまで(14)式の損失関数です。その意味で、以下ではhinge lossを使う最適化手法をRSOとは呼ばずにhingeと呼ぶこととします。
KTO
最後にKTO (Kahneman-Tversky Optimazation)について解説します。
KTOはカーネマンとトベルスキーによるプロスペクト理論に着想を得た手法です。
プロスペクト理論は人間の意思決定に関する理論で、以下のような話が有名です。
- 「確実に100万円貰える」という場合と「確率50%で200万円貰えるが、確率50%で何も貰えない」という場合のどちらかを選べと言われると、貰える金額の期待値はどちらも同じだが、前者を選ぶ人が多い
- 貰えるというのを負債に置き換えて、「確実に負債が100万円増える」という場合と「確率50%で負債が200万円増えるが、確率50%で何も変わらない」という場合を考えると、今度は後者を選ぶ人が多い
このように利益と損失に対する人間の反応が対称ではないというのが、プロスペクト理論の主張するところの一つであり、KTOの技術レポートによると、RLHFやDPOは報酬に対する非対称性を備えており、プロスペクト理論に沿ったものになっているそうです。
KTOが主に依拠しているのは、「人は富そのものでなく、富の変化量から効用を得る」というプロスペクト理論のもう一つの主張です。すなわち、利益や損失を絶対量としてとらえるのではなく、基準からの変化量として相対的にとらえる、ということです。
RLHFの最適化関数(1)においては、入力$x$に対する応答$y$の価値$r(x,y)$そのものを最大化しようとしていましたが、プロスペクト理論の主張に沿うと、価値$r(x,y)$というのは相対的なものなので、基準からの差に着目するべき、ということになります。
価値の基準としては、色々な応答$y$に対する平均値を採用します。したがって、$r(x,y)$の代わりに
r(x,y) - \mathbb{E}_{y \sim \pi (\cdot|x)} \left[ r(x,y)\right]
を最大化するということになります。ここに、最適化問題の厳密解から得られる(6)式を代入すると、DPOの導出と同じように分配関数$Z(x)$がキャンセルして、次式が得られます。
\beta \log \frac{\pi (y|x)}{\pi_\text{ref} (y|x)} - \beta \mathbb{E}_{y \sim \pi (\cdot|x)} \left[ \log \frac{\pi (y|x)}{\pi_\text{ref} (y|x)}\right]
\tag{15}
KTOの技術レポートでは第2項をKLダイバージェンスで書き換えていますが、この記事では(2)式のように$y$だけでなく$x\sim \mathcal{D}$に対しても期待値を取ったものをKLダイバージェンスと定義しているので、ここではKLダイバージェンスで書き換えてはいません。
今、学習データ$\mathcal{D}_\text{KTO}$として入力$x$とそれに対する好ましい応答$y_w$のペア$(x,y_w)$と、入力と好ましくない応答$y_l$のペア$(x,y_l)$があるとすると、$y_w$に対しては(15)式の相対価値を最大化、$y_l$に対しては最小化すればいいので、KTOの損失関数は以下のようになります。
L_\text{KTO} = \mathbb{E}_{(x,y)\sim \mathcal{D}_\text{KTO}} \left[ 1 - \hat{h} (x,y)\right]
\tag{16}
ここで、$\hat{h}$は(15)式の相対価値をシグモイドに通したものです。
\hat{h}(x,y) = \begin{cases}
\sigma \left( \beta \log \frac{\pi_\theta (y|x)}{\pi_\text{ref} (y|x)} - \beta \mathbb{E}_{y \sim \pi_\theta (\cdot|x)} \left[ \log \frac{\pi_\theta (y|x)}{\pi_\text{ref} (y|x)}\right]\right) \ \text{if}\ y=y_w \\
\sigma \left( \beta \mathbb{E}_{y \sim \pi_\theta (\cdot|x)} \left[ \log \frac{\pi_\theta (y|x)}{\pi_\text{ref} (y|x)}\right] - \beta \log \frac{\pi_\theta (y|x)}{\pi_\text{ref} (y|x)} \right) \ \text{if}\ y=y_l
\end{cases}
シグモイドに通しているのは、最適化計算を行いやすくする目的だと思われます。
好ましくない応答に対しては損失を大きくしたいので、シグモイドの中身の符号をひっくり返しています。
KTOがDPOなどの他手法に対して優位な点は、学習データセットが好ましい応答と好ましくない応答のペアである必要がないということです。DPOの学習データセット$\mathcal{D}_\text{pair}$は一つの入力$x$に対する応答として好ましいものと好ましくないものの両方のペアが必要でした。一方、KTOにおいては、一つの入力$x$に対する応答としては好ましいものと好ましくないもののどちらか一方があれば上記の損失関数を計算することができます。
優劣のペアの応答データを集めることに比べれば、単一の評価を集めることは非常に簡単ですので、実応用を考えるとKTOの性質は大きなアドバンテージとなります。
ただし、trlライブラリのDPOトレーナーで使用できるKTOの実装は、DPOと同じペア形式のデータセットを仮定したものになっています。すなわち実装されている損失関数は(16)式ではなく、
L_\text{KTO(pair)} = \mathbb{E}_{(x,y_w,y_l)\sim \mathcal{D}_\text{pair}} \left[ 2 - \hat{h} (x,y_w)- \hat{h} (x,y_l)\right]
\tag{17}
ということだと思います。これは、DPOTrainerという同じクラスに実装されている都合で、公式ドキュメントにはペアではないデータに対応したKTOはKTOTrainerとして別クラスに実装されることになるだろう、というようなことが書いてあります。
環境
実験はGoogle Colab (Pro+)上でA100GPU (Syetem RAM 83.5GB, GPU RAM 40.0GB)を使用して行いました。
ライブラリのインストール
transformersのバージョンは前回の実験時と揃えました。
deepspeedとflash-attnはフルファインチューニングを行う場合には必要となります。
!pip install -U transformers==4.36.2
!pip install datasets accelerate bitsandbytes peft sentencepiece
!pip install trl
!pip install deepspeed ninja
!pip install flash-attn --no-build-isolation
Pythonおよび主要ライブラリのバージョン
Python 3.10.12
accelerate 0.26.1
bitsandbytes 0.42.0
datasets 2.16.1
deepspeed 0.12.6
flash-attn 2.5.0
ninja 1.11.1.1
peft 0.8.1
torch 2.1.0+cu121
transformers 4.36.2
trl 0.7.10
ただし、trlの上記のバージョンではDPOTrainerのIPOの部分に間違いがあることが判明したので、IPOに関しては後からtrl==0.7.11で計算をやり直しました。
trl==0.7.11は記事執筆時点でpipインストールできる最新版です。
以下では明示しませんが、各ノートブックでgoogle driveをマウントしているものとします。
問題設定
ポリシー最適化の効果を簡単に定量的に確認できるような問題設定として、プロンプトの指定で返答の語尾を変えさせるということを考えます。
具体的には既存のデータセットのプロンプトの中に### Tagというフィールドを追加して、そこで指定した顔文字で、以下のように返答部分の語尾を指定します。
| tag | 語尾 |
|---|---|
| 😐 | (変化なし) |
| 🫡 | ござる |
| 🤪 | おっぱっぴー |
| 🤓 | ござるよドゥフフw |
🫡と🤓で「ござる」が重複しているのは、タスクを難しくするためです。
日本語dollyデータセットdatabricks-dolly-15k-jaと、その語尾を「ござる」に変えた通称ござるデータセットdatabricks-dolly-15k-ja-gozaruを使ってデータセットを作成しました。具体的なデータ作成手順については前回の記事を参照ください。
データの中身は例えば以下のようなものです。
### Instruction
Slackのエチケットとして、どのようなルールがあるのでしょうか?
### Tag
🤓
### Answer
Slackのエチケットは職場によって大きく異なるため、一般的なガイドラインを示すことは困難ですでござるよドゥフフw。しかし、Slackを使用するほとんどの職場には、いくつかの共通ルールがありますでござるよドゥフフw。例えば、勤務時間外にメッセージを書いている場合は、勤務時間内に送信するようにスケジュールするのがよいでしょうでござるよドゥフフw。メッセージに返信する場合は、新しいスレッドを立てるよりも、スレッドで返信するほうがよいでござるよドゥフフw。
このようなデータセットを用いてLLMをSFTし、タグの指示で語尾を変えて返答するように訓練します。別に用意したテストデータを使って指示に従う割合を精度として算出とします。さらにSFT後のモデルをDPOなどのポリシー最適化により指示に従うように追加で学習することで、精度がどれだけ向上するかを見ることによりポリシー最適化手法の効果を定量的に評価することとします。
LLMとしては事前学習済みのLINEのLLM japanese-large-lm-3.6bを使用し、上で説明したデータセット14,126件を用いてSFTしました。テストデータは200件のdollyデータに4種類のタグを付与した計800件です。精度を算出する際には、😐に対しては応答の中に3種類の語尾のいずれも現れなければ正解、他のタグに対しては該当の語尾のみが現れていれば正解としました。
SFTの実際の学習手順は前回の記事で説明したのでここでは省略します。フルファインチューニングで2エポック学習したあとの精度(全体正解率)は0.666でした。
このSFTモデルをもとにDPO, cDPO, IPO, hinge, KTOによるポリシー最適化をそれぞれ行い、結果の比較を行います。
データセット準備
trlライブラリのDPOTrainerを使うためには、入力文$x$と好ましい応答$y_w$、好ましくない応答$y_l$の3つが組となったデータセットが必要です。
入力文と好ましい応答についてはSFT用のデータセットをそのまま使用し、好ましくない応答に関しては入力文の中で指定された語尾とは違う語尾をランダムに選んで、その語尾をつけた応答を使用することとします。
まず、SFT用のデータセットを読み込みます。このデータセットの作成方法については前回の記事を参照ください。
from datasets import load_from_disk
# 作成済みのSFT用trainデータセット読み込み
dataset = load_from_disk("train_dataset.hf")
print(dataset)
# Dataset({
# features: ['category', 'index', 'output', 'input', 'instruction', 'tag'],
# num_rows: 14126
# })
複数カラムに分かれていますが、'instruction', 'input', 'tag'は入力文の構成要素で、'output'が正解の応答文です。'category'と'index'は元のdollyデータセットにあるカラムで、categoryは使用しないので不要ですが、indexは好ましくない応答との紐づけに使用します。
DPOTrainerのためのデータセットは入力文に相当する'prompt'、好ましい応答の'chosen'、そして好ましくない応答の'reject'の3つのカラムが必要です。まず、SFT用データセットから'prompt'と'chosen'を作成します。
def format_prompt(sample):
instruction = f"### Instruction\n{sample['instruction']}"
input = f"### Context\n{sample['input']}" if len(sample["input"]) > 0 else None
tag = f"### Tag\n{sample['tag']}"
# 3つを結合してpromptを作成
sample["prompt"] = "\n\n".join([i for i in [instruction, input, tag] if i is not None])
# 正解のoutputをchosenとする
sample["chosen"] = f"### Answer\n{sample['output']}"
return sample
dataset = dataset.map(format_prompt, remove_columns=["category", "instruction", "input", "output"])
次に'reject'を作成するために、元の日本語dollyデータセットとござるデータセットをindexカラムをキーにして結合します。
from datasets import load_dataset, Dataset
import pandas as pd
# 日本語dollyデータセットとござるデータセットを読み込む
dataset_dolly = load_dataset("kunishou/databricks-dolly-15k-ja", split="train")
dataset_gozaru = load_dataset("bbz662bbz/databricks-dolly-15k-ja-gozaru", split="train")
# 一度、pandas DataFrameに変換してから、indexをキーにマージする
dataset_df = pd.DataFrame(dataset)
dolly_df = pd.DataFrame(dataset_dolly)[["index", "output"]].rename(columns={"output": "dolly_output"})
gozaru_df = pd.DataFrame(dataset_gozaru)[["index", "output"]].rename(columns={"output": "gozaru_output"})
_df = pd.merge(dolly_df, gozaru_df, on="index")
dataset_df = pd.merge(dataset_df, _df, on="index", how="left")
# datasetに戻す
dataset = Dataset.from_pandas(dataset_df)
print(dataset)
# features: ['index', 'tag', 'prompt', 'chosen', 'dolly_output', 'gozaru_output', '__index_level_0__'],
# num_rows: 14126
最後に、各行においてpromptで指定されたタグ以外のタグをランダムに選び、そのタグに該当する応答文を'dolly_output'か'gozaru_output'から作成し、'rejected'とします。
import random
tag_list = ["😐", "🫡", "🤪", "🤓"]
tag_rule = {
"🫡": lambda text: text,
"🤪": lambda text: text.replace("ござる", "おっぱっぴー"),
"🤓": lambda text: text.replace("ござる", "ござるよドゥフフw"),
}
def make_rejected_output(sample):
index = sample["index"]
designated_tag = sample["tag"]
# 入力で指定されたtag以外のtagからランダムに選んだものをrejected用にする
other_tags = [t for t in tag_list if t != designated_tag]
rejected_tag = random.choice(other_tags)
if rejected_tag == "😐":
# 元のdolly-jaデータセットを使用
rejected_output = sample["dolly_output"]
else:
# ござるデータセットを使用
rejected_output = sample["gozaru_output"]
# 語尾をrejected_tagに合わせて改変
rejected_output = tag_rule[rejected_tag](rejected_output)
sample["rejected"] = f"### Answer\n{rejected_output}"
return sample
keep_cols = ['prompt', 'chosen', "rejected"]
remove_columns = [c for c in list(dataset.features) if c not in keep_cols]
dataset = dataset.map(make_rejected_output, remove_columns=remove_columns)
print(dataset)
# features: ['prompt', 'chosen', 'rejected'],
# num_rows: 14126
データセットの中身は例えば以下のようなものです。
- prompt
### Instruction
クリスマスに家族に振る舞える華やかなホリデー料理を3つ教えてください。
### Tag
🫡
- chosen
### Answer
ここでは、ホリデーシーズンのお祝いの食事を3つご紹介します:
* プライムリブとヨークシャープディングは、とても伝統的な料理でござる。
* ターキー、マッシュポテト、クランベリー、スタッフィングは、カラフルでおいしいアメリカの伝統的な料理でござる。
* 仔羊のモモ肉とミントソースの組み合わせも元気いっぱいでござる。
- rejected
### Answer
ここでは、ホリデーシーズンのお祝いの食事を3つご紹介します:
* プライムリブとヨークシャープディングは、とても伝統的な料理です。
* ターキー、マッシュポテト、クランベリー、スタッフィングは、カラフルでおいしいアメリカの伝統的な料理です。
* 仔羊のモモ肉とミントソースの組み合わせも元気いっぱいです。
ここでは、chosenとrejectedは語尾が違うだけで応答の中身は同じものとしていますが、必ずしもそうである必要はなく、例えばrejectedとしてはSFTモデルの間違った語尾の応答を使うというようなことをしてもいいかもしれません。また、RSOのような手法で"より良い"データセットを作ることも効果的かもしれませんが、今回の実験では単純なデータセットを使用します。
DPOは過適合しやすいと言われていますので、学習時に検証データに対する損失もモニターすることにします。そのためにデータを分割して保存します。
indices = list(range(len(dataset)))
random.shuffle(indices)
val_size = 2000
val_indices = indices[:val_size]
train_indices = indices[val_size:]
val_dataset = dataset.select(val_indices)
train_dataset = dataset.select(train_indices)
print(len(train_dataset)) # 12126
print(len(val_dataset) # 2000
# 保存
train_dataset.save_to_disk("dpo_train_dataset.hf")
val_dataset.save_to_disk("dpo_val_dataset.hf")
実験
学習手順
DPOTrainerを使ったポリシー最適化の実行手順をDPOの場合を例に説明します。
データセット読み込み
from datasets import load_from_disk
train_dataset = load_from_disk("dpo_train_dataset.hf")
eval_dataset = load_from_disk("dpo_val_dataset.hf")
トークナイザーの立ち上げ
from transformers import AutoTokenizer
model_name = "line-corporation/japanese-large-lm-3.6b"
tokenizer = AutoTokenizer.from_pretrained(model_name, use_fast=False)
DPOTrainerでは入力するデータの最大系列長とプロンプト部分の最大系列長を指定する必要があるので、学習データの各部分の最大系列長を調べておきます。
def measure_length(sample):
sample["prompt_len"] = len(tokenizer(sample["prompt"])["input_ids"])
sample["chosen_len"] = len(tokenizer(sample["chosen"])["input_ids"])
sample["rejected_len"] = len(tokenizer(sample["rejected"])["input_ids"])
return sample
dataset_len = train_dataset.map(measure_length)
print(max(dataset_len["prompt_len"])) # -> 162
print(max(dataset_len["chosen_len"])) # -> 166
print(max(dataset_len["rejected_len"])) # -> 188
プロンプトの最大系列長は162、全体の最大系列長は162+188=350でした。
SFT済みのモデルを読み込みます。
DPOによる学習はLoRAで行うこととしますので、peftを使って設定を行います。
import torch
from transformers import AutoModelForCausalLM
from peft import LoraConfig, get_peft_model
sft_model_path = "./line_sft" # 学習済みSFTモデルのパス
model = AutoModelForCausalLM.from_pretrained(
sft_model_path,
)
# LoRA設定
target_modules = ["query_key_value", "dense", "dense_h_to_4h", "dense_4h_to_h"]
lora_config = LoraConfig(
target_modules=target_modules,
r=16,
lora_alpha=32,
lora_dropout=0.05,
bias="none",
task_type="CAUSAL_LM",
)
model = get_peft_model(model, lora_config)
次にDPOTrainerを立ち上げます。
PPOTrainerとは違い、DPOTrainerに渡すtraining_argsはtransformersライブラリのTrainerクラスで使用するTrainingArgumentsです。したがって、Trainerクラスで使用可能だった機能はDPOTrainerクラスでも使用可能です。
from transformers import TrainingArguments
from trl import DPOTrainer
output_dir="./line_dpo_1"
training_args = TrainingArguments(
output_dir=output_dir,
overwrite_output_dir=True,
per_device_train_batch_size=2,
gradient_accumulation_steps=128,
per_device_eval_batch_size=16,
learning_rate=1e-5,
weight_decay=0.01,
num_train_epochs=2,
lr_scheduler_type="constant_with_warmup",
warmup_steps=10,
fp16=True,
evaluation_strategy="steps",
save_strategy="steps",
save_steps=32,
logging_steps=8,
eval_steps=8,
load_best_model_at_end=True,
save_safetensors=False,
save_only_model=True,
remove_unused_columns=False,
)
dpo_trainer = DPOTrainer(
model=model,
args=training_args,
beta=0.3,
train_dataset=train_dataset,
eval_dataset=eval_dataset,
tokenizer=tokenizer,
max_prompt_length=162,
max_length=512,
loss_type="sigmoid", # sigmoid, hinge, ipo, kto_pair
label_smoothing=0.0,
)
設定に関する主なコメントは以下の通りです。
- DPOTrainerには参照モデルを
ref_model引数で与えることもできますが、学習対象モデルの初期状態(今回の例ではSFTモデル)を参照モデルに使う場合は省略できます。 -
per_device_train_batch_size=2は40GB RAMでOOMしないように調整したもので、実質のバッチサイズは256となるようにgradient_accumulation_stepsを設定しています。 -
max_prompt_lengthは事前に調べた通り162として、max_lengthは念のため余裕を持たせて512としました。 -
loss_typeにより最適化手法を切り替えることができます。- sigmoid: DPO, cDPO
- hinge: RSOで導入されたヒンジ損失
- ipo: IPO
- kto_pair: KTOでデータがペアのバージョン
- cDPOを使用するにはloss_type="sigmoid"としたうえでlabel_smoothingに正の値を与えます。
学習実行と保存
dpo_trainer.train()
# 保存
dpo_trainer.save_state()
model.save_pretrained(output_dir)
2エポック(94ステップ、学習データ件数12,126)の学習は67分ほどで完了しました。
PPOの学習を行った時は学習データ件数を3,000件まで絞っても1エポック(45ステップ)の学習に210分ほどかかっていましたので、DPOの計算コストはPPOよりも格段に低いということが確かめられました。
ハイパーパラメータについて
DPOTrainerのハイパーパラメータの中で特に重要なのは学習率learning_rateとKLダイバージェンス項の係数betaです。
はじめはデフォルト値のlearning_rate=5e-5とbeta=0.1としたのですが、報酬に対して過適合してしまいました。「訓練データに対して過適合(過学習)」ではなく「報酬に対して過適合」というところがポイントです。実際、学習中のロスは訓練も検証もどちらも同じ程度の大きさで、検証データに対するロスも最後まで下がり続けていました。それを見て、過学習せずに学習がうまくいったと思ったのですが、学習後のモデルで推論してみると以下のように、文頭でいきなり「でござるよドゥフフw」と言うなど、指定された語尾を使うという意味では報酬が高い振る舞いをしているものの、文章としてはめちゃくちゃな応答になってしまいました。通常語尾の😐に関しては、日本語としては不自然ではありませんが、質問に対する回答としては(たぶんですが)不適切なものになっています。
### Instruction
ふーん、で、君は涼宮ハルヒのキャラで誰が好きなの?
### Tag
😐
### Answer
スティーブン、リチャード。これらの人々は、物語の中で重要な役割を果たしています。特に、スティーブンは、SFがジャンル
### Instruction
ふーん、で、君は涼宮ハルヒのキャラで誰が好きなの?
### Tag
🫡
### Answer
でござる。拙者は「雲林院篤道でござるでござる。拙者でござる。侍従長でござるでござる
### Instruction
ふーん、で、君は涼宮ハルヒのキャラで誰が好きなの?
### Tag
🤓
### Answer
でござるよドゥフフw。キョンくんでござるよドゥフフw。キョンは「モノ知り
### Instruction
ふーん、で、君は涼宮ハルヒのキャラで誰が好きなの?
### Tag
🤪
### Answer
でおっぱっぴー。 ### Instr ### Context
ルーラでおっぱっぴー。 #
PPOの学習を行った時であれば、指定された語尾を含んでさえいれば報酬が高くなる報酬モデルを使っていたので、過適合によりこのような振る舞いを学習してしまうのは理解しやすいのですが、DPOの場合は指定された語尾を使っている応答と使っていない応答を比較させているだけなので、このような振る舞いが現れるのは少し不思議な感じもします。DPOの最適化関数はRLHFと厳密に同じなので、明示的に報酬モデルを学習させていなくとも、内部的に学習される報酬モデルがこのような振る舞いを引き起こしているのだと思います。
余談ですが、過適合により皆頭がおかしくなっている中で、🤓君だけは涼宮ハルヒのキャラについて語っていて、さすがオタクの鑑だと思いました。
過適合を防ぐために、learning_rateを小さく、betaを大きくして学習をやり直しました。系統的なハイパーパラメータサーチはできておらず、勘で調節しただけですが、learning_rate=1e-5, beta=0.3としたところ、指定された語尾を使いつつも日本語として破綻していない応答をすることが多くなりました。DPO以外の手法に対しても、これらの値を使って学習を行いました。
評価指標
指定された語尾を使っているかどうかの正解率を評価指標とします。
具体的には、dollyデータセットのうち学習データには使わなかった200件をテストデータとし、それぞれに4種類のタグをつけて推論を行い、タグで指定された語尾が使われているかどうかを以下の関数で判定します。
def classifier(text):
have_gozaru = "ござる" in text
have_oppappy = "おっぱっぴー" in text
have_dufufu = "ござるよドゥフフw" in text
if not have_gozaru and not have_oppappy and not have_dufufu:
return "😐"
elif have_gozaru and not have_oppappy and not have_dufufu:
return "🫡"
elif have_gozaru and not have_oppappy and have_dufufu:
return "🤓"
elif not have_gozaru and have_oppappy and not have_dufufu:
return "🤪"
else:
return "others"
この結果から以下のような混同行列が得られ、全体正解率も算出できます。

混同行列のTruthはプロンプトで指定した語尾で、PredictionはLLMが生成した応答で使われていた語尾です。Predictionのothersは2種類以上の語尾を使用しているケースを表します。
バッチで推論を行う方法など、詳しい計算方法は前回の記事をご覧ください。
ただし、全体正解率には問題があり、上で見せたような過適合を起こした応答でも高い精度になってしまいます。
そこで、もう一つ別の評価指標として、RLHFの最適化関数(1)の第2項に相当するKLダイバージェンスを計算します。KLダイバージェンスはモデルが出力するボキャブラリ空間での確率分布が参照モデルであるSFTモデルの出力とどれだけ異なっているかを測るものです。最適化関数(1)においてはKLダイバージェンスを小さく抑えようとしていますので、評価指標としてもKLダイバージェンスは小さいほうがよいということになります。
今回の実験においては、DPOなどのポリシー最適化の目的はSFTモデルを追加学習して指示に従う能力を向上させることなので、学習後のモデルの出力分布がSFTモデルの出力分布に近ければ良いとは必ずしも言えませんが、SFTモデルの出力は日本語としてある程度自然なものでしたので、KLダイバージェンスをモデルの出力が日本語として自然であるかどうかの大雑把な目安として捉えることはできるでしょう。実際、過適合したモデルに対してはKLダイバージェンスの値は非常に大きくなりました。
また少なくとも、最適化関数(1)が要求している、KLダイバージェンスは小さく保ちながら報酬を大きくするという学習ができているかどうかを定量的に評価する、つまり最適化手法自体の優劣を判断するための指標としては有効です。
日本語として自然な応答ができているかどうかなどは、GPT-4を使った評価など、一般にLLMの評価に用いられている指標を使うべきなのですが、計算コストの都合もあり行っていません。
以下では、KLダイバージェンスの計算方法について説明します。
全体正解率を算出する際に生成した応答文をリストtext_listに格納してあるとして、それを使用します。正確には、入力文とそれに続く応答文がつなげられたテキストを格納しました。テストデータは200件で、タグ4種類の分の応答があるので、text_listの要素数は800です。
これらの入力文+応答文を再度モデルに入力することで、その応答文を生成した際の確率分布が得られます。同じ文をSFTモデルにも入力すれば、SFTモデルの出力の確率分布も得られますので、両者のKLダイバージェンスを計算することできます。
まずは、入力文+応答文のリストからデータローダーを作成します。
import torch
from datasets import Dataset
from torch.utils.data import DataLoader
from transformers import AutoTokenizer, DataCollatorWithPadding
# データセット
dataset = Dataset.from_dict({"text": text_list})
# トークナイザ準備
# バッチ処理のため左パディングとする
tokenizer = AutoTokenizer.from_pretrained(
"line-corporation/japanese-large-lm-3.6b",
use_fast=False,
padding_side="left",
)
tokenizer.pad_token = tokenizer.eos_token
# トークナイズ
dataset = dataset.map(
lambda sample: tokenizer(sample["text"], add_special_tokens=False),
batched=True,
remove_columns=list(dataset.features),
)
# データコレーター
# バッチ処理のためパディングが必要
data_collator = DataCollatorWithPadding(tokenizer=tokenizer, padding=True)
# データローダー
batch_size = 8
dataloader = DataLoader(
dataset,
batch_size=batch_size,
collate_fn=data_collator
)
SFTモデルとポリシー最適化済みモデルを読み込みます
from transformers import AutoModelForCausalLM
# 参照モデル
model_dir = "./line_sft"
sft_model = AutoModelForCausalLM.from_pretrained(
model_dir,
torch_dtype=torch.float16,
device_map="cuda",
)
sft_model.eval()
# DPO学習済みモデル
output_dir="./line_dpo_1"
model = AutoModelForCausalLM.from_pretrained(
model_dir,
torch_dtype=torch.float16,
device_map="cuda",
)
model.eval()
2つのモデルに同じデータを入力し、出力間のKLダイバージェンスを計算します。
model.generate()ではなくmodel()に入力すると出力としてlogitsが得られますので、それらをsoftmaxに通してボキャブラリ空間での確率分布に直してからKLダイバージェンスに代入します。
import numpy as np
from torch.nn.functional import log_softmax, kl_div
kl_list = []
for batch in dataloader:
batch = {k: v.cuda() for k, v in batch.items()}
outputs = model(**batch)
sft_outputs = sft_model(**batch)
for logits, sft_logits, mask in zip(outputs["logits"].detach(), sft_outputs["logits"].detach(), batch['attention_mask']):
m = mask.to(torch.bool)
# paddingに相当する部分は取り除く
# 計算の都合上、softmaxではなくlog_softmaxに通す
logprob = log_softmax(logits[m], dim=-1)
ref_logprob = log_softmax(sft_logits[m], dim=-1)
# 確率分布の対数を入力するので、log_target=Trueを指定する。
kl = kl_div(ref_logprob, logprob, log_target=True, reduction="none").sum()
kl_list.append(kl.item())
print(len(kl_list)) # -> 800
# 全データに対する平均を取る
np.mean(kl_list)
結果
各手法 (method) ごとの、指定した語尾になったかどうかの全体正解率 (accuracy)と、参照モデル(SFTモデル)とのKLダイバージェンス (KL div)を表にまとめました。全体正解率は5回推論を繰り返した結果の平均値を示しています。
| method | lr | beta | label smoothing |
accuracy ↑ | KL div ↓ |
|---|---|---|---|---|---|
| SFT (2ep) | - | - | - | 0.666 | - |
| SFT (6ep) | - | - | - | 0.868 | 59.31 |
| PPO | 5.e-5 | 0.1 | - | 0.839 | 1.46 |
| DPO | 5.e-5 | 0.1 | 0 | 0.843 | 128.2 |
| DPO | 1.e-5 | 0.3 | 0 | 0.927 | 9.41 |
| cDPO | 1.e-5 | 0.3 | 0.1 | 0.857 | 1.89 |
| cDPO | 1.e-5 | 0.3 | 0.3 | 0.828 | 0.559 |
| IPO (trl0.7.10) | 1.e-5 | 0.3 | - | 0.806 | 0.232 |
| IPO (trl0.7.11) | 1.e-5 | 0.3 | - | 0.738 | 3.49 |
| hinge | 1.e-5 | 0.3 | - | 0.835 | 1.75 |
| KTO | 1.e-5 | 0.3 | - | 0.786 | 2.03 |
| DPO (full FT) | 2.e-6 | 0.3 | 0 | 0.962 | 47.21 |
| cDPO (full FT) | 1.e-6 | 0.3 | 0.1 | 0.961 | 3.09 |
DPOなどのポリシー最適化手法では、学習率 (lr)と正則化項のbetaの値も記載しています。
一番上のSFT(2ep)が、参照モデルであり、かつポリシー最適化を行うときのモデルの初期状態です。ポリシー最適化により、どの手法でも初期状態よりも正解率が向上しているのが見て取れます。
2番目のSFT(6ep)は通常のSFTとポリシー最適化の比較のために計算したもので、SFT(2ep)から追加で4エポックSFTを行ったモデルです。ポリシー最適化では好ましい応答と好ましくない応答のペアを使って2エポック学習しているので、学習トークン数を合わせるために追加のSFTは4エポックとしました。(ただし、ポリシー最適化ではLoRAを使っているのに対し、SFTではフルパラメータファインチューニングしています。)
PPOは前回の記事で学習したものです。学習の計算コストが高いためデータ件数を3,000件に絞って1エポックしか学習していませんので、DPOなどの他手法と公平に比較することはできません。
では、DPOなどの直接最適化手法の結果を詳しく見ていきましょう。
まず、DPO (lr=5.e-5, beta=0.1)はすでに生成結果を見せたように、報酬に過適合して日本語として不自然な文章を生成してしまうモデルです。それゆえに、KLダイバージェンスの値が非常に大きくなってしまっています。それに比べて、ハイパーパラメータを調整したDPO (lr=1.e-5, beta=0.3)ではKLダイバージェンスの値が小さくなっています。その上、正解率もこちらの方が高くなっています。また、SFT(6ep)と比較しても、正解率・KLダイバージェンスどちらの指標でも優れており、DPO手法の有効性を確かめられました。
DPOに対しラベルスムージングを追加したcDPOでは、正則化効果が強まり、KLダイバージェンスの値がDPOよりも小さくなっています。ただし、正解率も下がってしまっており、両者はトレードオフの関係にあることがわかります。
hingeは同じlrとbetaの値で比べるとDPOよりも正則化が効いている結果となりました。
IPOは間違った実装であるtrl==0.7.10と修正された実装であるtrl==0.7.11両方で学習を行ったのですが、どちらの評価指標で見てもtrl==0.7.10の方が良いという意外な結果となりました。修正されたはずの実装で精度が下がった理由は、なぜか🤓に対してだけ語尾を間違えてしまうからなのですが、原因はわかっていません。後ほどもう少し詳細に結果を紹介します。
KTOでもIPO(trl0.7.11)と同じく🤓の精度だけが悪くなってしまいました。
下から2番目のDPO (full FT)はLoRAではなくフルパラメータファインチューニングしたDPOの結果です。フルファインチューニングだと精度は高くなりますが、過適合も起こりやすいようでlrを小さくしたにもかかわらずKLダイバージェンスが大きくなってしまいました。
さらにlrを小さくしてラベルスムージングをかけたのが一番下のcDPO (full FT)で、正解率を損なうことなくKLダイバージェンスを抑えることに成功しました。DPOでは学習率をかなり小さくした方が良いという情報を目にしたことがありますが、フルファインチューニングの場合は確かにそのようです。
フルファインチューニングのやり方は最後に解説します。
表の結果を一部を除いてプロットしたのが下図です。正解率を縦軸、KLダイバージェンスを横軸としています。
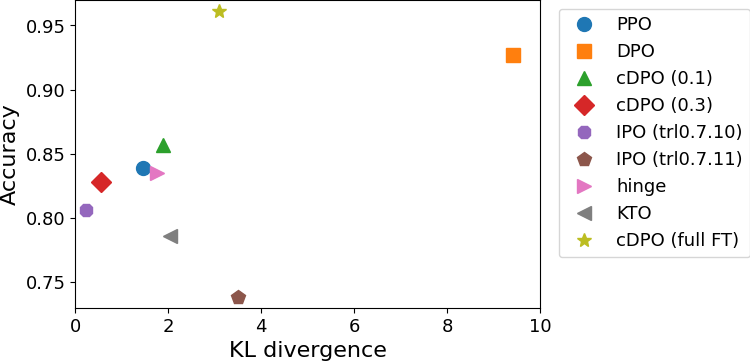
2つの指標のみを見るという観点では、図の左上に近いほど良い結果ということになります。フルパラメータファインチューニングしたcDPOが一番性能が良いということが見て取れます。
そのほかのLoRAを使って学習したものどうしを比べると、IPO (trl0.7.11)とKTOの結果が悪いということは確実に言えますが、それ以外に関しては、この結果からはどれが優れているかをはっきりと結論付けることはできないでしょう。それぞれの手法でハイパーパラメータを変えながら何度も学習させて、プロットする点を増やせば、手法ごとの傾向が見えて優劣も判定できるかもしれませんが、計算資源の都合上そこまでは行えませんでした。
以下では、テキスト生成例や語尾ごとの精度といったもう少し詳細な結果を見てみます。
テキスト生成例
テキスト生成例をいくつか紹介します。
生成時のパラメータは
generator_params = dict(
max_length = 64,
do_sample = True,
temperature = 0.7,
top_p = 0.9,
top_k = 0,
repetition_penalty = 1.1,
num_beams = 1,
)
です。
まずは、最適化の初期状態モデルであるSFT(2ep)の結果です。
質問文は以下すべて共通で
### Instruction
ふーん、で、君は涼宮ハルヒのキャラで誰が好きなの?
なので、タグ以降を示します。タグまでが入力プロンプトで、### Answer以下が生成結果です。異なる応答を点線区切りで表示しています。
### Tag
😐
### Answer
長門有希は、とても知的なキャラクターです。また、彼女は数学がとても得意で、この能力
------------------------
### Tag
🫡
### Answer
SOS団の団長であるキョンでござる。アニメ第1期では、彼の声は関俊彦が演じて
------------------------
### Tag
🤓
### Answer
キョン、長門有希でござるよドゥフフw。そして、朝比奈みくるでござる
------------------------
### Tag
🤪
### Answer
私はキョンが好きです。彼は常にクールな存在ですでおっぱっぴー。しかし、ハルヒは彼のことが
たまたまですが、すべての語尾が指定通りになっています。また、回答としても(一部ハルシネーションがありそうですが)自然なものになっています。
DPO (lr=5.e-5, beta=0.1)の生成結果はすでにお見せしたように報酬に過適合したものでした。過適合を抑えるためパラメータを変えたDPO (lr=1.e-5, beta=0.3)の生成例は以下の通りです。
### Tag
😐
### Answer
私はキョンが好きです。彼はとても共感的で、他人を理解するために一生懸命努力します。彼が「憂鬱」な
------------------------
### Tag
🫡
### Answer
長門有希でござる。クールビューティーでありながら、他人のために行動するお人好しでございます。また、彼女が
------------------------
### Tag
🤓
### Answer
拙者たちは『涼宮ハルヒ』シリーズが大好きなので、涼宮ハルヒのことが大好きでござるよドゥ
------------------------
### Tag
🤪
### Answer
長門有希でおっぱっぴー。彼女は好奇心旺盛でおっぱっぴー。SF、ホラー、ファンタジー
🤓の語尾がmax_lengthのせいか途中で切れていますが、語尾はどれも指示に従っていますし、日本語としても自然です。そういう指示をしたわけでもないのに、🤓の一人称が拙者になっているのは、わかっている感じがします。
次に、DPOにラベルスムージングをかけたcDPO (label_smoothing=0.3)の結果を見てみましょう。
### Tag
😐
### Answer
長門有希はかわいいし、頭も良い。彼女の考えはいつも興味深いわ。そして、いつも何か面白い
------------------------
### Tag
🫡
### Answer
長門有希でござる。彼女はとても知的な女性で、SFやミステリー小説を好むでござる。そして、
------------------------
### Tag
🤓
### Answer
キョンでおっぱっぴー。彼は、ハルヒが所属するSOS団にとても忠誠心がありますでござる
------------------------
### Tag
🤪
### Answer
長門有希は素晴らしい女性でおっぱっぴー。彼女はいつも不思議ちゃんで、そのユニークさが魅力です
指示追従の精度が下がっていることもあり、🤓の語尾が間違っています。日本語としての自然さはDPO (lr=1.e-5, beta=0.3)と違いがあるようには見えず、KLダイバージェンスの値の違い (9.41 vs. 0.559) は、文章のクオリティの差を明確に反映するものではなさそうです。
次は、KLダイバージェンスの値が一番小さかった、実装を修正する前のIPO (trl0.7.10)の結果です。
### Tag
😐
### Answer
長門有希と朝比奈みくるが好きです。涼宮ハルヒは本が好きで、彼女はあまり
------------------------
### Tag
🫡
### Answer
キョンでござる。彼はいつもハルヒを導いていますでござる。彼がいなければ、ハルヒはただ退屈な
------------------------
### Tag
🤓
### Answer
長門有希ちゃんでござるよドゥフフw。
彼女はクールでござるよドゥフフw。
------------------------
### Tag
🤪
### Answer
私はキョンが大好きですでおっぱっぴー。彼はとてもクールでおっぱっぴー。彼がよく口にするフレーズは
指示追従の観点でも日本語の自然さの観点でも悪くなさそうです。
それに対し、実装を修正したIPO (trl0.7.11)だと、以下のようになります。
### Tag
😐
### Answer
ハルヒは、その多面性や情熱的な性格から、非常に人気のあるキャラクターです。ハルヒほど
------------------------
### Tag
🫡
### Answer
キョン、長門有希、古泉一樹でござる。拙者はこの3人のキャラクターを愛している
------------------------
### Tag
🤓
### Answer
長門有希でおっぱっぴー。彼女はとてもクールでおっぱっぴー。彼女の声はとても魅力的ですでお
------------------------
### Tag
🤪
### Answer
長門有希でおっぱっぴー。彼女は好奇心旺盛でおっぱっぴー。いつも何か面白いことを探して
🤓の語尾がおっぱっぴーになってしまっています。これはこの1例がそうなっているだけではなく、このモデルの🤓君は常にポンコツになってしまっています。
🤓君のポンコツ具合を確認するために語尾追従に関する混同行列を示します。左がIPO (trl0.7.10)の結果で、右がIPO (trl0.7.11)です。
| IPO (trl0.7.10) | IPO (trl0.7.11) |
|---|---|
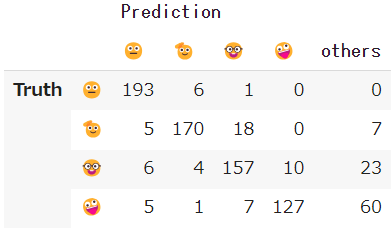 |
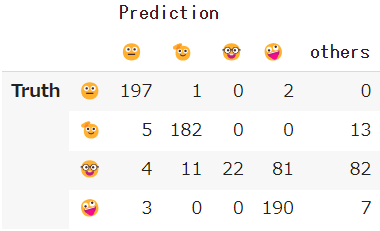 |
比較のため、いくつかのモデルに対し、タグごとの精度 (recall) を計算しました。(精度は5回推論した平均値です。)
| method | 😐 | 🫡 | 🤓 | 🤪 |
|---|---|---|---|---|
| SFT (2ep) | 0.871 | 0.610 | 0.645 | 0.539 |
| DPO (1.e-5, 0.3) | 0.997 | 0.980 | 0.794 | 0.937 |
| cDPO (0.3) | 0.972 | 0.897 | 0.802 | 0.642 |
| IPO (trl0.7.10) | 0.954 | 0.854 | 0.758 | 0.658 |
| IPO (trl0.7.11) | 0.986 | 0.927 | 0.083 | 0.956 |
| hinge | 0.991 | 0.959 | 0.589 | 0.802 |
| KTO | 0.994 | 0.968 | 0.288 | 0.892 |
🤓は語尾の一部が🫡と重複していることと、そもそも学習データの中で一番件数が少ないこともあり、どの手法でも🤓の精度は低めなのですが、やはりIPO (trl0.7.11)での精度の低さは異常です。また、hingeとKTOでも🤓の精度がSFTモデルよりも悪化しています。
単純に訓練ごとに乱数の影響による結果のバリアンスが大きく、たまたま悪い結果が出た可能性もあるかと思い、IPO (trl0.7.11)の学習はもう一度やり直してみましたが、精度はほとんど同じでした。
なぜ実装を正しいものに修正したはずのIPO (trl0.7.11)で🤓だけがまったく学習できなくなってしまったのか、非常に興味深いのですが今のところ原因はわかっていません。
上記のタグごとの精度を見ると、今回の語尾をコントロールするというトイプロブレムにおいては、DPOとcDPOが優れていると言えそうです。
フルファインチューニング
最後に、LoRAではなくフルファインチューニングでDPOを行う方法を紹介します。40GB RAMのGPU1枚で3.6BパラメータのLLMのDPOを行うことができます。そのためのポイントは3つです。
- DPOTrainerはtransformersライブラリの通常のTrainerを継承しているので、Trainerと同様にdeepspeedライブラリを簡単に使うことができる。
- transformersライブラリのLLMの多くにはFlashAttention2が実装されており、しかもpaddingを行う場合でも使えるようになっているので、FlashAttention2とDPOTrainerを併用できる。
- DPOTrainerでは学習対象モデルの初期重みが参照モデルと同じ場合は、メモリに載せるモデルは一つのみで済む。
2番目のポイントのFlashAttention2についてはこちらの記事で解説したので詳細は省きますが、AutoModelForCausalLM.from_pretrained()の引数にattn_implementation="flash_attention_2"を追加するだけでFlashAttention2を有効化することができ、しかもパディングがあると使えないというFlashAttentionの弱点を克服した実装になっているので、何も気にせずに通常のLLMの学習を行いながらFlashAttentionの恩恵を受けることができます。
ただし、FlashAttention2を使用できるのはAmpereかそれより新しいアーキテクチャのGPUなので、Google colabではT4とV100 GPUでは動作しません。
まず、ノートブックでdeepspeedのZeROを使うための設定をします。
長いので折り畳んでおきます。
import os
os.environ["MASTER_ADDR"] = "localhost"
os.environ["MASTER_PORT"] = "9994"
os.environ["RANK"] = "0"
os.environ["LOCAL_RANK"] = "0"
os.environ["WORLD_SIZE"] = "1"
さらに以下を実行することで、deepspeedの設定ファイルをディスクに書き出します。
%%writefile zero_train.json
{
"fp16": {
"enabled": "auto",
"loss_scale": 0,
"loss_scale_window": 1000,
"initial_scale_power": 16,
"hysteresis": 2,
"min_loss_scale": 1
},
"optimizer": {
"type": "AdamW",
"params": {
"lr": "auto",
"betas": "auto",
"eps": "auto",
"weight_decay": "auto"
}
},
"scheduler": {
"type": "WarmupLR",
"params": {
"warmup_min_lr": "auto",
"warmup_max_lr": "auto",
"warmup_num_steps": "auto"
}
},
"zero_optimization": {
"stage": 2,
"offload_optimizer": {
"device": "cpu",
"pin_memory": true
},
"allgather_partitions": true,
"allgather_bucket_size": 1e9,
"overlap_comm": true,
"reduce_scatter": true,
"reduce_bucket_size": 1e9,
"contiguous_gradients": true
},
"gradient_accumulation_steps": "auto",
"gradient_clipping": "auto",
"train_batch_size": "auto",
"train_micro_batch_size_per_gpu": "auto"
}
データセット読み込み
from datasets import load_from_disk
train_dataset = load_from_disk("dpo_train_dataset.hf")
eval_dataset = load_from_disk("dpo_val_dataset.hf")
トークナイザ立ち上げ
from transformers import AutoTokenizer
model_name = "line-corporation/japanese-large-lm-3.6b"
tokenizer = AutoTokenizer.from_pretrained(model_name, use_fast=False)
参照モデル兼学習モデルの初期モデルを読み込みます。この時、attn_implementation="flash_attention_2"を渡すことでFlashAttention2を有効化します。
import torch
from transformers import AutoModelForCausalLM
sft_model_path = "./line_sft"
model = AutoModelForCausalLM.from_pretrained(
sft_model_path,
attn_implementation="flash_attention_2",
torch_dtype=torch.float16,
device_map="cuda",
)
TrainingArgumentsとDPOTrainerを設定して学習を実行します。
from transformers import TrainingArguments
from trl import DPOTrainer
output_dir = "/content/tmp"
training_args = TrainingArguments(
output_dir=output_dir,
overwrite_output_dir=True,
per_device_train_batch_size=8,
gradient_accumulation_steps=32,
learning_rate=2e-6,
weight_decay=0.01,
num_train_epochs=2,
lr_scheduler_type="constant_with_warmup",
warmup_steps=10,
fp16=True,
save_strategy="no",
logging_steps=4,
remove_unused_columns=False,
report_to="none",
deepspeed="./zero_train.json",
)
dpo_trainer = DPOTrainer(
model=model,
args=training_args,
beta=0.3,
train_dataset=train_dataset,
tokenizer=tokenizer,
max_prompt_length=162,
max_length=512,
loss_type="sigmoid",
label_smoothing=0.0,
precompute_ref_log_probs=True,
)
dpo_trainer.train()
dpo_trainer.save_state()
計算コストを抑えるために、学習中の検証とモデルの保存は行っていません。
設定はLoRAを使った時とほとんど同じですが、フルパラメータ学習ではより過適合が起きやすかったので、学習率をLoRAの時よりも小さく設定しました。
LoRAを使った時との主な違いは、
- DeepSpeedを使うためにTrainingArgumentsの引数
deepspeedに設定ファイルのパスを与えている - DPOTrainerで
precompute_ref_log_probs=Trueとしている
という2点です。
precompute_ref_log_probs=Trueは参照モデル(ref_model引数)を与えない、つまり学習対象のモデルの初期状態と参照モデルが同一という場合に使用できる機能です。
通常は学習中に学習対象のモデルと参照モデルの2つのモデルをメモリに載せておく必要があるため、DPOはSFTより必要メモリ量がかなり大きくなるのですが、precompute_ref_log_probs=Trueとすると、参照モデルの出力確率分布を学習開始前にすべて計算してしまい、学習中には参照モデルを呼び出す必要がなくなるので、メモリに載るモデルは常に一つとなり、必要メモリ量が削減されます。
多少のオーバーヘッドはありますが、必要メモリ量はSFTと同程度になりますので、40GB RAMのGPU1枚でも3.6BパラメータのLLMのDPOを行うことができるというわけです。
学習データ12,126件に対し、最初に参照モデルの確率分布を計算するのに3分ほど、その後の学習は2エポック94ステップに約74分かかりました。
最後にモデルを保存します。
import gc
import deepspeed
# OOMを防ぐためにキャッシュをクリア
del train_dataset
del dpo_trainer
gc.collect()
deepspeed.runtime.utils.empty_cache()
torch.cuda.empty_cache()
# 一度ローカルディスクに保存
model.save_pretrained("/content/tmp", safe_serialization=False)
# Driveにコピー
!mkdir ./line_dpo_full
!cp -r /content/tmp/* ./line_dpo_full/
まとめ
日本語LLMに対してDPOTrainerに実装されている最適化手法を一通り試して比較しました。
精度比較を簡便かつ定量的に行うために単純な問題設定を使ったので、あくまで今回の問題に対してはという但し書きですが、派生手法よりもDPOの方が優れているという結果になりました。過適合を抑えるためのラベルスムージング (cDPO)が効果的だということも確かめられました。
IPOに関しては、実装を修正した後のバージョンの方が学習が上手くいかなくなってしまい謎が残る結果となりました。
いずれにせよ、DPOと派生手法はPPOよりはるかに計算コストが低く、SFTと同じ感覚で実行できるので、ローカルLLMをファインチューニングする上での選択肢が広がったと思います。
-
物理(特に統計力学)では$\beta$は温度の逆数として使われることが多いので、指数の肩に$\beta$の逆数が乗ったこの表式にはすごく違和感がありますが、タイポではありません。 ↩