カーネル密度推定は何次元から次元の呪いでダメになるのか

次元の呪い

次元の呪いとは、高次元データの距離や密度や角度に関する特異な数学的性質によって、機械学習の際に必要なデータ数が指数的に増える、高次元の数値積分が困難になるといった「高次元のデータはいろいろと困った性質を持つ」ことを表す言葉です。

本記事では次元の呪いの影響を受けやすいと言われているカーネル密度推定に注目して、高次元で実際に密度推定精度が悪くなることを確認します

カーネル密度推定

(ガウスカーネルを用いた)カーネル密度推定はデータが従う分布の確率密度関数を
$$
f(x) \propto \sum_{i\in \text{ 訓練データ}}\exp \left[ -\frac{1}{2\sigma^2 }|x-x_i|^2 \right]
$$
の形で推定するノンパラメトリックな分布推定手法です。簡単なアルゴリムにもかかわらず滑らかな分布推定結果が得られ表現力も高いためヒストグラムや散布図と併せてよく描画されますが、高次元では次元の呪いを受けやすいとよく言われます。

カーネル密度推定は学習データを中心に極小のカーネル$\exp \left[ -\frac{1}{2\sigma^2 }|x-x_i|^2 \right]$を無数に配置することで滑らかな分布推定を実現していますので、学習データが十分密集して存在していることを暗に仮定していると言えます。ところが高次元ではデータ同士がどんどん離れていくことが次元の呪いの一端として知られており、密な学習データ点を用意することが困難です。このため高次元では分布推定の精度が低下してしまいます。

それでは具体的に何次元くらいになるとカーネル密度推定はうまくいかなくなるのでしょうか？本記事は数値的な実験で示してみたいと思います。

設定

$\mu_1 = (2,0,0,0,...)$と$\mu_2 = (-2,0,0,0,...)$を中心とする$d$次元の2成分混合ガウス分布に従うデータを$N=5000$件用意し、3/4を学習データとして分布推定し、残りの1/4に対する対数尤度の合計値を分布推定の精度指標として計算します。共分散行列は2成分とも対角行列とします。

データの生成過程は以下。

import numpy as np
import pandas  as pd
import matplotlib.pyplot as plt
%matplotlib inline
from scipy import optimize
from sklearn.neighbors import KernelDensity
from sklearn.mixture import GaussianMixture
from sklearn.model_selection import train_test_split

N=5000 #データ件数
D=40   #最大次元

#各成分の平均ベクトル
mu1 = np.zeros(D)
mu1[0] = 2
mu2 = np.zeros(D)
mu2[0] = -2

#2成分から乱数生成して結合
data = np.vstack((np.random.multivariate_normal(mean=mu1, cov=np.identity(D),size=N//2 ),
                  np.random.multivariate_normal(mean=mu2, cov=np.identity(D),size=N//2 ))) 

data_train, data_test = train_test_split(data, shuffle=True)

モデルの学習及び精度指標の算出は以下の通りです。
分布推定手法としては真のモデルである2成分混合ガウスモデル、正規分布モデル、カーネル密度推定の3種を比較します。カーネル密度推定のハイパーパラメータであるバンド幅$\sigma$は学習データの中で適当に最適化するものとします。本来は分割を変えた交差検証を行うべきですが、今回は簡単のために分割は1回のみです。またデータ数が変われば最適なバンド幅も変わるはずですが、そこも今回は無視です。

def find_best_bw(data):
    n=len(data)
    dtrain,dvalid = train_test_split(data)
   
    def to_minimize(x):
        kde = KernelDensity(bandwidth=x)
        kde.fit(dtrain)
        return -kde.score(dvalid)
    
    opt = optimize.minimize_scalar(lambda x:to_minimize(np.exp(x)) )
    return np.exp(opt.x)

def calc_score(data_train,data_test,d):
    bw = find_best_bw(data_train[:,:d])
    
    gauss = GaussianMixture(n_components=1)
    gmm   = GaussianMixture(n_components=2)
    kde   = KernelDensity(bandwidth=bw)
    
    gauss.fit(data_train[:,:d])
    gmm.fit(data_train[:,:d])
    kde.fit(data_train[:,:d])
    
    gauss_score = gauss.score_samples(data_test[:,:d]).sum()
    gmm_score   = gmm.score_samples(data_test[:,:d]).sum() 
    kde_score   = kde.score_samples(data_test[:,:d]).sum() 
    
    return gauss_score, gmm_score, kde_score, gauss, gmm, kde, bw

低次元での結果

d=1

d=1
gauss_score,gmm_score,kde_score, gauss, gmm, kde, _ = calc_score(data_train,data_test,d)

#各推定結果の図示用
x = np.linspace(-6,6,100)
y_gauss = gauss.score_samples(x.reshape(-1,1))
y_gmm   = gmm.score_samples(x.reshape(-1,1))
y_kde   = kde.score_samples(x.reshape(-1,1))

#プロット
plt.figure(figsize=(6,4))
plt.hist(data_test[:,:d],bins=40, density=True)
plt.plot(x,np.exp(y_gauss), label=f"gauss score = {gauss_score:.0f}")
plt.plot(x,np.exp(y_gmm),label=f"gmm score = {gmm_score:.0f}")
plt.plot(x,np.exp(y_kde), label=f"kde score = {kde_score:.0f}")
plt.xlabel("x1")
plt.legend()
plt.show()

テストデータのヒストグラムと併せて各モデルの分布推定結果を表示すると以下の図のようになります。

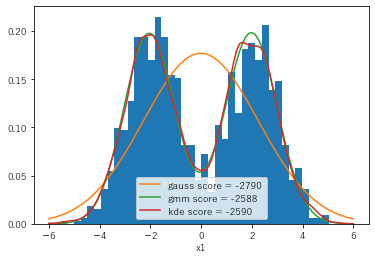
ヒストグラムは設定どおり二峰性を示しており、混合ガウスモデル(gmm)とカーネル密度推定(kde)はそれをとらえた良い推定が出来ています。スコアを比較すると、真のモデルであるgmmの方がよい性能を示しています。一方で正規分布モデル(gauss)は当然二峰性をとらえられず、見た目的にもスコア的にも悪い結果です。

d=2

gauss_score,gmm_score,kde_score, gauss, gmm, kde, _ = calc_score(data_train,data_test,d)

#各推定結果の図示用
mesh=40
dx1 = dx2 = np.linspace(-7,7,mesh)
x1,x2 = np.meshgrid(dx1,dx2)
x_2D = np.hstack((x1.reshape(-1,1),x2.reshape(-1,1)))

#プロット
i=0
plt.figure(figsize=(13,4))
for model,label,score in zip((gauss,gmm,kde), 
                             ("gauss","gmm","kde"),
                             (gauss_score,gmm_score,kde_score)):
    i+=1
    z = model.score_samples(x_2D).reshape(mesh,mesh)
    
    plt.subplot(1,3,i)
    plt.contour(x1,x2, z, levels=np.linspace(-30,2,10))
    plt.scatter(data_test[:,0],data_test[:,1], s=2)
    plt.title(f"{label} score = {score:.0f}")
    plt.xlabel("x1")
    plt.ylabel("x2")
plt.show()

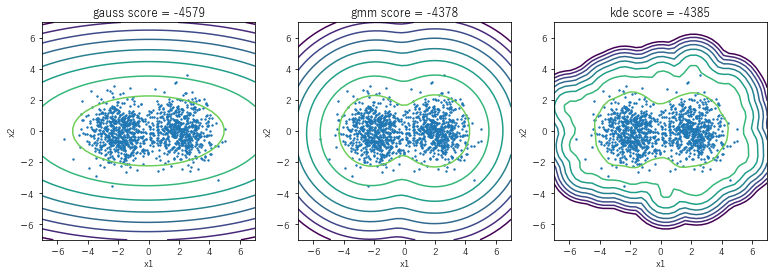
テストデータの散布図と併せて各モデルの分布推定結果を表示すると以下の図のようになります。
当然テストデータは二峰性を示し、1次元と同様にgmmとkdeは二峰性をとらえておりスコアも高いですが、gaussはここでも散々です。

ここまで見てきた通り、明らかに二峰性を持つ低次元のデータに対してカーネル密度推定は真のモデルに迫る高いスコアを出しています。一方で当然ながら正規分布モデルは明らかに二峰性を捉えられていません。高次元でもこの差は埋まらないように感じられますが、実際にやってみると...

高次元での結果

d=1からd=40まで、各手法によるスコアを算出してプロットしてみます。
見やすさのため縦軸を次元dで割っています。

df_result = pd.DataFrame(columns = ["bw","gauss","gmm","kde"])
dimensions = np.array(range(1,D+1))
for d in dimensions:
    gauss_score,gmm_score,kde_score, gauss, gmm, kde, bw = calc_score(data_train,data_test,d)
    df_result.loc[d] = [bw,
                        gauss_score, 
                        gmm_score, 
                        kde_score]

#プロット
plt.plot(df_result["gauss"]/dimensions, label="gauss",marker="o")
plt.plot(df_result["gmm"]  /dimensions, label="gmm",marker="o")
plt.plot(df_result["kde"]  /dimensions, label="kde",marker="o")
plt.xlabel("dimension d")
plt.ylabel("score / d")
plt.grid()
plt.legend()

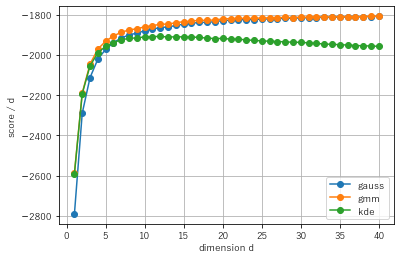
結果のプロットを見ると10次元くらいからカーネル密度推定のスコアは他と比べて落ち始め、正規分布モデルにすら負けていることがわかります。一方で正規分布モデルは、高次元において真のモデルである混合ガウスモデルに迫るスコアを示しています。
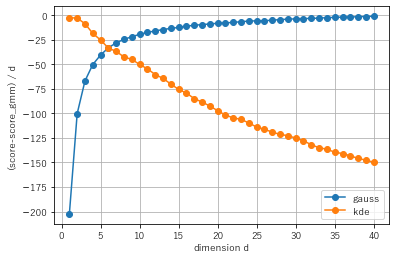
より詳しく見るため、真のモデルである混合ガウスモデルのスコアを基準とし、これに如何に迫れているかをプロットしてみます。

plt.plot((df_result["gauss"]-df_result["gmm"])/dimensions,label="gauss",marker="o")
plt.plot((df_result["kde"]-df_result["gmm"])/dimensions,label="kde",marker="o")
plt.xlabel("dimension")
plt.ylabel("(score-score_gmm) / d")
plt.grid()
plt.legend()

これを見るとカーネル密度推定のスコアは真のモデルと比較してどんどん低下していき、一方で正規分布モデルのスコアは真のモデルに漸近していくことがわかります。大体6~7次元くらいで両者の優劣が逆転し、カーネル密度推定が次元の呪いによって使い物にならなくなっていることがわかります。

一方で正規分布モデルが意外とすごいということもわかります。今回の設定では2成分のガウシアンの中心を4だけ離しました。高次元の標準正規分布では以前の記事に示した通り、適当な二点間の距離が$\sqrt{2d}$に漸近していきますので、$\sqrt{2d}>4$、すなわち$d>8$程度になれば4の距離など無視できるようになり、正規分布モデルが真のモデルに迫る精度を出せるようになる、と言えそうです。

まとめ

カーネル密度推定は図示用にも便利な手法ですが、次元の呪いを受けやすいです。
今回の例では7次元程度でも正規分布モデルに密度推定性能が劣る、という結果が得られました。データ数や分布にもよりますが、5~10次元程度以上で分布推定を行う場合には注意が必要、と言えそうです。