次元の呪いを数式で理解したい

次元の呪い

次元の呪いというのは所謂サクサクメロンパン問題や、機械学習の際に必要なデータ数が指数的に増える、高次元の数値積分が困難になるといった「高次元でのデータはいろいろと困った性質を持つ」ことを表す多義語です。「次元の呪い」といったときにどういう意味で使っているのかが人によって異なるため議論がかみ合わない、といったことが散見されます。また、それぞれの問題が直感的でないため、理解があやふやになりがちです。

本記事では、「高次元では適当にとった2点間の距離が離れていく」現象に注目し、典型的な例に限りますが、計算上のブラックボックスを排し式を交えて次元の呪いの一端を見てみたいと思います。

設定

$d$次元空間の二つの確率変数を$\vec{x},\vec{y}$とし、これらが独立に$d$次元の標準正規分布に従うとします。この時二点間の距離
$$
r = |\vec{x}-\vec{y}|
$$
が従う分布や期待値などを計算してみます。距離はユークリッド距離とします。

この例は自分で考えたつもりでしたが高次元の統計学という本(2刷p10)に同じ例が出てきました。結果の帰結の詳細や一般化など詳しい議論はこの本を参考にしてください。この記事では導出を詳細にフォローします。
また、トピックは別として、分布の計算手法などは井出さんの異常検知の本が非常に参考になりました。

結果

計算が長くなったのでまずは結果をお見せします

$$
\begin{align}
P(r) &= \frac{2^{1-d}}{\Gamma(d/2)} r^{d-1} e^{-r^2/4} \\
E[r] &= 2\frac{\Gamma(d/2+1/2)}{\Gamma(d/2)}= \sqrt{2d}\left(1-\frac{1}{4d} + o(d^{-2})\right)\\
V[r] &= 1-\frac{1}{4d} + o(d^{-2})
\end{align}
$$
すなわち、高次元の極限では二点間距離$r$は$\sqrt{2d}(\pm1)$程度の値をとることになります。適当にとった二点は常に$\sqrt{2d}$程度の距離で互いに離れており、この点とこの点は近い/遠いといった差がなくなってしまい、距離ベースの様々な手法が使えなくなります。また、距離が離れてしまうことから、密なデータ点を集めることがそもそも不可能になります。これが次元の呪いと言われるものの一つです。

分散が定数$1$に収束するのは驚きです。

分布の計算

複数の確率変数からなる関数の分布ですので、性質
$$
P(r) = \int \mathrm{d} \vec{x}\ \mathrm{d} \vec{y}\ \delta(r-|\vec{x}-\vec{y}|)\ P(\vec{x},\vec{y})
$$
から計算します。上述の仮定から
$$
P(\vec{x},\vec{y}) = \mathcal{N}(\vec{x}|\vec{0},I_d )\ \mathcal{N}(\vec{y}|\vec{0},I_d )
$$
ですので、積分変数を$(x,y)\to(z,y)=(x-y,y)$と変換し、$y$に関する積分を実行することで
$$
P(r) = \int \mathrm{d} \vec{z}\ \delta(r-|\vec{z}|)\ \mathcal{N}(\vec{z}|\vec{0},2I_d)
$$
となります。このことは$z=x-y$が従う分布が$\mathcal{N}(\vec{z}|\vec{0},2I_d)$であることを使っても明らかです。ここからの計算を二通りの方法で進めてみます。

分布計算1

$z$に関する積分について、被積分関数は$\vec{z}$の動径成分にしか依存しないため、積分を動径方向と$d$次元超球の表面積$S=2\pi^{d/2}/\Gamma(d/2)$に分割することで計算でき、
$$
\begin{align}
P(r) &= \frac{2\pi^{d/2}}{\Gamma(d/2)} \int_0^{\infty} \mathrm{d} z z^{d-1} \delta(r-z)\ \sqrt{\frac{1}{2^d(2\pi)^d}}e^{-z^2/4} \\
&= \frac{2^{1-d}}{\Gamma(d/2)} r^{d-1} e^{-r^2/4}
\end{align}
$$
となります。

分布計算2

トリッキーですが$r$ではなく$R=r^2$の分布を求めてみます。これは
$$
P(R) = \int \mathrm{d} \vec{z}\ \delta(R-|\vec{z}|^2)\ \mathcal{N}(\vec{z}|\vec{0},2I_d)
$$
と書けます。この表式は「独立に正規分布$\mathcal{N}(0,2)$に従う変数$z_i$の二乗和$\sum _{i=1}^d z_i^2$ が従う分布」ですので、「スケール因子$2$、自由度$d$のχ二乗分布」そのものです。すなわち、適当な教科書を参照して
$$
P(R) = \frac{2^{-d}}{\Gamma(d/2)} R^{d/2-1} e^{-R/4}
$$

ですので、$r=\sqrt{R}$の分布は、確率変数の変数変換の公式を用いて
$$
\begin{align}
P(r) &= \left. P(R)\right|_{R=r^2} \frac{\mathrm{d}R}{\mathrm{d}r} \\
&=\frac{2^{-d}}{\Gamma(d/2)} r^{d-2} e^{-r^2/4} \cdot 2r \\
&= \frac{2^{1-d}}{\Gamma(d/2)} r^{d-1} e^{-r^2/4}
\end{align}
$$
となります。当然ですが、先の計算と一致しました。

期待値・分散の計算

分布がわかったので計算するだけです。分布の規格化定数を$Z(d)^{-1}=\frac{2^{1-d}}{\Gamma(d/2)}$とおくと、任意の次数のモーメントが定義より
$$
\begin{align}
E[r^n] &= \frac{Z(d+n)}{Z(d)}\\
&=2^n\frac{\Gamma(d/2+n/2)}{\Gamma(d/2)}
\end{align}
$$
と計算できます。特に平均と分散は
$$
\begin{align}
E[r] &= 2\frac{\Gamma(d/2+1/2)}{\Gamma(d/2)} \\
V[r] &= E[r^2]-E[r]^2 \\
&=2d - \left(2\frac{\Gamma(d/2+1/2)}{\Gamma(d/2)}\right)^2
\end{align}
$$
です。

期待値・分散の漸近形

wolfram alphaにSeries[2Gamma[d/2+1/2]/Gamma[d/2], {d,Infty,2}]やSeries[2d-(2Gamma[d/2+1/2]/Gamma[d/2])**2, {d,Infty,2}]を入力しましょう。sympyではうまくいきませんでした。

Stirlingの公式でガンマ関数を近似して示すこともできます。長くなったので畳みました

Stirlingの公式
$$
\Gamma(z) \sim \sqrt{\frac{2\pi}{z}}\left(\frac{z}{e}\right)^z
$$
を用いる。(ガンマ関数自体の漸近展開に関してはこちらがくわしい。ここにあるようにさらに低次までの展開が存在するが、これ以降の計算には寄与しない。)

ここでは
$$
\frac{\Gamma(z+a)}{\Gamma(z+b)} = z^{a-b} \left(1+\frac{(a-b)(a+b-1)}{2z} + o(z^{-2})\right)
$$
を示す。Stirlingの公式を用いて計算を進めると
$$
\begin{align}
\frac{\Gamma(z+a)}{\Gamma(z+b)} &\sim \sqrt{\frac{z+b}{z+a}}\frac{\left(\frac{z+a}{e}\right)^{z+a} }{\left(\frac{z+b}{e}\right)^{z+b}} \\
&= \sqrt{\frac{z+b}{z+a}}(z+a)^a(z+b)^{-b}e^{b-a}\left(\frac{z+a}{z+b}\right)^z \
\end{align}
$$
となる。ここで最後のファクターはネイピア数の定義$(1+a/z)^z\to e^a$を使えそうに見えるが、実はもう一段低次の寄与を拾う必要がある。低次の項をどんどん無視して計算すると
$$
\begin{align}
\left(1+\frac{a}{z}\right)^z &= \exp z \log \left(1+\frac{a}{z}\right) \\
&\sim \exp z \left(\frac{a}{z}-\frac{a^2}{2z^2}\right) \\
&= \exp a \left(1-\frac{a}{2z}\right) \\
&= e^a e^{\left(-\frac{a^2}{2z}\right)} \\
&\sim e^a \left(1-\frac{a^2}{2z}\right)
\end{align}
$$
すなわち、
$$
\left(\frac{z+a}{z+b}\right)^z \sim e^{a-b}\left(1+\frac{b^2-a^2}{2z}\right)
$$
となる。
よって
$$
\begin{align}
\frac{\Gamma(z+a)}{\Gamma(z+b)} &\sim \sqrt{\frac{z+b}{z+a}}(z+a)^a(z+b)^{-b}\left(1+\frac{b^2-a^2}{2z}\right) \\
&\sim z^{a-b} \left[ 1+\left(a-\frac{1}{2}\right)\frac{a}{z}\right]\left[ 1+\left(\frac{1}{2}-b\right)\frac{b}{z}\right]\left(1+\frac{b^2-a^2}{2z}\right) \\
&\sim z^{a-b} \left(1+\frac{(a-b)(a+b-1)}{2z} \right)
\end{align}
$$
が示された。$a=1/2,b=0,z=d/2$とおくと
$$
\begin{align}
E[r] = 2\frac{\Gamma(d/2+1/2)}{\Gamma(d/2)} \sim \sqrt{2d}\left(1-\frac{1}{4d} \right)
\end{align}
$$
と計算できる。分散に関しても
$$
\begin{align}
E[r^2] - E[r]^2 &= 2d- \left( 2\frac{\Gamma(d/2+1/2)}{\Gamma(d/2)} \right)^2 \\
&\sim 2d - 2d\left(1-\frac{1}{2d} \right) \\
&=1
\end{align}
$$
と、定数に収束することを示せる。

数値実験

以降はオマケです。
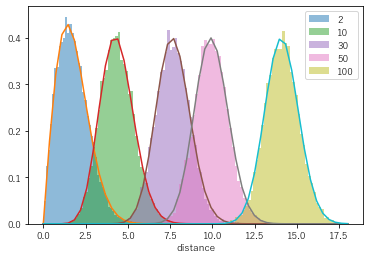
まずは分布形状を確認します。10000件の距離を計算し、理論分布と比較してみます。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats, special

def prob(r,d):
    return 2**(1-d)/special.gamma(d/2) * r**(d-1) * np.exp(-r**2/4)


for dim in [2, 10,30,50, 100]:
    norm = stats.multivariate_normal(cov = np.identity(dim))

    x1 = norm.rvs(10000)
    x2 = norm.rvs(10000)
    r = np.linalg.norm(x1-x2,axis=1)
    plt.hist(r,bins=50,alpha=0.5,density=True,label=dim)
    plt.xlabel("distance")

    x = np.linspace(0,18)
    p = prob(x,dim)
    plt.plot(x,p)
    plt.legend()
plt.show()

計算通りです。
次元が高くなると形状が安定してきて正規分布っぽくなるようです。分散が1に収束することを反映して幅は次元にほぼ依存しないですね。

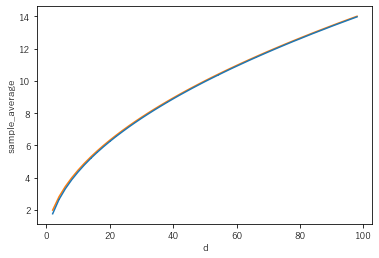
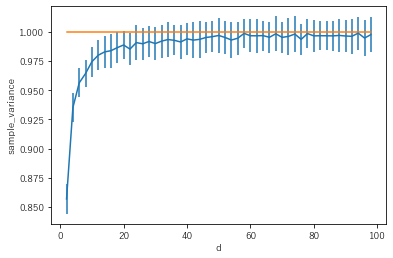
次に平均・分散に関して理論と実験を比較してみます。
10000件の距離から平均分散を計算する過程を100回繰り返し、平均分散のばらつきをエラーバーで書いてみました。(この手の実験の巧い書き方がわかりません...。)
どちらの図も線で描いたものが高次元極限での理論値です。
(ここまで書くのに疲れたので大き目の試行回数で休憩を取りました。)

dims = np.arange(2,100,2)
mean_mean=[]
mean_std =[]
cov_mean =[]
cov_std  =[]
for dim in dims:
    norm = stats.multivariate_normal(cov = np.identity(dim))
    means = []
    covs = []
    for itr in range(100):
        x1 = norm.rvs(10000)
        x2 = norm.rvs(10000)
        r = np.linalg.norm(x1-x2,axis=1)
        means.append( np.mean(r) )
        covs.append( np.cov(r) )

    mean_mean.append( np.mean(means) )
    mean_std.append( np.std(means) )
    cov_mean.append( np.mean(covs) )
    cov_std.append( np.std(covs) )


plt.errorbar(dims,mean_mean,yerr=mean_std)
plt.plot(dims,np.sqrt(2*dims) )
plt.xlabel("d")
plt.ylabel("sample_average")
plt.show()

plt.errorbar(dims,cov_mean,yerr=cov_std)
plt.plot(dims,np.ones_like(dims))
plt.xlabel("d")
plt.ylabel("sample_variance")
plt.show()

平均値に関してはほぼばらつきもなく、低い次元から高次元極限に一致しています。(平均の分散は簡単に計算できて$1/\sqrt{N}=0.01$とかなり小さい)

一方で分散は極限値1の周りで結構ふらついています。分散の分散の理論値は計算していませんが、大き目なんでしょうか。ちょっとした計算でできるはずなので興味があれば教えてください。

まとめ

次元の呪いというその名前も含めてふわっとした事象について、例を絞って客観的かつ厳密なステートメントを挙げてみました。