非情報系大学院生が一から機械学習を勉強してみた #6：学習のテクニック

はじめに

非情報系大学院生が一から機械学習を勉強してみました。勉強したことを記録として残すために記事に書きます。
進め方はやりながら決めますがとりあえずは有名な「ゼロから作るDeep-Learning」をなぞりながら基礎から徐々にステップアップしていこうと思います。環境はGoogle Colabで動かしていきます。第6回はニューラルネットワークの学習を効率よく行う工夫をまとめます。

目次

1. パラメータ更新手法
2. 重みの初期値
3. Batch Normalization
4. 正則化
5. ハイパーパラメータの検証

1 パラメータ更新手法

今回はニューラルネットワークの学習においてキーとなる重要なアイデアについてまとめます。第1章はパラメータ更新の最適化です。これまでパラメータの最適化にはミニバッチデータの勾配を計算しそれが最小となる方向へ進めていく確率的勾配降下法（SGD：stochastic gradient descent）を用いてきました。SGDはシンプルな良い手法ですがより性能の良い手法が存在します。

SGD

以前の記事で紹介したようにSGDは以下のように数式で表現できます。
$$
\boldsymbol{W} \leftarrow \boldsymbol{W} - \eta \frac{\partial L}{\partial \boldsymbol{W}}
$$
ここで更新する重みパラメータを$\boldsymbol{W}$、その損失関数勾配を$\frac{\partial L}{\partial \boldsymbol{W}}$、学習率を$\eta$とします。

SGD

class SGD:
    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key] 

Momentum

Momentumとは「運動量」の意味でSGDに物理的要素を取り入れたものです。数式で以下のように表されます。
$$
\boldsymbol{v} \leftarrow \alpha \boldsymbol{v} - \eta \frac{\partial L}{\partial \boldsymbol{W}} \\
\boldsymbol{W} \leftarrow \boldsymbol{W} + \boldsymbol{v}
$$
$\boldsymbol{v}$は物理で言うところの「速度」に相当し、毎回$\alpha$倍したものを足すことになります。これは一つ前の時間のデータを考慮していると表現できます。つまりイメージ的にはボールが斜面（勾配）に沿って下っている最中は速度分が足され加速、勢い余って斜面（勾配）を上っているときは斜面下向き方向に力を受けるかんじです。これによりパラメータの変化が穏やかになります。
また、上の式を一つにまとめると以下のようになり、SGDに前回の変動分を慣性項として追加したものであるといえます。
$$
\boldsymbol{W} \leftarrow \boldsymbol{W} - \eta \frac{\partial L}{\partial \boldsymbol{W}} + \alpha \boldsymbol{v}
$$

Mememtum

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():                                
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] 
            params[key] += self.v[key]

AdaGrad

パラメータの学習は最適値からほど遠い初めは大きく変化させていき、最適値に近づくと通り過ぎないように小さく変化させていくと良いと考えられます。これを更に発展させ、各パラメータの学習の進み具合に合わせて学習率を適応的に変化させるとよりスムーズに学習が進みそうです。これを実現させたのがAdaGradです。適応的（Adaptive）に勾配（Gradient）を変化させることが名前の由来です。
$$
\boldsymbol{h} \leftarrow \boldsymbol{h} + \frac{\partial L}{\partial \boldsymbol{W}} \odot \frac{\partial L}{\partial \boldsymbol{W}} \\
\boldsymbol{W} \leftarrow \boldsymbol{W} -\eta \frac{1}{\sqrt{\boldsymbol{h}}} \frac{\partial L}{\partial \boldsymbol{W}}
$$
$\odot$は行列の要素積を表します。上の文章と式で述べたようにAdaGradでは勾配の要素積から導出された$\boldsymbol{h}$に依存して更新量を調整することでパラメータの変化量を要素ごとに最適なものに調整できます。

AdaGrad

class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]  #AdaGrad
            # self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]  #RMSProp
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

こちらの実装も前の2つと同様式を素直に実装したものですが、一つ異なるのが最終行で$\boldsymbol{h}$に1e-7が足されてるところです。AdaGradでは式で表されていたように$\sqrt{\boldsymbol{h}}$での除算が含まれているので0割りが発生しないように微小量を加えています。
AdaGradは過去の勾配を全て記録するため学習を進めれば進めるほど過去のデータが増加し更新度合いが低下します。また、学習のはじめに大きな勾配が記録されたときも以降の変化率が極端に小さくなってしまいます。これを防ぐため過去の勾配を徐々に忘れていく手法がRMSPropです。実装例でコメントアウトしてあるように$\boldsymbol{h}$の更新時に忘却係数を追加すれば簡単に書き換えることができます。

Adam

Momemtumの前の時間のデータを用いるアイデアと、AdaGradのパラメータごとの最適更新ステップのアイデアを融合させたものがAdamです。ここではコードだけ載せあまり踏み込まないことにします。

Adam

class Adam:
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)         

        for key in params.keys():
            #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
            #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])

            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

            #unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
            #unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
            #params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)

これまで見てきた4つの方法について探索結果を比較します。関数$y=\frac{1}{20}x^2+y^2$に対して$(x, y)=(-7.0, 2.0)$からスタートさせ最適化を行います。

最適化手法の比較

from collections import OrderedDict

# 関数定義
def f(x, y):
    return x**2 / 20.0 + y**2

# 微分値
def df(x, y):
    return x / 10.0, 2.0*y

# 位置
init_pos = (-7.0, 2.0)   #初期値
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0

# 最適化方法
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)

idx = 1

# 最適化処理
for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]

    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])

        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)

    # 関数輪郭プロット
    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
    X, Y = np.meshgrid(x, y) 
    Z = f(X, Y)

    mask = Z > 7
    Z[mask] = 0

    # 輝点プロット
    plt.subplot(2, 2, idx)
    plt.subplots_adjust(wspace=0.4, hspace=0.7)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")
plt.show()

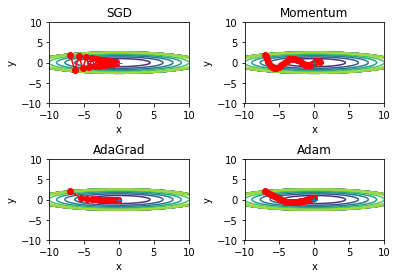図からも分かるようにこの関数は$y=0$付近の多くの地点で平坦となっています。そのためその瞬間瞬間の勾配を考えるSGDでは図のようにジグザグに進んでしまい非効率です。Mementumでは前回の値の影響を加えることでジグザグ度合いが軽減されています。更に学習率の最適調整を行うAdaGradでは更に最適値へ効率的に向かっていることが分かります。これはy軸方向は勾配が大きいためはじめは急速に変化し、その後は更新ステップが小さくなるよう調整されるためだと考えられます。Adamも効率的に進んでいますが、今回はAdaGradの方が効率よく進んでいるようです。どの最適化手法が良いかは問題によって異なり、一概にこれがいいと言うことはできないため注意が必要です。

2 重みの初期値

ニューラルネットワークの学習で初期重みの設定は特に重要です。この設定によって学習がうまくいくかどうかが大きく左右されます。単純に初期値というと全て0にしたくなりますが、（正確には0でなくても均一な値）これはダメなようです。なぜなら初期入力値が同じということは2層目に入力される値もすべて同じになり、そこからは同じ値のパラメータが出力されてしまいます。こうなるとニューロンをいくつも持っている意味がなくなってしまい学習がうまく進みません。そこで重み初期値には不均一なランダム値を設定する必要があります。

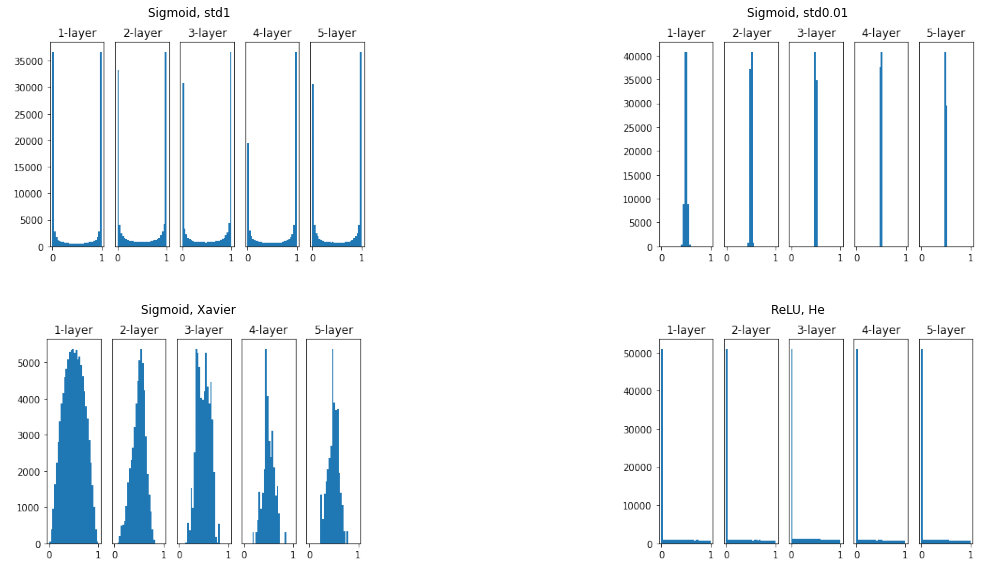以上の図は5層ニューラルネットワークに異なる重みの初期値を与え隠れ層のアクティベーション（活性化関数後の出力）の分布を調べたものです。活性化関数は表記の通り初めの3つがSigmoid、残り1つがReLUを使っています。
ガウス分布に従うランダムノイズを初期値として、その標準偏差を1に設定したものが1つめです。こちらではSigmoid関数の出力が0か1に偏っているため両端に近づくほど微分値が0になる、すなわち勾配がなくなり、学習が進まなくなります。これを「勾配消失問題」と言います。
では逆に標準偏差を0.01と小さくするとどうでしょう？これの結果が2枚目ですが、先程述べたように初期値が均一であると出力が同じになり多数のニューロンがある意味がなくなっていることが確認できました。これはネットワークの表現力の点であまりよくありません。
ではどうすればいいのでしょう？その答えが3、4枚目です。

Xavierの初期値

上のような問題を避けるため、Sigmoid関数を用いるときはXavierの初期値が広く用いられます。これは前層のノード数を$n$としたとき$1/\sqrt{n}$の標準偏差を持つ分布を使うという方法です。このときの結果が3枚目でこれまでより広がりを持った分布になっていることが分かります。

Heの初期値

一方、ReLU関数を用いるときはHeの初期値を用いるとよい結果が得られることが知られています。これは前層のノード数を$n$としたとき$\sqrt{2/n}$の標準偏差を持つ分布を使うという方法です。直観的にはSigmoidが±1の範囲で変化したのに対しReLUでは0~1の範囲になったためより広がりを持たせるために係数を大きくしたと理解できます。その結果が4枚目で層を深くしてもデータの広がりが一定になり、学習が進みやすいと考えられます。

3 Batch Normalization

Batch Normalizationは名前の通り学習を行うミニバッチに対してデータ分布が平均0、分散1の正規分布になるように正規化を施します。すなわちミニバッチ$B= \{x_1, x_2, \cdots , x_m\}$に対して以下の変換処理を行います。
$$
\begin{align}
\mu_B &\leftarrow \frac{1}{m} \sum_{i=1}^m x_i,\\
\sigma_B^2 &\leftarrow \frac{1}{m} \sum_{i=1}^m (x_i - \mu_B)^2,\\
\hat{x}_i &\leftarrow \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \varepsilon}}
\end{align}
$$
ここで$\mu_B, \sigma_B^2$はそれぞれ平均、分散を表し、微小量$\varepsilon$を足すことで0割りを避けています。
Batch Normalizationを加えることにより学習係数を大きくすることができ学習を早く進行させることができる、重み初期値にロバストになる、過学習を抑制するという効果があります。

4 正則化

訓練データのみに適応しすぎてしまい他のデータにはうまく対応できない状態を過学習といいます。これを防ぐ手法を2つ紹介します。

Weight decay

過学習は重みパラメータが大きな値をとることによって生じることが多いとわかっています。そこで重みが大きな値を取らないようペナルティを設けます。ニューラルネットワークの学習は損失関数の値を小さくすることが目標であるため、例えば損失関数に重みの2乗ノルム$\frac{1}{2}\lambda\boldsymbol{W}$を加算します。ここで$\lambda$は正規化の強さを決定するハイパーパラメータ、頭の$\frac{1}{2}$は微分したときに綺麗な形になるための調整係数です。このようにすると損失関数を小さくするためには重みパラメータの値もある程度小さくなくてはいけないという拘束条件が生じ、重みが大きくなりすぎるのを抑制できます。

Dropout

より複雑なモデルに対応したアイデアとしてDropoutがよく用いられます。これは訓練時に隠れ層のニューロンをランダムに選び、そのニューロンをネットワークから削除します。これによって毎回微妙に異なるネットワークで学習を行うことになり、過学習が起こりにくくなります。

5 ハイパーパラメータの検証

学習を行っていくには重みやバイアスなどニューラルネットワークの学習によって自動で決定されていくパラメータの他に各層のニューロン数やバッチサイズ、学習率などあらかじめ人間が決定しておく必要があるパラメータが存在します。これらをハイパーパラメータといいます。これらを決めるにはまず検証データを用意しなくてはなりません。検証データはニューラルネットワークの訓練データ、テストデータとは別のデータを用意します。理由は別に訓練データを用意したのと同様、検証データのみに過学習してその他のモデルに適応できなくなってしまう事態を防ぐためです。
ハイパーパラメータの最適化には理論的にこうすればよいという手法がないようです。一般には"適当"に繰り返しやってみて良い値を絞り込んでいくしかないようです。以下のような流れで進めていきます。

ステップ0

1. ハイパーパラメータの探索範囲を設定する。10の階乗スケールでざっくりとでよい。
2. 設定された範囲内からランダムにサンプリングする。
3. ステップ2でサンプリングされたハイパーパラメータの値を使用して学習を行い、検証データで認識精度を評価する（ただし繰り返し行い時間がかかってしまうためエポック数は小さめで良い）。
4. ステップ2、3をある程度（100回など）繰り返し、それらの認識精度の結果からハイパーパラメータの範囲を狭める。

以上のステップハイパーパラメータの範囲を絞り込んでいき、ある程度絞り込めた段階でその範囲からハイパーパラメータの値を一つ選び出します。

参考文献

ゼロから作るDeep-Learning
ゼロから作るDeep-Learning GitHub
深層学習 (機械学習プロフェッショナルシリーズ)