非情報系大学院生が一から機械学習を勉強してみた #4：最急降下法

#はじめに
非情報系大学院生が一から機械学習を勉強してみました。勉強したことを記録として残すために記事に書きます。
進め方はやりながら決めますがとりあえずは有名な「ゼロから作るDeep-Learning」をなぞりながら基礎から徐々にステップアップしていこうと思います。環境はGoogle Colabで動かしていきます。第4回はニューラルネットワークによる学習の準備として最急降下法を整理します。

#目次

1. 数値微分
2. 偏微分
3. 勾配
4. 最急降下法

#1. 数値微分
ご存知の通り微分は以下のように表せます。
$$
\frac{df(x)}{dx}=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}\tag{1}
$$
$h$を極限まで小さくすればよいので以下のような数値計算による実装が考えられます。

悪い実装例

def numerical_diff(f, x):
    h = 10e-50
    return (f(x+h) - f(x)) / h

この実装は良くありません。理由は2つあります。

• 計算機内部の丸め誤差を無視している
• 差分誤差を無視している

計算機内部の丸め誤差を無視している

計算機内部ではビット演算で動いているので有効桁数が無限にある訳ではありません。したがって$10^{-50}$に設定しても計算機では$0$に丸められてしまい、微分できません。一般に$h$は$10^{-4}$程度にするのが良いと知られているそうなのでその値を使います。

差分誤差を無視している

微分は接点$x$における接線を意味しますが、数値計算の式で計算できるのはあくまで$x$と$(x+h)$の間の傾きを表現しているものにすぎません。1点目の理由から$h$を極限まで（理論的には無限小まで）小さくすることができないため真の微分値と傾きの値にどうしても誤差が生じてしまいます。

これらの解決法として誤差を小さくするために以下の式を考えます。
$$
\frac{df(x)}{dx}=\lim_{h\rightarrow 0}\frac{f(x)-f(x-h)}{h}\tag{2}
$$
式(1)を前方差分、式(2)を後方差分と呼びます。式(1)と式(2)を足します。
$$
\begin{align}
2\frac{df(x)}{dx} &= \frac{f(x+h)-f(x)}{h} + \frac{f(x)-f(x-h)}{h} \
2\frac{df(x)}{dx} &= \frac{f(x+h)-f(x-h)}{h} \
\frac{df(x)}{dx} &= \frac{f(x+h)-f(x-h)}{2h}\tag{3}
\end{align}
$$
式(3)を中心差分といいます。この式が最も誤差が小さくなり、数値微分の計算に使われます。
今回は中央差分式の導出のみ行いましたが、最も誤差が小さくなることをTeylor展開を使ってしっかり証明した記事がありました。
数値微分における3つの差分とその誤差について

よって、数値微分は以下のように実装できます。

数値微分

def numerical_diff(f, x):
    h = 1e-4
    return (f(x+h) - f(x-h)) / (2*h)

#2. 偏微分
微分の計算を変数ごとに行えば偏微分になります。すなわち
$$
\frac{\partial f(x_0)}{\partial x_0} = \frac{f(x_0+h)-f(x_0-h)}{2h}
$$
となります。詳しくは勾配で。

#3. 勾配
変数ごとの偏微分をまとめて計算すると勾配になります。すなわち
$$
\nabla f =
\begin{bmatrix}
\frac{\partial f(x_0)}{\partial x_0} \
\frac{\partial f(x_1)}{\partial x_1}
\end{bmatrix}

\begin{bmatrix}
\frac{f(x_0+h)-f(x_0-h)}{2h} \
\frac{f(x_1+h)-f(x_1-h)}{2h}
\end{bmatrix}
$$
となります。以下のように実装できます。

勾配

# 関数定義
def f(x):
    return x[0]**2 + x[1]**2

# 勾配
def numerical_gradient(f, x):
    h = 1e-4
    grad = np.zeros_like(x)

    for idx in range(x.size):
        tmp_val = x[idx]
        # f(x+h)
        x[idx] = tmp_val + h
        fxh1 = f(x)
        # f(x-h)
        x[idx] = tmp_val - h
        fxh2 = f(x)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val
    
    return grad

# 勾配計算
numerical_gradient(f, np.array([3.0, 4.0]))     #array([6., 8.])

上の実装例ではx.size回ループを回して変数ごとの偏微分を行っていることになります。勾配は現在地点から最小値への向きを含めた傾きと言えます。

#4. 最急降下法
勾配は現在地点から最小値への向きを含めた傾きなので、勾配の向きへの移動を繰り返せば最小値にたどり着けそうです（現実は局所解や傾きが0になる鞍点であることもあります）。大まかにはこの発想で最小値を探そうというのが再急降下法です。再急降下法では勾配の向きに一定距離だけ移動し、移動した新しい点で再び勾配を計算します。その新たな勾配に基づいてまた一定距離移動し移動先でまた勾配を更新し……を収束するまで繰り返します。私たちが良く知らないところに行くときちょっと歩いたら地図を見て合っているか確認し（必要なら修正し）また目的地に向かうのによく似ています。

式で表現すると以下のように書けます。
$$
x_n(k+1) = x_n(k) - \eta \frac{\partial f\left(\boldsymbol{x}(k)\right)}{\partial x_n}, ~~~n=1, ..., N\tag{4}
$$
$n$は変数数（勾配の例のように$x_0, x_1$ 2変数を用いる場合$N=2$）、$k$はイタレーション数、$\eta$は学習率です。現在の位置$x_n(k)$に対して勾配に学習率をかけて変化率を調整したものを引くことで次の位置$x_n(k+1)$を決定します。このイタレーション処理を
$$
k = k_{max}
$$
すなわちイタレーション回数が規定回数終了するか、
$$
|x_n(k+1) - x_n(k)| < \varepsilon
$$
すなわち更新量が規定量より小さくなり収束するまで繰り返します。
実装は以下のようにできます。

再急降下法

matplotlib.rcParams["mathtext.fontset"] = "cm"
matplotlib.rcParams['contour.negative_linestyle'] = 'solid'

# 再急降下法
def gradient_descent(f, init_x, lr, k_max):
    x = init_x
    x_history = [] 

    for i in range(k_max):
        x -= lr * numerical_gradient(f, x)      #再急降下法計算
        x_history.append( x.copy() )            #データ保存
    return x, np.array(x_history)

# 関数定義
def f(x):
    return 3*x[0]**2 + x[1]**2

# 再急降下法計算
lr = 0.01                           #learning rate
k_max = 400                         #イタレーション数
init_x = np.array([-3.0, 3.0])      #初期位置
x, x_history = gradient_descent(f, init_x, lr, k_max)
# 収束確認
plt.plot(x_history[:,0], label="$x_0$")
plt.plot(x_history[:,1], label="$x_1$")
plt.xlabel("$k$", fontsize = 18);
plt.ylabel("value", fontsize = 18);
plt.legend(fontsize = 18)
plt.show()

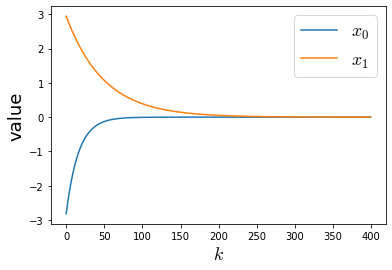
gradient_descent関数で式(4)に従って再急降下法を実装しています。x_historyで$k$回目の値を記録しています。これは後で使います。
後半で実際にパラメータを設定し再急降下法の計算を実行しています。表示させている図は各イタレーションでの$x_0, x_1$の値です。今回の関数は$(x_0, x_1) = (0,0)$で最小値をとるので共に0になれば収束したことを意味します。よって400回のイタレーションが終了するまでには$x_0, x_1$ともに収束していることが確認できました。

次は計算した結果を等高線上にプロットしてみます。

再急降下法結果の確認

# 輪郭（等高線）プロット関数
def plotContour(plt):
    # meshgrid設定
    N =100
    x0 = np.linspace(-4, 4, N)
    x1 = np.linspace(-4, 4, N)
    X0, X1 = np.meshgrid(x0, x1)
 
    # 目的関数値
    Y = f([X0, X1])
 
    # 等高線をプロット
    M = 30
    levels = np.linspace(np.min(Y), np.max(Y), M) 
    plt.contour(X0, X1, Y, colors="k", levels = levels);

# 等高線をプロット
fig = plt.figure()
ax = fig.add_subplot(111)
plotContour(ax)
plt.xlabel("$x_0$", fontsize = 18);
plt.ylabel("$x_1$", fontsize = 18);

# 再急降下法で記録された点をプロット
for i in range(k_max):
    ax.plot(x_history[i, 0], x_history[i, 1], "-o", color = "red", markeredgecolor = "black", markersize = 5, markeredgewidth = 0.5);

plt.show()

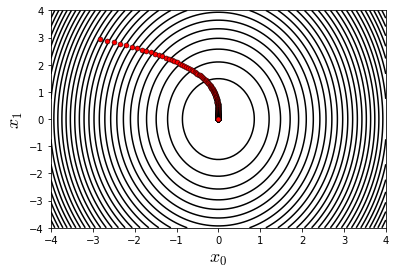
plotContour関数で今回設定した関数$f(\boldsymbol{x}) = 3x_0^2+x_1^2$を2次元プロットします。その図上に先ほど記録したx_historyをプロットすることで再急降下法によって始点からどのように収束点まで向かっているか観測できます。図より確かにその時々の点で最も値が小さくなる方向に向かって進んでいることが確認できました。

さて、なぜ機械学習で再急降下法が用いられるのでしょうか？
機械学習では教師データに沿うよう最適なパラメータ（重みとバイアス）を学習していきますが、何をもって最適とするかの評価手法が必要です。この評価手法として評価関数というものを用いて、その値が最小になることを目指します。この最小を探すという操作に再急降下法が必要になります。

#参考文献
ゼロから作るDeep-Learning
ゼロから作るDeep-Learning GitHub
深層学習 (機械学習プロフェッショナルシリーズ)