このポストは Inside of Deep Learning あるいは深層学習は何を変えるのか から分割したものです。全体があまりに長くなってしまったので別のページにしました。
できるだけ短い時間で初心者にも分かるように、数学的な内容を直感的な説明に置き換えて分かりやすく説明しようと試みています。ただしそのために大分抽象的に言い切ってしまっているところがあります。
もっといろいろなケースが存在する場合や、数学的に見ると厳密には正しくない場合もあります。ご容赦下さい。
基本要素
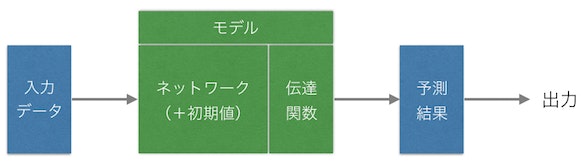
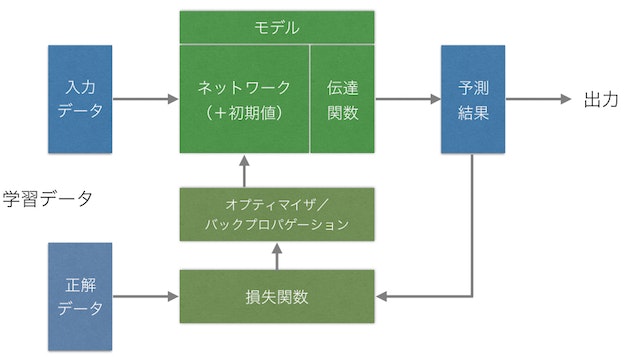
DLのシステムを構成する要素として、初期値、モデル、損失関数、オプティマイザ、バックプロパゲーションに分けて説明します。
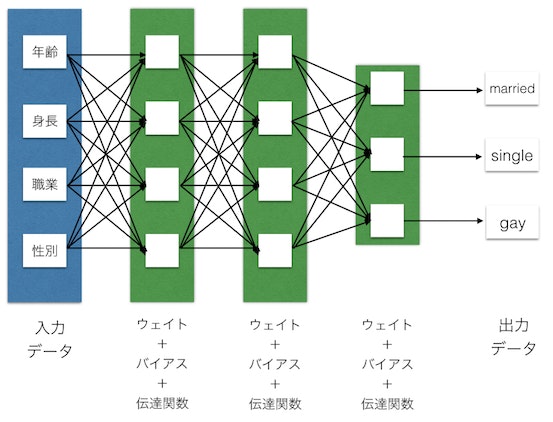
上記はDLに限らず基本的なシステムに言える事ですが、入力用のデータをモデルに入れて予測結果を導き出します。基本的には入力と出力はベクトルあるいはマトリックスになり、この流れがフォワードプロパゲーションです。
伝達関数は常に最後にあるものではなくモデルの中で各レイヤとセットで何度も出てくるものですが、イメージ図としての便宜上で簡略して最後に置いておきます。
通常は出力値を予測するだけですが、トレーニング中はこの予測結果をフィードバックします。入力データに対しての正解データ(教師データ)を用意してやり、損失関数という式を使って予測値が正解ととれだけ離れているかを計算します。
これを元に、現在のモデルをどのように修正すれば正解に近づく可能性が高いを計算します。これがオプティマイザです。損失値の勾配とオプティマイザによってネットワークがより強化され、この一連の流れがバックプロパゲーションです。
ネットワークはもともとはランダムの初期値を持っています。これが一度のバックプロパゲーションにより強化され、少しづつフォワードプロパゲーション、バックプロパゲーションを繰り返していく事でシステム内の初期値(パラメータ)が学習していきます。
モデル、伝達関数
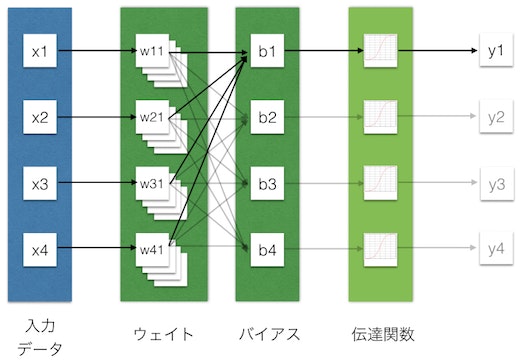
モデル内の実際の計算を見てみましょう。簡便のため一つのレイヤーの局所的な計算を図解します。
x1からx4の入力データ(ベクトル)があったとします。これからこのレイヤーの出力ベクトルy1からy4を計算します。この場合ウェイトは4x4の行列、バイアスは4x1のベクトルです。
y1の計算値は、x1w11 + x2w21 + x3w31 + x4w41 + b1 の値に伝達関数を通したものになります。
大きくはしょって言えば、wの掛け算は各入力に対してどの信号を増幅させるかを決める値です。bの足し算はどのレベルを超えたら反応するように決める閾値で、その後に伝達関数によってある閾値を超えた部分のみ次へ伝えます。
y1からy4までまとめて計算しようとするとこれはxベクトルにw行列をかけてbベクトルを足すことになり、すなわちただの行列演算となります。これがビデオカード(GPU)がDLを圧倒的に高速化できる理由です。
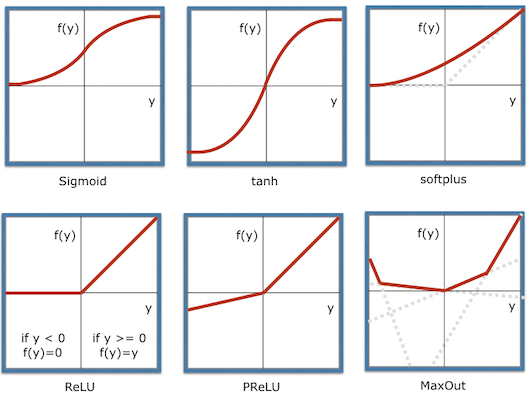
伝達関数はいろいろなものがありますが、ここがシステムを非線形にして表現力を大きく上げる重要な特徴だと思います。
現在ではReluと呼ばれる下記のような関数が一般的です。これはyが負の場合は0、それ以上の場合はyと同じ値を返す関数です。ゼロ以下になった信号をカットして全て0にする単純なものですが、これにより得られた結果の中から注目する値の部分だけを選択的に後ろに伝えることができるようになります。
伝達関数(Transfer Function)あるいは活性化関数(Activation Function)は後に説明するバックプロパゲーションを行うために__道関数が求められるものを利用します__。昔はsigmoidや tanhを使っていましたがこれらではyが大きくなると勾配が0に非常に近くなり、層を重ねてディープにすると勾配計算時に入力に近い層へ逆伝播する量が消えていく問題がありました。そのためsoftplusやReLUが考案され、yが1より大きくなる場合でも勾配を保持するよう改良されました。特にReluは計算が早いため非常に有効で沢山のディープなネットワークで利用されました。
さらにPReluや複数の線形関数からの最大値を利用するMaxOutなどが考案されており、データやモデルの構造に合わせて適切なものを選ぶことが大事です。また伝達関数やモデルに合わせてウェイトの初期化の仕方も変わるのでここも注意が必要です。
上記でみたウェイト+バイアス+伝達関数の組みを一つのレイヤーとして複数のレイヤーを接続し順に計算結果を伝えていき最終的な出力を計算します。
初期値
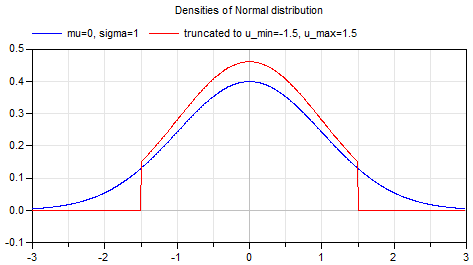
一番最初のウェイト、バイアスの値が初期値となります。モデルが非常に複雑な場合はプレ学習をさせた値を使うこともありますが、通常は正規分布などに乗ったランダムの値(上図 青)や上下で標準偏差の2倍の値でカットしたもの(上図 赤)等を用います。
ランダムな値とは言えモデルが複雑になってくるとこの初期値が重要になるケースも多くなります。
CNN
CNN(Convolutional Neural Network)は厳密にいうと基本要素ではないのですが、画像などではあまりに多く使いますしDLによる既存技術の性能向上に強く寄与していて非常に多く使われているので基本要素として説明します。
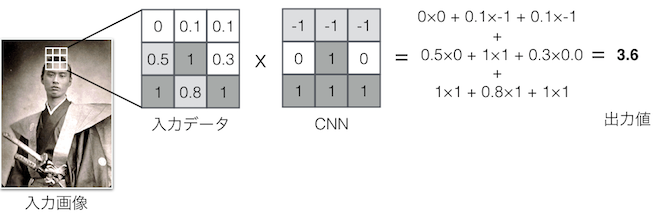
例えば3x3の大きさで説明すると、入力となるデータのそれぞれのマス目に対してそれぞれの係数を掛け算して得られた値を合計したものが出力値となるユニットです。これは縦及び横の両方向に対して意味があるデータについて、そのパターンに合致するものを出力するフィルタと言って良いと思います。
入力画像のある点について、その周囲の点も含め3x3の大きさで切り出します。入力の値はその点の明るさです。CNNの各ウェイトを各入力値に掛け算してその合計値を出力します。
ここまでがフォワードプロパゲーションです。
損失関数、教示データ
ここから先がバックプロパゲーション、すわなち学習ステップです。
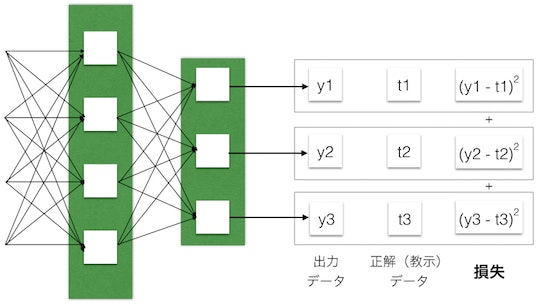
与えた入力データに対しての正解データを用意します。システムの答えがどれだけ正解データからはずれていたかを損失(ロス)として定義します。この値が小さければ小さいほど望ましい状態とします。正解データと入力データとの誤差の2乗和を使うことが多いです。
何故2乗和を使うかというと、正解データと出力データの差が正規分布になっている場合に計算モデルがフィットするからということと、正規分布に乗ってない場合であってもプラス側の誤差でもマイナス側の誤差でも同じ損失にできるということからだと思います。
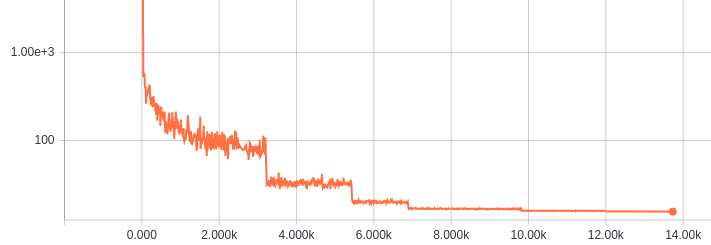
下図は学習が進んだ時のテストセットに対しての損失の変化を対数グラフにしたものです。(ミニバッチを使っているため線がギザギザしているのが特徴です。途中でストンと落ちているところは学習係数を調節しているポイント。)
オプティマイザ
損失を定義したことにより、この損失を効率的に最小にするための数学的問題とすることができます。一般的な機械学習は大体このような問題として捉えられます。
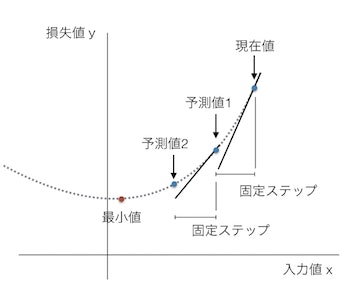
例えば損失の値が下の図の点線のように分布していたとします。現在の値(x)に対しての損失(y)の値が取得できたとします。赤色の最小値が得られるwを見つけることがゴールですが、点線の分布は見えない状態です。
一般的なオプティマイザではまず現在の重み値wでの損失yの傾きあるいは接線を求めます。その後接線をw方向にある固定幅だけ伸ばして次の値となる予測値1を求めます。今度はw=予測値1でのy値と接線を求め予測値2を求めます。これを繰り返して少ない試行回数でyが最小なwを求めることができます。これは勾配法と呼ばれています。DLでは勾配を求められることが重要で、伝達関数を含めモデル内の要素は微分可能なものだけで構成されています。
この場合の固定ステップの大きさが学習係数(Learning rate)あるいは学習率と呼ばれるもので、大きければそれだけ早く最小値を求めることができますが逆に最小値を飛び越して発散してしまいます。そのため一般的には学習が進むにつれて学習係数を小さくしていくわけです。近年ではいろいろなオプティマイザやバッチ手法が考案されより複雑なモデルでも短い時間で最適化できるようになってきています。
バックプロパゲーション
さて、上記は損失yに対しての重みwが一つだった場合での例です。実際は大量のウェイト、バイアスが多層に渡って存在します。この場合を簡単に見ておきましょう。あともう少し!
現在だとバックプロパゲーションというとシステムの予測結果と正解データとの差からウェイトを更新し学習させること全般を指すことが多いですが、本来は多層レイヤでの各ウェイト、バイアス値に対する損失の傾きを順次求める計算部分のみを指すようです。
ウェイトやバイアスの更新原理を式で説明すると非常に難解になってしまうため、ここでは式は省略して全体の流れだけを説明します。順番的にはフォワードプロパゲーションとは逆で、出力層に近いレイヤーから順に重みを更新していきます。
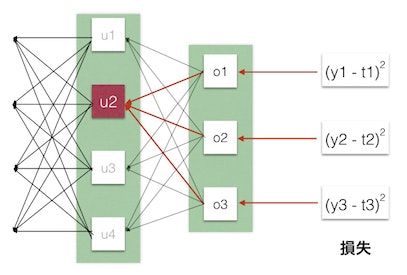
例えば図のu2ユニットの場合、o1-o3の誤差と勾配からu2のウェイトをどれだけ変えれば損失がどれだけ変わるかを予測し、勾配法を用いて局所的な損失が小さくなるように更新します。さらにこの時のu2の予測値(勾配)を用いてu2より一つ前のレイヤーのウェイトについても、これを変えれば損失がどれだけ変わるかを計算して順次更新していきます。
__この方法は非常に高速です。__例えば各ウェイトごとに僅かな値だけ変更してみて各ウェイトに対する損失の勾配を求めるとします。そうすると数百万というウェイトの数だけ損失を再計算する必要がでてしまうのです。バックプロパゲーションでは各段の出力値を保存しておけば一度の損失計算と同程度の計算量で更新をすることができるのが特徴なのです。
ちなみに、各ウェイトでの損失の傾きを求めるために 自動微分 を使います。多層パーセプトロンにおける自動微分とバックプロパゲーションが自分でディープラーニングの学習ソフトを作る場合に一番難しい部分になると思います。
基本要素まとめ
上記で見てきた通り、初期値、モデル、損失関数、オプティマイザが基本要素となってDL(ニューラルネット)の学習を構成しています。オプティマイザやバックプロパゲーションの仕組みなどを理解していなくてもモデルを書くことはできるのですが、難しいモデルを精度良く改良していくためにはこれらの基本要素への十分な理解が必要になります。
ともあれ最後に一つ基本事項として伝えたいものがあるとすれば、それは__DLモデルの持つその表現力です。__ニューラルネットはどんなに複雑な関数でもそれを近似できる可能性があり、そこにRNNやLSTMなどの構造的な改良が加えられて大きな発展を遂げています。