Houdiniでアルゴリズミック・デザイン～Isosurface編
この記事はHoudiniアドベントカレンダー2017 10日目の記事です。
本文最下部に記事で使っているHoudiniファイルのダウンロード先のリンクがあります
Isosurfaceとは
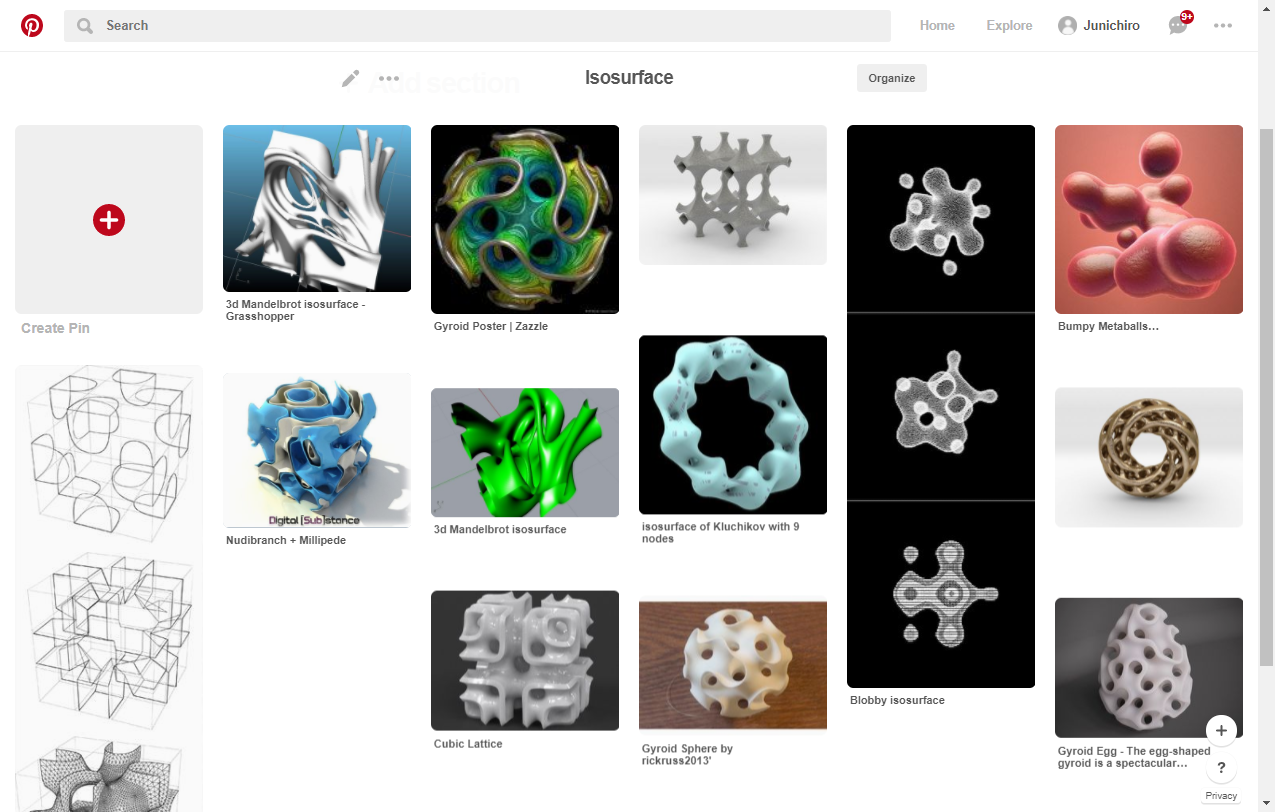
Isosurface は建築界隈ではおなじみのワードで、空間上に数値が与えられた点群があると考えた時（ボクセル空間）、その点群上の近い数値同士を結んだ時にできる面のことです。
- Pinterest上のisosurfaceで検索すると出て来る画像
このボクセル空間から面をを作るためのアルゴリズムとして**Marching Cube** というものがありますが、ありがたいことに Houdini を使うことで簡単にこのボクセル空間が作れ、またそのボクセル空間からMarching Cubeと思われるアルゴリズムを使ったノードでメッシュを作成することが可能です。
この記事ではその方法を説明したいと思います。
数理的にボクセル空間をコントロールするための関数を集める
なにはともあれボクセル空間上の点に数値を与えていくことが必要になりますが、今回はお題として アルゴリズミック・デザイン とよんでいることもあり、ボクセル空間上の点の位置情報（XYZ座標）を利用してsineやcosineといった関数を使って数理的に数値を決定してみたいと思います。
ただ闇雲に関数を作ってもきれいな面ができるとは限らないので、とりあえず先例はないかなと探します。ざっと検索した結果、すぐにでも使えそうな関数が載っているページが２つ見つかったので、今回はそちらに載っている関数を拝借して、一部 パラメトリック にすることを前提に利用してみたいと思います。
- Metamagic "3D Printing with Isosurfaces"
- stackoverflow "How do I reproduce this heart-shaped mesh in MATLAB?"
Houdiniのノードのセットアップ
ボクセル空間をコントロールするための関数が集まったところで、次にHoudiniのノードのセットアップです。今回は関数を入力することがメインなので、ノードのネットワーク自体は簡素なものにしたいと思います。
Step 1: Boxを作成
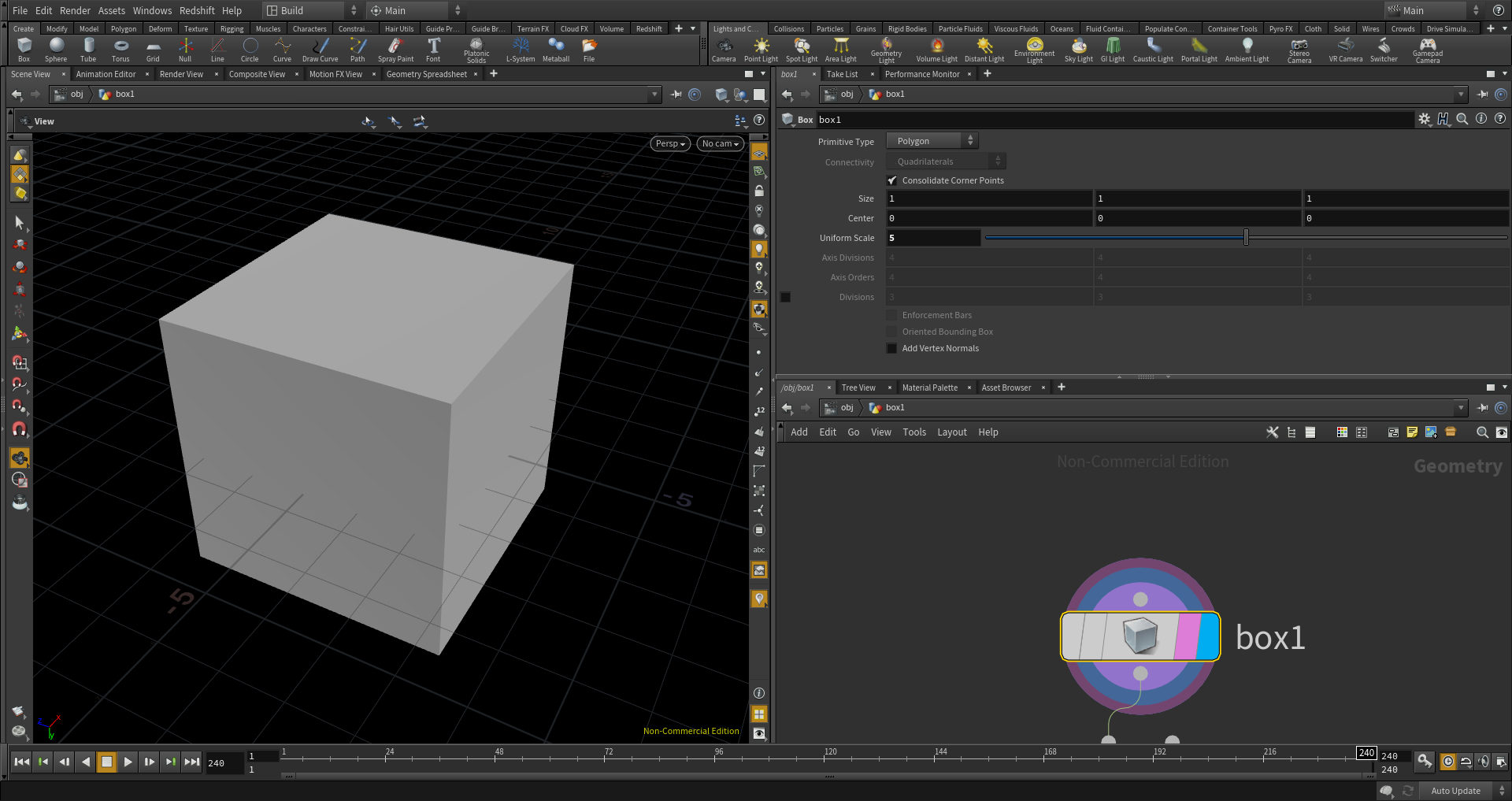
ボクセル空間の領域となるBoxを作成します。
（Boxノード：Uniform Scale=5)
Step 2: BoxからFog Volumeを作成
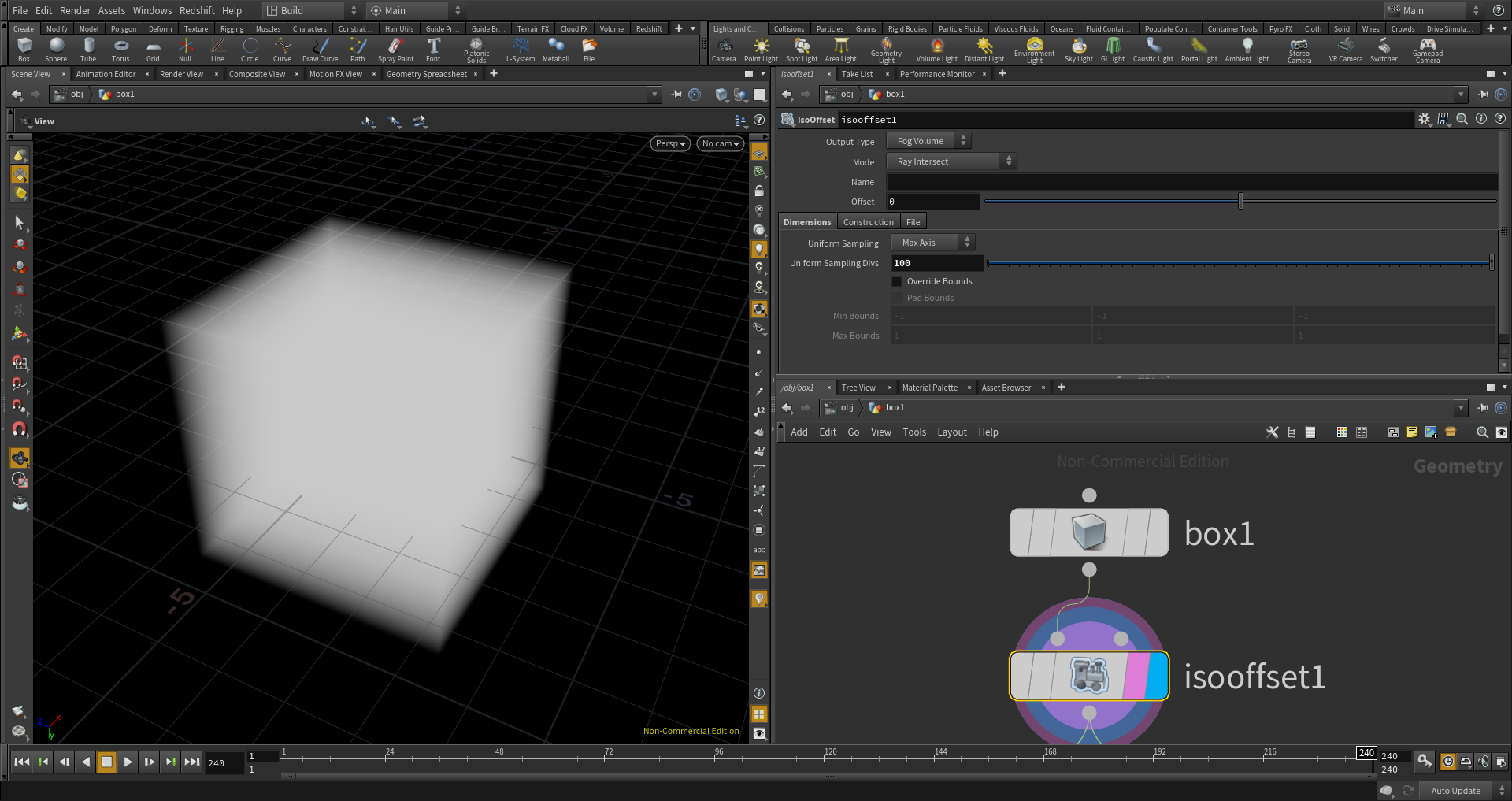
Houdini上のボクセル形式の一つであるFog Volumeをボックスから作成します。
(Isooffsetノード：Uniform Sampling Divs=100)
Step 3: 空のVolume Wrangleを６個つなげる
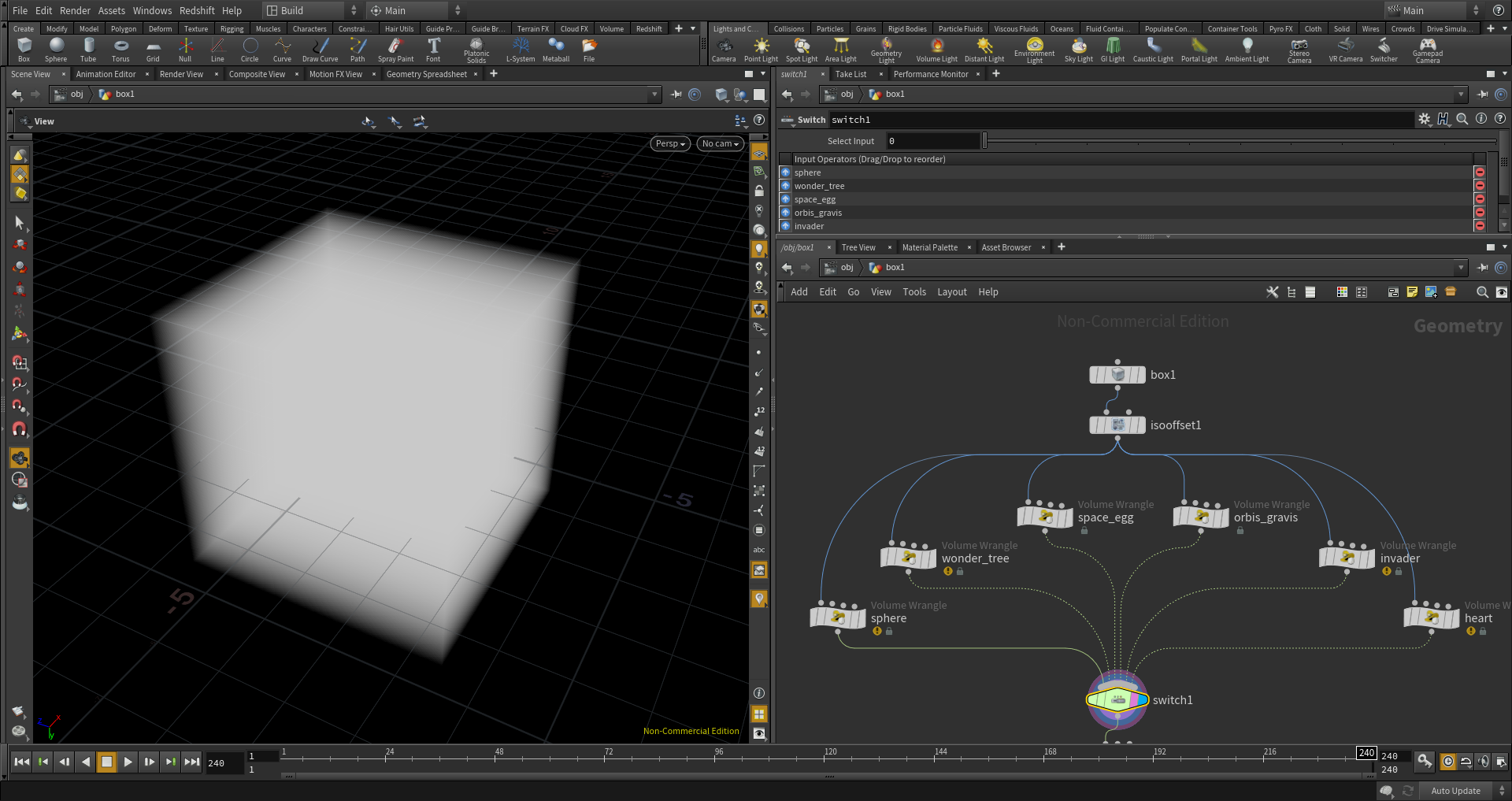
関数の参照先の名称にのっとり、Volume Wrangleノードの名前をそれぞれ"sphere", "wonder_tree", "space_egg", "orbis_gravis", "invader", "heart"にします。最後にその６つのVolume WrangleをSwitchノードで切り替えられるようにします。
Step 4: FogをSDFに変換する
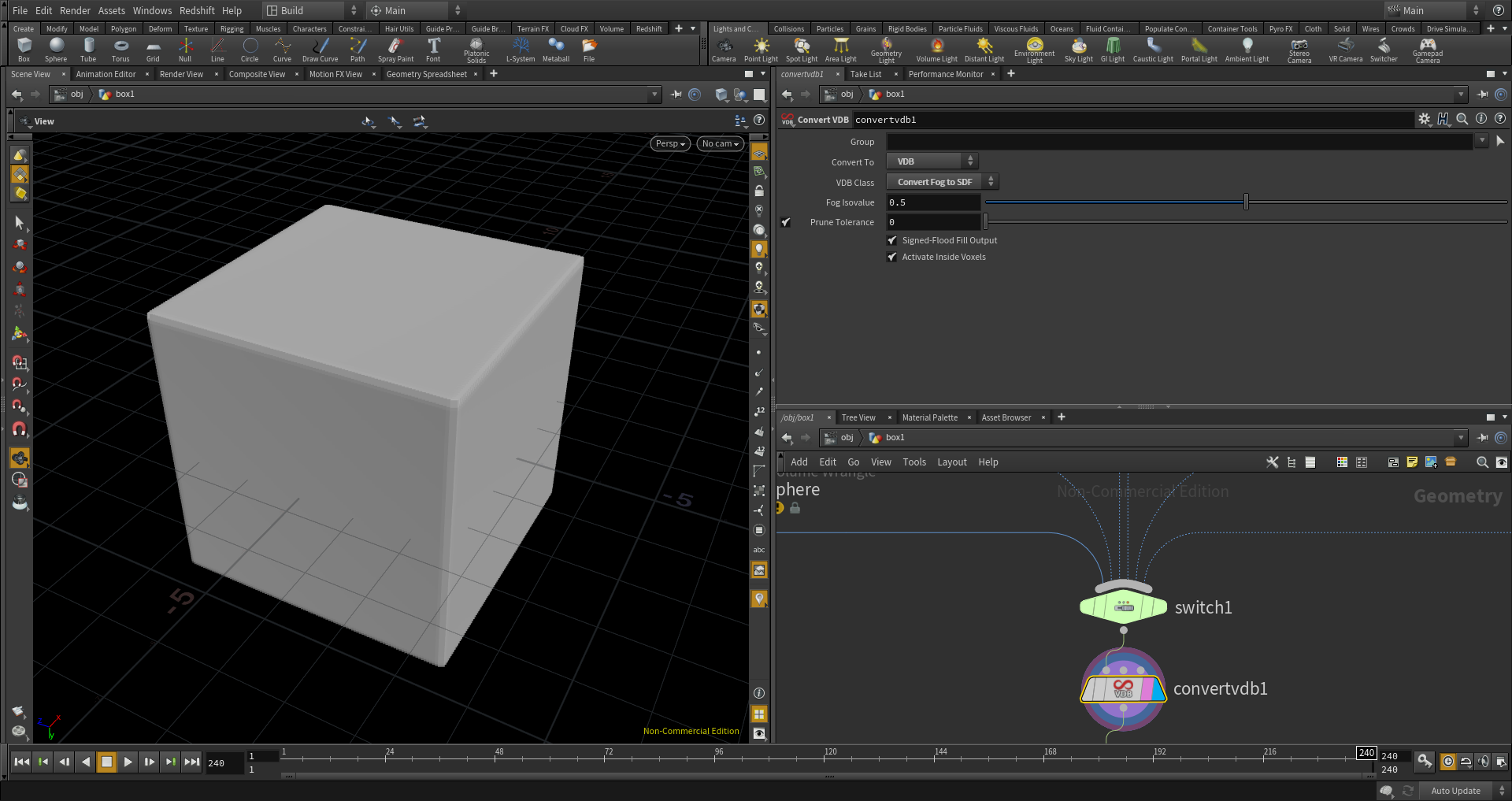
メッシュに変換するために、Fogを一度Houdini上のもう一つのボクセル形式であるSDFに変換します。
(Convert VDBノード：Convert to=VDB, VDB Class=Convert Fog to SDF)
Step 5: SDFをPolygonに変換する
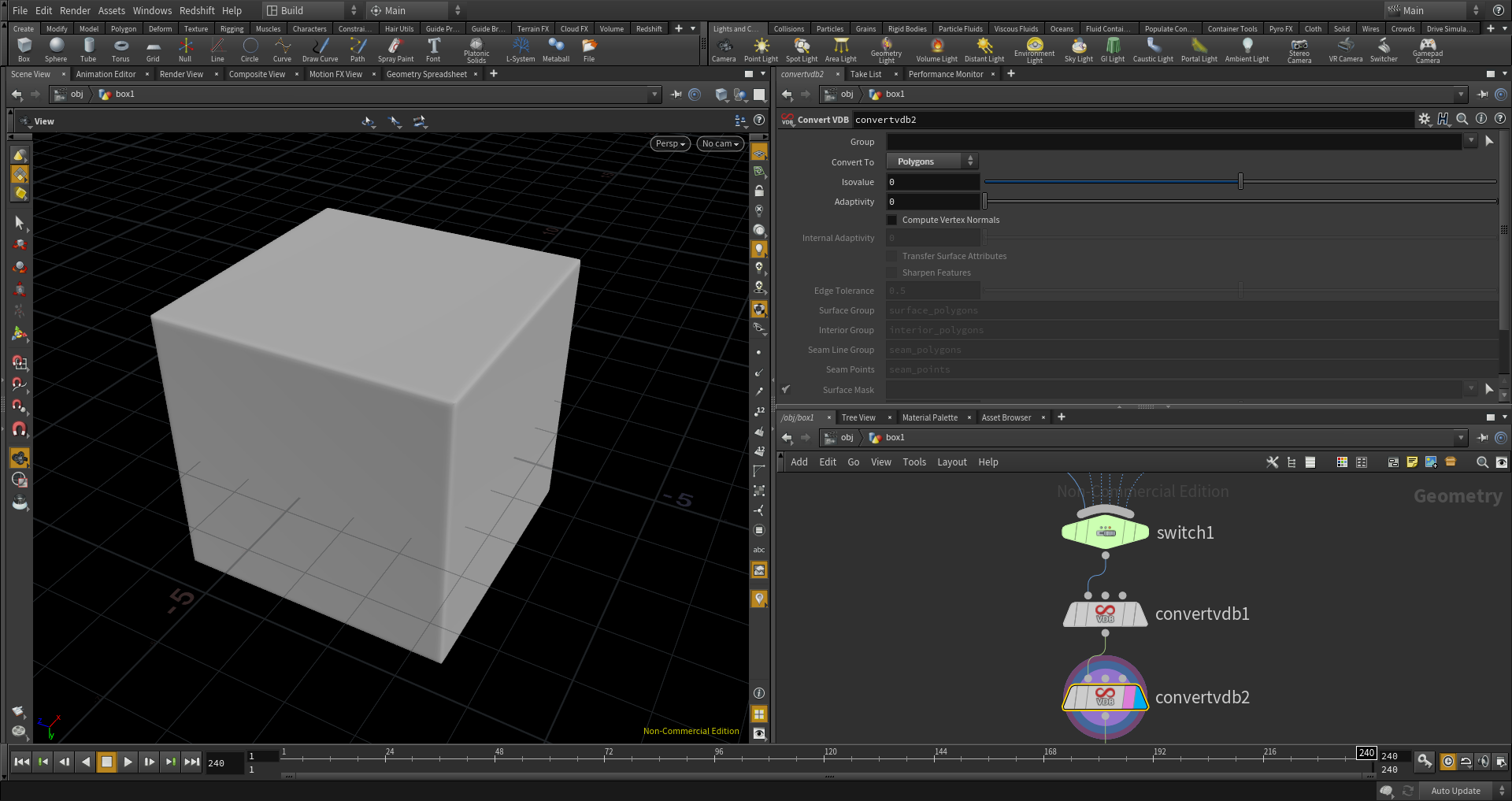
これでボクセル空間がメッシュに変換されました。
(Convert VDBノード：Convert to: Polygons)
Step 6: 色を付ける
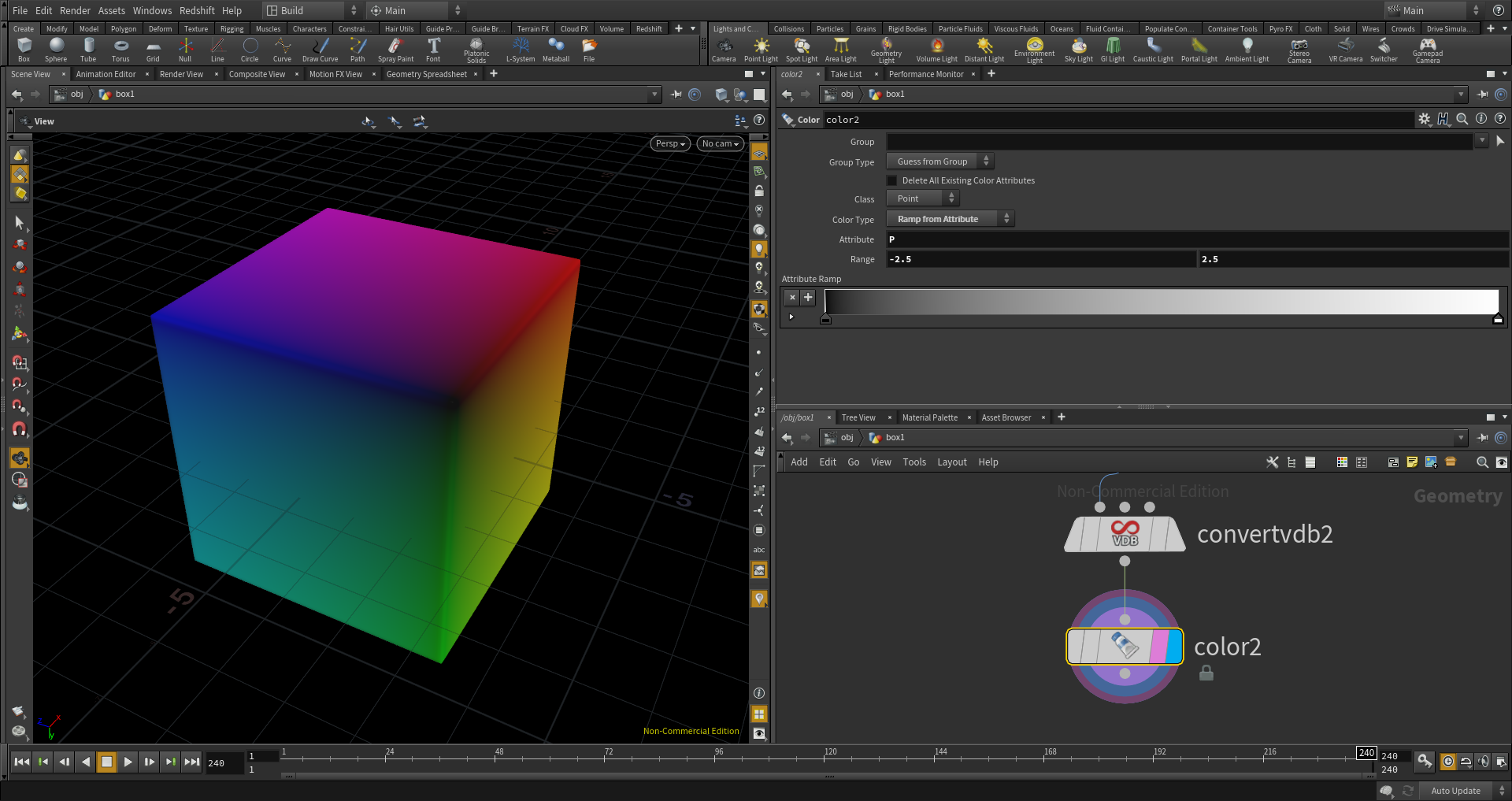
ポイントの位置情報を利用して色をつけます。
(Colorノード：Color Type=Ramp from Attribute, Range= -2.5, 2.5)
関数をVolume Wrangleに入力
これで準備はできたので、早速６つあるそれぞれのVolume Wrangleに参照先URLから拝借してきた関数を入力してみようと思います。
Sphere
まずはMetamagicで一個目で説明しているシンプルな球体から。サイトでは下記のような関数で、半径４の球が表現できるとしています。
The application lets you visualize an implicit, 3D surface, i.e., the solution to an equation in three variables. A sphere centered on origin with a radius of four, for example, would be the solution to the equation
x^2+y^2+z^2-4^2
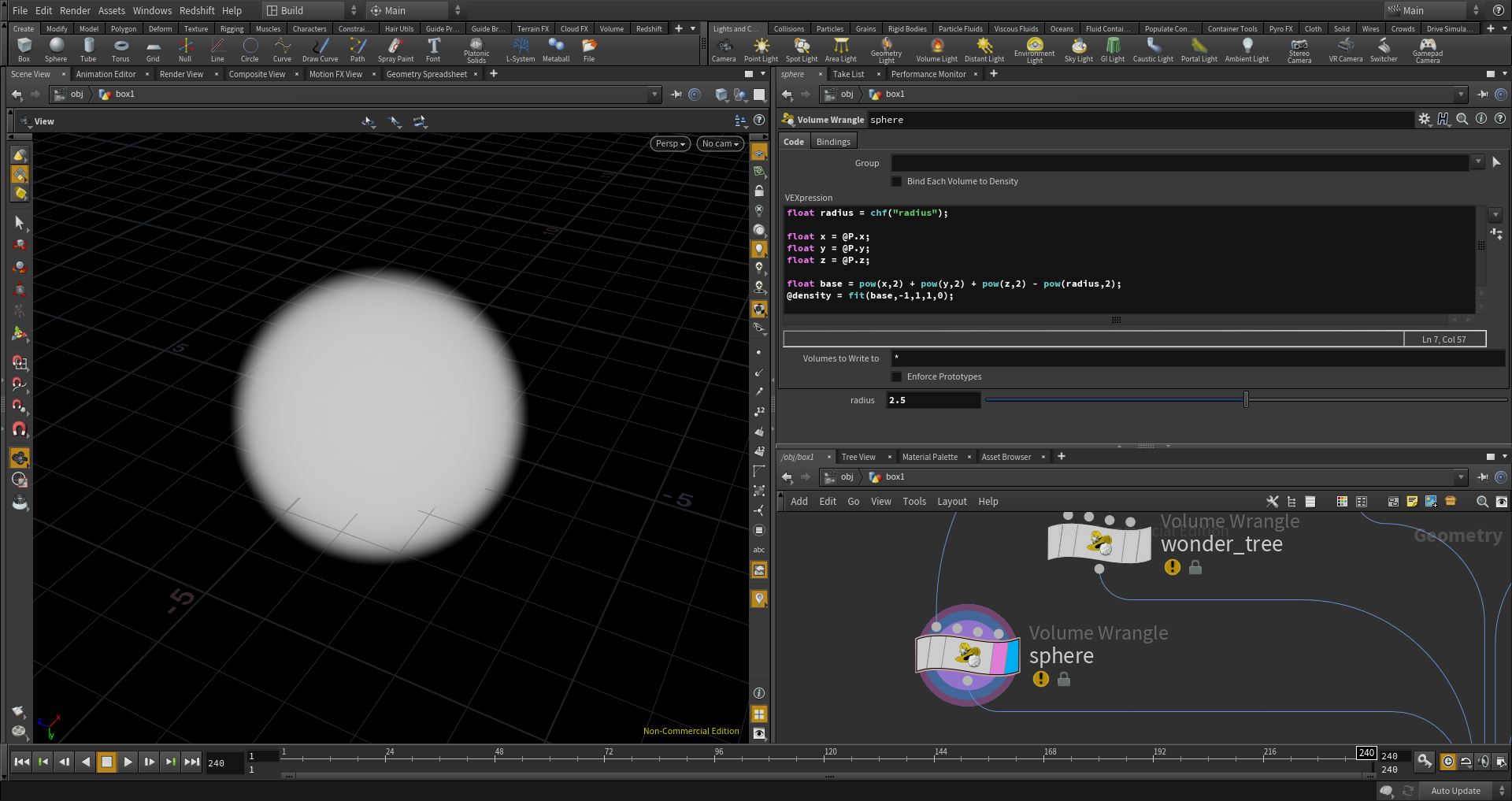
ではこれをVolume Wrangleをつかって、この関数を導入してみたいと思います。
float radius = chf("radius");
float x = @P.x;
float y = @P.y;
float z = @P.z;
float base = pow(x,2) + pow(y,2) + pow(z,2) - pow(radius,2);
@density = fit(base,-1,1,1,0);
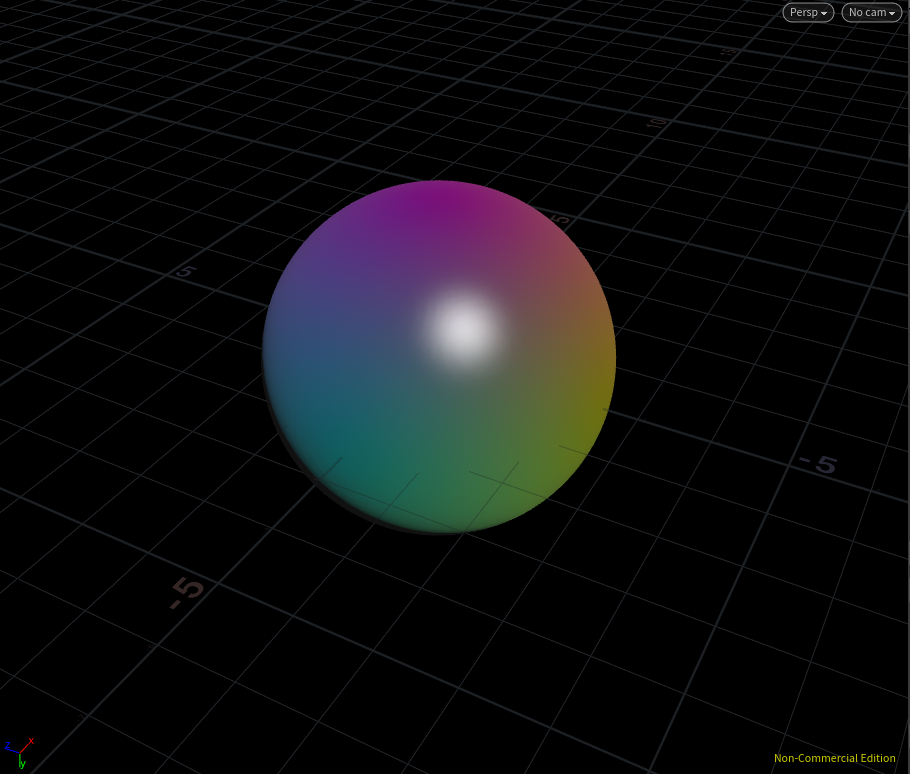
ここでは、radiusというfloatのパラメータを作成して、半径を決定していると考えられる4.0の部分をradiusで置き換えています。結果としてパラメトリックに半径を変えられる球体のフォグができました。
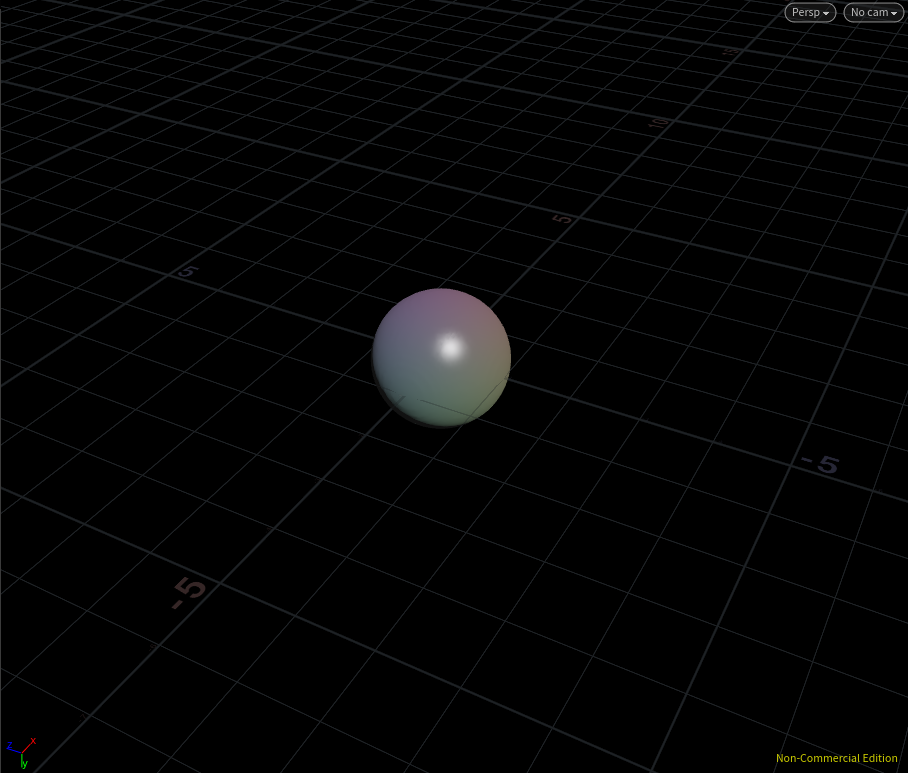
これをメッシュ化すると・・・
(radius=2.5)
(radius=1)
(radius=3.5)
球じゃあまりおもしろくないですね。
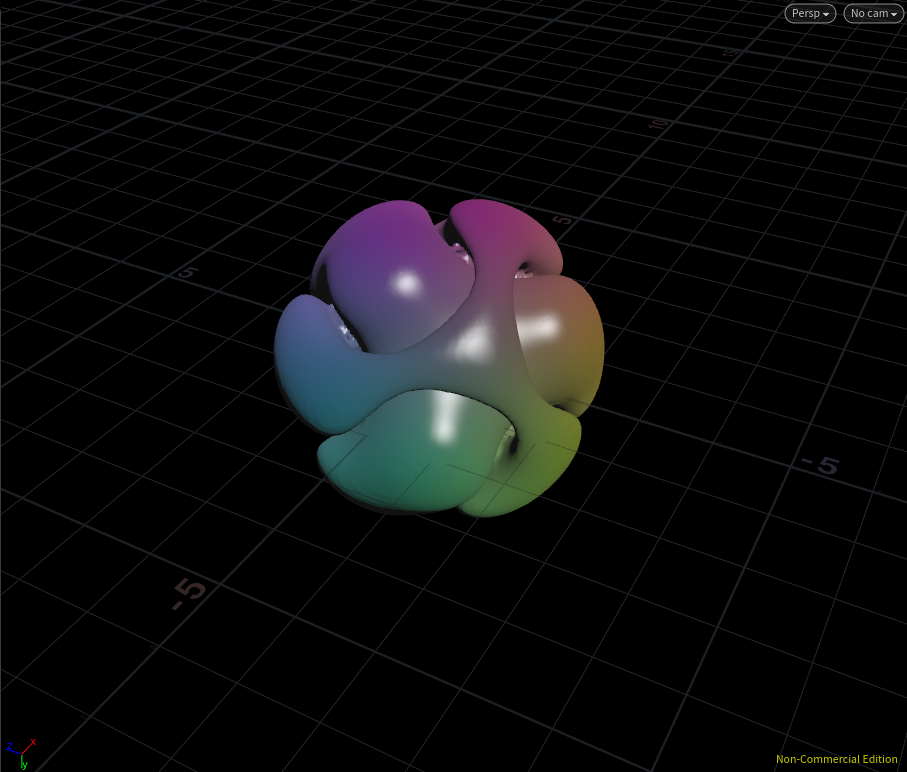
Wonder Tree
同じMetamagicで説明しているWonder Treeと呼んでいる関数は下記のとおり。
Next, try the formula
cos(4.0x/(xx+yy+zz+0.0001))sin(4.0y/(xx+yy+z*z+0.0001))
- cos(4.0y/(xx+yy+zz+0.0001))sin(4.0z/(xx+yy+z*z+0.0001))
- cos(4.0z/(xx+yy+zz+0.0001))sin(4.0x/(xx+yy+z*z+0.0001))
- exp(0.1*(xx+yy+z*z-0.2))
- exp(-10.0*(xx+yy+z*z-0.15))
> inside the bounds -2 to 2.
これをHoudini用に変換すると・・・
``` c
float x = @P.x;
float y = @P.y;
float z = @P.z;
float parm = chf("parm");
float base = cos(parm*x/(x*x+y*y+z*z+0.0001))*sin(parm*y/(x*x+y*y+z*z+0.0001))
+ cos(parm*y/(x*x+y*y+z*z+0.0001))*sin(parm*z/(x*x+y*y+z*z+0.0001))
+ cos(parm*z/(x*x+y*y+z*z+0.0001))*sin(parm*x/(x*x+y*y+z*z+0.0001))
+ exp(0.1*(x*x+y*y+z*z-0.2))
- exp(-10.0 *(x*x+y*y+z*z-0.15));
@density = fit(base,-1,1,1,0);
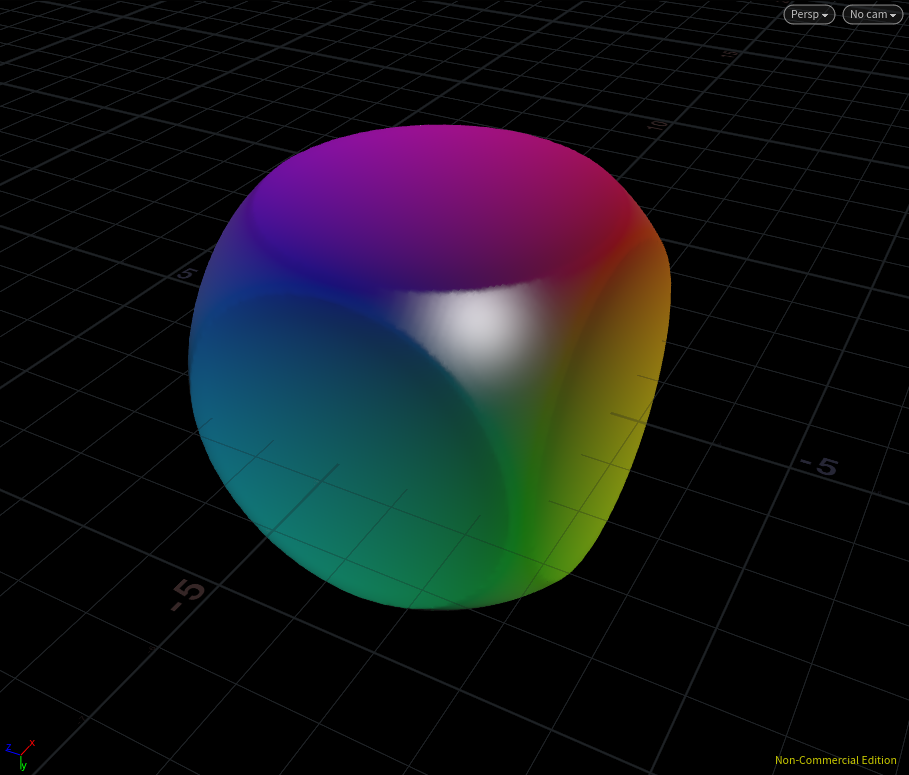
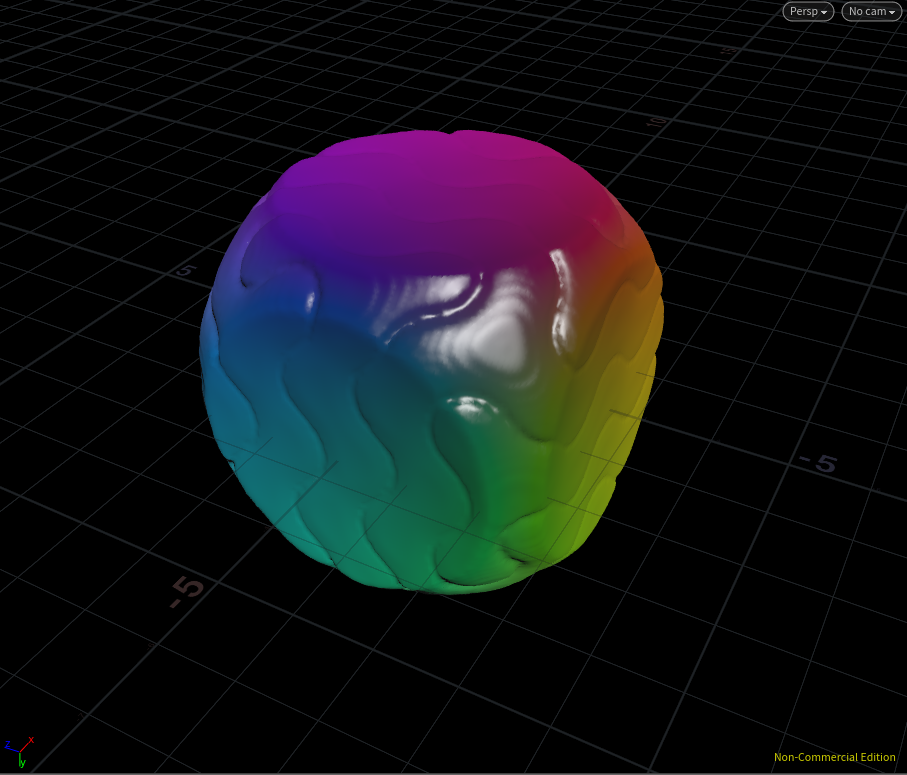
ここではparmというfloatパラメータを作り、模様を変形するのに最適と感じた部分（4.0の部分）をparmで置き換えています。メッシュ化した結果は・・・
(parm=4.0)
(parm=3.16)
(parm=9.0)
気持ち悪い！いい感じ！
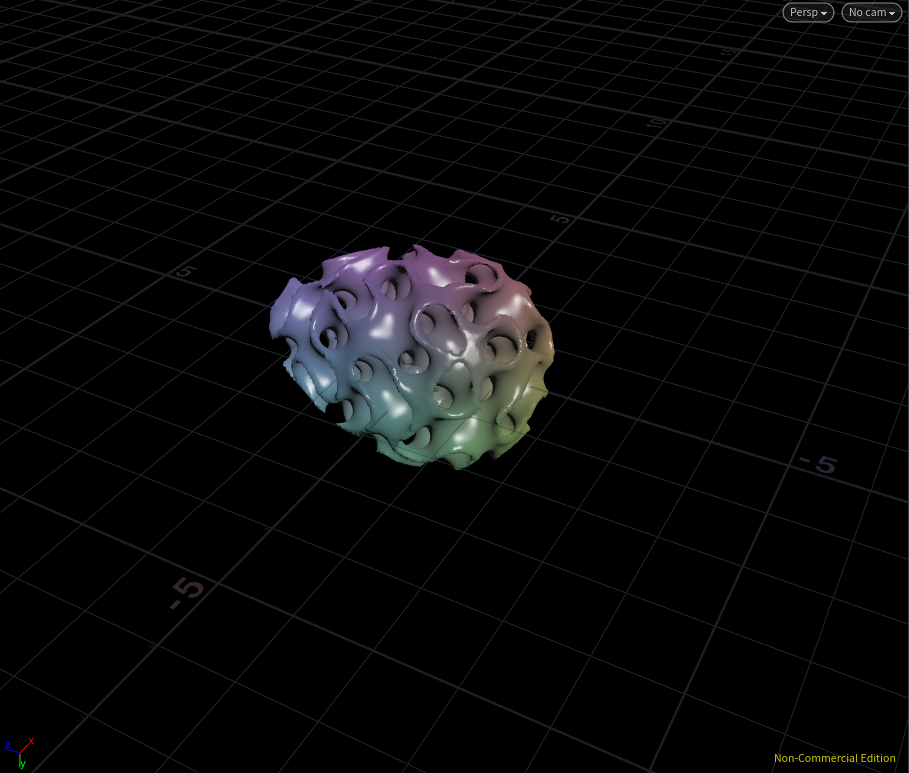
Space Egg
同じMetamagicで説明しているSpace Eggと呼んでいる関数は下記のとおり。
XYZ range: [-8.5, 8.5] x [-8.5, 8.5] x [-17, 17].
-(cos(x) * sin(y) + cos(y) * sin(z) + cos(z) * sin(x))
(cos(x) * sin(y) + cos(y) * sin(z) + cos(z) * sin(x))
+0.05-exp(100.0(xx/64+yy/64 + zz/(1.664)exp(-0.4z/8) - 1))
Houdiniで書くと・・・
``` c
float size = chf("size");
float thickness = chf("thickness");
float x = @P.x*size;
float y = @P.y*size;
float z = @P.z*size;
float base = -(cos(x) * sin(y) + cos(y) * sin(z) + cos(z) * sin(x))
*(cos(x) * sin(y) + cos(y) * sin(z) + cos(z) * sin(x))
+thickness-exp(100.0*(x*x/64+y*y/64 + z*z/(1.6*64)*exp(-0.4*z/8) - 1));
@density = fit(base,-1,1,0,1);
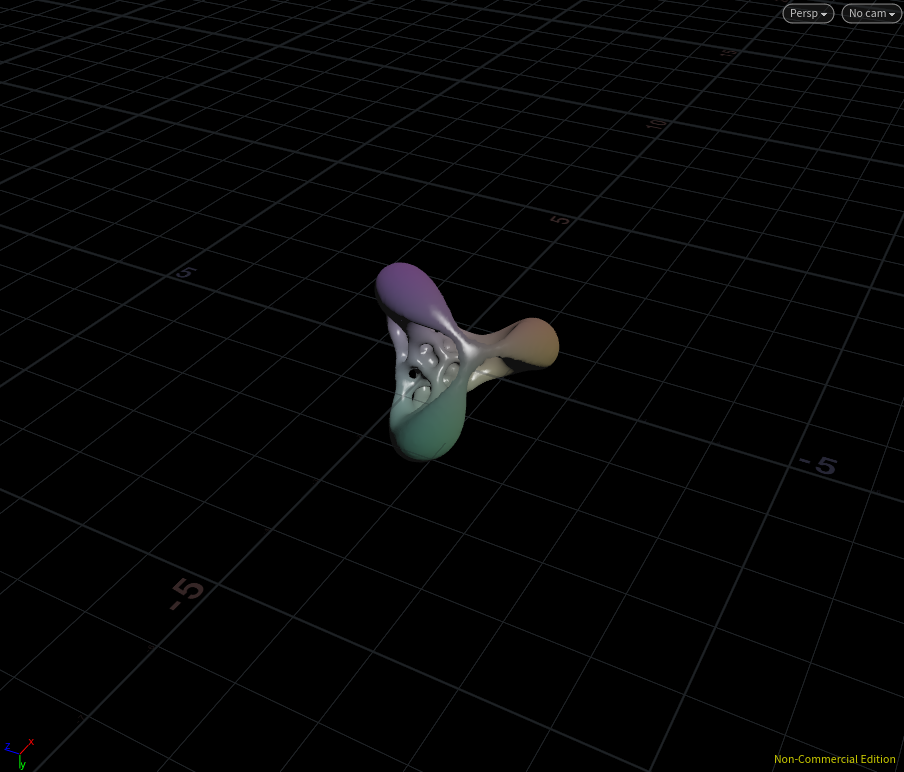
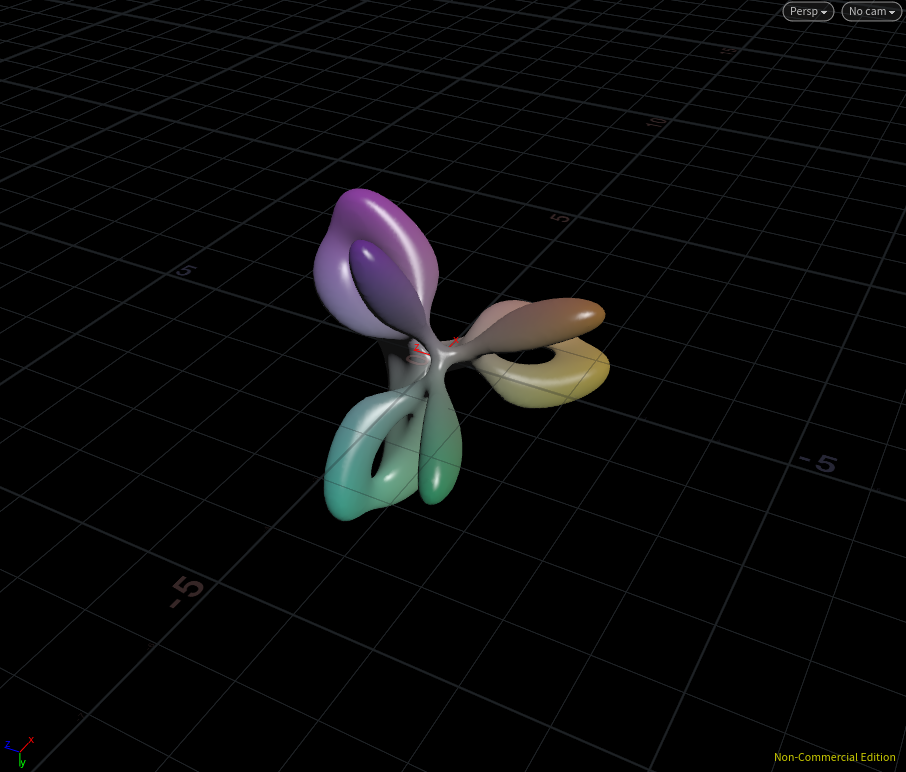
ここではsizeとthicknessという２つのパラメータを設定しています。これをメッシュ化すると・・・
(size=5, thickness=0.2)
(size=1.5, thickness=0.1)
(size=3, thickness=0.8)
エイリアン感あっていい！
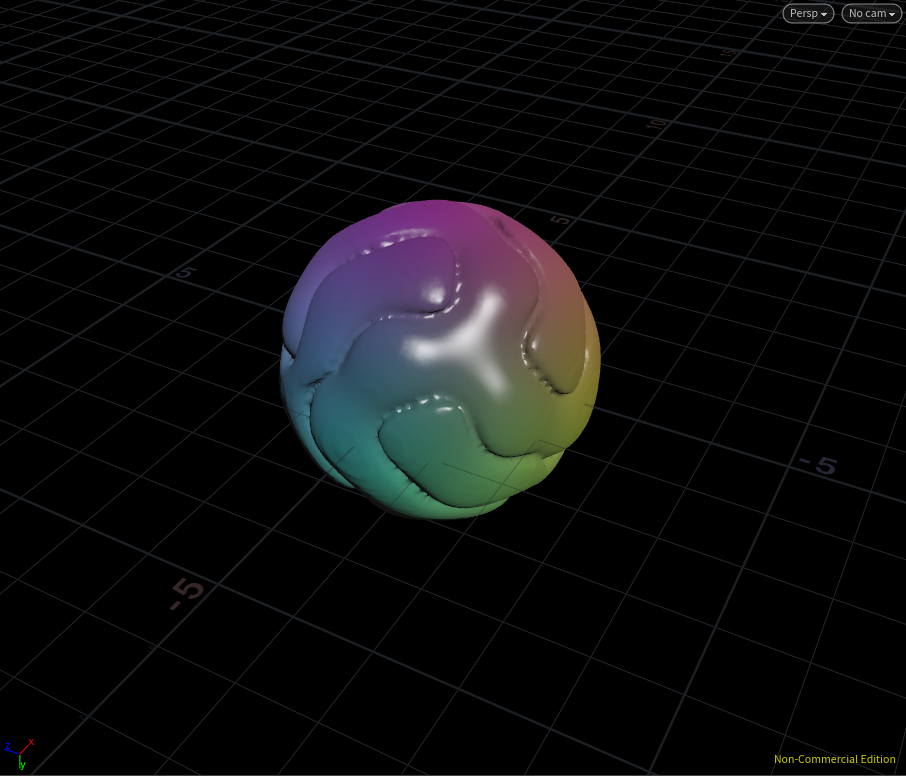
Orbis Gravis
同じMetamagicで説明しているOrbis Gravisと呼んでいる関数は下記のとおり。
XYZ range: [-6, 6] x [-6, 6] x [-6, 6].
-(cos(x) * sin(y) + cos(y) * sin(z) + cos(z) * sin(x))
(cos(x) * sin(y) + cos(y) * sin(z) + cos(z) * sin(x))
+0.02
+exp((xx+yy+zz)-32.0)
Houdiniに翻訳・・・
``` c
float size = chf("size");
float parm = chf("parm");
float x = @P.x*size;
float y = @P.y*size;
float z = @P.z*size;
float base = -(cos(x) * sin(y) + cos(y) * sin(z) + cos(z) * sin(x))
*(cos(x) * sin(y) + cos(y) * sin(z) + cos(z) * sin(x))
+0.02
+exp((x*x+y*y+z*z)-parm);
@density = fit(base,-1,1,1,0);
パラメータとしてサイズをコントロールするsizeと模様を変えるparm（他に言い方思いつかなかった）の二種類を作っています。
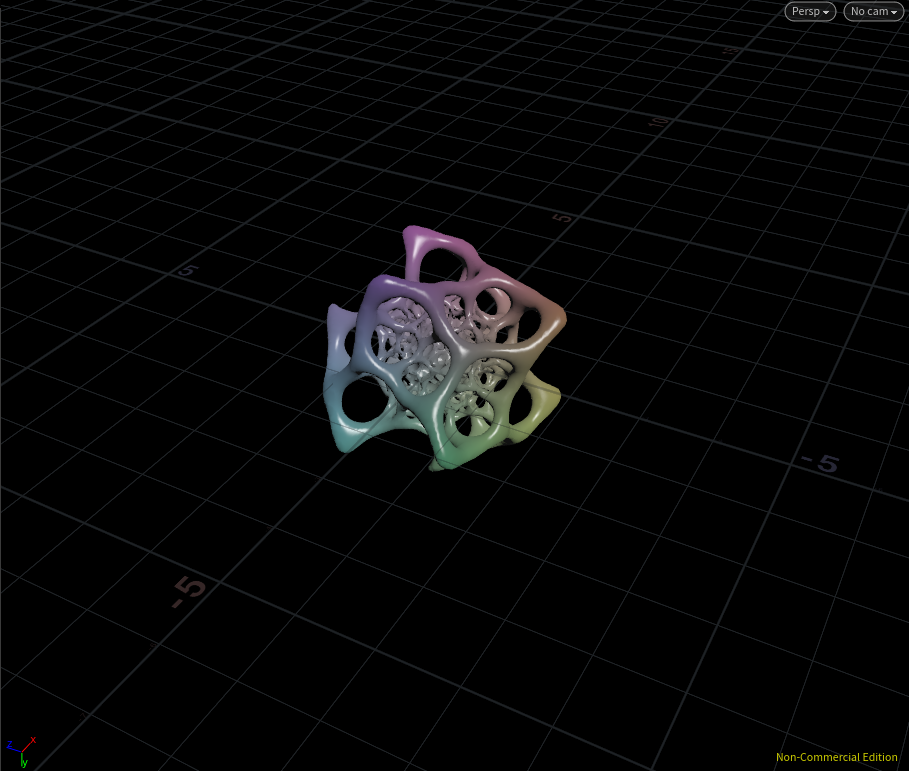
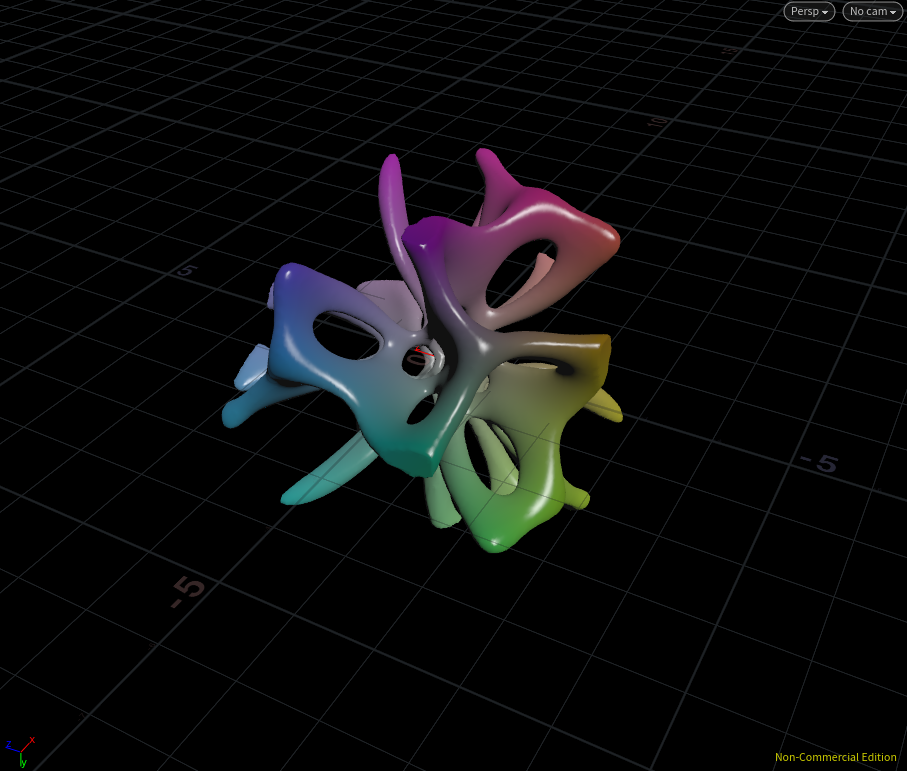
これをメッシュ化すると・・・
(size=2.5, parm=32)
(size=1.5, parm=12)
(size=3, parm=100)
未来球技のボールデザイン！
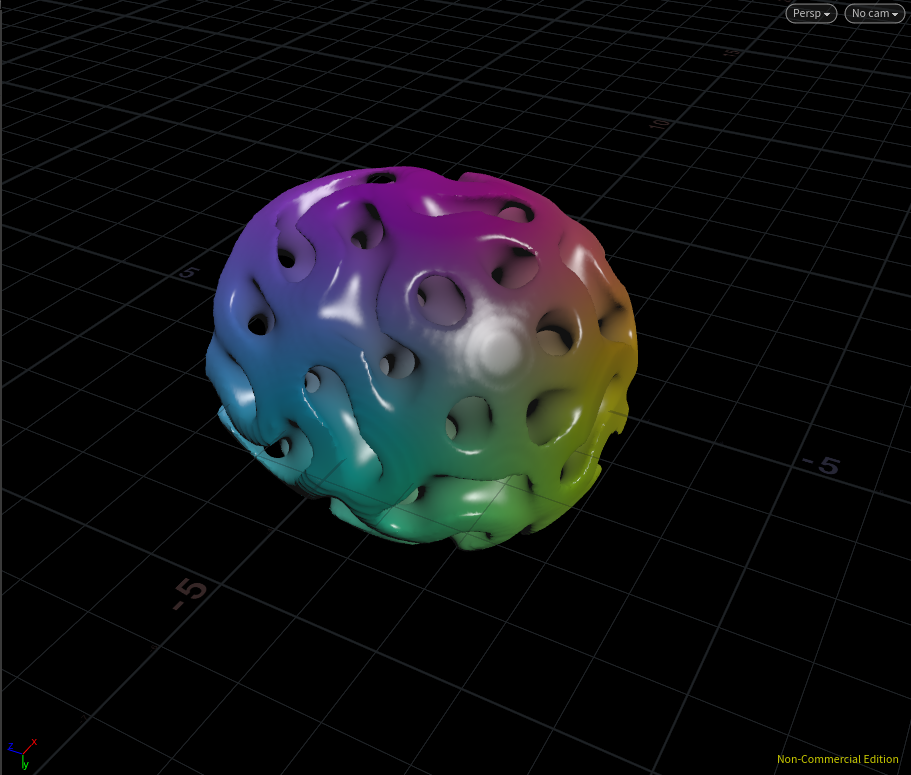
Invader
同じMetamagicで説明しているInvaderと呼んでいる関数は下記のとおり。
XYZ range: [-1, 1] x [-1, 1] x [-1, 1].
cos(4.0x/(xx+yy+zz+0.2)) * sin(4.0y/(xx+yy+zz+0.2))
- cos(4.0y/(xx+yy+zz+0.2)) * sin(4.0z/(xx+yy+zz+0.2))
- cos(4.0z/(xx+yy+zz+0.2)) * sin(4.0x/(xx+yy+zz+0.2))
- exp(0.5*(xx+yy+z*z - 0.1))
Houdiniで書き直すと・・・
``` c
float size = chf("size");
float parm = chf("parm");
float x = @P.x*size;
float y = @P.y*size;
float z = @P.z*size;
float base = cos(parm*x/(x*x+y*y+z*z+0.2)) * sin(parm*y/(x*x+y*y+z*z+0.2))
+ cos(parm*y/(x*x+y*y+z*z+0.2)) * sin(parm*z/(x*x+y*y+z*z+0.2))
+ cos(parm*z/(x*x+y*y+z*z+0.2)) * sin(parm*x/(x*x+y*y+z*z+0.2))
+ exp(0.5*(x*x+y*y+z*z - 0.1));
@density = fit(base,-1,1,1,0);
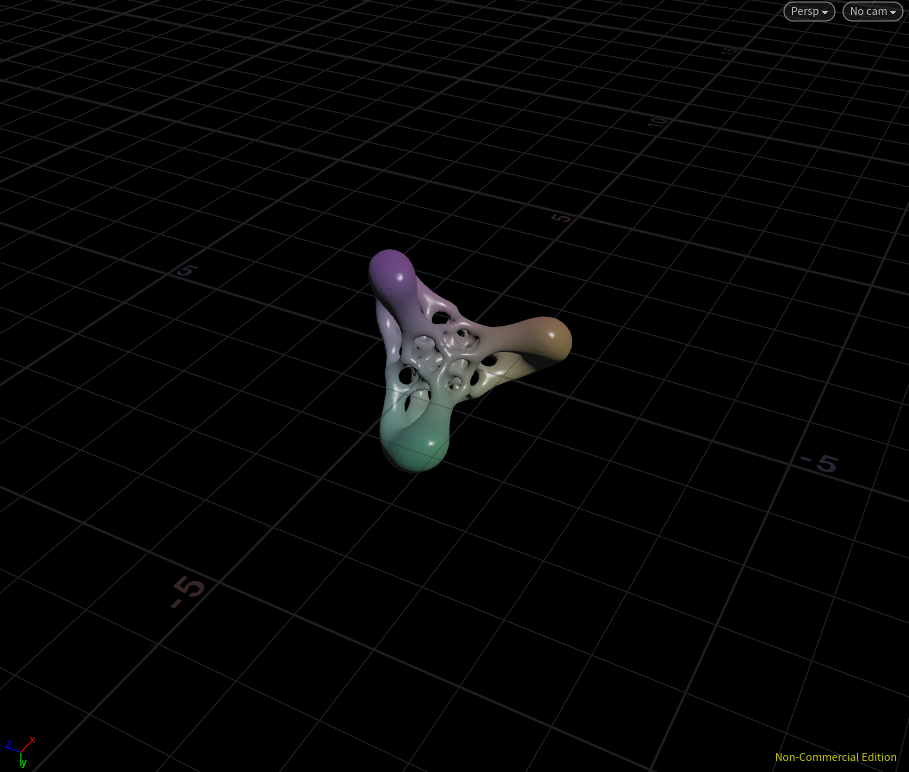
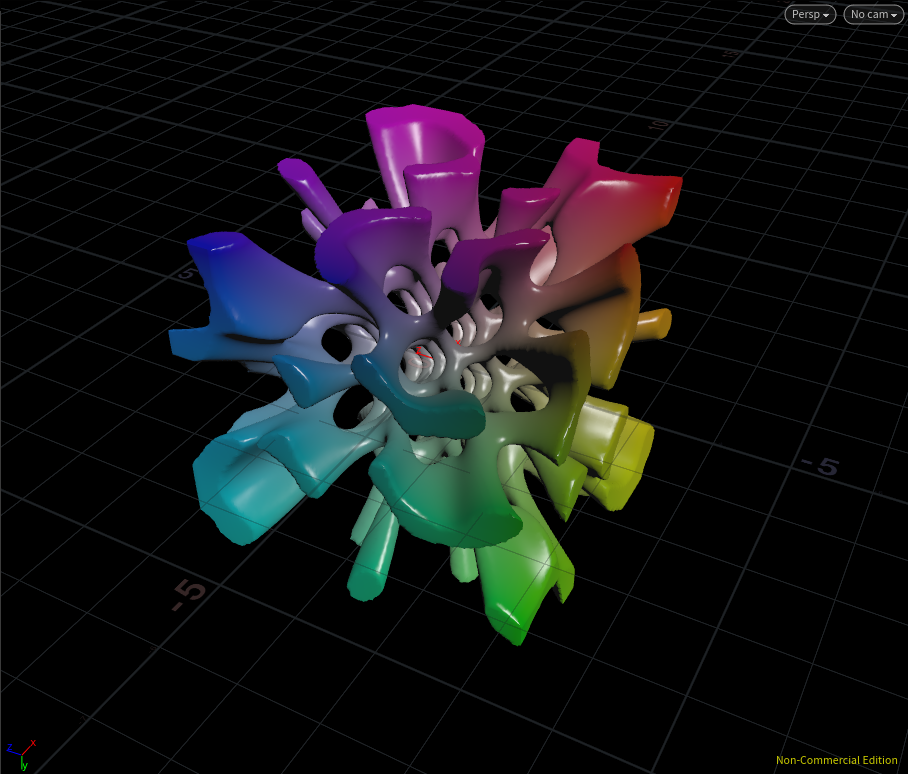
ここでもsize（サイズコントロール）とparm（模様コントロール）という二種類のパラメータを作成しています。パラメータを変えてメッシュ化すると・・・
(size=0.35, parm=4)
(size=0.3, parm=5)
(size=0.15, parm=10)
宇宙に咲く花といった感じ。かっこいい！
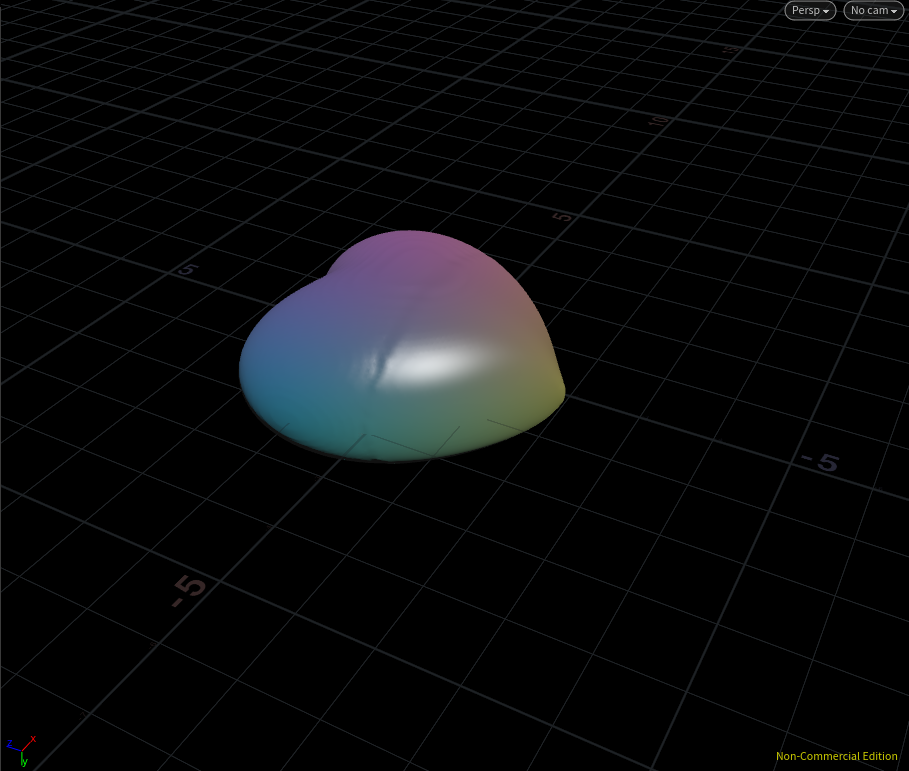
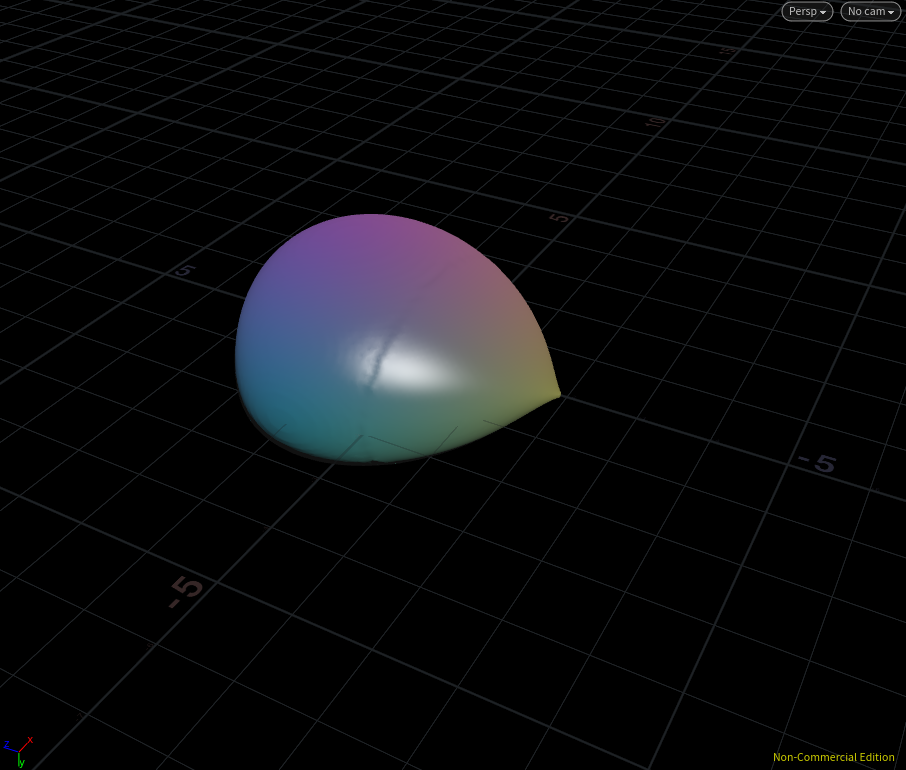
Heart
最後にハートマークを作ります。stackoverflowで解説されていたハートマークを作れる関数は下記のとおり。MATLABを使っているみたいです。
% volume data
step = 0.05;
[X,Y,Z] = meshgrid(-3:step:3, -3:step:3, -3:step:3);
F = (-(X.^2).(Z.^3)-(9/80).(Y.^2).(Z.^3))+((X.^2)+(9/4).(Y.^2)+(Z.^2)-1).^3;
これもHoudiniで書いてみると・・・
``` c
float size = chf("size");
float parm = chf("parm");
float x = @P.x*size;
float y = @P.y*size;
float z = @P.z*size;
float base = (-pow(x,2)*pow(z,3)-(parm/80.0)*pow(y,2)*pow(z,3))+pow((pow(x,2)+(9.0/4.0)*pow(y,2)+pow(z,2)-1),3);
@density = fit(base,-1,1,1,0);
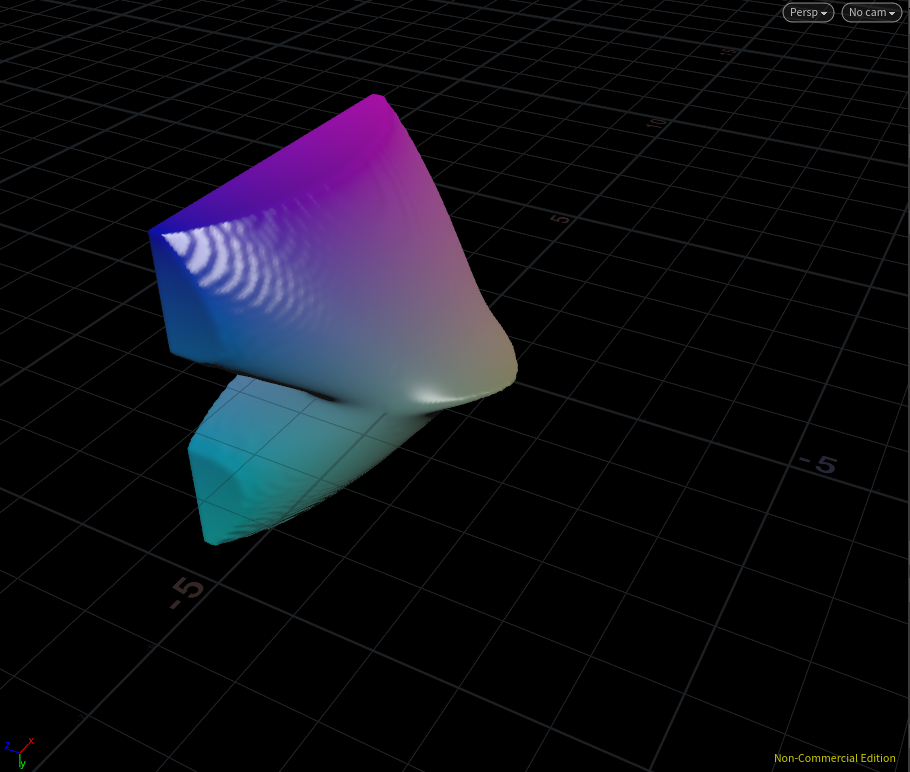
ここでのパラメータはsize（サイズコントロール）とparm（模様のコントロール）。parm=9.0の時にハートの形になります。それ以外だと・・・
(size=0.5, parm=9.0)
(size=0.5, parm=300.0)
(size=0.7, parm=10000.0)
ハートを成長させるとこうなるという見方でみると面白い。
おわりに
以上がHoudiniをツールとして用いて、数理的にIsosurfaceを作る方法となります。
数理的にボクセル空間をいじると簡単に非常に面白い造形ができるということは感じていただけたかと思います。この手法にプラスでマニュアルコントロール（ramp parameterとか、参照点・面との関係性によるコントロール、vdb combine...etc）を加えることでもっと面白い造形が望めると思います。
こんな操作を簡単にできるHoudini、素敵です。
ファイルダウンロード先
データの動作環境:
Houdini Apprentice 16.5.268
ダウンロード先リンク(Github):
https://github.com/jhorikawa/ProgrammingArticleFiles/tree/master/20171210_Algorithmic%20Design%20with%20Houdini%20-%20Isosurface