はじめに
水が5L入る容器と3L入る容器がある、この2つの容器だけを使って、
4Lの水を量るにはどうすれば良いですか?
水はいくらでも使えるものとします。
こちらの問題は、小学生の入学試験から(噂ですが)マイクロソフト社の入社試験まで広く出題されているクイズです。
優秀なエンジニアである読者様は、きっとすぐ答えられると思います。しかしもし「プログラムを書いてこの問題を解きなさい」と言われたら、難易度が一気に跳ね上がると思います。
方法
まずは課題の抽象化
いきなり上記課題をコード化するのは難しいと思います。だったら抽象化しやすい 「容器」 からコーディングしましょう。
課題に出された容器については 「最大容量」、 「水の残量」 と 「空き容量」 3つの属性を有しています(ただし、「空き容量」は「最大容量」-「水の残量」で計算できます)。そして 「満タンにする」 、「空っぽにする」、「他の容器に注ぐ」 3つの操作(メソッド)が取れます。
コードの長さを抑える為に、attr_accessorを使いました。
class Jug
attr_accessor :max, :vol # 最大容量&残量を定義
def initialize(max_capacity)
@max = max_capacity # 最大容量
@vol = 0 # 現在の残量
end
def capacity # 空き容量
@max - @vol
end
def fill # 満タンにする
@vol = @max
end
def empty # 空にする
@vol = 0
end
def pour(jug) # 別の容器に注ぐ
pour_vol = [@vol, jug.capacity].min
jug.vol += pour_vol
@vol -= pour_vol
pour_vol
end
end
正攻法: ユークリッドの互除法で解く
課題を観察すると、容器が大(5L)、小(3L)2種類があり、それぞれを 「Jug_L」 と 「Jug_S」 と書きましょう。
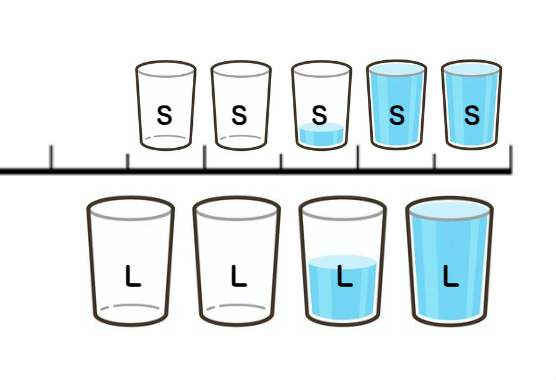
画像のように、ひたすら Jug_S を満タンし、Jug_L に注いでいけば( Jug_L が満タンになった時は空っぽにします。)、その容量の差(最大公約数の倍数)で4Lの水になるはずです。
早速コードを書いてみましょう。
def euclid_algo(s_vol, l_vol, target_vol)
steps = [] # 毎回の行動と結果を記録する
jug_s = Jug.new s_vol # 容器(小)をインスタンス化
jug_l = Jug.new l_vol # 容器(大)をインスタンス化
99.times do |cnt| # 無限ループにならないように、一旦最大99回行動できるように制限する
if jug_s.vol == target_vol || jug_l.vol == target_vol
return steps
end
if jug_s.vol == 0 # 容器(小)が空っぽの時、満タンにする
jug_s.fill
steps << "#{jug_s.max}L容器を満タンにした"
elsif jug_l.capacity == 0 # 容器(大)が満タンになったら、空っぽにする
jug_l.empty
steps << "#{jug_l.max}L容器を空っぽにした"
else
pour_vol = jug_s.pour jug_l # 容器(小)を容器(大)へ注ぐ
steps << "#{jug_s.max}L容器から#{jug_l.max}L容器へ#{pour_vol}Lを注いだ"
end
# 操作の結果を追記
steps[steps.size - 1] += " (#{jug_s.max}L容器: #{jug_s.vol}L, #{jug_l.max}L容器: #{jug_l.vol}L)"
end
nil # 答えが出ない時、nilと返す
end
上記を実行してみると
res = euclid_algo(3, 5, 4)
if res
res.each_with_index do |step, i|
puts "#{i + 1}: #{step}"
end
else
puts "答えが見つからなかった"
end
1: 3L容器を満タンにした (3L容器: 3L, 5L容器: 0L)
2: 3L容器から5L容器へ3Lを注いだ (3L容器: 0L, 5L容器: 3L)
3: 3L容器を満タンにした (3L容器: 3L, 5L容器: 3L)
4: 3L容器から5L容器へ2Lを注いだ (3L容器: 1L, 5L容器: 5L)
5: 5L容器を空っぽにした (3L容器: 1L, 5L容器: 0L)
6: 3L容器から5L容器へ1Lを注いだ (3L容器: 0L, 5L容器: 1L)
7: 3L容器を満タンにした (3L容器: 3L, 5L容器: 1L)
8: 3L容器から5L容器へ3Lを注いだ (3L容器: 0L, 5L容器: 4L)
最適解ではないようですが、一応答え(の一つ)を見つかりました。
2024-01-07更新: 探索木(幅優先探索、反復深化深さ優先探索)で解く
@nodai2h_ITCさんのご指摘通り、「幅優先探索」を使って最短ルートを検索するのは、この部類の課題を解く王道であります。
また、@mogamoga1337さんはJavaScriptでの解き方を投稿くださいましたので、興味のある方は参考して見てください。
変化球: ランダムウォークで解く(非推奨)
2024-01-07更新: ランダムウォークのような機械学習紛いのやり方は、アルゴリズムをうっかり忘れた時だけ使いましょう(笑)
馬鹿正直に水を注いだとしても、最適解には辿り着かないようで、他の方法を探すしかありません。
そこでもう一回課題の内容に注目したいです。
2つの目盛りのない容器しかないですので、できることは以下の6つです。
- 容器(3L)を空にする
- 容器(5L)を空にする
- 容器(3L)を満タンにする
- 容器(5L)を満タンにする
- 容器(3L)を容器(5L)へ水を注ぐ
- 容器(5L)を容器(3L)へ水を注ぐ
この6つの操作の組合せで、最終的に4Lの水をとれば良いとのことです。
だったら、毎回毎回ランダムで一種の操作を選んで実行し、これを何回も繰り返せば、最適解となる組合せにたどり着くはずです。
このような手法はランダムウォーク(Random walk)と言います。日本語では江戸川乱歩ともいいます。一種の確率過程(マルコフ過程)です。
もしモンテカルロ法で円周率とかを求めたことがあれば、理解しやすいでしょう。ちなみに今大人気の機械学習も、この手法の延長線上にあります。
もちろん、今回の場合、状況に応じて実行できない操作も存在しますので、判断条件もつける必要があります。
def random_walk(s_vol, l_vol, target_vol)
steps = [] # 毎回の行動と結果を記録する
jug_s = Jug.new s_vol # 容器(小)をインスタンス化
jug_l = Jug.new l_vol # 容器(大)をインスタンス化
99.times do |cnt| # 無限ループにならないように、一旦最大99回行動できるように制限する
if jug_s.vol == target_vol || jug_l.vol == target_vol
return steps
end
if jug_s.vol == 0 && jug_l.vol == 0 # 容器(小)と容器(大)が空の時
if rand(2) == 0 # ランダムで片方だけ満タンに
jug_s.fill
steps << "#{jug_s.max}L容器を満タンにした"
else
jug_l.fill
steps << "#{jug_l.max}L容器を満タンにした"
end
elsif jug_s.vol == 0 && jug_l.capacity > 0 # 容器(小)が空、容器(大)が満タンでない時
if rand(2) == 0 # ランダムで容器(小)を満タンにするか、容器(大)から注いでもらう
jug_s.fill
steps << "#{jug_s.max}L容器を満タンにした"
else
pour_vol = jug_l.pour jug_s # 容器(大)から容器(小)へ注ぐ
steps << "#{jug_l.max}L容器から#{jug_s.max}L容器へ#{pour_vol}Lを注いだ"
end
elsif jug_s.capacity == 0 && jug_l.capacity == 0 # 容器(小)と容器(大)が満タンの時
if rand(2) == 0 # ランダムで片方だけ空に
jug_s.empty
steps << "#{jug_s.max}L容器を空っぽにした"
else
jug_l.empty
steps << "#{jug_l.max}L容器を空っぽにした"
end
elsif jug_s.capacity == 0 && jug_l.capacity > 0 # 容器(小)が満タンで容器(大)が満タンでない時
if rand(2) == 0 # ランダムで容器(小)を空にするか、容器(大)に注ぐ
jug_s.empty
steps << "#{jug_s.max}L容器を空っぽにした"
else
pour_vol = jug_s.pour jug_l # 容器(小)を容器(大)へ注ぐ
steps << "#{jug_s.max}L容器から#{jug_l.max}L容器へ#{pour_vol}Lを注いだ"
end
elsif jug_l.vol == 0 # 容器(大)が空で容器(小)が空でも満タンでもない時
if rand(2) == 0 # ランダムで容器(大)を空にするか、容器(小)から注いでもらう
jug_l.fill
steps << "#{jug_l.max}L容器を満タンにした"
else
pour_vol = jug_s.pour jug_l # 容器(小)を容器(大)へ注ぐ
steps << "#{jug_s.max}L容器から#{jug_l.max}L容器へ#{pour_vol}Lを注いだ"
end
elsif jug_l.capacity == 0 # 容器(大)が満タンで容器(小)が空でも満タンでもない時
if rand(2) == 0 # ランダムで容器(大)を空にするか、容器(小)に注ぐ
jug_l.empty
steps << "#{jug_l.max}L容器を空っぽにした"
else
pour_vol = jug_l.pour jug_s # 容器(大)から容器(小)へ注ぐ
steps << "#{jug_l.max}L容器から#{jug_s.max}L容器へ#{pour_vol}Lを注いだ"
end
else # 容器(小)と容器(大)両方とも空でも満タンでもない時
if rand(2) == 0 # ランダムで容器(大)を容器(小)に注ぐか、容器(小)を容器(大)に注ぐ
pour_vol = jug_s.pour jug_l # 容器(小)を容器(大)へ注ぐ
steps << "#{jug_s.max}L容器から#{jug_l.max}L容器へ#{pour_vol}Lを注いだ"
else
pour_vol = jug_l.pour jug_s # 容器(大)から容器(小)へ注ぐ
steps << "#{jug_l.max}L容器から#{jug_s.max}L容器へ#{pour_vol}Lを注いだ"
end
end
# 操作の結果を追記
steps[steps.size - 1] += " (#{jug_s.max}L容器: #{jug_s.vol}L, #{jug_l.max}L容器: #{jug_l.vol}L)"
end
nil # 答えが出ない時、nilと返す
end
このようなランダム付きのメソッドを実行する際は、一定の回数で繰り返し実行しないと、最適解までは辿り着けないので(機械学習界隈だと「擬似アニーリング法」と言われているらしい)、一旦1000回実行して、Step数が最も少ない答えをピックアップします。
res_list = []
1000.times do |i| # 1000回テストを行う
res = random_walk(3, 5, 4)
res_list << { res: res, i: i } if res
end
# 結果の表示
if res_list.size > 0
# 回数の最も少ない結果をピックアップ
best_res = res_list.sort_by{ |o| o[:res].size }[0]
puts "== 1000回中の#{best_res[:i]}回目で最適解を獲得した =="
best_res[:res].each_with_index do |step, i|
puts "#{i + 1}: #{step}"
end
else
puts "答えが見つからなかった"
end
約500回のテストで、見事に最適解に辿り着きました:
== 1000回中の475回目で最適解を獲得した ==
1: 5L容器を満タンにした (3L容器: 0L, 5L容器: 5L)
2: 5L容器から3L容器へ3Lを注いだ (3L容器: 3L, 5L容器: 2L)
3: 3L容器を空っぽにした (3L容器: 0L, 5L容器: 2L)
4: 5L容器から3L容器へ2Lを注いだ (3L容器: 2L, 5L容器: 0L)
5: 5L容器を満タンにした (3L容器: 2L, 5L容器: 5L)
6: 5L容器から3L容器へ1Lを注いだ (3L容器: 3L, 5L容器: 4L)
ちなみにこのメソッドはまだ最適化されていません。もし既に試したことのあるStepの組み合わせを飛ばす仕組み(動的計画法)も導入すれば、もっと効率的です(と言っても、ユークリッドの互除法と比べ物にならないほどの計算量が必要です)。
余談: 答えが存在するかを判断
実はこのような水を移し替えパズルは、答えのない組み合わせも沢山あります。
まず当たり前ですが、2つの容器のサイズは必ず異なることです。「5Lの容器2個で4Lの水を汲みなさい」は当然できないです。
そして、汲みたい水は最大の容器の容量より小さいことです。(正確にいうと、容器(大)に容器(小)を足した量まで水を取れますが、容器(大)の容量を超えた時の計算は別のアルゴリズムが必要です)
最後は、上記の条件を満たした時でも、答えが存在しない組み合わせがあります。
例えば、よく出題される(3, 5) => 4、(5, 9) => 7或いは(7, 13) => 5の組み合わせは答えがありますが、(4, 6) => 5や(9, 15) => 10のような組合せは取れません。
その理由は上記ユークリッドの互除法にあります。2つの容器で水を移し替える際、取れる最小単位は2つの容器の最大公約数であります。つまり、2つの容器の最大公約数の倍数の水しか取れないことです。
下記のようなメソッドで判断可能です。
def solvable?(s_vol, l_vol, target_vol)
return false if [s_vol, l_vol].max < target_vol # 容量オーバー判断
target_vol % s_vol.gcd(l_vol) == 0 ? true : false # 最大公約数判断
end
solvable?(3, 5, 4)
=> true
solvable?(2, 6, 4)
=> true
solvable?(4, 6, 5)
=> false
solvable?(9, 15, 10)
=> false
solvable?(1, 2, 5)
=> false