はじめに
みなさんこんにちは。ハーツテクノロジーの James です。この記事は業務の中で得られた知見から書かれています。
この記事の目的は、開発言語別の実行速度と、おおざっぱな行数(ステップ数)を把握するのが目的です。以下の4種類の言語で、同じアルゴリズムを実装し、その実行速度とコード行数を測ります。今回、調べたかった開発言語は以下の5つです。
- C++ / Visual Studio 2019
- C++ / MinGW(v8.1.0)
- Javascript / node.js(v10.16.3)
- C# / Visual Studio 2019
- Python / Python(v3.7.5)
C++, C#, Javascript, Python の実行速度の計測
計測に使うアルゴリズムには「ライプニッツの公式を使って円周率を求める」を選びました。短いコードですが、それなりにCPUを酷使するので目的は達成できると考えています。
結果的に、コードは3パターン作成し、計測しました。
- A, わたし(James)が書いた、小数点以下100桁で計算するコード
- B, 先輩の山崎さんがリファクタリングした、小数点以下20桁で計算するコード
- C, 同僚のOさんが書いたシンプルにdoubleのみで計算するコードをさらに山崎さんがリファクタリングしたコード
どれも、ライプニッツの公式を使って円周率を計算するコードです。
パターンA わたし(James)が書いた、小数点以下100桁で計算するコード
コードの解説
小数点以下100桁までを、1e8 回繰り返し計算します。
小数点以下100桁まで計算のためpi(π)とval(加減する値(1-1/3+1/5-1/7+1/9-⋯))を使います。小数点以下の桁数は設定できます。
- 例)1/3(pi も val と同じ大きさ100桁のint)
| int val[] | [0] | [1] | [2] | [3] | [4] | … | [98] | [99] | [100] |
|---|---|---|---|---|---|---|---|---|---|
| 数 | 0 | 3 | 3 | 3 | 3 | … | 3 | 3 | 3 |
1/3と同じ感じの無限小数をvalで保存して、一度は加算(+)一度は減算(-)と繰り返します。piとvalを加減算と同時に一番後から数の上げと下りを計算します。
- int配列使うの理由
double 型は小数点以下15桁の精度まで計算と表記ができますが、今回はもっと多い桁数を計算して表記したかったので int 配列を作成しました。
コード
A-1. C++(計算時間: VS2019-278.973秒, MinGW-165.098秒)
# include <iostream>
# include <time.h>
# include <cstring>
using namespace std;
# define MAX 101 //小数点以下
int pi[MAX] = { 0 };
int val[MAX] = { 0 };
void val_def(int* q) //calculate val, ‘4/q’を小数点MAXまで計算
{
int start = 4;
for (int i = 0; i < MAX; i++)
{
val[i] = start / *q;
start = (start % *q) * 10;
}
}
void cal() //calculate pi
{
int p = -1, q = 1, num = 1;
while (num <= 1e8) //pi = 4 * (1/1 - 1/3 + 1/5 - ~ 1/(1e8*2-1))
{
val_def(&q);
p *= -1;
for (int i = MAX - 1; i >= 0; i--)
{
if (p == -1 && pi[i] < val[i])//pi[i]-val[i]時val[i]がpiより高い
{
pi[i - 1]--; //piの高桁からpi[i]+10
pi[i] += 10;
pi[i] += p * val[i];
}
else
pi[i] += p * val[i];
if (pi[i] >= 10)//(pi[i] >= 10)時に高桁に数を増加
{
pi[i - 1] += pi[i] / 10;
pi[i] %= 10;
}
}
q += 2;
num++;
memset(val, 0, MAX);
}
}
void print_pi()
{
printf("%d.", pi[0]);
for (int i = 1; i < MAX; i++)
{
printf("%d", pi[i]);
if (i % 10 == 0)
printf(" ");
if (i % 50 == 0)
printf("\n ");
}
}
int main(void)
{
double result = 0;
printf("start\n");
clock_t begin, end;
begin = clock();
cal();
end = clock();
print_pi(); //use if you want to see 0 ~ MAX PI value
result += (double)(end - begin);
printf("\n");
printf(" %f sec(not include print time.)", result / CLOCKS_PER_SEC);
}
A-2. C#(計算時間: 458.992秒)
using System;
namespace leibniz
{
class func
{
static int MAX = 101; //小数点以下 100まで
int[] pi = new int[MAX];
int[] val = new int[MAX];
public void val_def(int q)
{
int start = 4;
for (int i = 0; i < MAX; i++)
{
val[i] = start / q;
start = (start % q) * 10;
}
}
public void cal()
{
int p = -1, q = 1, num = 1;
while (num <= 1e8) //pi = 4 * (1/1 - 1/3 + 1/5 - ~ 1/(1e8*2-1))
{
val_def(q);
p *= -1;
for (int i = MAX - 1; i >= 0; i--)
{
if (p == -1 && pi[i] < val[i])
{
pi[i - 1]--;
pi[i] += 10;
pi[i] += p * val[i];
}
else
pi[i] += p * val[i];
if (pi[i] >= 10)
{
pi[i - 1] += pi[i] / 10;
pi[i] %= 10;
}
}
q += 2;
num++;
Array.Clear(val, 0, MAX);
}
}
public void print()
{
Console.Write(pi[0] + ".");
for (int i = 1; i < MAX; i++)
{
Console.Write(pi[i]);
if (i % 10 == 0)
Console.Write(" ");
if (i % 50 == 0)
Console.Write("\n ");
}
}
}
class Program
{
static void Main(string[] args)
{
double result = 0;
DateTime begin, end;
begin = DateTime.Now;
func _func = new func();
_func.cal();
end = DateTime.Now;
result += end.Subtract(begin).TotalSeconds;
_func.print(); //use if you want to see 0 ~ MAX PI value
Console.WriteLine("\n " + end.Subtract(begin).TotalSeconds + " sec");
}
}
}
A-3. JavaScript(計算時間: 456.066秒)
let MAX = 101; ////小数点以下 100まで
let pi = Array.apply(null,new Array(MAX)).map(Number.prototype.valueOf,0);
let val = Array.apply(null,new Array(MAX)).map(Number.prototype.valueOf,0);
let begin = new Date().getTime();
let result = 0;
function val_def(q){
let start = 4;
for (let i = 0; i < MAX; i++){
val[i] = Math.floor(start / q);
start = (start % q) * 10;
}
}
function cal(){
let p = -1, q = 1, num = 1;
while (num <= 1e8) { //pi = 4 * (1/1 - 1/3 + 1/5 - ~ 1/(1e8*2-1))
val_def(q);
p *= -1;
for (let i = MAX - 1; i >= 0; i--){
if (p == -1 && pi[i] < val[i]) {
pi[i - 1]--;
pi[i] += 10;
pi[i] += p * val[i];
}
else
pi[i] += p * val[i];
if (pi[i] >= 10) {
pi[i - 1] += parseInt(pi[i] / 10);
pi[i] %= 10;
}
}
q += 2;
num++;
val = [];
}
}
function print(){
process.stdout.write(`${pi[0]}.`);
for (let i = 1; i < MAX; i++){
process.stdout.write(`${pi[i]}`);
if (i % 10 == 0)
process.stdout.write(" ");
if (i % 50 == 0)
process.stdout.write("\n ");
}
}
cal();
let end = new Date().getTime();
print(); //use if you want to see 0 ~ MAX PI value
result = (end-begin)/1000;
console.log(`\n${(end-begin)/1000} sec`);
A-4. Python(計算時間: 1148.174秒)
import time
MAX = 11 #遅いため小数点以下 10まで
pi = [0] * MAX
val = [0] * MAX
def cal():
global pi
global val
p = -1
q = 1
num = 1
while num <= 1e8: #pi = 4 * (1/1 - 1/3 + 1/5 - ~ 1/(1e8*2-1))
val_def(q)
val = list(reversed(val))
p *= -1
for index,i in enumerate(pi):
if p == -1 and pi[index] < val[index]:
pi[index + 1] -= 1
pi[index] += 10
pi[index] += p * val[index]
else:
pi[index] += p * val[index]
if i >= 10:
pi[index + 1] += pi[index] // 10
pi[index] %= 10
q += 2
num += 1
val = [0] * MAX
pi = list(reversed(pi));
def val_def(q):
global val
start = 4
for index,i in enumerate(val):
val[index] = start // q
start = (start % q)*10
def print_pi():
global pi
print("%d." % pi[0],end="")
for index,i in enumerate(pi):
if index == 0:
continue
print(i,end="");
if (index % 10) == 0:
print(" ",end="")
if (index % 50) == 0:
print(" ")
print("")
if __name__ == '__main__':
print("start")
begin = time.time()
cal()
end = time.time()
print_pi()
print(end - begin," sec")
パターンB, 先輩の「山崎さん」がリファクタリングした、小数点以下20桁で計算するコード
コードの解説
小数点以下20桁までを、分母が 1e9 になるまで繰り返し計算します。
コード
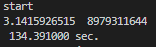
B-1. C++(計算時間: VS2019-216.595秒, MinGW-134.391秒)
# include <stdio.h> // printf()
# include <time.h> // clock()
# define MAX 21 //小数点以下 20桁
int pi[MAX] = { 0 };
void pi_add( long long _q, int _a=1 )
{
long long start = 4; // _q は 1e9 まで来る想定なので long 32bit では足りない
for ( int i=0; i<MAX; i++ )
{
pi[i] += (start / _q) * _a;
start = (start % _q) * 10;
}
}
int main()
{
printf( "start\n" );
auto begin = clock(); // 実行時間を計測
for ( long long q=1; q<=1e9 ; ) // pi = 4/1 - 4/3 + 4/5 - 4/7 + ... 4/1e9
{
pi_add( q ); // 加算
q += 2;
pi_add( q, -1 ); // 減算
q += 2;
}
// 計算のあと、各桁を 0 - 9 の範囲に調整する
for ( int i=MAX-1; i>0; i-- ) // 0以下の値は、上の桁から拝借してくる
{
for ( ; pi[i] < 0 ; ) {
pi[i-1] -= 1;
pi[i] += 10;
}
}
for ( int i=MAX-1; i>0; i-- ) // 10以上の値は、上の桁に送る
{
if ( pi[i] >= 10 ) {
pi[i-1] += pi[i] / 10 ;
pi[i] %= 10 ;
}
}
// 表示
printf( "%d.", pi[0]);
for ( int i = 1; i < MAX; i++)
{
printf( "%d", pi[i] );
if ( i % 10 == 0 ) printf( " " );
}
printf( "\n" );
printf( " %f sec.", (double)(clock() - begin) / CLOCKS_PER_SEC ); // 実行時間を表示
return 0 ;
}
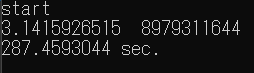
B-2. C#(計算時間: 287.459秒)
using System;
namespace leibniz
{
class Program
{
static int MAX = 21;
static int[] pi = new int[MAX];
static void pi_add(long _q, int _a = 1)
{
long start = 4;
for (int i = 0; i < MAX; i++)
{
pi[i] += (int)(start / _q) * _a;
start = (start % _q) * 10;
}
}
static void Main(string[] args)
{
Console.WriteLine("start");
DateTime begin = DateTime.Now;
for (long q = 1; q <= 1e9;)// pi = 4/1 - 4/3 + 4/5 - 4/7 + ... 4/1e9
{
pi_add(q);
q += 2;
pi_add(q, -1);
q += 2;
}
for (int i = MAX - 1; i > 0; i--) // 0以下の値は、上の桁から拝借してくる
{
for (; pi[i] < 0;)
{
pi[i - 1] -= 1;
pi[i] += 10;
}
}
for (int i = MAX - 1; i > 0; i--) // 10以上の値は、上の桁に送る
{
if (pi[i] >= 10)
{
pi[i - 1] += pi[i] / 10;
pi[i] %= 10;
}
}
Console.Write(pi[0] + ".");
for (int i = 1; i < MAX; i++)
{
Console.Write(pi[i]);
if (i % 10 == 0)
Console.Write(" ");
if (i % 50 == 0)
Console.Write("\n ");
}
Console.WriteLine("\n{0} sec.", DateTime.Now.Subtract(begin).TotalMilliseconds / 1000); //時間表示
}
}
}
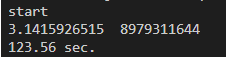
B-3. JavaScript(計算時間: 123.56秒)
console.log( 'start' )
const begin = Date.now() // 実行時間を計測
const MAX = 21 // 小数点以下 20桁
var pi = Array( MAX ).fill( 0 )
function pi_add( _q, _a=1 ) // 加算
{
let start = 4
for ( let i=0; i<MAX; i++ )
{
pi[i] += Math.floor( start / _q ) * _a
start = ( start % _q ) * 10
}
}
for ( let q=1; q<=1e9 ; ) // pi = 4/1 - 4/3 + 4/5 - 4/7 + ... 4/1e9
{
pi_add( q ) // 加算
q += 2
pi_add( q, -1 ) // 減算
q += 2
}
// 計算のあと、各桁を 0 - 9 の範囲に調整する
for ( let i=MAX-1; i>0; i-- ) // 0以下の値は、上の桁から拝借してくる
{
for ( ; pi[i] < 0 ; )
{
pi[i-1] -= 1
pi[i] += 10
}
}
for ( let i=MAX-1; i>0; i-- ) // 10以上の値は、上の桁に送る
{
if ( pi[i] >= 10 ) {
pi[i-1] += parseInt( pi[i] / 10 )
pi[i] %= 10
}
}
// 表示
var r = `${pi[0]}.`
for ( let i=1; i<MAX; i++ )
{
r += `${pi[i]}` + ( (i % 10 == 0) ? ' ' : '' )
}
console.log( r )
console.log( `${ ( Date.now() - begin ) / 1000 } sec.` ) // 実行時間を表示
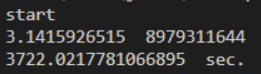
B-4. Python(計算時間: 3722.021秒)
import time
print( "start" )
begin = time.time() # 実行時間を計測
MAX = 21 # 小数点以下 20桁
pi = [0] * MAX
def pi_add( q, a=1 ):
start = 4
for i in range( 0, MAX ) :
pi[i] += start // q * a
start = (start % q) * 10
q = 1
while q <= 1e9: # pi = 4/1 - 4/3 + 4/5 - 4/7 + ... 4/1e9
pi_add( q ) # 加算
q += 2
pi_add( q, -1 ) # 減算
q += 2
# 計算のあと、各桁を 0 - 9 の範囲に調整する
for i in range( MAX-1, 0, -1 ) : # 0以下の値は、上の桁から拝借してくる
while pi[i] < 0 :
pi[i-1] -= 1
pi[i] += 10
for i in range( MAX-1, 0, -1 ) : # 10以上の値は、上の桁に送る
if pi[i] >= 10 :
pi[i-1] += pi[i] // 10
pi[i] %= 10
# 表示
print( "%d." % pi[0], end="" )
for i in range( 1, MAX ) :
print( pi[i], end="" )
if ( i % 10 ) == 0 :
print( " ", end="" )
print( "" )
print( time.time() - begin, " sec." ) # 実行時間を表示
パターンC, 同僚の「Oさん」が書いたシンプルにdoubleのみで計算するコードをさらに山崎さんがリファクタリングしたコード
3回(小数点以下double(15)まで、1e9まで計算)
コード
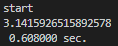
C-1. C++(計算時間: VS2019-2.6秒, MinGW-0.608秒)
# include <stdio.h> // printf()
# include <time.h> // clock()
int main()
{
printf( "start\n" );
auto begin = clock(); // 実行時間を計測
double l = 0.0;
for ( double n=1; n<1e9; ) // l = 1/1 - 1/3 + 1/5 - 1/7 + ... 1/1e9
{
l += 1.0 / n ;
n += 2 ;
l -= 1.0 / n ;
n += 2 ;
}
printf( "%1.16f\n", l * 4 );
printf( " %f sec.", (double)(clock() - begin) / CLOCKS_PER_SEC ); // 実行時間を表示
return 0;
}
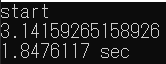
C-2. C#(計算時間: 1.847秒)
using System;
namespace Leibniz
{
class Program
{
public static void Main()
{
System.Console.WriteLine("start");
System.DateTime begin = System.DateTime.Now; // 実行時間を計測
double l = 0.0;
for (double n = 1; n < 1e9;) // l = 1/1 - 1/3 + 1/5 - 1/7 + ... 1/1e9
{
l += 1.0 / n;
n += 2;
l -= 1.0 / n;
n += 2;
}
System.Console.WriteLine(l * 4);
System.Console.WriteLine("{0} sec", System.DateTime.Now.Subtract(begin).TotalMilliseconds / 1000);
}
}
}
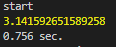
C-3. JavaScript(計算時間: 0.756秒)
console.log( 'start' )
const begin = Date.now() // 実行時間を計測
var l = 0.0
for ( let n=1; n<1e9; ) // l = 1/1 - 1/3 + 1/5 - 1/7 + ... 1/1e9
{
l += 1.0 / n
n += 2
l -= 1.0 / n
n += 2
}
console.log( l * 4 )
console.log( `${ ( Date.now() - begin ) / 1000 } sec.` ) // 実行時間を表示
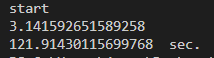
C-4. Python(計算時間: 121.914秒)
import time
print( "start" )
begin = time.time() # 実行時間を計測
l = 0.0
n = 1
while n<1e9 : # l = 1/1 - 1/3 + 1/5 - 1/7 + ... 1/1e9
l += 1.0 / n
n += 2
l -= 1.0 / n
n += 2
print( l * 4 )
print( time.time() - begin, " sec." ) # 実行時間を表示
結果
実行環境
- CPU : Intel Core i7-7500U 2.70GHZ
- RAM : 8 GB
- SSD : 250 GB
- OS : Windows 10 Pro
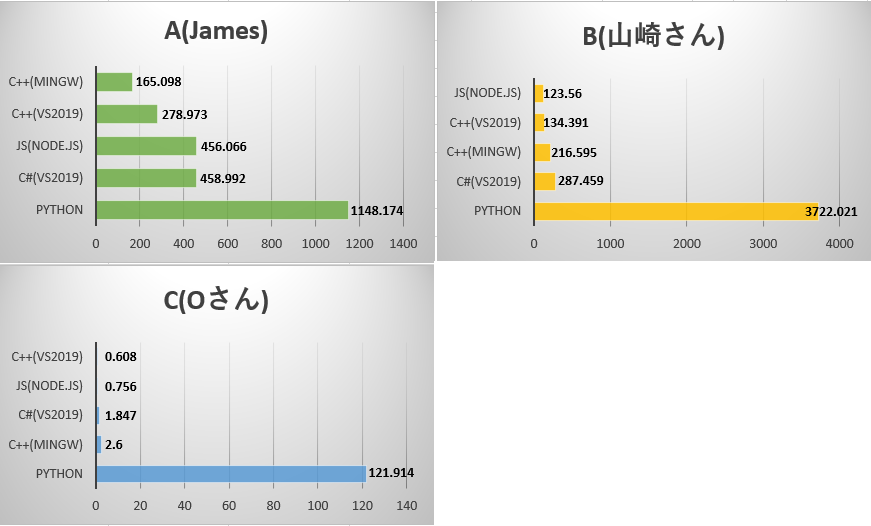
実行速度(秒)
| code | VS2019/C++ | MinGW/C++ | node.js/Javascript | VS2019/C# | Python |
|---|---|---|---|---|---|
| A | 278.973 | 165.098 | 456.066 | 458.992 | 1148.174 |
| B | 216.595 | 134.391 | 123.56 | 287.459 | 3722.021 |
| C | 2.6 | 0.608 | 0.756 | 1.847 | 121.914 |
やはり C++ がよい成績を出しました。でも、2番目に Javascript が速いです。これは予想外。。。Python は3位のC#より3倍以上、最大で約100倍遅いです。
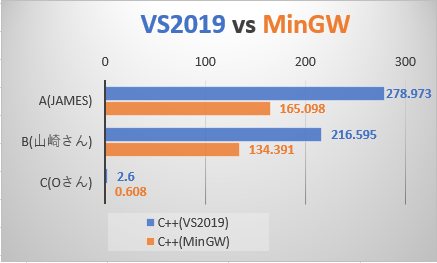
追加で、MinGW と Visual Studio の速度の違いも意味があると思います。どちらも「O2」最適化オプションで計測しました。
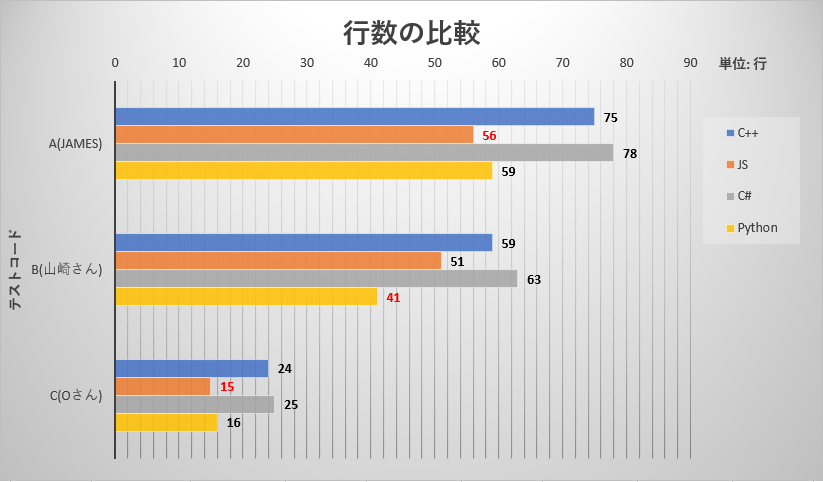
コード量(行数)
コード量はコメント業も空白行も含む純粋な行数です。好みの書き方に左右されるので、あくまでも参考値です。
| code | C++ | Javascript| C# | Python |
|:---:|---:|---:|---:|---:|---:|
| A | 75 | 56 | 78 | 59 |
| B | 59 | 51 | 63 | 41 |
| C | 24 | 15 | 25 | 16 |
コード量は C++, C# が長めで Python, Javascript 短めに思います。
3つとも Javascript と Python は長さ面で似ていましたが、速度面では反対の感じに結果がでました。
総評
この計測の前に g++(C++ compiler) で「-O2」オプションを使わずに計測しました。その計測のときにはJavascriptが速度面で1位でした。
でも最適化オプション「-O2」を使ったあとで結果が変わりました。
しかし速度だけでなくコード量を一緒に見れば Javascript が合理的な言語だと思いました。
追加テスト
ABC、3つの中で1つ(B,山崎さんのコード)だけ Javascriptが速い結果が出ました。それもなぜJavascriptが速いかが解決してないので簡単なテストをしました。
ループの速度が違うのでループを1回は1e5反復,2回は1e6反復して5回1e9までテストしました。(オプションで -O2使う)
ループ速度
コード
- C++
# include <iostream>
# include <time.h>
int main(void)
{
int i = 0;
double val = 1e5; //ループ 回数
while (i < 5)
{
double a = 0;//これのtypeを変える
int j = 0;
double result = 0.0;
while(j < 5)
{
a = 0;
auto begin = clock();
for (int q = 1; q <= val; q++)//これのtypeを変える
{
a++;
}
result += clock() - begin;
j++;
}
printf("long long q ~ 10^%d, double a = %10.0f: %.3f sec \n", i + 5, a, (result / 5) / CLOCKS_PER_SEC);
i++;
val *= 10; //ループ 回数増加(i=0:1e5, i=1:1e6, i=2:1e7, i=3:1e8, i=4:1e9)
}
return 0;
}
| MinGW(double a) | MinGW(int a) |
|---|---|
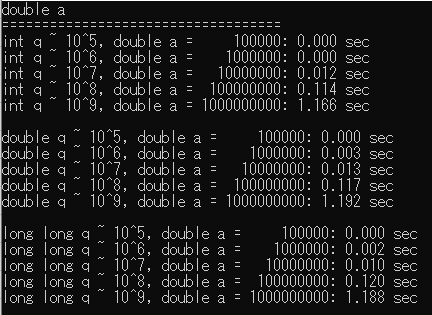 |
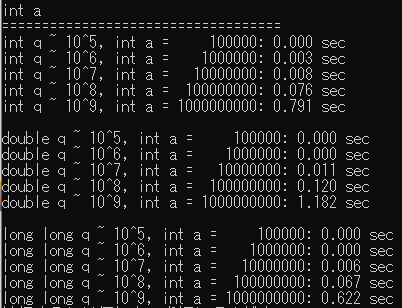 |
| VS2019(double a) | VS2019(int a) |
|---|---|
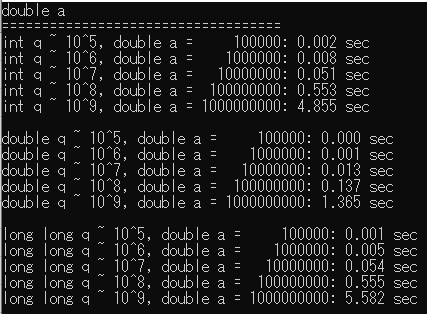 |
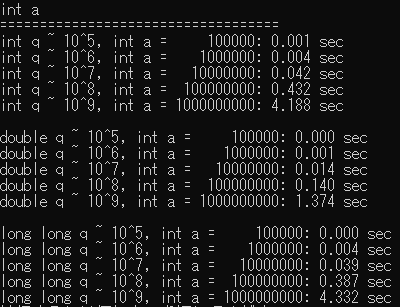 |
- Javascript
let i = 0
let val = 1e5 //ループ 回数
while (i < 5)
{
let a = 0
let j = 0
let result = 0.0
while (j < 5)
{
a = 0;
let begin = Date.now()
for (let q = 1; q <= val; q++)
{
a++
}
result += Date.now() - begin
j++
}
console.log(`10^${i+5}: ${((result/5) / 1000).toFixed(3)} sec, a = ${a}`)
i++
val *= 10 //ループ 回数増加(i=0:1e5, i=1:1e6, i=2:1e7, i=3:1e8, i=4:1e9)
}
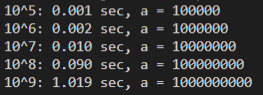
結果
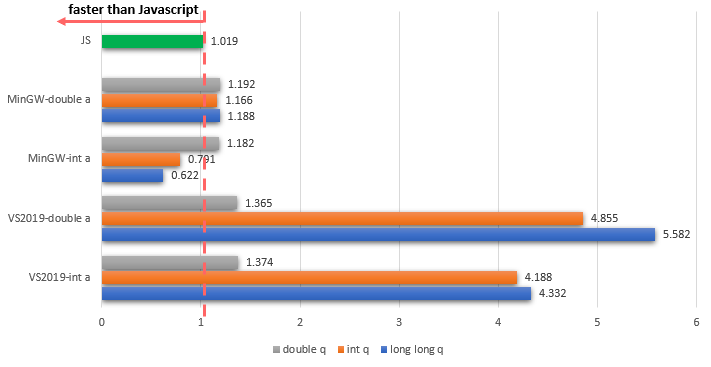
10^9反復する場合だけ結果を整理します。(単位: 秒)
| int q | double q | long long q | |
|---|---|---|---|
| MinGW - int a | 0.791 | 1.182 | 0.622 |
| MinGW - double a | 1.166 | 1.192 | 1.188 |
| VS2019 - int a | 4.188 | 1.374 | 4.332 |
| VS2019 - double a | 4.855 | 1.365 | 5.582 |
| Javascript - type関係ない | 1.019 | - | - |
総合的にVS2019はループカウント(q)のデータタイプがdouble時には一番速かったけどそれも10^7からはJavascriptより遅くなりました。
でもMinGWはdoubleを使う時だけ(aかqかは関係ない)10^7からJavascriptより遅くなりましたが、doubleを使用しない時(aとq全体)にはJavascriptより全体の場合で速くなりました。
VS2019がループカウント(q)をdoubleで使う時だけMinGWと同じ実行時間が出ましたが、intとlong longを使う時にはVS2019がMinGWより3~4倍ぐらい遅くなりました。
まとめ
まだ結果について明快な解答がありません。でも個人的にJavascriptが結構いい言語ということを知りました。
このあと Python がどこまで発展するかまだわからないが、今は速度が必要で、資金など資源が不足ぎみなら C++ より Javascript を使うのもいいと思いました。
みなさまのご意見もお聞かせください。よろしくお願いいたします。